非平衡异方差单向分类模型中的广义置信区间
许利可, 范永辉
(天津师范大学 数学科学学院, 天津 300387)
非平衡异方差单向分类模型中的广义置信区间
许利可*, 范永辉
(天津师范大学 数学科学学院, 天津 300387)
讨论了在单向分类模型中多个正态总体样本容量不等, 方差不等时样本均值的同时广义置信区间的估计问题. 结合Scheffe 和Bonferroni 区间的定义, 给出了相应的广义检验变量及广义枢轴量, 进而求得样本均值的同时广义置信区间, 并且通过数据模拟, 和文献[1]中给出的方法比较, 本文所给方法具有较好的可行性.
广义枢轴量; 广义置信区间; 单向分类模型

H0:μ1=μ2= …=μa↔
H1:μ1,μ2, … ,μa不全相等.
(1)
如果否定了H0, 我们会继续考虑某些总体期望两两之间的差异性, 即考虑一些μi-μj(i 本文考虑在多个正态总体下样本容量不等且方差不等时正态均值的同时置信区间的估计问题, 并在广义检验变量, 广义枢轴量, 广义置信区间定义的基础之上, 结合王松桂[2]给出的Scheffe和Bonferroni区间的定义及构造方法, 给出了类似方法构造的广义检验变量和广义枢轴量, 进而解得样本均值的同时广义置信区间.并且通过数据模拟容易看出, 由Scheffe区间的定义构造的广义枢轴量找出的置信域的覆盖率接近预先给定的值, 并具有较好的稳定性. 由Bonferroni区间的定义构造的广义枢轴量找出的置信区间在覆盖率和区间长度上都明显优于文献[1]中给出的方法, 因此具有较好的可行性. 首先介绍广义p值, 广义检验变量和广义枢轴量的概念. 设X为一组随机变量,x是X的观测值,θ是我们感兴趣的参数,η是冗余参数, 且η可为参数向量. 假设要检验的问题是 H0:θ≤θ0↔H1:θ>θ0, (2) 其中θ0为预先给定的值. 定义1(广义检验变量[10]). 设T(X,x,θ,η) 为随X机变量,X的观测值x, 以及参数(θ,η)的函数. 若T满足 1)T(X,x,θ0,η) 的分布与冗余参数无关; 2)T(X,x,θ,η) 的观测值T(x,x,θ,η) 与未知参数无关; 3) 对固定的x和η,T(X,x,θ,η)的分布关于θ随机单调增或随机单调减. 则称T(X,x,θ,η) 为一个广义检验变量. 当T(X,x,θ,η)的分布关于θ随机单调增时, 对于检验问题(1)定义广义p值为 p=Pr(T(X,x,θ,η)≥T(x,x,θ,η)|θ=θ0). 当T(X,x,θ,η)的分布关于θ随机单调减时, 对于检验问题(1)定义广义p值为 p=Pr(T(X,x,θ,η)≤T(x,x,θ,η)|θ=θ0). 对于给定显著性水平α, 如果p<α, 则拒绝原假设, 反之接受. 定义2(广义枢轴量[11]). 设R(X,x,θ,η)为随机变量X,X的观测值x, 及参数(θ,η)的函数. 若R满足 1)R(X,x,θ,η)的分布与未知参数无关; 2)R(X,x,θ,η)的观测值R(x,x,θ,η)与冗余参数无关. 则称R(X,x,θ,η)为一个广义枢轴量. 广义置信区间可以利用R(X,x,θ,η)来构造. 对给定一个置信水平1-α, 如果有样本空间的一个子集Cα,满足Pr(R∈Cα)=α,则称Θc(α)={θ∈Θ|R(x,x,θ,η)∈Cα}为θ的置信系数为1-α的广义置信区间. 更多关于广义检验变量和广义置信区间的内容可参见Tusi和Weerahandi[10]和Weerahandi[11]. 考虑非平衡异方差单向分类模型: i=1, …,a,j=1, …,ni. (3) 对于该模型, 我们首先考虑的是假设检验问题(1). 若拒绝了H0, 即我们会进一步考虑不同的μi之间的差异情况, 一般是考虑μi-μj(i≠j) 的置信区间. 在模型(3)中, 令 (i=1, …,a), (4) 则易知 (i=1, …,a), (5) 对于假设检验问题(1), 本节结合王松桂[2]给出的Scheffe区间的定义及构造方法, 给出针对于检验问题(1)的广义检验变量, 并且如果否定了H0, 继续考虑样本总体期望两两之间的差异性, 即考虑一些μi-μj(i 沿用上一节的估计及记号, 令 (6) 下面先给出广义检验变量, 定义 (7) 3) 对于固定的y,σ2,T11关于Hμ随机单调增. 因而(7)式定义的T11是广义检验变量. 因为μ和零向量差异越多,T11越倾向于取比较大的值, 所以广义p值为:p=P(T11>t11). 对于给定的显著性水平α, 当p<α时拒绝检验(1)的原假设, 即认为Hμ≠0. 记ei是第i个分量为1, 其余分量全为0的列向量,i=1, 2, …,a. 对任意i≠j,μi-μj=(ei-ej)′μ. 因ei-ej∈M(H′), 考虑所有的l′μ,l∈M(H′)的同时置信区间.先给出如下引理. 引理1设α,β均为n×1 的向量,A为n×n的正定方阵, 则 (8) 引理易从Cauchy-Schwardz不等式(α′β)2≤(α′A-1α)(β′Aβ) 推出. 下面构造广义枢轴量, 定义 (9) 因而(9)式定义的T12是广义枢轴量, 可由此来构造μi-μj(i (10) 故对于β′Hμ, 它的置信系数为1-γ的同时置信区间为 (11) 假设Φ=H1μ=(h′1μ, …,h′mμ)′为m个线性无关的可估函数, 其中rk(H1)=m, 现要求m个可估函数h′iμ,i=1, …,m的同时置信区间, 对每一个h′iμ作置信系数为1-γ的置信区间Ii, 这样虽然每个Ii包含h′iμ的概率是1-γ, 但h′iμ∈Ii,i=1, …,m的同时成立的概率(即置信系数)却不再是1-γ, 一般比1-γ较小. 现设Ei,i=1, …,m为m个随机事件,P(Ei)=1-γ,i=1, …,m. 则根据Bonferroni不等式: (12) 易得P(h′iμ∈Ii,i=1,…,m)≥1-mγ. 当m较大时, 这个概率的下界可以很小, 为克服这一缺陷, 把求h′iμ置信系数为1-γ的置信区间Ii, 改为求h′iμ置信系数为1-γ/m的置信区间Ii, 从而每个Ii包含h′iμ的概率提高到了1-γ/m. 一般地, 把用这种方法求得可估函数的同时置信区间称为Bonferroni 区间. Weerahandi[10]已经给出了关于两样本均值的广义检验变量, 现在根据Weerahandi[11]给出如下广义枢轴量: (13) (14) (15) 则(15)式的分布与下面的式子相同 (16) 由上述易知: 1)Tkl的分布与未知参数无关; 因而(13)式定义的Tkl是广义枢轴量, 可由此来构造检验μk-μl的广义置信区间, 其中k≠l. 本节将对检验问题(1), 首先考虑检验问题(1)的变形, 即H0:Hμ=0vsH1:Hμ≠0, 且当Hμ≠0成立时, 结合广义枢轴量T12, 考虑Hμ的置信域, 给出Hμ广义置信域覆盖率的模拟结果; 其次结合广义枢轴量Tkl(k,l=1, 2, …,a且k≠l), 得出μk-μl广义置信区间长度及其覆盖率的模拟结果. 模拟方法: 2) 然后进行3 000次内循环, 每次生成3个正态分布样本和一组自由度分别为ni的卡方分布样本, 根据以上生成的样本和(9)式, 计算出一组T12的值, 然后找出T12的1-γ/2分位点, 从而得到Hμ的一个置信域, 将此置信域记为Θc1; 3) 最后根据第2步找出的Hμ的一个置信域Θc1, 统计第1步中由观测值t12计算出的Hμ落在Θc1中的频数, 计算出广义置信域的覆盖率. 表1 基于Scheffe区间定义构造出的Hμ的广义置信域的覆盖率 表2, 表3分别给出了由文中基于Bonferroni区间的定义构造的广义枢轴量Tkl和文献[1] 中方法计算出的μk-μl(k,l=1, 2, …,a且k≠l) 的置信系数分别为0.9和0.95的置信区间长度lkl及其覆盖率的模拟结果, 这里不妨把文献[1] 中方法称为F法,即对于两个均值不等方差相等的独立正态样本, 结合F分布的一些性质, 构造出的针对于两样本均值和方差的F分布, 然后利用F检验法求两正态样本均值差相等性的检验方法. 表2 基于Bonferroni方法和F法得出的μk-μl置信系数为0.9广义置信区间长度及覆盖率 表3 基于Bonferroni方法和F法得出的μk-μl置信系数为0.95广义置信区间长度及覆盖率 模拟方法: 2) 然后做4 000次内循环, 根据以上生成的样本和(16)式, 计算出一组Tkl的值, 然后找出Tkl的γ/2分位点和1-γ/2分位点, 从而得到μk-μl的一个广义置信区间, 将此广义置信区间记为Θc2; 本文研究了在单向分类模型中多个正态总体样本容量不等, 方差不等时样本均值相等性检验问题.并在样本均值不等时, 给出了广义检验变量及广义枢轴量, 并通过所给出的广义枢轴量, 模拟出样本均值的同时广义置信区间及其覆盖率. 由模拟结果可以看出, 根据Scheffe区间的定义构造的广义枢轴量找出的Hμ广义置信域的覆盖率接近预先给定的值, 且具有较好的稳定性; 根据Bonferroni 区间的定义构造的广义枢轴量找出的μk-μl(k,l=1, 2, …,a且k≠l)的同时广义置信区间的覆盖率接近由Bonferroni 方法确定的区间覆盖率, 并且通过与文献[1]中方法计算出的区间长度比较, 很容易看出基于Bonferroni 方法确定的区间长度远小于文献[1]中方法计算出的区间长度, 而由文献[1]构造出置信区间的覆盖率虽然接近预先给定的值, 但从总体的区间覆盖率来说远低于预先给定的值. 综上说明了本文所提供的方法很好的解决了求多个正态总体样本均值的同时置信区间问题. [1] 高 峰, 郭 云. 正态总体均值的F检验法[J].淮阴工学院学报, 2005,14(5): 6-7. [2] 王松桂, 史建红, 尹素菊, 等. 线性模型引论[M].北京: 科学出版社, 2004. [3] 梅长林, 范金城. 数据分析方法[M].北京: 高等教育出版社, 2006. [4] 茆诗松, 王静龙, 濮晓龙. 高等数理统计[M].北京: 高等教育出版社, 2006. [5] WELCH B L. The significance of the difference between two means when the population variances are unequal[J].Biometrika, 1938,29(3): 350-362. [6] 宋立新. 一类Behrens-Fisher检验问题的解法[J].汕头大学学报(自然科学版), 2013,28(3): 36-39. [7] 徐礼文, 梅 波. Behrens-Fisher问题的参数Bootstrap检验[J].统计与决策, 2015(10): 23-27. [8] GAMAGE J K. Generalized p-values and the multivariate Behrens-Fisher problem[J]. Linear Algebra & Its Applications, 1997,253(1): 369-377. [9] 许家清. Behrens-Fisher 问题的广义置信区间[J].统计与决策, 2011(2): 29-30. [10] TSUI K W, WEERAHANDI S. Generalized p-Values in significance testing of hypotheses in the presence of nuisance parameters[J]. Journal of the American Statistical Association, 1989,84(406): 602-607. [11] WEERAHANDI S. Generalized confidence intervals[J]. Journal of the American Statistical Association, 1993,88(423):899-905. [12] KRISHNAMOORTHY K, LU Y. Inferences on the common mean of several normal populations based on the generalized variable method[J]. Biometrics, 2003,59(2): 237-247. [13] CHANG C H, PAL N. Testing on the common mean of several normal distributions[J]. Computational Statistics & Date Analysis, 2008,53(2): 321-333. [14] 王 琰, 李树有, 宓 颖. 多个正态总体均值相等性检验方法的模拟比较[J].东北师大学报(自然科学版), 2012,44(4): 10-15. Thegeneralizedconfidenceregionsintheone-wayclassificationmodelofunbalancedheteroscedasticity XU Like, FAN Yonghui (College of Mathematical Science, Tianjin Normal University, Tianjin 300387, China) The paper discusses the simultaneous generalized confidence regions of means estimation of multiple normal populations which means and variances are all different. With the definition of Scheffe and Bonferroni intervals, the paper gives the relevant generalized test variable and generalized pivotal quantity and acquires the simultaneous generalized confidence regions of population means, and through the date simulation and compared with the methods given in literature[1],the method given in this paper is good feasible. generalized pivotal quantity; generalized confidence regions; one-way classification model 2017-06-27. 国家自然科学基金项目(41272245). *E-mail: 1660469349@qq.com. 10.19603/j.cnki.1000-1190.2017.06.004 1000-1190(2017)06-0747-07 O212.1 A
1 预备知识
2 问题简介

3 正态总体均值的相等性检验和置信区间
3.1 基于Scheffe方法的广义检验及同时置信区间


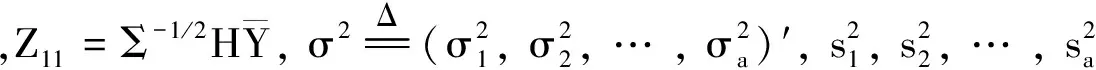
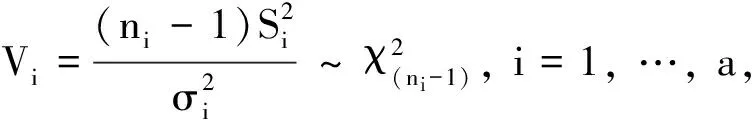


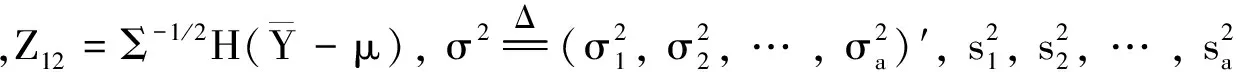
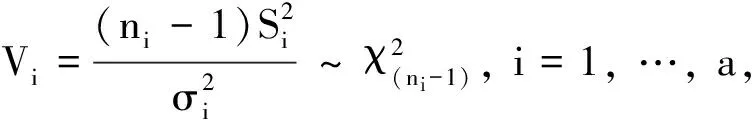




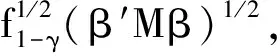

3.2 基于Bonferroni方法的广义置信区间




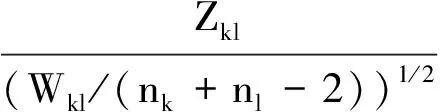


4 模拟结果和模拟方法
4.1 基于Scheffe区间的定义构造出广义置信域的模拟结果



4.2 基于Bonferroni方法构造的广义置信区间的模拟结果





5 总结

