浅埋矩形顶管求解的复变函数实践

李新源，刘国彬

(同济大学 土木工程学院，上海 200092)

浅埋矩形顶管求解的复变函数实践

李新源，刘国彬

(同济大学 土木工程学院，上海 200092)

同时考虑洞周边界与地表边界，采用复变函数法求解浅埋矩形顶管施工引起的土体应力场、位移场。根据黎曼存在定理、复变函数的三角插值理论，提出计算含矩形的半无限域到同心圆环域共形映射的计算方法。在此基础上，将边界条件等式两边都展成洛朗级数，采用幂级数解法求得了复应力函数的系数。从该解法与有限元解的对比来看，在大部分点处结果相差不大，误差在2%左右。结果表明：(1)提出的保角映射函数形式及系数的求解方法适用于浅埋矩形隧洞；(2)提出的复变函数解法具有步骤清晰、收敛快、操作简单等特点。

半无限体；矩形顶管；复变函数；幂级数法

随着社会的发展，城市建设活动中的顶管工程也越来越多。现已有许多方法来求解顶管施工引起的土体附加应力场、位移场[1]。Verruijt[2]首先将复变函数法用于求解浅埋圆形隧洞开挖问题；Strack[3]得到了隧洞受浮力作用时的解；童磊[4]给出了隧道任意变形下围岩的应力场、位移场的解答；江学良等[5]给出了地面集中荷载作用下浅埋圆形洞室的应力解答；Lu等[6]得到了地表荷载及围岩自重作用下浅埋圆形隧洞围岩的应力场。虽然已有许多浅埋隧洞开挖问题的复变函数解法，但目前都仅限于浅埋圆形隧洞，浅埋矩形隧洞开挖问题的复变函数解法鲜见文献报道。本文提出了含矩形隧洞的半无限域到同心圆环域保角映射函数的形式，对浅埋矩形隧洞开挖问题进行了求解，为掌握隧洞应力分布，指导隧洞设计、施工提供了依据。

1 问题的描述

假设围岩为线弹性体并在开挖前已沉降稳定，不考虑重力作用时浅埋矩形隧洞开挖问题可简化为如图1所示平面应变问题，图中地平线边界Γ1为零应力边界，隧洞边界Γ2为已知位移边界，h为隧洞中心埋深，θ为隧洞边界上点的幅角。隧洞周围岩体的应力场、位移场是由Γ2的位移引起的。

设σij、ui(i，j=1，2)为图1中围岩在直角坐标系下的应力、位移分量，则他们可用两个复应力函数φ(z)、ψ(z)表示为[2，7]

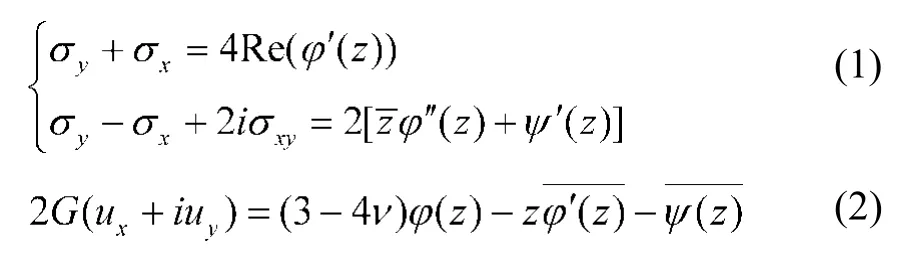
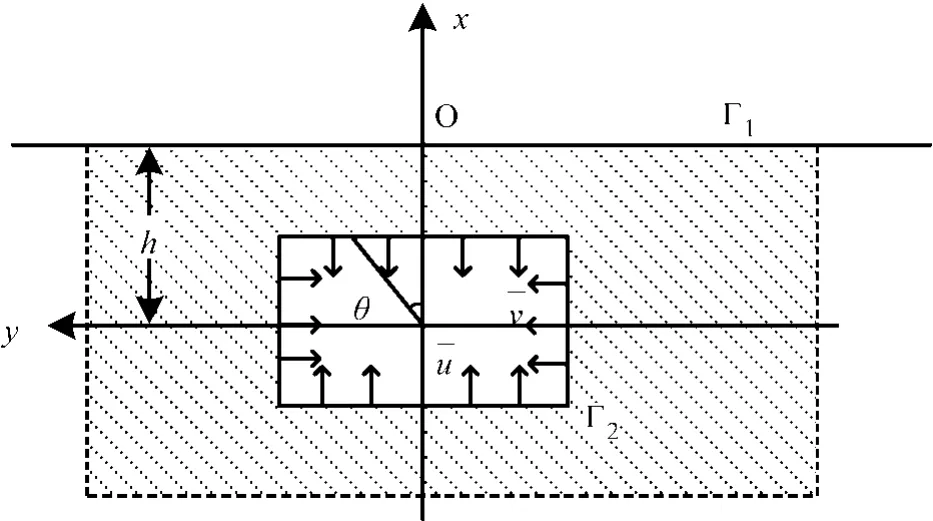
图1 浅埋矩形隧洞开挖问题Fig.1 Shallow cavern with rectangular excavation crosssection

其中，φ(z)、ψ(z)的表达式可根据图1的边界条件式(1)、(2)求得：

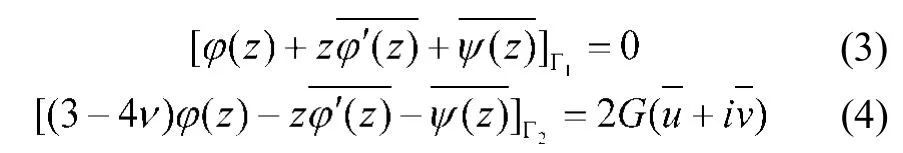
2 共形映射函数

映射函数的求取是采用复变函数求解的第一步。本文所求的映射函数应能将图1中的D映射为图2中的同心圆环域D′。基于前人研究，作者提出了此映射函数的形式：

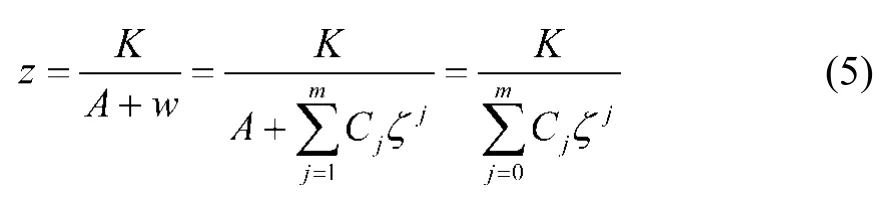
式中：K、A、Ci均为系数。系数可采用“两步走”求解步骤，其具体过程如下：

(1)采用恰当的映射函数z=z(w)将z平面的半无限域D映射为w平面上的域D'。

(2)在第一步映射的基础上，采用特定的映射函数w=w(ζ )将w平面上的外边界Γ'1映射为ζ平面上的单位圆环Γ''1。

根据Schinzinger[8]的研究成果，可将A选为0.3，且根据ρ=K/2h=0.3来选取K的值，之后根据边界对应条件来求取Ci与r的值。

3 复应力函数求解过程

由于φ(ζ )、ψ(ζ )可以展开成洛朗级数的形式：

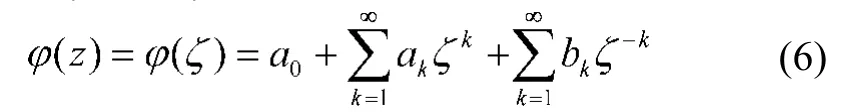
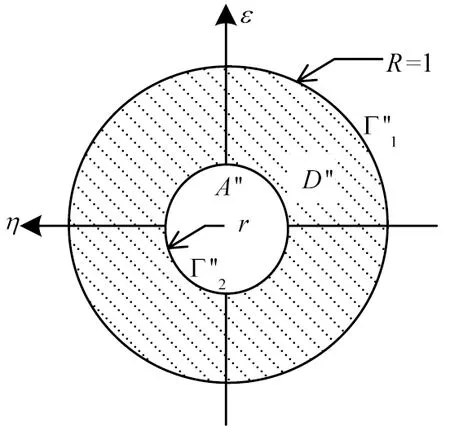
图2 保角映射后的图形Fig.2 The region after conformal mapping

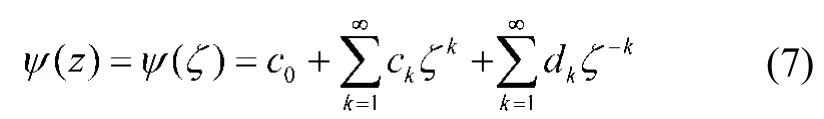
因此问题最终归结为根据边界条件求解ak、bk、ck、dk的值。设ζ =ρσ，其中σ =eiα，α为ζ平面上边界点的幅角。对于地表边界ζ =rσ，由式(5)得

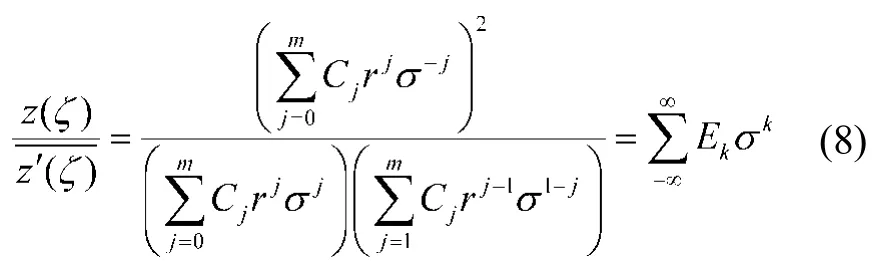
在实际计算时，设Ek的项数为s，当k＞s时，Ek、E-k均为0。Ek的值可根据式(8)左右两侧σ同幂次系数相等来求得。

式(3)中x=h边界条件可表示为

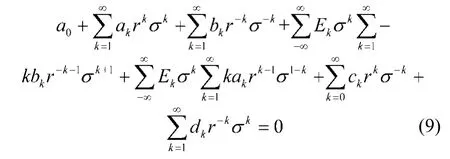
比较上式等号左右两边σ的同幂次系数可得一组求解ak、bk、ck、dk的方程

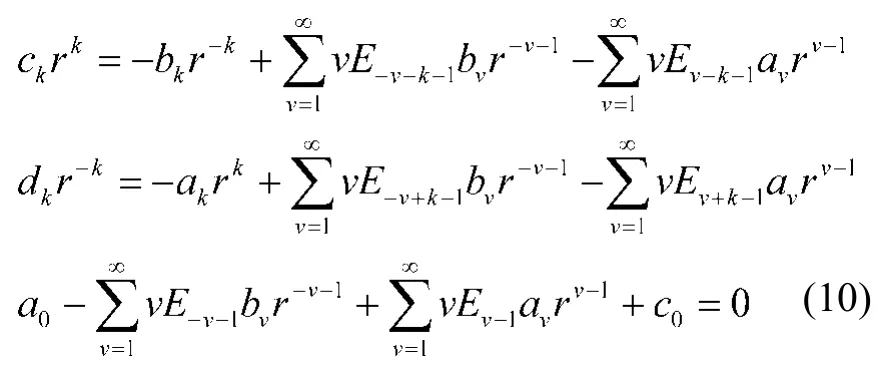
考虑洞口边界条件，将得到另一组求解方程。(4)式中隧洞边界条件可表示为

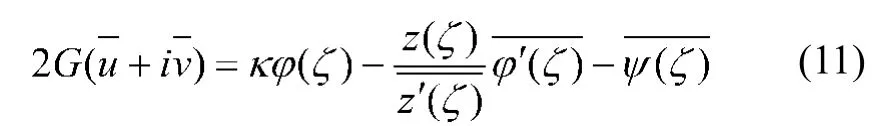
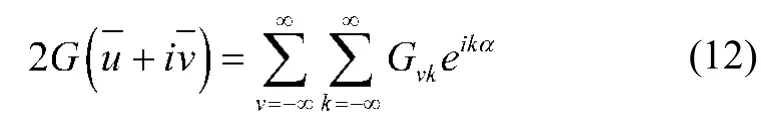
对于地表边界ζ =σ有

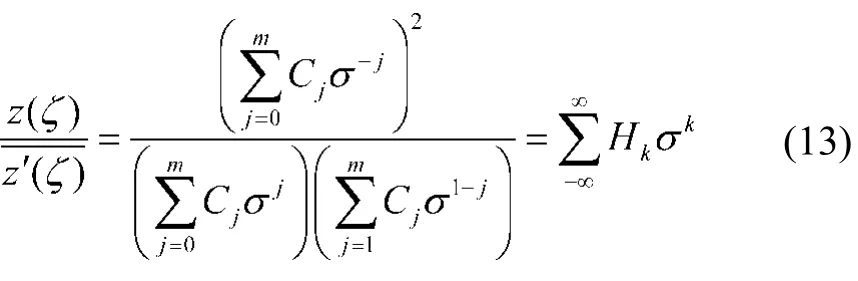
在实际计算时取Hk的项数为s。Hk的值可根据式(13)左右两侧σ同幂次系数相等来求得。

将式(12)、(13)代入式(11)并化简后可得

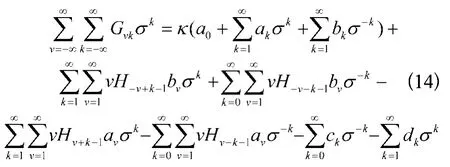
比较上式等号左右两边关于的同幂次系数得

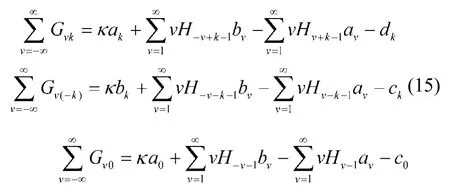
联立式(10)、(15)即可求得ak、bk、ck、dk的值。需要注意的是，根据Verruijt的研究，仅靠式(10)、(15)是无法求得唯一的ak、bk、ck、dk，在实际计算中也验证了这个结论。需根据ak、bk、ck、dk的收敛性来补充一个方程[2]，首先令a0=0计算当k足够大时ak的值(设此时ak=a)，再令a0=1计算当k足够大时ak的值(设此时ak=b)，则合适的a0取值为

之后再根据式(10)、(15)计算ak、bk、ck、dk的值，将这些求得的值代回式(6)、(7)即可得到所要求的复应力函数。

4 应力及位移的求解

根据求得的φ(z)、ψ(z)及式(1)、(2)即可求出某一点处的σij、ui，需要注意的是，在点∞处由式(2)计算得到的ux不一定为0，设此点处ux=，由于本文将参考点取在此处，为满足改点ux=0的条件，将每一点处所求的ux都减去，即：

由于增加一个刚体位移并不会改变应力，显然这样处理后依然满足应力边界条件。

5 算例及与其验证

设某一矩形顶管其隧洞几何尺寸及坐标如图1所示，图中a=2 m，b=2 m，h=10 m。根据地质报告，取泊松比v=0.3，弹性模量E=10 MPa。矩形顶管存在均匀与非均匀收敛模式，在实际工程中其位移模式一般为非均匀变形，故可设=设计要求地层损失率控制在5‰以内，可得

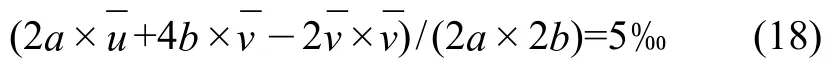
在将所有的边界条件都表示成的级数形式后，利用Matlab将4节求解过程编写为程序，其求解由计算机自动完成。在实际求解过程中，φ(ζ )、ψ(ζ )的项数、Ek的项数、Gk的项数、Hk的项数不可能取无限，一般可取一个较大的数，本文求解过程中分别取为100、50、50、50。同时为了验证本文求解的正确性，将所求结果与有限元结果相比较。有限元采用线弹性模型，采用与解析解相同的参数，并采用平面应变模型进行模拟。考虑到顶管的埋深约为10 m，且宽度较窄而长度较长，空间效应明显，故本模型宽度方向取距顶管边约5倍开挖深度即总宽度为10 m×5×2=100 m，在深度方向上取10 m×5=50 m。

5.1 位移分析

图3为顶管施工引起的地表沉降对比图。从图中可以看出：复变函数计算所得的沉降与有限元结果吻合较好，经计算两者的误差在1%左右；矩形顶管开挖引起的地层位移也近似呈正态分布，反弯点大致位于1.5倍的开挖深度处，地表沉降主要发生在4倍的开挖深度范围内；埋深越大沉降越大，地表沉降最小，其值约为洞室边界沉降的70%左右。

5.2 应力分析

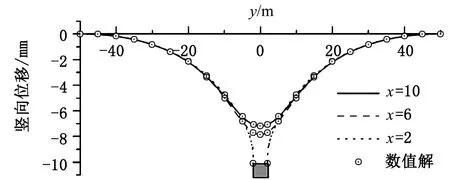
图3 地表位移分布Fig.3 Deformation of the surface

图4为不同位置处的σx、σv应力分布图，图中的负值表示压应力。从图中可以看出：除部分角点处，复变函数计算所得的应力结果与有限元结果吻合较好，经计算两者的误差在1%左右；在角点处有限元所得的应力集中系数比本文结果大得多，这是因为有限元在建模时采用了直角，引起了较大的应力集中；对σx而言，最大的压应力发生在顶板与侧帮的角点处，最大压应力值约为40 kPa，最大拉应力发生在侧帮与底板的角点处，最大拉应力约为35 kPa；对σv而言，最大的压应力发生在顶板与侧帮的角点处，最大压应力值约为30 kPa，最大拉应力发生在侧帮与顶板的角点处，最大拉应力约为25 kPa。

有限元结果可以认为是精确解，从本文解法与有限元解的对比来看，在大部分点处本文结果与有限元结果相差不大，因此总体来说本文的解法是精确的，可以满足工程精度要求。

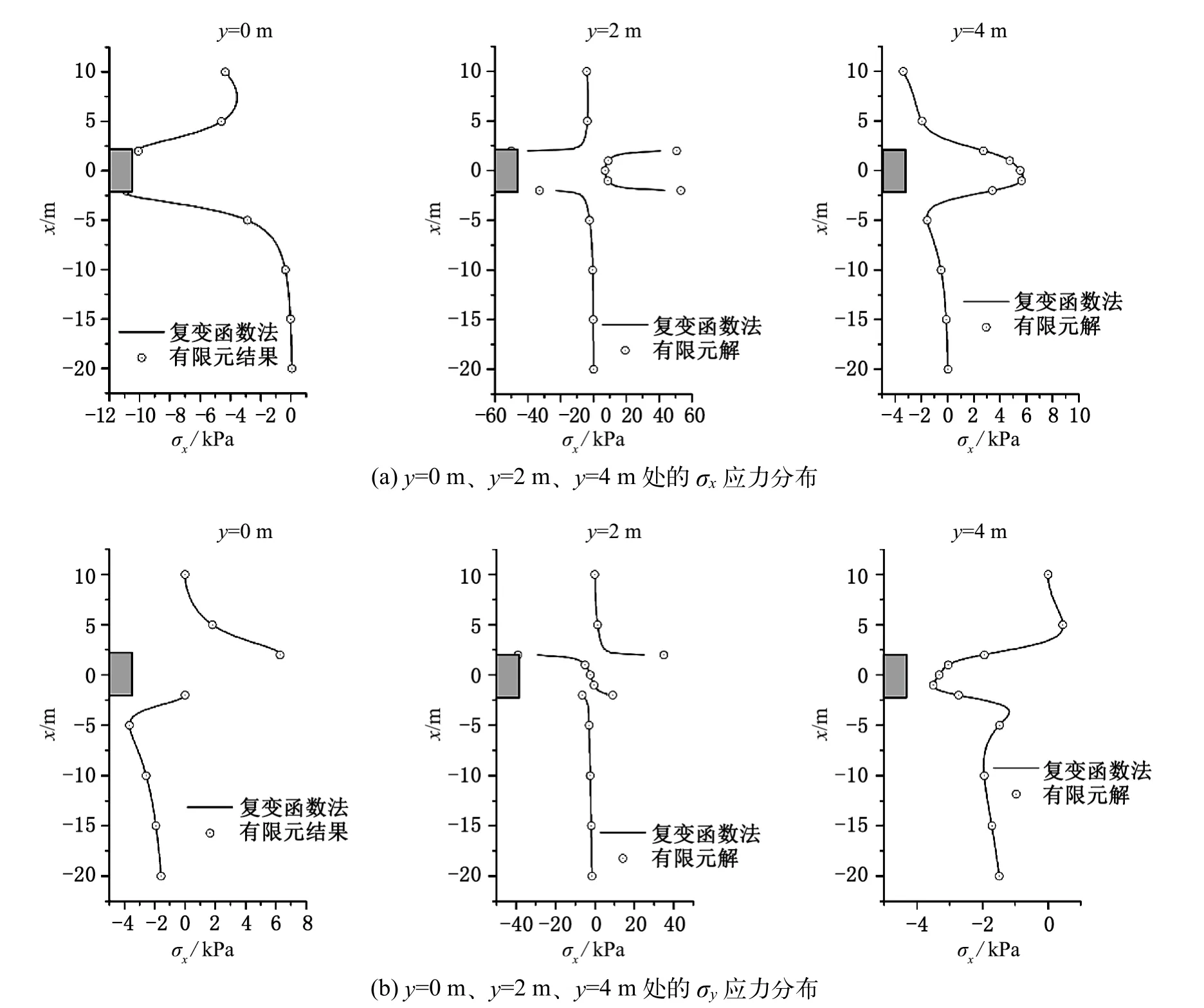
图4 不同位置处应力分布图Fig.4 Stresses curves at different position

6 结论

1)半无限体矩形隧洞开挖问题复变函数法的难点在于保角映射函数的求取。采用本文提出的先将含矩形隧洞的半无限域映射为中间域，再将中间域映射为同心圆环域的“两步走”的求解方法可较方便地求解出该函数，且便于应用现有研究成果。

2)从本文解法与有限元解的对比来看，在大部分点处本文结果与有限元结果相差不大，误差在2%左右。本文给出的求解方法求解过程步骤清晰、收敛快、精度高，易于编程实现，有很强的可操作性。

3)对于类似本文的工程，矩形顶管开挖引起的地层位移近似呈正态分布，反弯点大致位于1.5倍的开挖深度处，地表沉降主要发生在4倍的开挖深度范围内；顶管施工引起的地表变形约为洞室边界位移的70%左右。

4)对σx而言，最大的压应力发生在顶板与侧帮的角点处，最大压应力值约为40 kPa，最大拉应力发生在侧帮与底板的角点处，最大拉应力约为35 kPa；对σv而言，最大的压应力发生在顶板与侧帮的角点处，最大压应力值约为30 kPa，最大拉应力发生在侧帮与顶板的角点处，最大拉应力约为25 kPa。

[1] 陈子荫.围岩力学分析中的解析方法[M]. 北京：煤炭工业出版社，1994：46-73.

[2] VERRUIJT A. A complex variable solution for a deforming circular tunnel in an elastic half-plane[J].International Journal for Numerical & Analytical Methods in Geomechanics，1997，21(21)：77-89.

[3] STRACK O E，VERRUIJT A. A complex variable solution for a deforming buoyant tunnel in a heavy elastic halfplane[J]. International Journal for Numerical & Analytical Methods in Geomechanics，2002，26(12)：1235-1252.

[4] 童 磊，谢康和，卢萌盟，等.盾构任意衬砌变形边界条件下复变函数弹性解[J].浙江大学学报：工学版，2010 (9)：1825-1830.

[5] 江学良，杨 慧，曹 平.边坡下伏地下圆形洞室的弹性应力解析[J].计算力学学报，2012，29(1)：62-68.

[6] LU Aizhong，ZENG Xiantai，XU Zhen. Solution for a circular cavity in an elastic half plane under gravity and arbitrary lateral stress[J].International Journal of Rock Mechanics & Mining Sciences，2016，89：34-42.

[7] 陈行威，宋振森.加劲十字形轴压杆考虑初始扭转缺陷的扭转位移函数[J].河北工程大学学报：自然科学版，2016，33(3)：8-12.

[8] SCHINZINGER R，LAURA PAA. Conformal mapping：methods and applications[M]. New York City：Dover Publications，2003.

A complex variable solution for rectangle pipejacking in elastic half-plane

LI Xinyuan，LIU Guobin
(School of Civil Engineering，Tongji University，Shanghai 200032，China)

Considering the boundary and the surface conditions，the stress fi eld and displacement fi eld caused by the construction of the shallow rectangular pipe jacking are solved by the complex function method. According to the Riemann’s existence theorem and basic complex variable theory，a conformal mapping function which can transform the half-plane with a rectangle cavity into the concentric ring is established. The both sides of boundary conditions equation are expanded into Laurent series，and then the coef fi cients of complex stress function are solved by power series method. The derived solution is applied to an example and a comparison is made using FEM method to show the accuracy of the methods，the results of this paper are almost the same as those of the FEM method，and the error is about 2%. The result shows：(1) The method presented in this paper is applicable to a shallow buried rectangular tunnel；(2) The complex function method proposed in this paper is characterized by clear steps，fast convergence and simple operation.

half-plane；rectangle pipejacking；complex variable solution；power series method.

TU4

A

1673-9469（2017）04-0001-04

10.3969/j.issn.1673-9469.2017.04.001

2017-08-11

国家自然科学基金资助项目(51378389)；国家重点基础研究发展计划(“973”计划)项目(2015CB057806)

李新源(1986-)，男，山东潍坊人，博士，主要从事地下结构受力研究。