岩石非线性黏弹塑性蠕变模型研究

杨广雨，王 伟，熊德发，冯晓伟

(1.河海大学 岩土力学与堤坝工程教育重点实验室，江苏 南京 210098；2.河海大学 岩土工程科学研究所，江苏南京 210098)

岩石非线性黏弹塑性蠕变模型研究

杨广雨1，2，王 伟1，2，熊德发1，2，冯晓伟1，2

(1.河海大学 岩土力学与堤坝工程教育重点实验室，江苏 南京 210098；2.河海大学 岩土工程科学研究所，江苏南京 210098)

提出一种新的非定常粘滞系数的流变元件，然后将提出的非线性流变元件引进到Poyting-Thomson模型中，从而建立了新的非线性黏弹塑性流变模型，该模型不但可以较好地模拟岩石蠕变三个阶段，而且模型参数较少。推导出模型的本构方程及蠕变方程，并探讨了模型参数的辨识方法，最后利用本文建立的非线性流变模型所得到的理论曲线与砂岩蠕变试验曲线进行对比分析。结果表明：本文建立的非线性流变模型具有较高的准确性及合理性。

岩石流变；非线性元件；加速蠕变；饱依丁-汤姆逊模型

岩石流变是影响岩土工程长期稳定性的一个重要因素，在对岩石流变现象的模拟方法中，利用弹簧、滑块及黏性元件模拟岩石蠕变现象是较为常用的方法，但是传统的基本元件都为线性元件，只能模拟岩石蠕变的前两个阶段，即衰减阶段和稳定阶段，无法模拟加速蠕变阶段。因此，很多学者开始将非线性流变元件引入到现有的流变模型中去以便能模拟岩石加速蠕变阶段[1-11]。本文针对传统的Poyting-Thomson模型无法模拟岩石加速蠕变阶段的不足，通过引进非定常黏滞系数的黏滞元件，建立了非线性流变模型，拟合结果表明本文建立的模型的正确性及可行性。

1 岩石非线性黏弹塑性流变模型

1.1 改进的非线性流变元件及模型本构关系

本文在熊良宵等[12]构建的非线性流变元件的基础上通过改进提出一种新的非定常黏塑性元件，该元件中的黏滞系数是与流变时间t有关的函数，改进后的非线性流变元件示意图见图1。

图1 本文使用的非线性流变元件Fig.1 The non-linear rheological component

改进后的元件满足以下应力-应变关系。

将上述改进后的流变元件（下图2的第1部分）与传统的饱依丁-汤姆逊体模型（下图2的第2部分）进行串联，从而可以得到新的非线性流变模型，见图2。

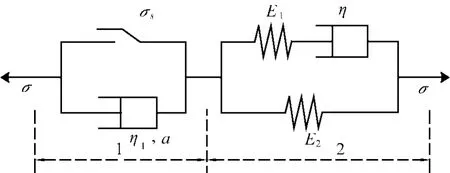
图2 本文建立的岩石非线性流变模型Fig.2 The nonlinear rheological model of rock

由于本文建立的模型的本构关系受到应力σs的影响，所以，需要根据应力σ与σs关系来建立模型的本构关系，由模型的性质可知，需要分两种情况来建立模型的本构关系，第一种是当σ ≤ σs时，第二种情况是当σ ＞σs时。下面对这两种情况分别推导其本构关系。

当σ ≤ σs时，此时由于滑块受力小于摩擦阻力，滑块无法滑动，因此图2的第一部分应变为零，第一部分相当于一个刚体，对模型的本构关系没有影响，此时模型就变成传统的饱依丁-汤姆逊模型。

当σ ≤ σs时，模型的状态方程为

式中：σEi(i=1，2)为对应弹性元件所受的应力，εEi(i=1，2)为对应元件的应变，εηi(i=1，2)为模型中对应黏性元件的应变，σηi(i=1，2)为模型中对应黏性元件所受到的应力，ηi(i=1，2)为对应黏性元件的黏滞系数，ε时模型的应变，ε·为模型的应变率。

利用上述得到的(2)、(3)式，可以求得模型的本构关系。

当σ ≤ σs时，模型本构关系为

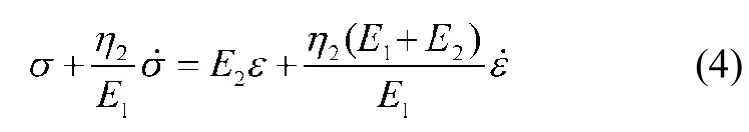
当σ ＞ σs时，模型的本构方程为

1.2 非线性流变模型蠕变特性分析

为了探究建立的模型具有哪些流变特性，首先需要建立σ =σ0时的岩石流变方程，根据两式，利用Laplace变换求解方程时，首先需要求解当时间t=0时的初始条件。当t=0时，应力状态不同时，初始条件也是有差别的。下面分别给出当时间t=0时σ ≤ σs与σ ＞ σs的初始条件。

当σ0≤ σs时，σ0为定常数，ε(0)为

当σ0＞ σs时，σ =0，σ¨=0，

根据上述初始条件结合式，利用Laplace变换和逆变换可以求得模型的蠕变方程。

当σ0≤ σs时，模型的蠕变方程为

当σ0＞ σs时，模型的蠕变方程为

当σ0≤ σs时，上式模型的蠕变方程(6)对t求一阶导数及二阶导数，由此可得

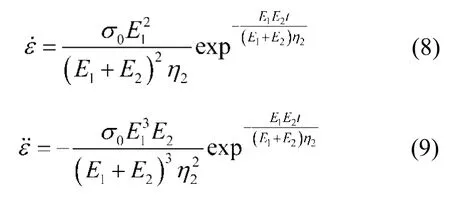
当σ0＞ σs时，上式模型的蠕变方程(7)对t求一阶导数及二阶导数，由此可得

2 流变模型的试验验证

2.1 模型参数辨识方法

本文建立的非线性流变模型共有5个参数即E1、E2、η2、η1、a，这也是本文模型的一大优点。文中建立的流变模型可以按照有无加速蠕变阶段的条件分为稳态蠕变（岩石蠕变只有前两个阶段）和不稳态蠕变（岩石应力超过σs，蠕变有三个阶段），当模型为稳态蠕变时，采用最小二乘法进行参数拟合，参数拟合的效果往往较好。当岩石蠕变类型为不稳态蠕变时，直接用最小二乘法来参数拟合的效果往往不满足要求。所以本文使用流变曲线分解法进行参数辨识，根据岩石试验曲线的特点，辨识出加速蠕变的临界时间tc，在tc之前，模型用最小二乘法求得模型中的E1、E2、η2、η1，然后用得到模型做出在tc之后的理论蠕变曲线，将岩石蠕变试验曲线与得到的理论曲线做差得到差函数φ(t)，然后，将差函数φ(t)与时间t作幂指函数拟合，从而求得模型参数a，至此，模型中的全部参数均已求出。

2.2 模型验证

本文是通过引用王伟等[12]砂岩流变试验数据来验证模型是否正确合理，该砂岩的分级加载流变试验曲线见下图3。

图3 砂岩分级加载流变试验曲线Fig.3 The rheological test curve in the conditon of sandstone graded load

根据图3可知，当对砂岩施加第一级荷载时，砂岩产生了瞬时的弹性变形，在荷载小于150 MPa之前，在每一级荷载条件下，砂岩的应变率逐渐趋于一个大于零的定常值。当荷载大于150 MPa时，砂岩的应变率趋于无穷大，此时砂岩发生加速蠕变破坏。

在本文建立的非线性流变模型的基础上，引进王伟等[13]砂岩流变试验数据，当施加的荷载小于150 MPa时，利用最小二乘法进行模型参数辨识，当荷载大于等于150 MPa时，利用上节介绍的流变曲线分解法进行参数辨识。经过曲线拟合可得该模型在每级荷载条件下的参数，结果见表1。

表1 流变模型参数拟合结果Tab.1 The parameter fi tting results for Rheological model

根据表1得到的模型参数，带入到理论公式里，然后将理论流变曲线与砂岩流变试验曲线进行对比分析，对比结果见下图4。

图4 砂岩流变试验曲线与模型理论曲线对比图Fig.4 Comparison chart of rheological test curve and model theory curve of sandstone

根据图4 的对比曲线可知本文建立的非线性流变模型不仅可以很好地反映岩石蠕变前两个阶段，也能够较好地模拟岩石加速蠕变阶段，从而证明了本文建立的非线性流变模型的正确性。

3 结论

1）使用改进的非线性流变元件，建立了新的饱依丁-汤姆逊模型，推导了其本构方程及蠕变方程，分析了流变模型的非线性流变特性，当σ0≤ σs时，本文建立的模型可以反映岩石蠕变的前两个阶段，当σ0＞σs时，非线性流变模型可以较好的模拟岩石蠕变全过程。

2）将模型得到的理论蠕变曲线与砂岩流变试验曲线进行对比分析，两者的曲线比较吻合，这表明了本文建立的非线性流变模型的正确性。

[1] 邓荣贵，周德培，张倬元，等.一种新的岩石流变模型[J].岩石力学与工程学报，2001(6)：780-784.

[2] 康永刚，张秀娥.一种改进的岩石蠕变本构模型[J].岩土力学，2014(4)：1049-1055.

[3] 张树光，王有涛，林晓楠.东梁煤矿非饱和砂岩黏弹塑性蠕变分析[J]. 辽宁工程技术大学学报：自然科学版，2017(2)：127-131.

[4] 曹树刚，鲜学福.煤岩的广义弹粘塑性模型分析[J].煤炭学报，2001(4)：364-369.

[5] 黄海峰，巨能攀，周 新，等.基于改进Burgers模型的片岩蠕变特性研究[J].水电能源科学，2017(3)：119-122.

[6] 胡 波，王宗林，梁 冰，等.岩石蠕变特性试验研究[J].实验力学，2015(4)：438-446.

[7] 刘东燕，赵宝云，朱可善，等.砂岩直接拉伸蠕变特性及Burgers模型的改进与应用[J].岩土工程学报，2011(11)：1740-1744.

[8] 蒋昱州，徐卫亚，王瑞红.角闪斜长片麻岩流变力学特性研究[J].岩土力学，2011(Z1)：339-345.

[9] 韦立德，杨春和，徐卫亚.基于细观力学的盐岩蠕变损伤本构模型研究[J].岩石力学与工程学报，2005(23)：4253-4258.

[10] 蔡 煜，曹 平.基于Burgers模型考虑损伤的非定常岩石蠕变模型[J].岩土力学，2016，(Z2)：369-374.

[11] 张华宾，闵小东，张顷顷.基于Matlab的岩石蠕变模型参数辨识算法设计[J].河北工程大学学报：自然科学版，2016，33(3)：29-32.

[12] 熊良宵，杨林德，张 尧.岩石的非定常Burgers模型[J]. 中南大学学报：自然科学版，2010(2)：679-684.

[13] 王 伟，吕 军，王海成，等.砂岩流变损伤模型研究及其工程应用[J].岩石力学与工程学报，2012(Z2)：3650-3658.

Study on nonlinear viscoelasto-plastic creep model of rock

YANG Guangyu1，2，WANG Wei1，2，XIONG Defa1，2，FENG Xiaowei1，2
(1.Key Laboratory of Ministry of Education For Geotechnical & embankment Engineering，Hohai University，Nanjing 210098，China；2.Geotechnical Research Institute，Hohai University，Nanjing 210098，China)

In this paper，a new rheological component with unsteady viscous coef fi cient is proposed，then connecting the proposed nonlinear rheological component with the Poyting-Thomson model，a new nonlinear viscoelastic-plastic rheological model is established. The model can not only simulate the three stages of rock creep，but also has less model parameters. In this paper，the constitutive equation and creep equation of the model are deduced，and the identi fi cation method of the model parameters is discussed. Finally，the theoretical curves obtained by the nonlinear rheological model established in this paper and the sandstone creep test curves is compared and analyzed. The results show that the nonlinear rheological model established in this paper has good accuracy and rationality.

rock rheology；nonlinear component；accelerative creep；Poyting-Thomson model

TU43

A

1673-9469（2017）04-0023-04

10.3969/j.issn.1673-9469.2017.04.006

2017-07-14

国家自然科学基金资助项目(11672343，51679069)；中央高校基本科研业务费专项资金资助项目(2016B20214)

杨广雨(1993-)男，河南驻马店人，硕士，从事岩石力学与工程方面的研究。