基于多目标结构参数优化的微创手术机器人设计

王 丽，王瑞强，赵保亮，陈 蓟，王 南

(1.河北工程大学 机械与装备工程学院，河北 邯郸 056038；2.中国科学院 深圳先进技术研究院 集成所认知技术中心，广东 深圳 518055；3. 暨南大学 第二临床医学院深圳市人民医院，广东 深圳 518055)

基于多目标结构参数优化的微创手术机器人设计

王 丽1，2，王瑞强1，2，赵保亮2，陈 蓟3，王 南1

(1.河北工程大学 机械与装备工程学院，河北 邯郸 056038；2.中国科学院 深圳先进技术研究院 集成所认知技术中心，广东 深圳 518055；3. 暨南大学 第二临床医学院深圳市人民医院，广东 深圳 518055)

为提高手术机器人的通用性，根据不同微创手术工作空间要求和操作要求设计了一种具有8自由度的通用性微创手术机器人，构造了包含运动学和动力学特性的多目标优化函数，利用遗传算法对含有运动学和动力学的双响应指标进行优化获得了具有较高灵活度的结构参数，为后续结构设计提供了良好的理论基础。

微创手术机器人；多目标优化；固有频率分析；遗传算法

随着生物工程、自动化技术及机器人技术的发展，机器人辅助微创手术已广泛应用于实际临床手术中。迄今为止，用于临床最典型的商业外科手术机器人系统是美国Intuitive Surgical公司于2003年开发出的Da Vinci微创外科手术系统[1]，该系统结构紧凑，且操作臂被安装在移动平台上便于在手术室内移动，但由于其高昂的价格和维护费用在推广使用上受到了很大的阻力。国内在手术机器人研究领域也取得了一些成果，如中国科学院深圳先进技术研究院认知技术中心胡颖研究员团队研制的脊柱微创手术机器人[2]；2013年哈尔滨工业大学、南开大学与中国人民解放军总医院在国家863计划下联合研制的腹腔镜外科手术机器人系统[3]。本文基于多目标结构参数优化设计了一种微创手术机器人，通过构型综合分析设计了一款具有8自由度通用型持镜机器人，提出基于运动学和动力学的多目标优化方法，对机械臂固有频率响应函数和运动学响应函数进行了综合优化，并验证了动力学和运动学优化结果。

1 构型综合分析

微创手术是一种通过位于患者腹部的5个直径大约为5～20 mm的切口进行操作的手术类型，医生通过内窥镜反馈到显示器上的病灶视图进行手术操作，根据临床经验，置入内窥镜的切口直径大小为5 mm且位于肚脐下方，其他四个切口均为手术操作切口，包括医生操作口和助手操作口，其中主操作手(右手)切口大小有12 mm，另外一个操作切口大小为5 mm。目前最常见的持镜手术是腹腔镜手术和鼻内镜手术，在腹腔镜手术中，其工作空间是一个以切口为顶点，锥角为60°半径为100 mm的圆锥体[4]，如图1(a)，鼻内镜手术也具有同样形状的工作空间，其工作空间为锥角40°，半径100 mm的锥体[5]，如图1(b)。通用持镜机器人应该满足不同微创手术工作空间要求，通过分析腹腔镜手术和鼻内镜手术工作空间，综合得到两种手术工作空间的共同点。

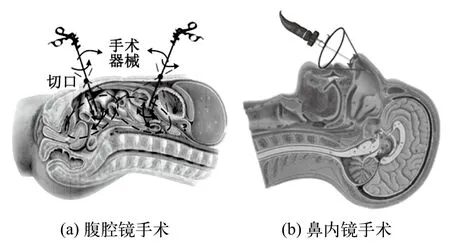
图1 微创手术工作空间Fig.1 Workspace of minimally invasive surgery

为保证在手术过程中避免手术器械的运动对手术切口造成损伤，需要设计一种在手术过程中提供空间不动点的机构使得手术器械始终绕手术切口这个固定点做三个转动和一个移动，包括绕y轴的俯仰运动、绕x轴的偏航运动、绕手术切口轴线的旋转运动以及沿着手术切口轴线的进给运动。在机器人设计过程中必须保证夹持手术器械的手臂满足四个自由度，本文采用了一种远心定位结构(Remote Center of Motion，简称RCM)，利用机械结构约束方法确保实现手术器械绕x轴偏航运动（关节5）和绕y轴的俯仰运动（关节6），如图2所示。远心定位结构末端安装直线运动关节（关节7）和旋转关节（关节8）实现手术器械沿着手术切口轴线的进给运动以及绕手术切口轴线的旋转运动。通过设计合理的自由度和杆件参数使得微创手术机器人满足不同的微创手术要求。

图2 RCM结构简图Fig.2 The CAD model of RCM

此外为了将手术器械置于手术区域，还需要至少三个自由度的位置调整机构，本文所设计的位置调整机构由三个旋转关节构成，其中包括一个水平面内的旋转关节(关节2)和两个垂直平面内的旋转关节(关节3、4)，3R关节在多臂协同操作中极大的减少了相互碰撞；另外，位置调整关节还增加了一个调整整体机器人到一个适应手术床高度的移动关节（关节1）。微创手术机器人整体置于可移动小车上，增加了机器人的移动性，如图3所示。

图3 微创手术机器人结构简图Fig.3 The CAD model of the universal robotic holder

2 运动学指标

通过分析微创手术工作空间要求及所需自由度，机器人结构包括姿态调整结构和位置调整结构。位置调整机构具有一个调整整体机器人到一个适应手术床高度的移动关节和三个旋转关节，姿态调整机构由一个RCM机构、一个直线运动关节和一个旋转关节组成，实现内窥镜在两个方向上以手术切口为不动点的旋转以及沿内窥镜自身轴线的进给和旋转，因此，本文设计的微创手术机器人有8自由度。考虑到第一个高度调整关节只用于机器人术前粗调整阶段，以及第八旋转关节并不影响末端器械的位置和姿态，因此本文只对剩余的6个关节进行运动学分析。基于D-H参数法建立了微创手术机器人特定姿态下的运动学分析模型，如图4，机器人各关节变量的D-H参数表见表1。

图4 微创手术机器人运动学分析模型Fig.4 The kinematics model of the robot

表1 机器人D-H参数列表Tab.1 The D-H parameters of the robot

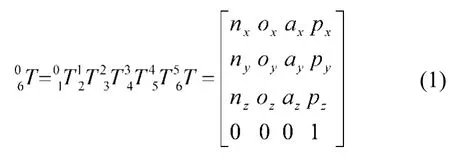
式中，nx=s5(c1c4s23-s1s4)-c1c4s23；ny=s5(c1c4-s1s4s23)+s1s5c23；nz=c5s23-c4c5s23；oy=s1s4s23-c1c4；oz=-s1c23；ax=-c5(s5c23+c4c5s12+s4s23)-s1s4c5-s1s4；ay=c1(c4+s4s5)+s1(c4c5s23-s4s23-s5c23)；az=-s1c23-s5s23-c4c5s23；pz=l1+l2s2+l3s23-l4(s5s23-c4c5c23)；px=l2c1c2+l3c1c23-l4(s1s4c5-c1c4c5c23)+c1s5c23py=l4(c1s4c5-s1c4c5c23-s1s5c23)+l3s1c23-l2s1c2。式中，ci=cosθi；sj=sinθj；sij=cos(θi+θj)；sij=sin(θi+θj)。

对于微创手术机器人，末端点的运动范围在满足实际手术需求的情况下，应该具有更好的灵活性和协调性，机械臂的位置调整部分是用于调整末端内窥镜到达患者病灶位置处，这部分的结构参数以及运动性能影响着术前调整的灵活性，因此有必要对其进行结构参数的优化。考虑3R旋转关节（第2、3、4关节），对杆长l2和l3进行优化，计算得到以第二个旋转关节坐标系为参考系的雅克比矩阵：

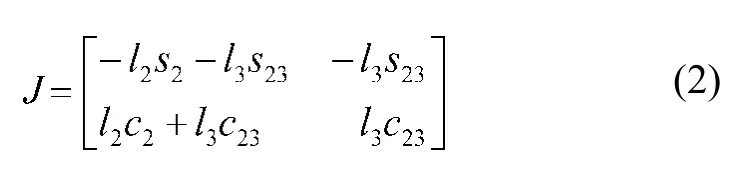
由于机构的灵活性指标与其姿态有关，很难十分准确地衡量一个机构的性能，Salibury和Craig利用雅可比矩阵J(q)的条件数作为衡量机器人灵巧度指标[6]，条件数越小，机构的灵活性越好。雅克比矩阵J条件数的定义为：

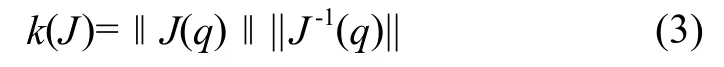
式中，当J为非奇异矩阵且JTJ为正定阵时，因此J的谱范数是该矩阵的最大奇异值，J-1的谱范数是J的最大奇异值的倒数。

3 动力学指标

为了获得动力学目标函数，基于Ansys Workbench软件建立机构的有限元模型，根据实验设计改变结构尺寸参数(杆长l2和l3)进行多次模态分析，提取机构的一阶固有频率。由于机构本身比较复杂且零部件比较多，需要对模型进行预处理将其简化，删除与机构主体功能无关的安装孔、轴承、螺钉等，由此建立有限元分析模型。

本文采用CCD实验设计方法进行二因子三水平实验设计建立二次响应面的模型，实验中分别用+1、0、-1表示每个变量的上限值、中间值、下限值，如表2所示。各个变量水平值与变量优化范围的对应值，根据实验设计结果分别进行模态分析提取一阶固有频率响应值如表3所示。

表2 变量与相对应的实际值Tab.2 Coded factors and their corresponding actual values

CCD实验设计的响应变化采用多元回归技术可以表示为二阶多项式：

表3 实验设计及其响应值Tab.3 The designed matrix of CCD and the corresponding experimental response data

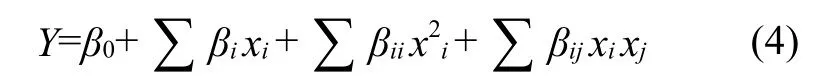
其中Y代表预测响应；xi和xj代表输入变量的实际值，如表3所示；β0是截距项，是常数；βi是各因素线性效应的量化；βii是各因素二次效应的量化；βij是两种因素之间交互作用的量化；采用最小二乘法拟合的响应曲面函数为

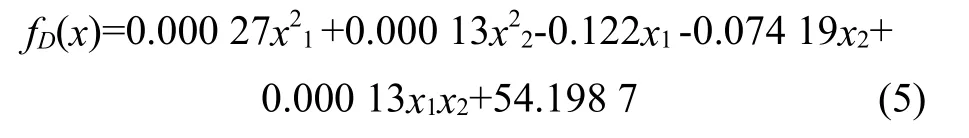
4 基于遗传算法的多目标优化

遗传算法是以Darwin的进化论和Mendel遗传学说为基础求解问题的方法，遗传算法在每个迭代步骤中修改个体解决方案的种群，随机地从当前种群中选择个体作为父辈，计算下一代“父体”，然后利用这些“母体”产生下一代，连续若干代后，种群朝着优化解的方向进化。基于运动学参数指标条件数和动力学的参数指标建立优化目标函数为F(x)。

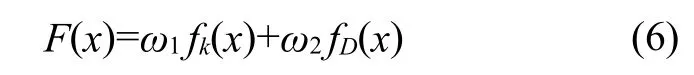
式中fk(x)为运行学参数指标，fk(x)=k(J)，fD(x)为动力学参数指标，ω1、ω2为加权因子，分别为0.5。

文章使用Matlab自带的遗传算法与直接搜索工具箱来执行优化过程，经过100次迭代得到优化变量为l2=289.99 mm，l3=232.99 mm时，目标函数值F(x)最小，如图5(a)所示为目标函数值分布图，图5(b)验证了当l2=289.99 mm和l3=232.99 mm时机构条件数k最小，将优化目标杆长圆整成l2=290 mm，l3= 232 mm，此时机构整体具有较好的灵活性。

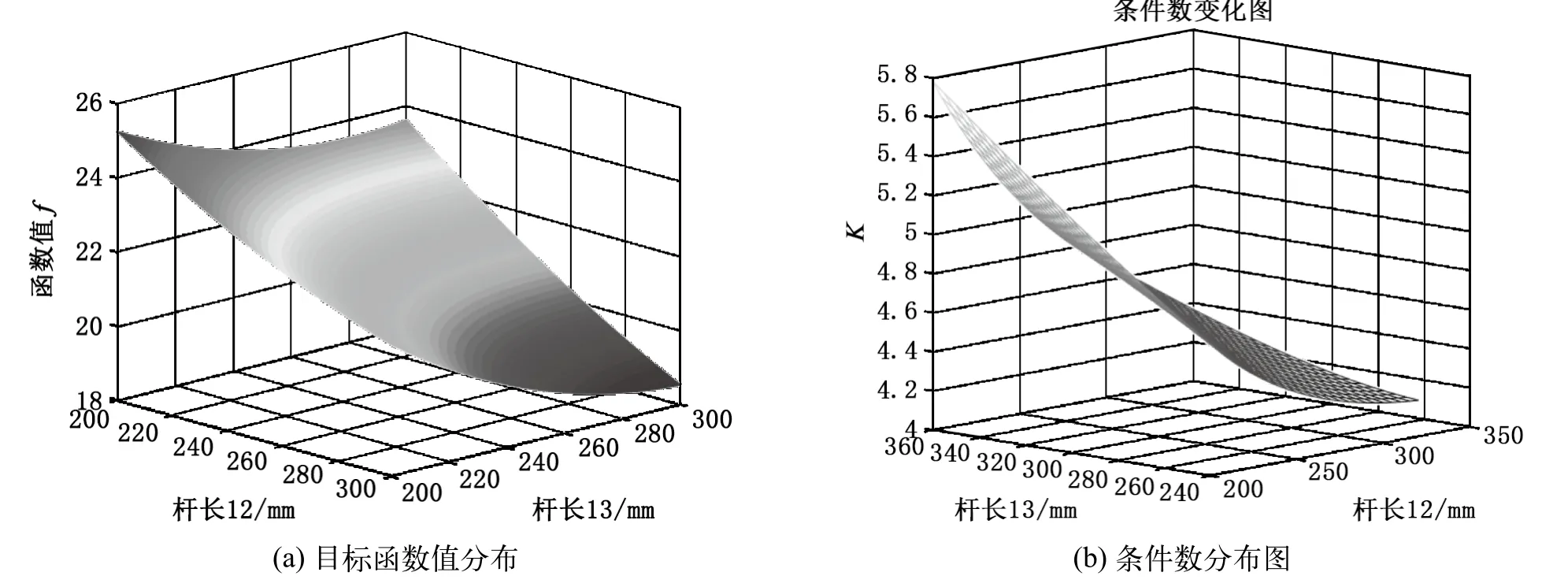
图5 目标函数值及条件数分布图Fig.5 The distribution curve of objective function value and condition number

将一阶固有频率作为动力学优化对象，当目标函数值最小时，此时，杆长l2和l3分别为290、232 mm，一阶固有频率为21.315 Hz，图6所示为当杆长l2=290 mm，l3= 232 mm时的六阶模态分析图。在一阶频率响应变形中，主要的变形量是沿着X轴方向摆动；在二阶频率响应变形中，主要的变形量是沿着Y轴方向的振动；在三节频率响应变形中，主要的变形量是RCM的转动；在四阶频率响应变形中，主要的变形量是3R关节绕着轴向转动(绕着X轴的转动)；在五阶频率响应变形中，主要的变形量是RCM绕着个关节轴向转动(绕着Z轴的转动)；在六阶频率响应变形中，主要变形量是绕着X轴的转动。

图6 优化后六阶模态分析Fig.6 modal analysis after optimization

综上所述，当杆长l2=290 mm和l3=232 mm时为包含运动学和动力学良好特性的结构尺寸参数。根据机器人运动学正解我们可以得到机器人工作空间如图7所示，它显示机器人末端可能达到的区域范围为半径大约为800 mm的半球，机器人的工作空间满足手术要求，此外，最后四个关节的运动范围不小于上文提到的要求，这也保证了夹持手术工具的局部运动，满足在手术中的要求。

图7 机器人工作空间Fig.7 Workspace of Robot

5 结论

本文通过微创手术要求和构型分析设计了一种具有8自由度通用性微创手术机器人，该机器人由位置调整部分和姿态调整部分组成，文章构造了包含运动学和动力学特性的多目标优化函数，利用遗传算法对含有运动学和动力学的双响应指标进行优化获得了具有较高灵活度的结构参数，并通过模态分析方式验证了在最优结构尺寸下的结构的稳定性，最后根据机器人运动学分析工作空间满足手术要求，这种兼顾运动学和动力学指标的优化设计方法为机器人缩短了开发周期并提供了较为全面的设计依据。

[1] GUTHART G S，SALISBURY J K J. The IntuitiveTM telesurgery system：overview and application[C]//IEEE International Conference on Robotics and Automation，Proceedings. ICRA. IEEE Xplore，618-621.

[2] JIN H，HU Y，TIAN W，et al. Safety analysis and control of a robotic spinal surgical system[J].Mechatronics，2014，24(1)：55-65.

[3] 马如奇.微创腹腔外科手术机器人执行系统研制及其控制算法研究[D].哈尔滨：哈尔滨工业大学，2013.

[4] LUM M J，ROSEN J，SINANAN M N，et al.Optimization of a spherical mechanism for a minimally invasive surgical robot：theoretical and experimental approaches[J]. IEEE transactions on bio-medical engineering，2006，53(7)：1440.

[5] TREVILLOT V，SOBRAL R，DOMBRE E，et al.Innovative endoscopic sino-nasal and anterior skull base robotics[J]. International Journal of Computer Assisted Radiology & Surgery，2013，8(6)：977-987.

[6] ANGELES J，ROJAS A.Manipulator inverse kinematics via condition number minimization and continuation[J].International Journal of Robotics & Automation，1987，2(2)：61-69.

Design of minimally invasive surgical robot based on multi-objective structural parameter optimization

WANG Li1，2，WANG Ruiqiang1，2，ZHAO Baoliang2，Chen Li3，WANG Nan1
(1. College of Mechanical and Equipment Engineering，Hebei University of Engineering，Hebei 056038；2.Shenzhen Institutes of Advanced Technology，Chinese Academy of Sciences，Guangdond，Shenzhen，518055；3. Shenzhen People’s Hospital，the Second Clinical Medical College of Jinan University，Guangdong Shenzhen，518055，China)

In order to improve the universality of the surgical robot，this paper analyzes the workspace and operation requirements of different minimally invasive surgery，and a universal surgical robot with 8 degrees of freedom has been designed. A multiobjective optimizing function with kinematic index and dynamic index has been constructed. The genetic algorithm is used for the optimization process and the structure parameter with high dexterity is obtained.

Minimally Invasive Surgical Robot；Multiobjective Optimization；Genetic Algorithm.

TP242

A

1673-9469（2017）04-0103-06

10.3969/j.issn.1673-9469.2017.04.023

2017-09-18 特约专稿

863重点项目（2015AA043201)；深圳市科技计划基础研究布局项目(JCYJ20150529143500954)

王丽(1990-)，女，甘肃天水人，硕士研究生，从事医疗机器人的研究。