混凝土断裂能的统计模型和标准值研究

丁力栋，丁晓唐，袁 存

(河海大学 土木与交通学院，江苏 南京 210098)

混凝土断裂能的统计模型和标准值研究

丁力栋，丁晓唐，袁 存

(河海大学 土木与交通学院，江苏 南京 210098)

采用三点弯曲法测定不同工况的混凝土断裂能，并就其中一个工况进行大样本试验。根据试验和收集文献中的数据建立断裂能基于混凝土强度和粗骨料最大粒径的双因素统计模型，将该统计模型与其他统计模型对比发现，其预测能力更好。应用统计分析软件SAS针对选用工况的试验数据进行了4种概率分布、5种拟合优度检验，得到该工况断裂能最符合的概率分布为对数正态分布，从而计算得到具有95%保证率的断裂能标准值GFk=66.0 N/m。

混凝土；断裂能；统计模型；概率分布；标准值

混凝土断裂能作为裂缝稳定性的判据，是非线性断裂力学在有限元分析计算中应用的重要参数，虽然国际材料和实验室联合会[1]已经推荐了实验室内测定混凝土断裂能的方法，但在工程现场预留出测定断裂能的试件还是有一定难度，因此国内外学者提出了一些用于预测混凝土断裂能的统计模型。徐道远[2]等和高泉[3]等研究了龄期对混凝土断裂能的影响，推导出了断裂能与龄期有关的统计模型。Wittman[4]研究了混凝土断裂能随混凝土强度的变化，拟合出了断裂能与混凝土强度之间的关系式。目前仅1990 CEB-FIP模式规范[5]列出了关于混凝土强度和骨料最大粒径的断裂能估算值表，但国外规范的混凝土强度等级是按照圆柱体抗压强度划分的，不便于国内使用。本文针对不同混凝土强度等级，不同粗骨料最大粒径的断裂能进行了研究，同时考虑到混凝土的离散性大，收集了文献中国内外较新的断裂能研究试验数据，将本文试验数据与文献中的数据作为一个数据库，建立了混凝土断裂能基于混凝土强度和粗骨料最大粒径的双因素统计模型，并分析了其预测能力。

目前应用有限元软件对结构进行分析计算越来越关注结构的损伤发展，在有限元软件ABAQUS的混凝土塑性损伤模型CDP中，需要应用混凝土断裂能这一参数。然而根据样本数量较小的试验数据得到的断裂能平均值并不能在设计施工中保证实际结构的安全性，本文提出了断裂能标准值的概念以提高结构的可靠度。在计算断裂能标准值之前，需进行大样本试验确定断裂能的概率分布，不同的概率分布对应不同的概率密度曲线，某一保证率下的断裂能也各不相同。本文对混凝土断裂能的概率分布和断裂能标准值进行了研究。

1 混凝土断裂能试验

1.1 试验设计

本文采用国际材料和实验室联合会推荐的带缺口的三点弯曲梁试件测定混凝土断裂能，试件长515 mm，宽100 mm，高100 mm，初始缝宽为3 mm，缝高比为0.3，跨高比为4。试验采用反向加载以消除试件自重的影响，因此需对国际材料和实验室联合会给出的断裂能计算公式进行修正，修正后的公式为

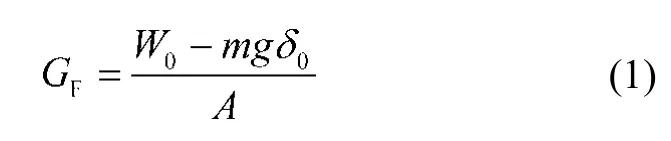
式中，GF为计算得到的混凝土断裂能；W0为外力做的功，等于荷载-挠度曲线下的面积；m＝m1+2m2，m1为梁支座之间的重量，m2为与试验机不相连，但直到试件破坏都加在试件上的加载装置的质量；A为断裂韧带的面积；δ0为梁最终破坏时的变形值。

为了得到混凝土强度和粗骨料最大粒径对混凝土断裂能的影响规律，并提出混凝土断裂能基于混凝土强度和粗骨料最大粒径的双因素统计模型，试验分为C20、C30、C40、C50四种混凝土强度等级，9.5、16、25 mm三种粗骨料最大粒径，共计12种工况，每种工况浇注4根三点弯曲梁试件用于测定断裂能，同时浇注3个标准立方体试件用于测定立方体抗压强度。试验中水泥为中联P·O42.5普通硅酸盐水泥，粗骨料为碎石，细骨料为河砂，粗细程度属于中砂，每个工况的配合比见表1。此外，为了研究混凝土强度C30，粗骨料最大粒径dmax=9.5 mm的混凝土断裂能标准值，另外浇注了36个三点弯曲梁试件，配合比与表1中的C30-1工况相同。所有试件浇注成型后静置48 h拆模，拆模后放入标准养护室内养护，由于浇注试件时在试模内插入钢片预制裂缝的效果不佳，因此本文试验试件的预制裂缝选择在试验前采用切割机切割而成。

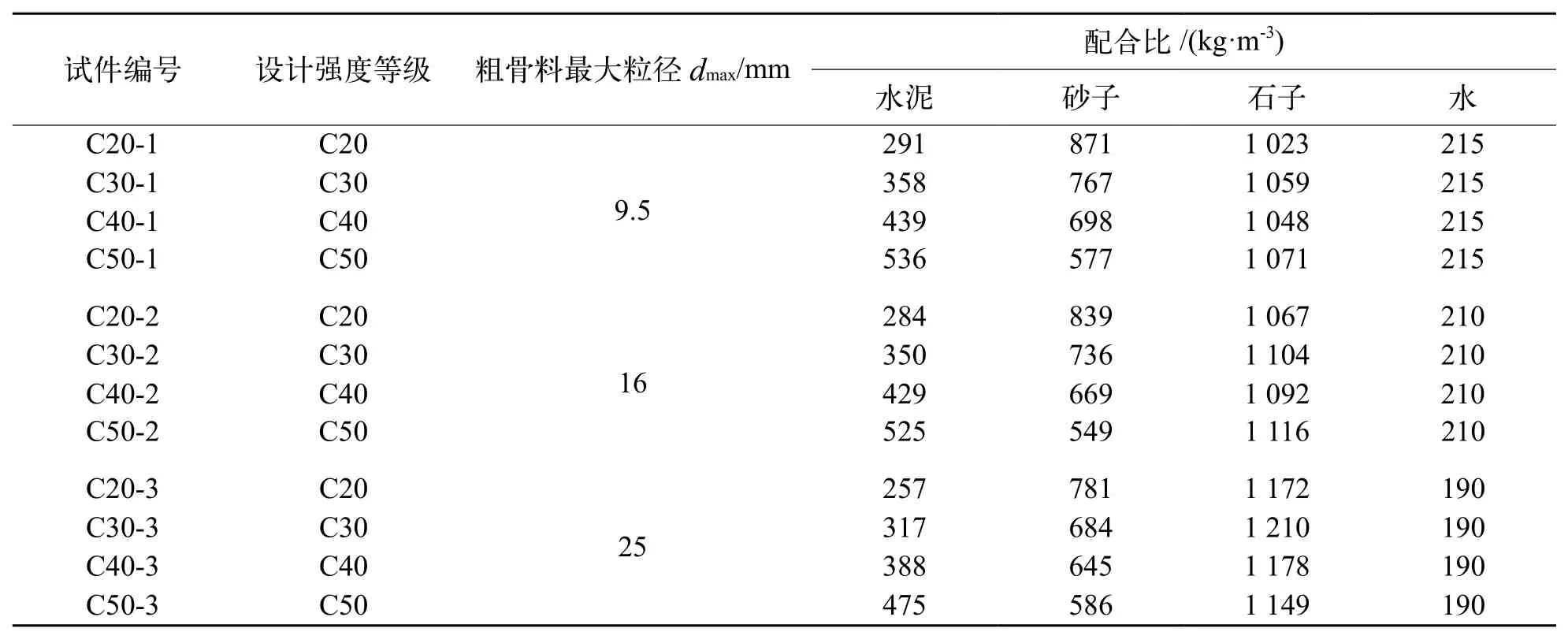
表1 混凝土配合比Tab.1 Mixture ratios of concrete

1.2 试验结果

表2列出了用于断裂能影响因素和统计模型研究的12个工况的立方体抗压强度平均值，荷载-挠度曲线中的最大荷载平均值与最大挠度平均值，以及根据荷载-挠度曲线计算得到的断裂能平均值。表3列出了用于断裂能标准值研究的实测的36个三点弯曲梁试件的最大荷载、最大挠度和断裂能，36个试件的断裂能平均值GF=105.35 N/m，考虑到能量参数的离散性大，因此在表3中右上角以*号标出了与断裂能平均值相差50%的试验数据，在计算断裂能平均值时未计入这部分数据。

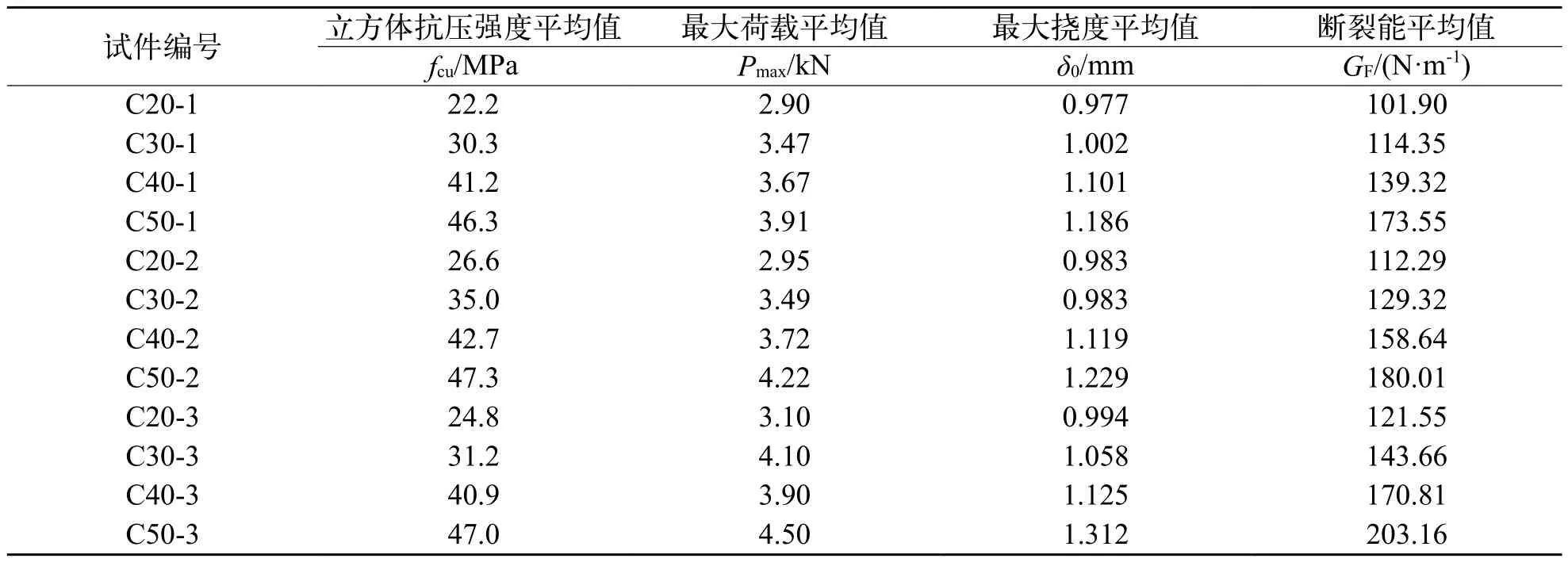
表2 用于断裂能影响因素和统计模型研究的试验数据Tab.2 Test data used to research factors affecting fracture energy and statistical model

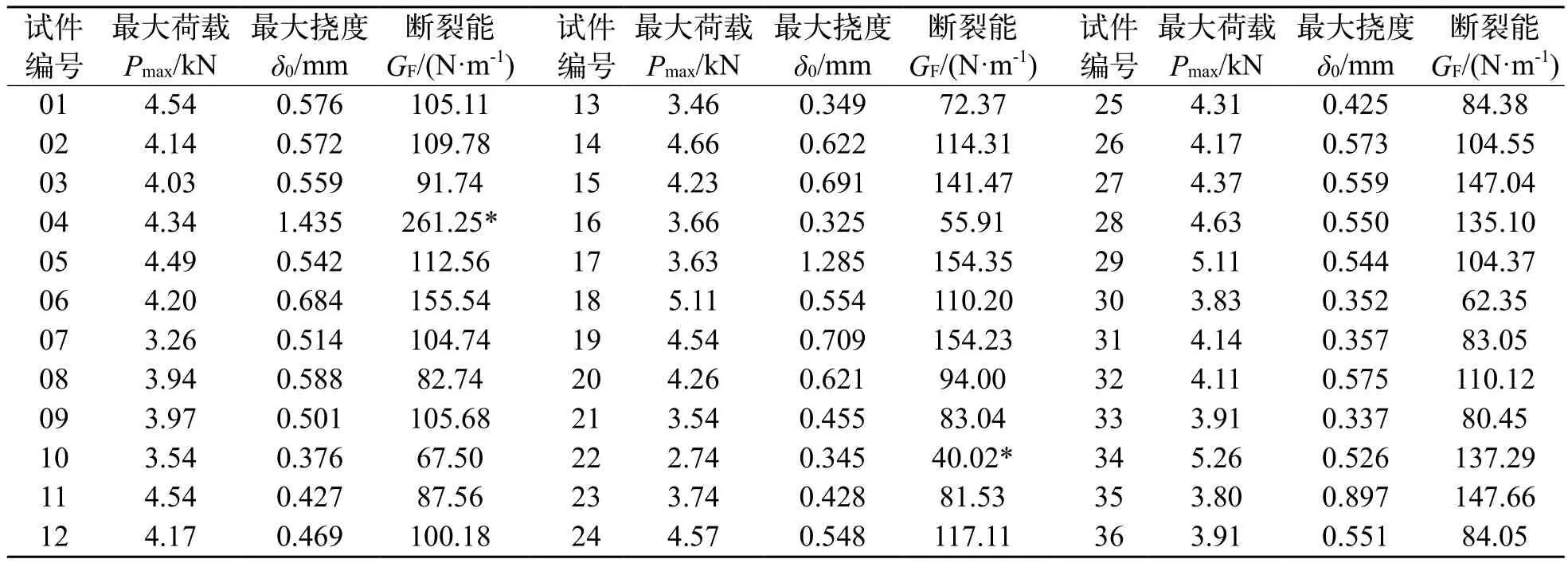
表3 用于断裂能标准值研究的试验数据Tab.3 Test data used to research characteristic values

2 断裂能影响因素及统计模型

2.1 强度和骨料粒径对断裂能的影响

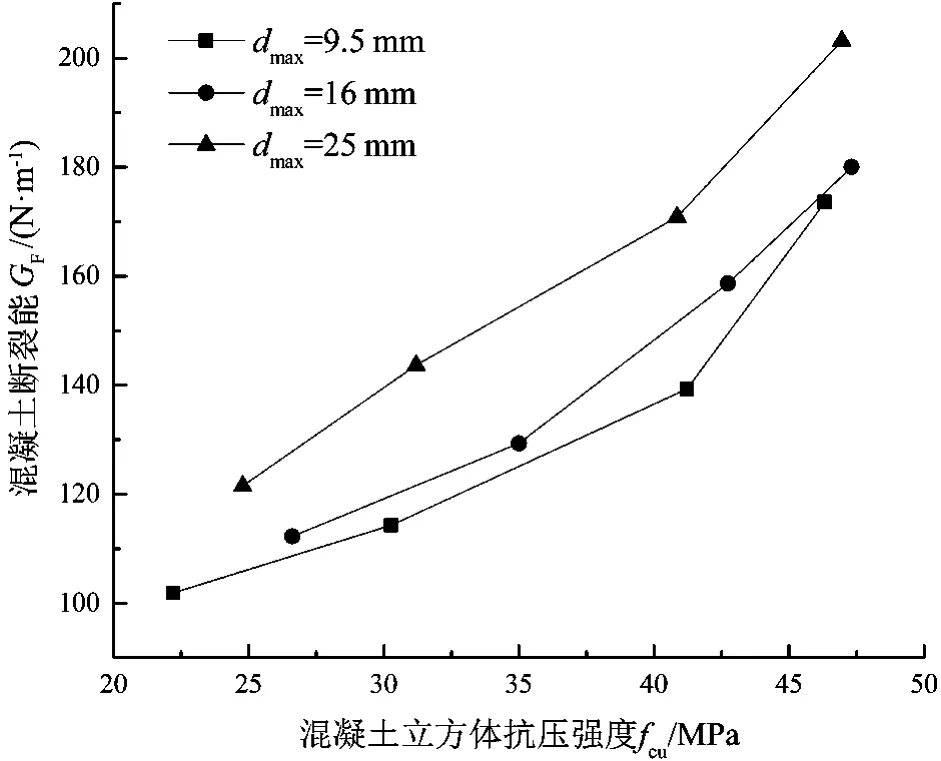
图1 混凝土强度对断裂能的影响Fig.1 Effect of concrete strength on fracture energy

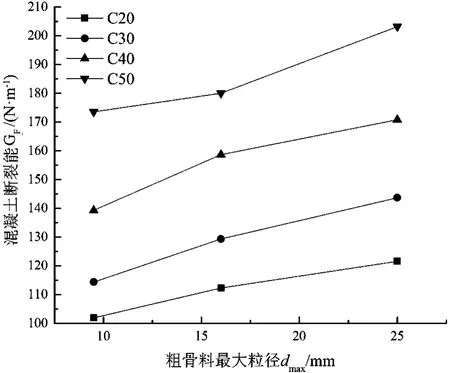
图2 粗骨料最大粒径对断裂能的影响Fig.2 Effect of maximum aggregate size on fracture energy

为了更直观地表现出混凝土强度和粗骨料最大粒径对混凝土断裂能的影响，将表2中的试验数据转化为图的形式。图1为混凝土断裂能随混凝土强度的变化曲线，从图中可以看出当混凝土强度不大于C50时，对于同一粗骨料最大粒径，混凝土断裂能随混凝土强度的增加呈增大趋势。这可解释为，混凝土强度增加，砂浆与粗骨料的粘结力也随之增加，因此混凝土断裂所需的能量越大。图2为混凝土断裂能随粗骨料最大粒径的变化曲线，从图中可以看出当粗骨料最大粒径不大于25 mm时，对于同一混凝土强度，混凝土断裂能随粗骨料最大粒径的增加也呈增大趋势。这是由于骨料对裂缝的扩展存在阻碍作用，随着骨料粒径的增大，迫使开裂路径发生变化，裂缝因此变得曲折，混凝土断裂能不断提高[6]。

2.2 断裂能统计模型

为了更准确地建立混凝土断裂能基于混凝土强度和粗骨料最大粒径的双因素统计模型，首先查阅了大量国内外较新的研究混凝土断裂能方面的文献，收集了65组可靠性较高的混凝土断裂能实测数据，称为统计数据库1，具体数值及取值依据参见文献[7]。在统计数据库1中加入表2的试验数据，称为统计数据库2。利用最小二乘法，分别根据统计数据库1和统计数据库2拟合得到的统计模型为式（2）与式（3），1990 CEB-FIP模式规范给出的统计模型为式（4）。

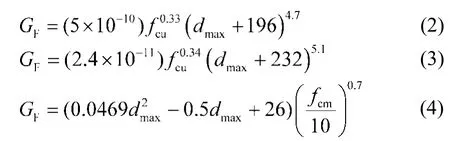
式中，fcm为圆柱体抗压强度平均值。

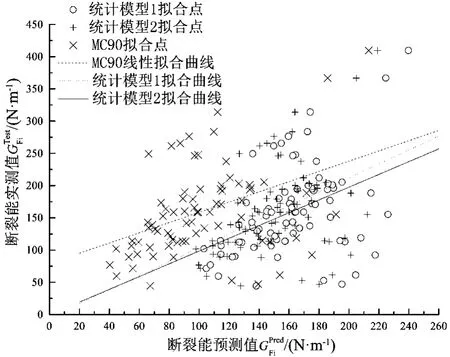
图3 断裂能预测值与实测值线性拟合图Fig.3 Linear fi t of predictive values and test values

为了衡量3个混凝土断裂能统计模型预测能力的好坏，将统计数据库2中混凝土抗压强度和粗骨料最大粒径原始数据分别代入式（2）、（3）、（4），得到基于统计数据库1、统计数据库2和CEB-FIP模式规范3个统计模型的断裂能预测值，并对断裂能预测值=X和断裂能实测值=Y的数据点进行线性拟合，拟合结果如图3所示。理想情况下，即统计模型足够精确，断裂能预测值与实测值应满足此时拟合出的直线的斜率为1，截距为0。

由图3可得，基于统计数据库1、统计数据库2和CEB-FIP模式规范3个统计模型线性拟合出的直线的斜率分别为1.08、0.99、0.79，截距分别为4.83、0.58、79.23。根据式（2）拟合的直线的斜率接近于1，截距接近于0，可以看出基于统计数据库1建立的统计模型能较好地反映混凝土强度和粗骨料最大粒径对断裂能的影响。根据式（3）拟合的直线的斜率更接近于1，截距更接近于0，说明基于统计数据库2建立的统计模型能更好地反映混凝土强度和粗骨料最大粒径对断裂能的影响，另一方面也说明了在统计数据库1中新加入的本文试验数据提高了统计模型的精度。而相对于式（2）与式（3）的预测值，CEB-FIP模式规范给出的断裂能统计模型预测值整体偏小。

3 断裂能概率分布及标准值

3.1 断裂能概率分布分析

为了得到混凝土强度C30，粗骨料最大粒径dmax=9.5 mm的混凝土断裂能标准值，首先应用统计分析软件SAS对36个试件的断裂能进行了概率分布分析，为增加概率分布的可信度，本文选用了4种常见的概率分布以及针对每一种分布进行了5项拟合优度检验。其中S-W检验仅适用于正态分布，不适用于Weibull分布和Gamma分布，K-S检验不适用于Weibull分布，当样本数量不大于2 000时，两者以S-W检验为准，具体检验结果如图4以及表4所示。

图4为根据断裂能频率分布直方图拟合得到的4条概率分布曲线，表4中的数值为某一检验针对该分布的实际显著性水平P值，用于判定假设检验结果。一般情况下，理论的显著性水平α=0.05，如果P＜α=0.05则拒绝原假设。由图4和表4可知，5种检验均表明该工况断裂能既服从正态分布又服从对数正态分布，但对数正态分布的P值大于正态分布的P值，对数正态分布的符合程度就比正态分布高。C-M检验和χ2检验下不拒绝Weibull分布，除了S-W检验之外的4种检验都不拒绝Gamma分布，但对数正态分布的P值均高于或略低于两种分布的P值，对数正态分布的符合程度比Weibull分布和Gamma分布高。所以该工况断裂能最符合对数正态分布，应根据对数正态分布来计算断裂能标准值。

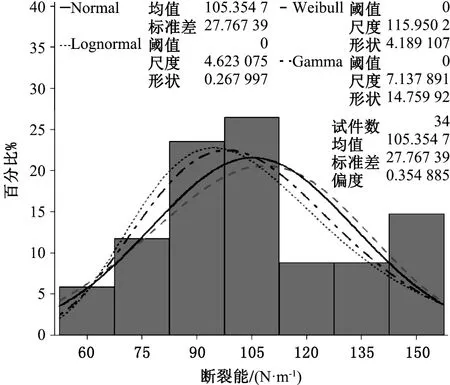
图4 断裂能概率分布Fig.4 Probability distribution of fracture energy

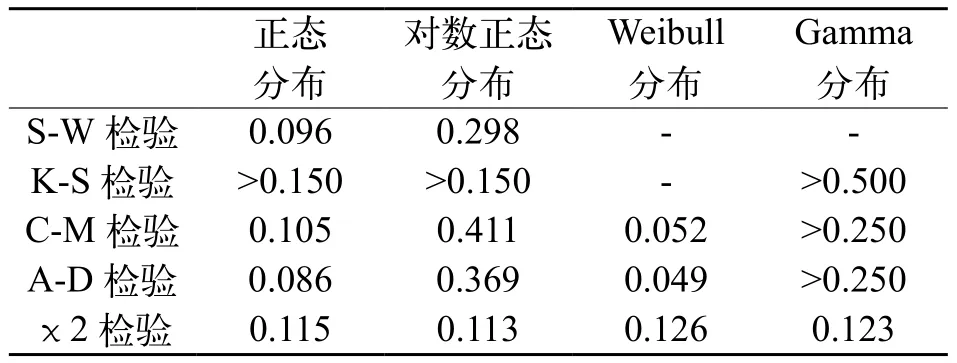
表4 断裂能拟合优度检验Tab.4 Goodness-of- fi t tests of fracture energy

3.2 断裂能标准值计算

设随机变量X表示某一个试件实测的混凝土断裂能，当X服从正态分布时，平均值μX=105.35 N/m，标准差σX=27.77 N/m，变异系数δX=σX/μX=0.264，即X～N(105.35，27.772)。当X服从对数正态分布时，InX服从正态分布，即InX～N(μInX，。由对数正态分布的性质可知：=In(1+)=0.067 4(N/m)2。取标准值的保证率为95%，则InX需大于u=μInX-1.645σInX=4.19 N/m，此时GFk=eu=66.0 N/m即为混凝土强度C30，粗骨料最大粒径dmax=9.5 mm的混凝土断裂能标准值。

4 结论

1）收集国内外文献中较新的65组混凝土断裂能实测数据，称为统计数据库1，基于统计数据库1建立的双因素统计模型能较好地反映混凝土强度和粗骨料最大粒径对断裂能的影响。在统计数据库1中加入本文试验数据，称为统计数据库2，基于统计数据库2建立的统计模型预测混凝土断裂能的精度更高，也从侧面体现了本文试验数据的合理性。1990 CEB-FIP模式规范给出的断裂能统计模型偏于保守，预测值整体偏小。

2）对混凝土强度等级C30，粗骨料最大粒径9.5 mm工况进行了大样本试验，用统计分析软件SAS确定该工况下的断裂能最符合对数正态分布，根据对数正态分布计算得到具有95%保证率的断裂能标准值GFk=66.0 N/m。

[1] RILEM Technical Committee 50-FMC. Determination of the fracture energy of mortar and concrete by means of three-point bend tests on notched beams[J]. Materials and Structures，1985，18(4)：287-290.

[2] 徐道远，陈里红，李国英，等.早龄期混凝土断裂参数KIc，GF的试验研究[J].河海大学学报，1991，19(3)：130-133.

[3] 高 泉，赵国藩，赵顺波. 龄期及粗骨料级配对高坝混凝土断裂能GF和断裂韧度KIc的影响规律[J]. 建筑科学，1994(3)：19-23.

[4] WITTMANN F H，ROELFSTRA P E，MIHASHI H，et al. In fl uence of age of loading，water-cement ratio and rate of loading on fracture energy of concrete[J]. Materials and Structures，1987，20(2)：103-110.

[5] CEB-FIP model code 1990，The CEB/FIP model code for concrete structures[S].

[6] 丁晓唐，袁 存，郑 艳.混凝土劈裂抗拉强度与轴心抗拉强度关系研究[J].河北工程大学学报：自然科学版，2016，33(1)：24-26.

[7] 袁 存.混凝土断裂能标准值及其在数值模拟中应用的研究[D].南京：河海大学，2016.

Research on statistical model and characteristic values for the fracture energy of concrete

DING Lidong，DING Xiaotang，YUAN Cun
(College of Civil and Transportation Engineering，Hohai University，Jiangsu Nanjing，210098，China)

The fracture energy of concrete for different cases is calculated by means of three-point bend tests，and large sample tests of one case are done. Based on the test data of this experiment and other articles，statistical model about fracture energy of two factors，concrete strength and maximum aggregate size，are established. Compared the statistical model with other models，the ability of prediction is better than other models，and it can prove rationality of test data indirectly. Statistical analysis system (SAS) is applied to compare four probability distribution and fi ve goodness-of- fi t tests，the most suitable probability distribution of test data is lognormal distribution. Based to lognormal distribution，the characteristic value of fracture energy is equal to 66.0 N/m，the reliability is not less than 95%.

concrete；fracture energy；statistical model；probability distribution；characteristic value

TU528.1

A

1673-9469（2017）04-0005-05

10.3969/j.issn.1673-9469.2017.04.002

2017-07-22

国家自然科学基金资助项目(51279052)

丁力栋(1993-)，男，浙江金华人，硕士，从事混凝土结构基本理论及近代计算方法方面的研究。