利用探究资源 激发学生潜能——讲评一道填空压轴题时所经历的三重境界

周德明 王华民 奚勇斌

(1，3 江苏省太湖高级中学 214125 2 江苏省无锡市滨湖区教研中心)

某市2016年秋学期高二数学期末检测填空压轴题14：已知直线ax+by+c=0始终平分圆C:x2+y2-2x+4y-4=0(C为圆心)的周长，过点P(6，9) 作直线l:(2a-b)x+(2b-c)y+(2c-a)=0的垂线，垂足为H，则线段CH长度的取值范围是．阅卷后的统计显示，本题得分率太低，一所四星级学校平均得分率不足3%，引起我们的高度重视，需要认真反思．

本题究竟难在何处？其一，信息量大，含两条直线、两个圆(其中一个隐含)，除两个变量x、y外还有三个参数a、b、c；其二，综合性强，不仅要利用对称、圆、最值等相关知识，还要利用轨迹、消元、配方法等多种思想方法；其三，需要挖掘两个隐含条件——直线过定点和垂足的轨迹是一个定圆．既要考查学生对信息的处理、对数学思想方法的掌握，又要考查学生的思维能力、运算能力，难度确实大．从被访谈的学生了解到，题中隐含的“直线过定点”信息，有少数学生能发现，但隐含的“定圆”信息，能发现的就寥寥无几了．

在试卷讲评时，笔者除了关注学生的回答和课堂气氛外，特别关注学生的思维活动，给他们足够的思考的时间、空间，结果意外发生了……．课后仔细品味，不由联想到佛家人生的三重境界“看山是山，看水是水；看山不是山，看水不是水；看山还是山，看水还是水.”

第一重境界——看山是山，看水是水

笔者所任教的班级为该校层次最好的班级，有42人，其中仅4人答案正确．既然试题过难，一般学生难以发现解题突破口．因此，试卷讲评时，采用难点分解、逐个突破的策略，设计了如下一些思考问题：

图1

问题1直线ax+by+c=0 始终平分圆C:x2+y2-2x+4y-4=0(C为圆心)的周长(图1)，说明什么？

学生众：直线过圆心，可得a-2b+c=0.

问题2直线l:(2a-b)x+(2b-c)y+(2c-a)=0有何特征？

学生1：c=2b-a代入直线l方程，化简可得a(2x+y-3) -b(x-4)=0.

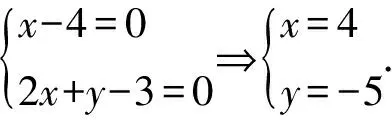
所以直线l:(2a-b)x+(2b-c)y+(2c-a)=0过定点M(4，-5).(利用消a或b代入，同样可以求得定点M(4，-5) ).

部分同学的表情显示：后悔，了解情况后得知，他们考试时没想到消元、转化，看到比较复杂的直线方程觉得无所适从，就放弃了.反映了学生对题中隐含条件挖掘不够，对于“式”的运算意识薄弱，能力亟待提高.

问题3过定点P(6，9)作l:(2a-b)x+(2b-c)y+(2c-a)=0的垂线，垂足H的轨迹是什么？

学生2：我列出了l与PH两条直线方程，构成方程组，求交点H的轨迹方程，感觉太繁了，算不下去.

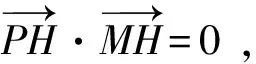
学生4(抢答)：如图2，因为PH⊥MH，所以点H在以PM为直径的圆上.

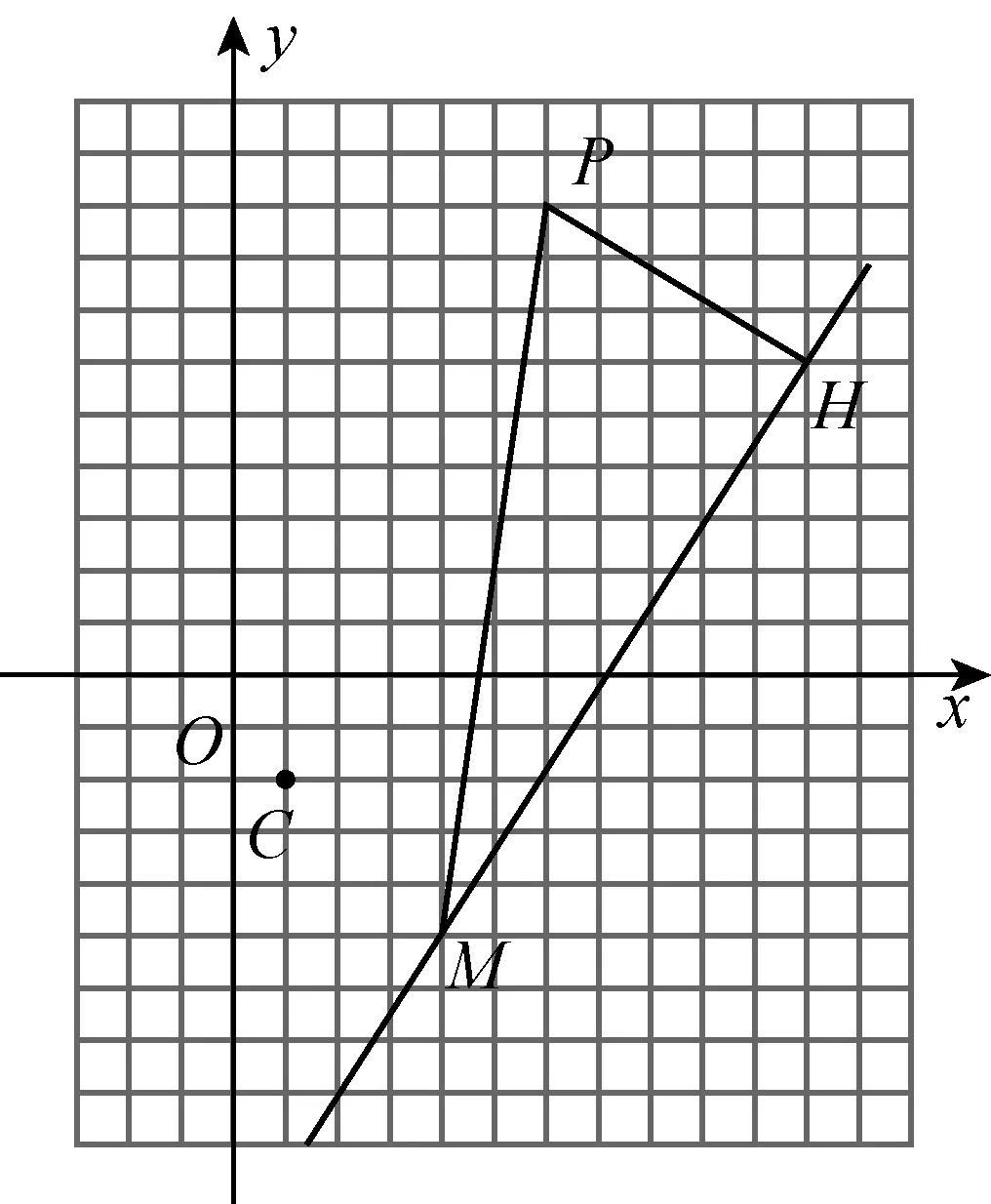
图2

学生3回答时课堂非常安静，还有很多同学在默默地点头.当学生4抢答时，课堂一下子活跃起来了.“哎，对啊！”他们开始懊悔自己没有画图，只是埋头苦算，还有些画了图，但没有将PM连起来，也就没有跳出“数”的囹圄，从“形”的角度重新认识它，真可谓“数”缺“形”时少直观！

问题4点C(1，-2)与垂足H的轨迹圆D：(x-5)2+(y-2)2=50位置关系如何？CH的最大、最小值分别是多少？CH长度的取值范围是．

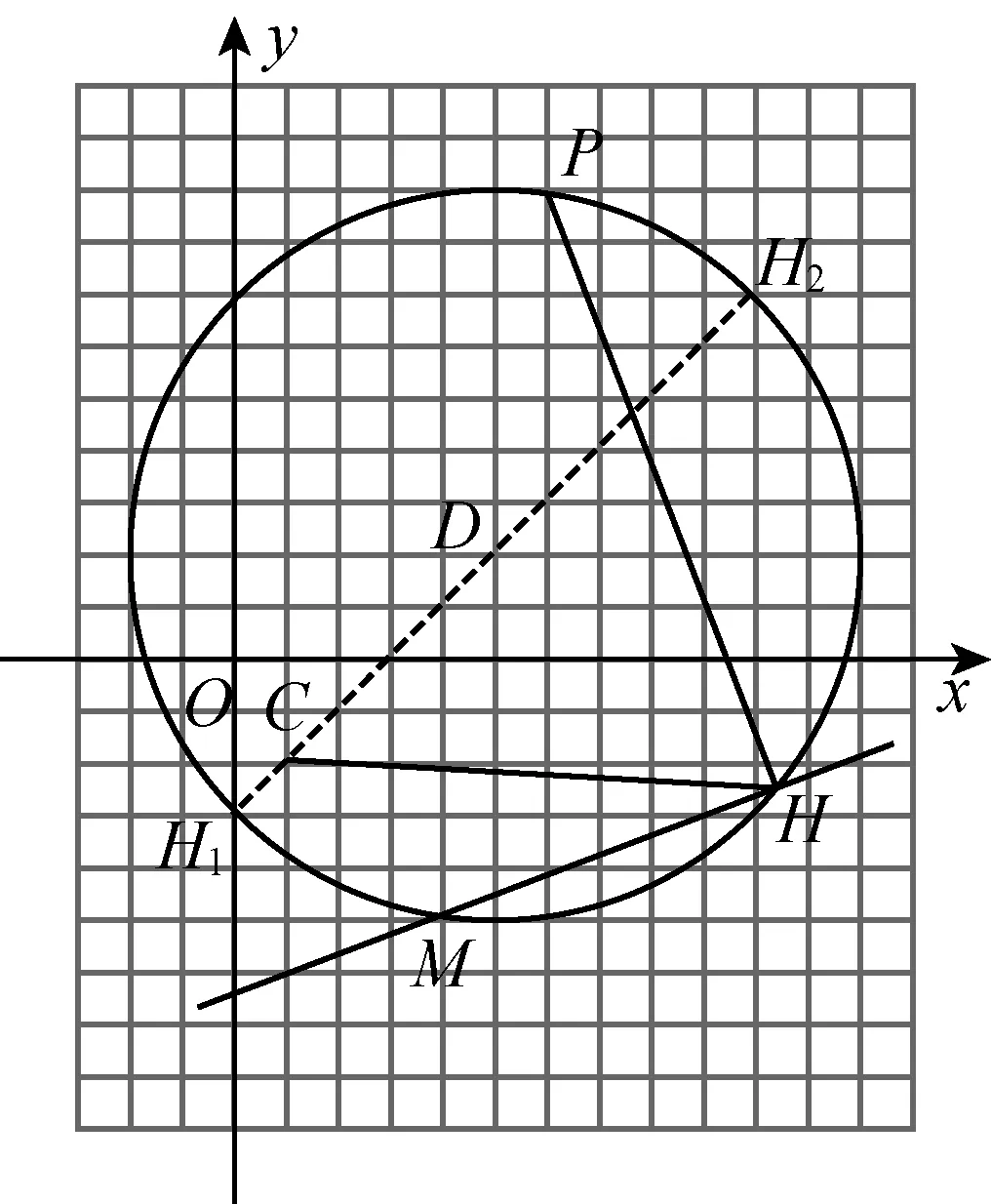
图3

学生众：点C在圆D内部时，

|CH|max=|CD|+R，|CH|min=R-|CD|，

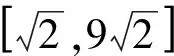
至此，本题解答应该是圆满的了，绝大多数同学都能看懂题目，厘清思路，基本达到了看山是山，看水是水的境界.

第二重境界——看山不是山，看水不是水

为了让学生保持积极思考状态，养成良好的思维习惯，帮助学生进一步学会思考、深化理解，笔者安排了解题回顾、反思的教学环节.

问题5解答本题的关键在哪？你是如何想的呢？

学生5：应该有两处，一是直线l所过定点问题，二是垂足H的轨迹问题.题中没有直接说明，相对比较隐含……

师：学生6做出了正确的答案，我们还是听听他的高见吧，说不定有惊喜呢！

图4

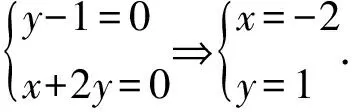
此时教室里鸦雀无声，观察学生的表情、神态大致有三种：一是张嘴望着学生6(佩服、质疑？)，二是托腮看着投影上学生6的解题过程(寻找着什么？)，三是低头在草稿纸上写着或画着什么(验证着什么？).时间飞逝，两分钟后有小声议论“答案巧了”、“肯定有问题”、“可能也行的” ……

学生7(托腮)：直线l不可能同时过两个定点M(4，-5)、N(-2，1).若过两个定点且不变成一条定直线，那么过点P(6，9)作l垂线的垂足H就应该是一个定点，CH的长度即为一个定值.

学生8(张嘴)：我说这个答案是巧了！

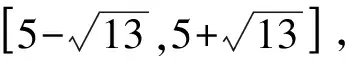
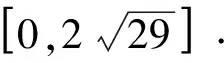
这个结果在我们意料之外，为验证它的正确性，笔者利用几何画板在图4的基础上改变P点的位置(如图5)，测得无论垂足H的轨迹是以PM为直径的圆，还是以PN为直径的圆，此结果CH长度的取值范围均相同.此时很多同学又认可了学生6的解答应该是正确的，但仍有部分同学不甘心.

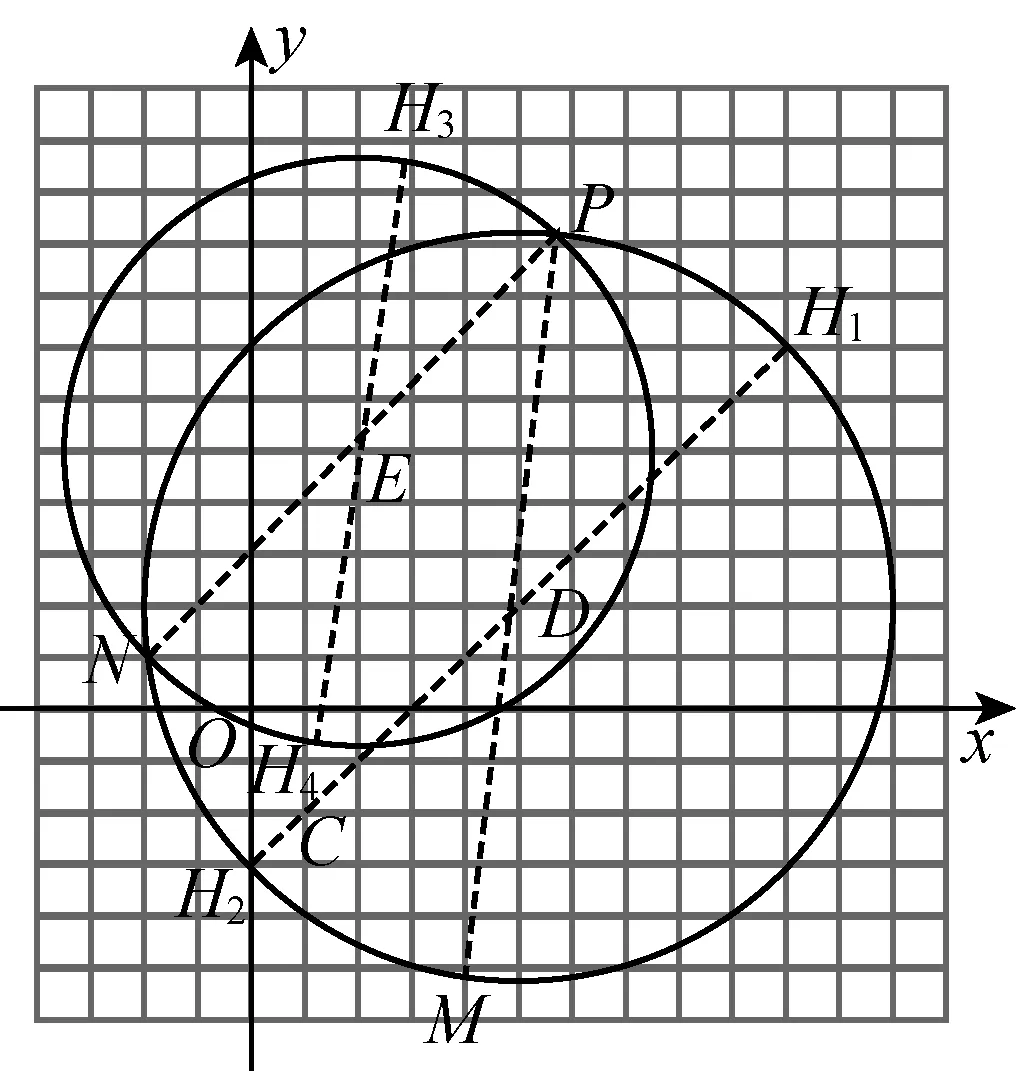
图5

至此，老师与同学经历了“对(答案)→错(猜想)→对(验证)→错(质疑)”的过程，到了看山不是山，看水不是水的境界.

第三重境界——看山还是山，看水还是水

为了弄清上述问题，笔者继续设计如下问题，请同学们再思考：

问题6直线l究竟是过定点M(4，-5)还是N(-2，1)？

学生11：应该是M(4，-5)，因为本题中a，b，c满足的条件是a-2b+c=0，而若过定点N(-2，1)，则-5a+4b+c=0，与条件不一致！事实上，直线bx+cy+a=0与直线l已不是同一条直线，它们经过的定点当然不同.如l1:y=k1x+3，l2:y=k2x-3，l:λ(k1x-y+3)+μ(k2x-y-3)=0，当λ=2，μ=1时，l过定点(0，1)，与l1，l2所过定点均不相同.显然不可用l2所过定点(0，-3)来代替l所过定点.

问题7答案巧在哪里呢？

叶澜教授说过“课堂应是向未知方向挺进的旅程，随时都有可能发现意外的通道和美丽的因素，而不是一切都必须遵守固定路线而没有激情的行程.”我再次把图5投影出来，让学生仔细观察.有同学发现，此时点C(1，-2)恰好是M(4，-5)与N(-2，1)的中点，是否玄机就在这里呢？

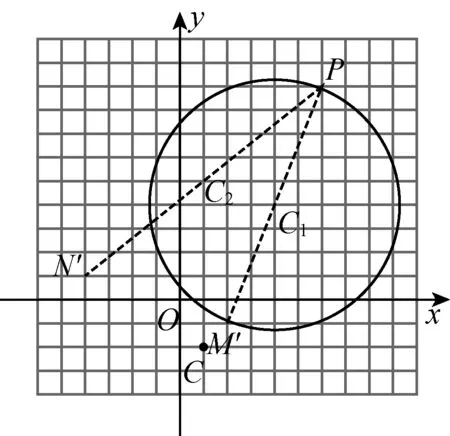
图6

显然范围是不一致的. 看来本题答案确实是巧了，那么为什么改变P点位置，结果仍一致呢？

思考若C是MN的中点，过M、N分别作动直线l1，l2，过平面内任一点P(与过M、N不重合)作直线l1，l2的垂线，垂足分别为H、Q，那么CH长度的取值范围与CQ长度的取值范围一定相同？

学生12：问题可抽象为H点的轨迹是以PM为直径的圆D，Q轨迹是以PN为直径的圆E(如图7)，|CH|max=|CD|+|DH|=|CD|+|PD|，|CQ|max=|CE|+|EQ|=|CE|+|PE|，又D、C、E分别为PM、MN、PN的中点，所以四边形CDPE为平行四边形，所以|CD|+|PD|=|CE|+|PE|，所以|CH|max=|CQ|max.同理，|CH|min=|CD|-|DH′|=|CD|-|PD|，|CQ|min=|EQ′|-|CE|=|EP|-|CE|，所以|CH|min=|CQ|min，则必有CH长度的取值范围与CQ长度的取值范围相同.

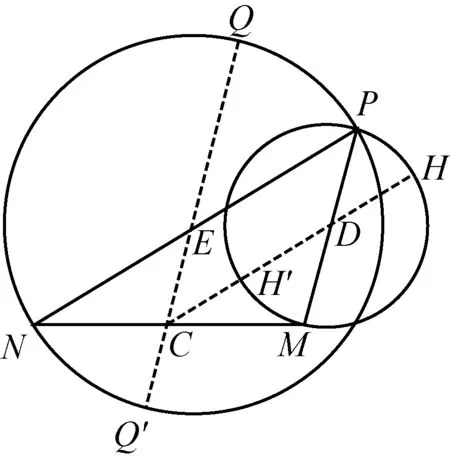
图7

太棒了！课堂上响起一片热烈的掌声.我不得不惊叹：学生真的是聪明的！他们每个人身上都蕴藏着无限的潜能.下课铃响了，同学们仍意犹未尽.

学生13：两定点一动点的问题，我想到的是椭圆.

学生14：两定点一动点的问题，我想到了双曲线.

学生15：两定点一动点的问题，我想到了阿波罗尼斯圆.

本节课又让我们见证了……

感叹：看山还是山，看水还是水.

之后，教师布置了一道巩固练习(2013年度江苏卷第17题改编)：在平面直角坐标系xOy中，点A(0,3)，圆C: (x-a)2+(y-2a+4)2=1，若圆C上存在点M，使MA=2MO，则圆心C的横坐标的取值范围是________.

一道检测的压轴题，由于得分率太低，几乎成了一道废题．大家都认同“错误可以转化为一种资源”的观点，而笔者对这道近乎废题进行再利用，把它作为课堂教学的一种探究资源，通过四个问题分解难点，发掘其隐含的思维价值．课上由于学生6的“独到解法”使问题变得扑朔迷离，教师又抓住这一种课堂的生成资源，还时间给学生进行数学探究，大大激发了同学们探究的热情、探究的欲望和创造的潜能，这不仅是知识的拓展、延伸，更是学生分析问题、解决问题的能力在提升，学生思维能力在发展，使得本题的思维价值得到充分的发掘．

俗语说：要给学生一滴水，老师就必须有一碗水，对于这类意外生成问题的处理，它考量的是教师的智慧和应变机制，对我们现代教师各方面能力(应变能力、扎实的基本功和几何画板等软件的应用)都提出了更高的要求，只有做到如王国维所说的“入乎其内”，才能“出乎其外”，愿我们师生且行且珍惜.