导问 让解题教学更有效

赵士元

(苏州市吴中区教学研究室 215107)

数学教学的目的是什么？《义务教育数学课程标准(2011版)》中明确提出：“体会数学知识之间、数学与其他学科之间、数学与生活之间的联系，运用数学的思维方式进行思考，增强发现和提出问题的能力、分析和解决问题的能力”.由此可知，数学教学的根本任务不只是培养学生解决现成问题的能力更是培养学生发现问题和提出问题的能力，世界著名科学家爱因斯坦说过：“提出一个问题往往比解决一个问题更重要．”，巴尔扎克也有过精辟的论述：“打开一切科学大门的钥匙毫无疑问是问号．”，我国古人也说过“学贵有疑”、“疑是思之始,学之端．”等．可以说发现问题是开启创新之门的一把金钥匙，一个人的创新能力某种程度上决定于他的问题意识和发现问题的能力．作为数学教学重要组成部分的解题教学理应担当起这种能力培养的任务，而“导问” 是培养学生问题意识和问题能力最有力的着力点，因为解题教学过程的本质就是一个提出问题、分析问题、解决问题的动态过程.因此，构建导问式解题教学便是值得每一个数学教育工作者去尝试的一个课题.所谓导问式解题教学是指根据不同的教学目标和教学内容呈现出来的以“问题和引导”为主的解题教学结构，它的主要特点是师生通过对问题本身的深入解读，启发学生思考探讨，引导学生提问，最终达到培养学生问题意识、提高学生提出问题的能力，并在此基础上生成学生智慧,达成教学目标，完成问题解决.导问式解题教学的两个关健词是“问”和“导”，其中“问”是灵魂，“导”是核心，导问式解题教学首先要解决的是“问什么？如何问？”，落实在实际的解题教学过程中是如何培养学生的问题能力，也就是导问式解题教学的关健点是导什么？如何导？

我们知道传统的解题教学是教师讲、学生听，其关注点是教师有没有讲透？学生有没有听懂？着重强调教师的主导作用，它的主要特点是教师单向灌输，学生被动接受.这种教学方式对提高学生解题的模仿能力有一定的帮助，但对增强学生问题意识和思维能力却是非常不利的.

导问式解题教学没有必须的操作程序但有其基本的操作规范，如何教会学生在处理具体问题时能通过提问的形式发现思路并在逐个解决所提问题的过程中提升分析问题和解决问题的能力呢？我想作为教师，首先要做好示范，因为很多学生都有一种模仿心理，他们会模仿教师的言行举止，更会模仿教师提出问题的方式，因此，教师应注意提问的言传身教. 在教学中，教师要结合学生生活和教学内容，有意识地为学生提问作示范，启发学生体会教师是如何提问题的，并把发现问题的思维过程展示给学生看，为学生能正确地、独立地质疑奠定基础.那么，如何引导学生提出问题呢？首先让我们看一个导问式解题教学的实际案例.

这是苏州、无锡、常州、镇江2017届高三第一次模拟考试的最后一题：

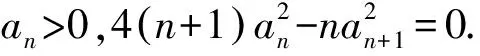
(2)若数列{bn}是等差数列，求实数t的值；

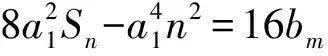
传统的教学方式往往是教师进行解答式讲评，这种讲评方式能使学生听懂解题过程，但对学生思维的培养和分析问题能力的提升并无益处，而导问式解题教学要求师生共同通过对问题的审视和思考，不断产生一系列小问题，从而完成将“综合问题”切割为“小问题”的任务，最终达到通过对若干小问题的突破完成综合问题的解决，导问式解题教学一般地需经历如下几个基本步骤.

首先是通过审题和分析，产生并提出问题．当拿到一个问题时首先要认真阅读，读懂问题的题设和目标，如果一遍没读懂须再读第二遍，二遍不行再读第三遍，深入阅读其义自明．

问题2：“数列{bn}是等差数列”是题目给出的条件，这一条件给出了什么信息？

问题3：第(2)小题目标是求t的值，需要我们做什么？要特别提醒自己的是“求t的值”，是一个求值问题！(求值两个字可多次重复)

问题5：第(3) 问中求满足条件的所有整数a1隐含着什么信息？(可多次重复“所有”、“整数”这几个关健词！)

第二步是通过教师引导，完善问题并寻找解决问题突破口.

对于问题2：数列{bn}是等差数列这一条件如何体现？这一问题与问题1类似，不过问题1涉及等比数列，问题2是等差数列；前者是判定，后者是性质，当学生熟悉了问题1后问题2便迎忍而解了.

明确了前述两个问题后，问题3的研究思路显得明晰一点了，条件是“数列{bn}是等差数列”，目标是求实数t的值.我们只要通过定义将“{bn}是等差数列”这一条件数学化，再用含有字母t的代数式表达这一数学化后的关系式进行求解.值得一提的是如下两点：

一是引导学生思考这一思路与解决什么样的问题有点类似？(解应用题)；二是由特殊到一般的关系，有时为减少运算量，可将“对任意正整数n，当n≥2时，都有2an=an-1+an+1”这一结论特殊化：2a2=a1+a3，从而由这一条件求出t的值(此时，求出的值可能有几个)，但由此求得的t只能满足2a2=a1+a3，能否满足更一般的“2an=an-1+an+1”，还需要进行验证.

最后一个问题是“求满足条件的所有整数a1”隐含着什么信息？此时教师应引导学生思考这一问题中的关健词：所有，整数！在教师这样的暗示下，大多数同学还是很难获得有用的信息的，此时教师要不断地轻声重复关健词，还可以自言自语轻声说“好象类似的问题有过，在什么时候呢？”、“为什么不是直接求a1而是要加个限定词呢？”等暗示性的语句，这时，教师务必放慢进度给学生充分的思考时间.如果在规定时间内仍然没有学生获得有用的信息，教师可提出另一个与之相关的问题，比如教师可以与学生一起分析：

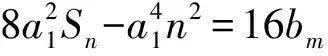
第三步是师生共同研究，优化并解决所提出的所有问题.

由于数列{bn}是等差数列，因此

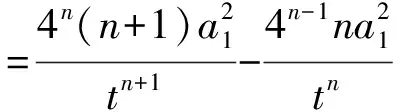
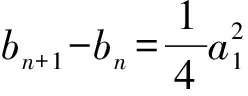
①对任意的正整数n,m，当n>m时都有bn=bm+(n-m)d，其中d是常数；

②对任意的正整数n，当n≥2时，都有2bn=bn-1+bn+1

得出上述等价结论后引导学生思考如何利用这些结论，特别可提醒学生从特殊与一般的关系考虑问题，此时会有学生恍然大悟：b1、b2、b3成等差数列！

于是我们可以从b1、b2、b3成等差数列这一特殊结论求得t的值，但应提醒学生注意的是通过这种方式求得的t的值只能保证b1、b2、b3成等差数列，不能确保{bn}成等差数列.进一步引导学生思考，为避免这种“低级错误”，我们还需要做什么？在这样一步一步的引导下，大多数学生是能够完成第二个小问题的.下面给出(2)的另一种解法：

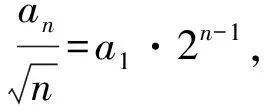
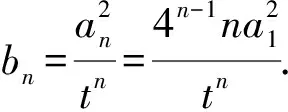
因为{bn}是等差数列，

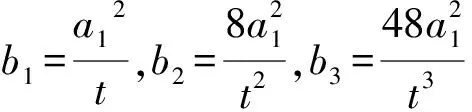
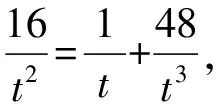
求得t=4或t=12.

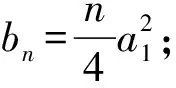
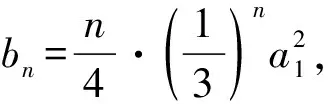
所以数列{bn}是等差数列时，t=4.

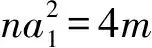
因为n,m都是正整数，a1是整数，

若a1是偶数，设a1=2k，则存在正整数m=nk2；

综上所述,满足条件的所有整数a1的值是一切偶数.

由这个案例可知,导问式解题教学是一种基于问题式的解题教学形式，是“以问题为载体、以教师为主导、以学生为主体”为主要特点的师生互动式的学习方式，在这样的教学中师生双方都是学习和研究的行为主体，它是能达到师生共同进步的教学形式，但是在日常的课堂观察中我们发现在实施导问式解题教学中存在一些误区，主要表现形式有：

1. 导而不问

这是最常见的表现形式，特别是毕业班复习课中表现得更为突出．一些教师在分析问题时往往只注重“由什么知什么”的综合性思维，尽管思路看似很清晰，但没有问题作铺垫，学生“只知其然不知其所以然”，其最终结果是只教会了学生解题(更确切地说是教会了学生解熟悉的题)，而对“如何思考?如何寻找问题解决出路?如何设计解决问题的方案？”等问题没有引起相应的重视．

2．问而不导

与“导而不问”恰恰相反的另一种误区便是“问而不导”，实际表现为看似以问题为导向，但是问题的设置却并不合理，有些问题过于简单无需多问，而有些问题过于繁难学生很难回答，更有甚者,有些问题与教学内容没有必然的因果关系. 此外，还有一种情况是课堂上提问频繁、所提问题过多．曾听过一节高二数学习题课，45分钟的数学课教师共提了大大小小30多个问题，试想要让学生在45分钟时间完成30多个问题的解决，其问题质量能得到保证吗？

3．课堂引入有导有问但教学过程导问缺失

有些教师认为导问式课堂只是在教学引入时使用，他们把“导问式教学”与“问题引入”混为一谈，认为在教学导入过程中使用了问题式引导便是导问式教学，其实导问式教学过程中强调“导问贯穿在包括概念引入、定义讲解、问题解决等在内的教学过程的方方面面，而不是指单纯的教学引入”.

4．问题提出教师有余而学生不足

导问式解题教学过程中问题提出的主体不只是教师更是指学生，很多教师由于理解有误而忽视了学生问题意识的培养，其实，导问式教学的主要标志是“变‘师问生答’为‘生问师导’”，因此，在导问式教学中教师的主要职责不是提出问题而是引导学生提出问题，通过教师的示范引领培养学生问题意识和创新能力.

为避免解题教学过程中出现诸如以上所列的各种误区，在实施导问式解题教学时遵循如下几个基本原则：

1.适时性原则

著名教育家陶行知先生曾经说过：“发明千千万，起点是一问，智者问的巧，愚者问的笨．”，导问式解题教学突出强调以问题为主线引导学生思考和提出问题，但问题的引导要适时，能够学生独立思考的问题并不需要教师“画蛇添足”，思维要求过高的问题不宜引入教学，只有那些通过一定的思考才能达到预期效果的问题才可为我所用.而且什么时候提出相关问题引导思考要掌握“时候”，只有当学生经过一定思考，问题解决的突破“似有非有”的时候抛出提示性问题或引导学生提出类似问题才能达到较好的教学效果.当然，要掌握好问题引导的“时候”需要教师充分了解学情和教学内容，因此导问式解题教学对教师的要求更高，它与问题解答有着本质的区别.

2.适材性原则

所谓“适材”是指所提的引导问题要适合相应的问题背景和学生实际，引导学生思考时要根据实际问题设计合适的引导线索，同时要根据学生问题解决的实际情况作适当难度的问题引导，使学生的思维达到尽可能积极的状态.

3.双向性原则

导问式教学强调的不仅是教师的问题引导，更主要的是通过教师的问题引导提升学生解决问题的能力，因为一个问题的解决往往需要若干个其它问题的解决，因此导问式解题教学的另一重要任务就是通过教师的示范来引导学生自觉地提出问题，通过导问式教学增强学生的问题意识，提升学生提出问题进一步解决问题的能力，从而培养学生的创新意识.因此，导问式解题教学中的问题主体不仅是教师更是学生.

4.信任性原则

要培养学生的问题意识，提升学生提出问题的能力，就必须充分信任学生.有些教师认为学生提不出有质量的问题，因此教学过程出现了问题提出“包办”的现象，其实这是一种片面的理解．很多心理学家研究证实：几乎每一个学生都是爱提问题的，只是由于经常性地出现所提问题与教师期望的不相一致而没有得到应有的肯定，从而淡化了提问题的欲望，久而久之学生就不想提问题而习惯于解答教师提出的问题.因此，导问式解题教学强调信任：信任学生的能力，信任学生天生是提问题的高手！

5.平等式性原则

导问式解题教学更强调师生之间的平等，只有建立在平等师生关系基础上的教学才能真正实施导问式，试想在一个充满着浓郁“师道尊严”的课堂中学生怎么可能大胆提出自己的问题？怎么可能对教师的讲解提出怀疑？怎么可能对自已理解不了的教材提出质疑？陶行知曾说过：“解放学生的头脑，使他们能想；解放学生的眼睛，使他们能看；解放学生的嘴巴，使他们能谈．”，而要让学生能看、能想、能谈，就必须营造平等的师生关系，为学生的畅所欲言提供较好的“心理安全环境”.