通过变题培养学生对新问题的把控能力
陈后万 方均斌
(1浙江省洞头区第一中学 325700; 2温州大学数学与信息科学学院 325035)
素质教育倡导对学生的能力培养,注重人的潜能开发,其根本在于每一个学生今后的发展和成长.而在教学中,笔者发现很大一部分高三学生虽做了大量的题,但面对一些“陌生的问题”还是无从下手,教师也总是抱怨:这种类型的题学生“曾经做过”,但“换一个面孔后”学生为什么还是束手无策?双方很受挫折.尽管原因很多,笔者认为到高三一轮复习之后,基本功扎实的学生所欠缺不是基本知识点的整理归纳,而是综合应用能力的培养和提高,是对知识的融会贯通.它不是让学生成为一个“解题机器”,而是需要他们具有一定剖析能力、化归水平,需要掌握透过表象抓实质的本领.
那么,在高三课堂教学中如何提高学生面对新问题的把控能力呢?笔者认为在高三复习的后阶段,教师可以通过改编、拼合、集择等变题手段对数学问题进行适度处理,不仅提高学生面对新问题的分析、化归能力,领悟新问题的本质,还可以调动学生的积极性,提高学生猜测原题设计的意图,让师生共同进入一个解题的新领域.当然,变题有很多种方式,下面笔者就谈谈体会最为深刻的三点.
1 改编
我们这里的改编是指:(1)改写原数学问题的条件,使形式更新、内容更丰富;(2)改写原题的结论,使封闭题成为开放题,拓展思维;(3)修改问题的呈现方式(如图形语言、文字语言、符号语言之间的转换,或者题型的修改),这些修改是一种让学生领会编题者意图的一种尝试,也是提高学生驾驭新问题能力的一个举措.



虽然只是由选择题改为填空题,形式不同,却可以说呆萌的变化,得到傲娇的效果.
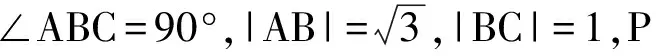
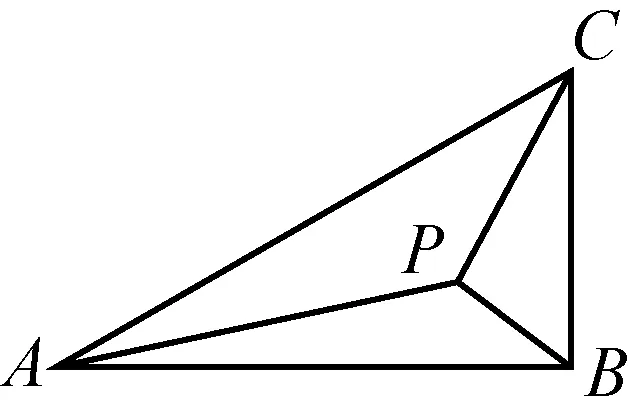
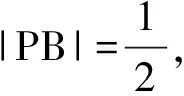
(2)若∠APB=150°,求tan∠PBA.

原题是三角函数问题,根据特殊三角形,运用三角函数和正余弦定理可以解决.原题图形很不错,以三角形为背景,抓住P点的轨迹是圆弧,既有美感又有规律,且原题条件符合极化恒等式的要求.
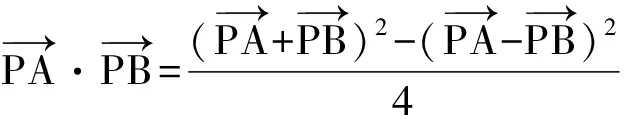
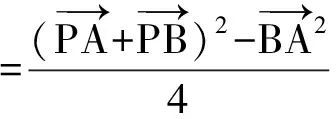
案例3原题(浙江省2006年高考题第10题):f:A={1,2,3}到B={1,2,3}的映射满足f[f(x)]=f(x),这样的函数个数有多少?

原题主要考查映射概念,部分学生可以用例举法求解(数量较少),但容易造成遗漏,分类不完整,思维不严密.笔者将其变化为三个不等式,作为它的条件,相对原题更加突出对排列组合知识的考查,让学生理解并运用排列组合知识.在得出结论f(1)≥f(2)≥f(3)≥f(4)的基础上,运用排列组合知识,分类求出结果.
这样,提高了难度,丰富了原有内容,训练了学生的综合应用能力.其实,不等式只是排列组合的条件和要求,学生必须联系问题,学会深入分析、合理转化,以锻炼学生对新问题的剖析、化归能力,提高透过表象抓住实质的本领.
案例4原题证明不等式
a2+b2+1≥ab+a+b.
改编题删去右边的代数式,改为a2+b2+1≥,在横线上填入代数式,使之恒成立并给出证明.
学生甲:a2+b2+1≥1.

学生丙:a2+b2+1≥ab+a+b.
学生丁:……
这类题起点低,学生可以根据自己不同情况得出不同难度的结论.通过改编,将“封闭题”改为“开放题”,其对学生的思维训练要求显然灵活了!
这样的变题是为了欲擒故纵,先让问题更开放,让学生发散思维、积极联想,再收网寻求解决问题的办法.

通过改编题,可以让学生将原有解法中不足点暴露出来,突显数学问题的本质;可以考查想要考查的重要概念、基本技能、思想方法;通过改编题,可以在知识点之间形成串联、转变,提高学生灵活应用知识以及把控新问题的能力;通过改编题,可以让学生站在更高的高度去思考问题,去猜测设计者的想法及设计意图.
2 拼合
拼合就是对两道或者几道数学问题的解决方法进行串联、并联或者综合,达到从解法少到多解或者从单科知识、技能的考核到多科的能力综合.

这道题考查学生的基本向量知识与不等式最值的结合.
原题2已知a(2,0),b=(x,y),若b与b-a的夹角为300,求|b|的最大值.(《中学教研》2014年第2期高考理科模拟卷)
这道题是比较典型的向量与三角形结合问题,但难度不大.
拼合题已知e1,e2是夹角为1200的两个单位向量,a=4e1+4e2,b·(a-b)=2,求a与b夹角的最大值.
本题拼合的理由是两道题都在向量背景下,分别考查学生应用不等式和解三角形知识 (结合图形).笔者通过拼合,适当改变条件,让其功能更加强大, 条件“b与b-a的夹角为300”改变为b·(a-b)=2,使其原来可以容易作图(向量的夹角),变得似乎无从下手,学生甚至认为只能从代数角度入手.但也不是很容易解决.
略解
b·(a-b)=|b|×|a|×cosθ-|b|2=2,
这里运用了参数分离的想法,并在此基础上运用基本不等式等方法解决.本题若用向量等方法也可以解决,要求的能力更高,若用向量的投影和基本不等式解决,则“含金量”更高.
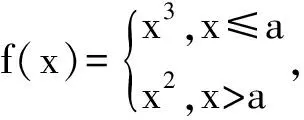
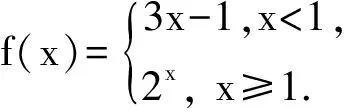
拼合题已知函数f(x)=4x-2x+1,若方程f(f(x))=a有两个实数根,则a的取值范围为.
原题1和2相同之处,都是分段函数,同时都注重学生的数形结合能力,以零点和方程的根为手段.通过拼合变题,转变到对复合函数的考查,突出了复合函数的单调性及定义域问题.对学生的逻辑思维要求更高.表面看似相似的问题,考查的却是学生的不同能力,变换了角度,旧瓶装新酒,以锻炼学生把控新问题的能力.
拼合也是变题,只是另一种手段,一般是拼合两道或者多道数学问题的知识点或解决方法,从更高角度去综合问题,进一步考查学生的能力.通过变换角度,让学生从中寻找差异,求同存异,抓住问题本质,训练学生的分析、归纳能力,善用化归思想,以驾驭新问题.需要注意的是,若综合的知识太多,难度会变大,拼合应该要循序渐进,才有效果.同时在拼合时,不能过于机械,以免出现条件冗余,甚至矛盾的现象.
3 集择
所谓集择就是将若干个常见的数学问题条件集中在一起,要学生根据要求从中选择出几个条件得出一个结论;或者任给一个结论A,要求学生选择其中所给的若干个条件作为条件,由这些条件推出结论A并让学生体验编题的乐趣与艰辛.
案例7[1]问题△ABC中,角A,B,C的对边分别为a,b,c,面积为S,分别给出以下条件:

③a2+b2-c2=4S;
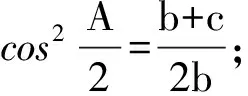
⑥cos2C+cos2B-cos2A=1-2sinBsinC;
⑦(a2+b2)sin(A-B)=(a2-b2)sin(A+B);


能否从中选择三个条件或者自编条件,确定三角形?并求解剩余的元素?
该问题设计新颖,活跃了学生思维,活跃了课堂.一个问题既可以以点带面,也可以四通八达,联系各方面知识.如此变题,改变了以往学生拿一题做一题的习惯,要求学生自己去编题,去审视每个知识,这需要很强的理解能力和驾驭能力.对他们来说是一种全新挑战.
集择是一种很好的提高应对新问题的锻炼方法,一则是学生必须透过一些表面的条件,抓住各条件隐含的本质内容;二是它使学生必须自己架构问题,包括一些错误和不合理的想法,统统都要自己想办法去否定、排除,充分提高了学生的分析和应对能力.
案例8复习回顾已经学过的空间中垂直的结论有哪些?请梳理一下,已知a,b,l是不同的直线,α,β是不重合的平面,从下列几个条件中,选择一些条件作为命题的主要条件和结论,构造正确命题:
①l⊥a,②l⊥b,③b∥a,④b⊥α,⑤a⊥α,
⑥a⊥β,⑦b⊥α,⑧l⊥α,⑨α∥β,⑩α⊥β.
通过这一集择,可以把垂直的知识框架整理出来:线线平行→线面垂直;面面平行→线面垂直;线面垂直→面面平行,等等.本案例把知识的复习变成一道题,让学生从众多的选支中梳理出相关结论,改变了常规一问一答式的复习方法.
集择方法能让学生体会如何去编题,对知识点的把握要求更加全面、更有高度,更能准确联系各个条件;集择方法还能够提高学生的分析能力、联想能力,体会到解题、编题的乐趣.
数学问题的变题方法很多,我们就改编、拼合、集择谈几点想法.我们认为,学生甚至是老师陷入题海的根本原因是没有对数学问题进行总结与变化,致使“解一题抛一题的现象”严重,而且我们还发现,很多老师对一道数学问题解法进行总结的比较多,而对数学问题的结构剖析、问题来源、问题变化等进行总结探索的比较少,这或许也是我国目前数学问题教学的一个“软肋”.笔者长期的教学实践体会是,要把数学问题的变化经常呈现给学生(至于问题解决之前还是之后,需要看具体的情况),不要隐去问题的来源,否则会让学生被千变万化的表面形式所迷惑.有时还需要和学生“一起变题”或者引导他们与命题者进行“心灵上的对话”.只要长期坚持,一定会让学生“以不变应万变”,提升应对数学问题新面孔的能力.

