气液两相流管道泄漏瞬态模型及数值计算

蔡永桥，卢 进，王 庆，孙晓阳，曹学文

1.中海油能源发展装备技术有限公司，天津 300459

2.中海油山东化学工程有限责任公司，山东济南 250014

3.中国石油大学（华东）储运与建筑工程学院，山东青岛 266580

气液两相流管道泄漏瞬态模型及数值计算

蔡永桥1，卢 进1，王 庆2，孙晓阳3，曹学文3

1.中海油能源发展装备技术有限公司，天津 300459

2.中海油山东化学工程有限责任公司，山东济南 250014

3.中国石油大学（华东）储运与建筑工程学院，山东青岛 266580

气液两相流管道一旦有泄漏发生，管道压力、截面含液率及流速等参数均会发生改变，分析泄漏过程中气液两相流的瞬态变化对于探究管道泄漏特征、实施两相流管道泄漏检测与定位具有重要意义。对气液两相流泄漏过程进行瞬态分析，在双流体模型的基础上建立气液两相流泄漏系统数学模型，利用隐式差分法求解控制方程，并用C++编程计算气液两相流泄漏数值解，分析分层流条件下泄漏对管道压力、截面含液率、气液相流速等参数的影响，将数值计算结果与气液两相流泄漏实验数据进行对比。结果表明：管道泄漏后，泄漏点下游管道压力、截面含液率、气液相流速等参数值均下降，且数值计算结果与实验数据趋势一致，证明所建立的泄漏模型适用性较好。

气液两相流；分层流；泄漏模型；数值计算；实验研究

油气混输管道作为一种高效、安全、经济、环保的运输手段，在石油、天然气等能源运输中发挥着重要的作用。到目前为止，油气多相流混输管道已成为国内外海底管道的主要运输方式。管道泄漏问题一直是管道安全生产维护领域的难题，且事故发生率较高，老化、腐蚀、磨损、焊接缺陷、设计缺陷、运行超过设计极限及故意破坏等多种原因，都会导致管道的泄漏，进而造成严重的后果[1-2]。在油气混输管道的运行管理中，及时检测到管道泄漏并定位，是管道安全运行的必要前提[3]。气液两相流管道流型多，流动参数之间的关系复杂，一旦有泄漏发生，其压力、持液率、介质流速等参数值发生改变，影响泄漏检测的精度及灵敏度。因此建立气液两相流泄漏系统数学模型，分析泄漏过程中气液两相流的瞬态变化，对于探究管道泄漏特征、实施两相流管道泄漏检测与定位具有重要意义。

本文在双流体模型的连续性方程和动量方程的基础上引入泄漏方程，并结合分层流的结构方程，建立分层流条件下气液两相流泄漏系统数学模型，并利用隐式差分法对模型进行求解，给出水平管道气液两相分层流动稳态及泄漏工况的计算方法。利用C++编程求解分层流泄漏偏微分方程组，得到管道泄漏后压力、持液率等流动参数的变化规律，为气液两相流管道泄漏研究提供参考。

1 模型建立

1.1 假设条件

管道作为一个水力系统，沿线任一点发生泄漏都会引起该点流动参数的变化，破坏管道的流动状态，该瞬变波动从泄漏点沿管道向上下游传播，使整条管道进入瞬变流动状态[4]。在气液两相双流体模型的基础上，以流体力学基本守恒方程为基础，引入泄漏方程，并结合气液分层流的结构计算式，建立气液分层流泄漏瞬态方程组[5-9]。针对分层流管道输送的特点以及前人所作的研究成果，提出如下假设[10]：

（1）管道内气相介质为理想气体。

（2）管道内气液两相处于热力学平衡状态，忽略相变与相间传质。

（3）管道内介质流动过程中温度保持不变，采用等温一维模型，忽略能量方程。

（4）沿管道横截面上，气液两相压力、流速、密度等各流动参数在各相所占的平面内均匀分布。

1.2 数学模型

基于所作的假设，可以得到水平管路中气液两相流动的基本方程如下：

（1）连续性方程。

根据气液介质各自的流量守恒关系，气相和液相的连续性方程分别为：

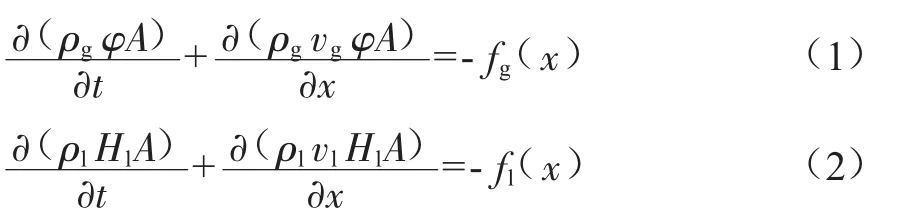
式中：ρg、ρl分别为气、液相密度，kg/m3；φ为截面含气率即气相流通面积与管路总流通面积之比，%；Hl为截面含液率即液相流通面积与管路总流通面积之比，%；A为管道截面积，m2；t为时间，s；vg、vl分别为气、液相速度，m/s；x为管道轴向坐标，m；fg（x）、fl（x）分别为x位置处的气、液相泄漏质量，kg。

（2）动量守恒方程。

气、液相动量守恒方程分别为：

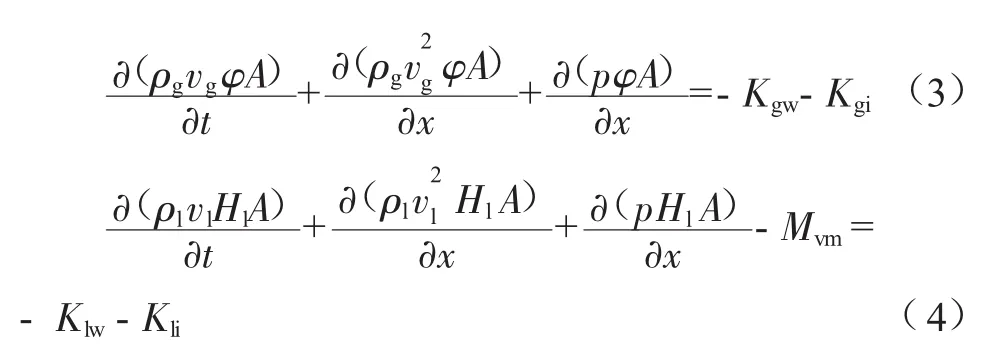
式中：p为管道内压力值，MPa；Kgw、Klw分别为单位长度气、液相与管壁间的剪切力，N/m；Kgi、Kli分别为单位长度气相侧与液相侧受到的相间剪切力，N/m；Mvm为单位长度相间虚拟质量力，N/m，分层流中通常为0。

（3）密度方程。

流体密度是压力的函数，假定管道横截面上气液两相压力相同，p=pg=pl，由理想气体状态方程可知，气相密度为：

式中：Z为气体压缩因子；R为气体常数，J/（mol·K）；T为气体温度，K；cg为气体中的声速，m/s。

（4） 泄漏方程[11-12]。

参照节流喷嘴流量公式，以泄漏点处管内外压差为基础，引入泄漏参数Fk，从而计算泄漏混合介质质量。Fk为经验常数，取值与泄漏尺寸、泄漏位置及持液率有关，应根据现场数据或实验数值拟合取得。在此基础上，引入狄克拉分布函数δ计算泄漏对于管道不同位置流体各参数的影响，有：

式中：f*为泄漏质量，kg；ρ*为泄漏点气液混合物密度，kg/m3；p*为泄漏点处管道内压力，MPa；pamb*为泄漏点处管道外压力，架空管道则为大气压力，水下管道则为该水深处的静水压力，MPa；ε*为泄漏气体的体积分数，%；x*为泄漏点位置，m。

δ为狄克拉分布，在除了零以外的点，其函数值等于零，而其在整个定义域上的积分等于1，用数学式表示为[13]：

如果函数的非零值是在自变量为x*时取得的，可用变形的狄克拉分布表示管道上有一点发生泄漏，而管道其他位置完好。具体表示为：

（5）分层流结构方程。

本文的研究对象为气液分层流流动，分层流气液相分布如图1所示，在重力作用下，液相位于管道底部，气相位于管道顶部，两相之间有明显的分界面，气液界面采用FLAT模型[14]。

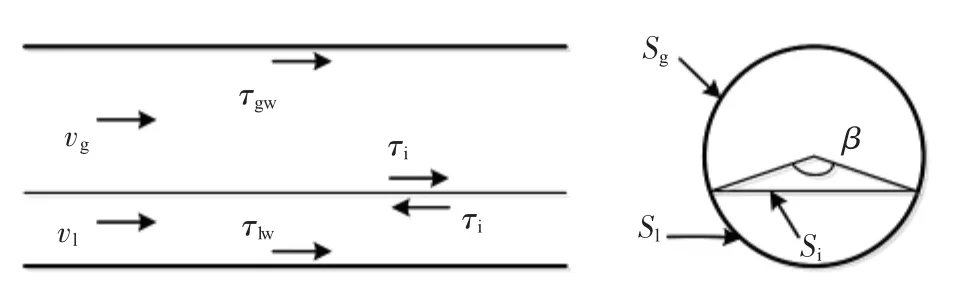
图1 分层流气液相分布

气相与管壁间的剪切力为：

液相与管壁间的剪切力为：

相间剪切力：

式中各物理量的求解方法可参考文献[14]。

以上建立起了分层流条件下气液两相管道泄漏瞬态分析方程组，结合管道泄漏相应的边界条件，描述泄漏瞬变过程中各参数的变化情况。

1.3 方程求解

对管道处于正常运行和发生泄漏状态分别进行求解，其边界条件以实验室环道参数条件为基础，给定管道入口气液流量及入口压力，流体泄漏过程中泄漏点处背压为恒定值，即外界大气压pamb。

采用隐式差分法对控制方程偏微分方程组进行求解。用网格化方法[15]处理变量管长x和时间t，管道差分网格如图2所示，则由隐式差分法可以得到偏微分方程式（1）至式（4）的差分方程。

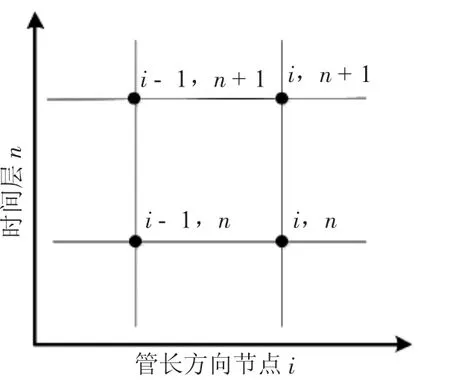
图2 管道差分网格示意

气体连续性方程离散为：

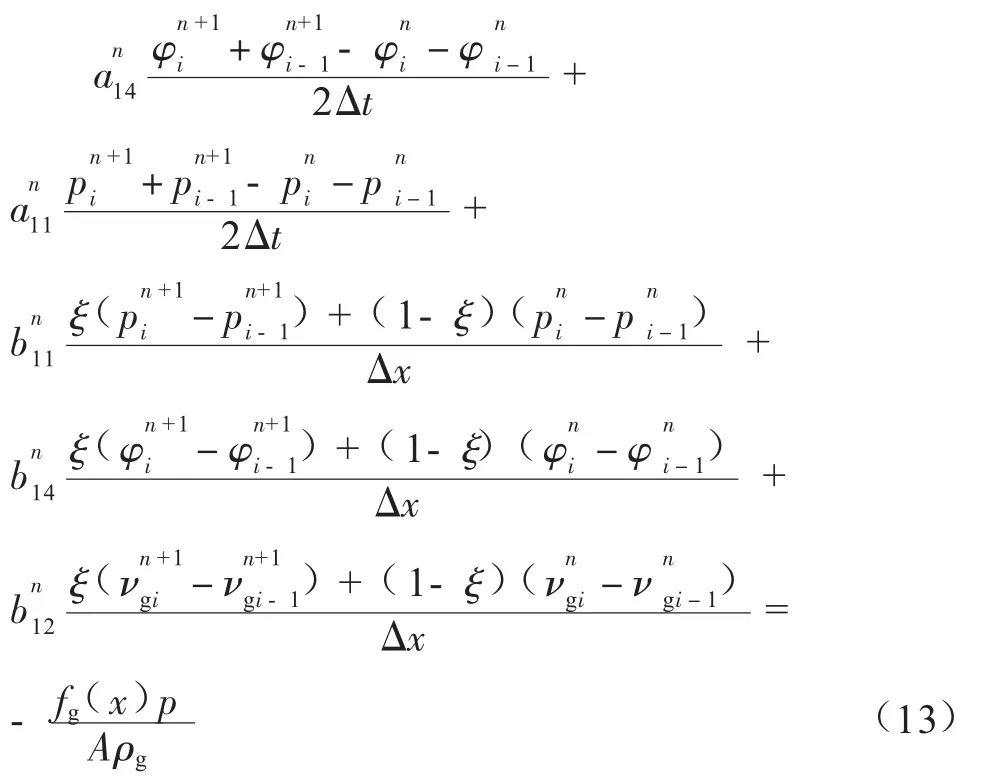
式中：ajk、bjk分别代表对t和x进行微分处理，其中下标j=1，2，3，4分别对应气相连续性方程、液相连续性方程、气相动量方程以及液相动量方程，下标k=1，2，3，4 分别对应参数p、φ、vg、vl；为（ i，n）节点处的截面含气率，%；为（i，n） 节点处的压力值，MPa；为（i，n） 节点处的气相速度，m/s；ξ为加权系数；△t为时间步长，s；△x为距离步长，m。

同理，可分别写出液相连续性方程及气、液相动量方程的离散格式。

液相连续性方程：

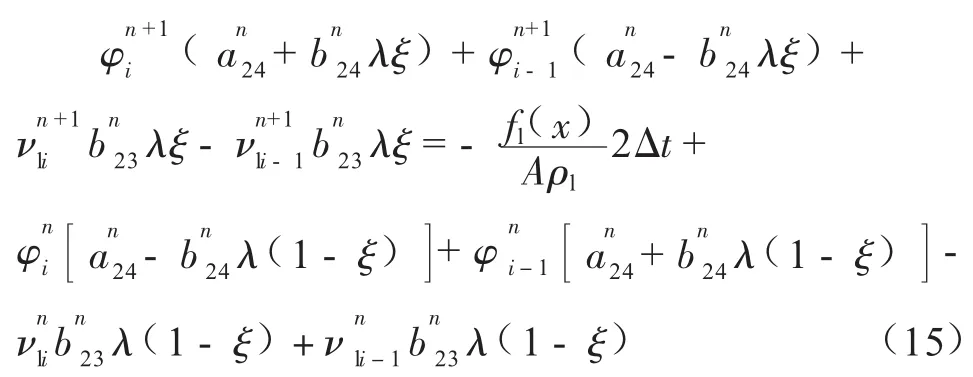
气相动量方程：

液相动量方程：

式（14）至式（17）为计算管道压力、气液相流速及含气率的差分方程。瞬态方程的求解过程为：

（1）给定管道距离步长与时间步长。

（2）给定管道入口气、液相流量及入口压力值，求解管道稳定运行时各管段剖分面上的运行参数值。

（3）指定泄漏位置，将该位置管道压力值代入式（6）计算泄漏量。

（4） 由0时间层的参数代入式（14）至式（17），求出初始时刻各流动参数值。

（5）重复步骤（3）～（4），直到时间层为指定时间。

2 计算结果

2.1 计算工况

以实验室管道基础数据为初始条件，利用C++进行编程计算。图3为气液两相流实验环道的流程示意图，实验介质为空气和水，实验环道采用不锈钢管焊接而成，在环道的实验段上有4段透明有机玻璃管，长约2 m，以便观察多相流在管道中的流型。管道长40 m，分为DN50、DN80两种管径管段，管道入口处气、液相流量分别为15.6 m3/h、0.9 m3/h，管道入口压力为1.3 MPa。计算的距离步长与时间步长分别取0.5 m、0.1 s。根据实验室环道情况，取泄漏点为距管道入口12 m处。

图3 实验环道示意

多相流实验环道实物如图4所示。多相流部分实验装置主要包括：气液相介质供应系统、流量调节装置、气液相分离系统、实验测试管段、储液装置以及控制系统；泄漏部分实验装置包括：信号采集传感器、泄漏口模拟系统、信号采集与处理系统。环道沿程设置了温度、压力、流型等测量点，利用LabView编程采集实验管路起点的气液流量、温度、管道沿线压力。

图4 多相流实验环道实物照

沿程采用4个MPM480型压力传感器，量程0～400 kPa，精度为0.25%。压力传感器及泄漏点（DN80、DN50两部分管段上分别各设置一处泄漏点）位置见表1。由于泄漏点的周向位置对于分层流的泄漏规律有很大影响，故将每个泄漏点又分为上泄漏口和下泄漏口。用球阀连接孔板法兰的装置模拟泄漏系统，快速打开球阀模拟管道发生泄漏，通过更换不同尺寸的孔板，调节泄漏孔口直径。模拟泄漏系统实物及其结构如图5所示。

表1 传感器（P1～P4） 及漏点位置

2.2 管道参数变化

管道沿程压力、持液率及气、液相介质流速的数值仿真计算结果如下：

（1）管道沿程压力的变化。由图6可知，管道发生泄漏后，部分流体流出管道，引起管内流体局部密度减小，故泄漏点压力迅速降低。在实验室条件下，两相流实验环道入口压力由压缩机控制，故在数值模拟中，管道发生泄漏后泄漏点上游压力几乎无变化；而在实际事故中，这种压力降低的趋势应以压力波的形式迅速向管道上下游传递，导致管道沿线压力值均降低。管道压力的变化仅在泄漏发生后2 s内变化明显，之后管道维持在一个低于管道正常操作压力的稳定压力值运行。

（2）管道沿程截面含液率的变化。当管道发生泄漏，尤其是较小泄漏的情况，截面含液率的变化对泄漏检测尤为重要。截面含液率的变化越大，造成的管道局部压降就越大。Stuart等人[16]的研究表明，对于分层流的泄漏检测依赖于对截面含液率的分析。由图7可知，泄漏导致泄漏点处截面含液率迅速下降。截面含液率下降的趋势仅对泄漏点下游产生影响，对管道上游几乎无影响，沿程数值基本一致。这是由于在流体流型为分层流的条件下，位于管道底部的泄漏点导致管道泄漏的流体主要是液相，故截面含液率不断降低。

图5 漏点处实物照及其结构

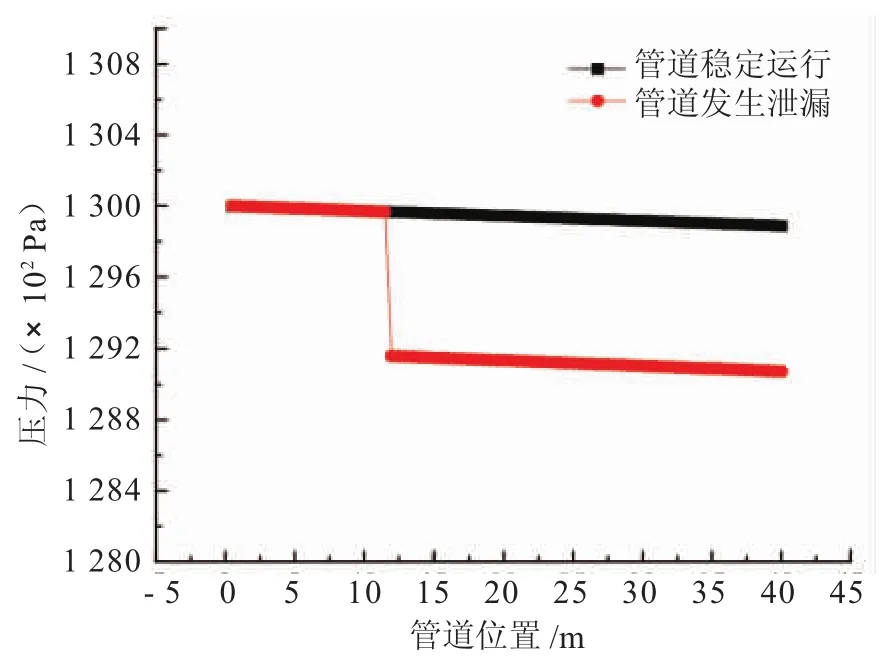
图6 数值模拟管道稳定运行与泄漏后沿程压力

（3）管道沿程气相介质流速的变化。由图8可知，管道发生泄漏后，管道下游气体介质流速迅速降低。当管道正常运行时气相的流速为2.207 m/s，泄漏发生瞬间泄漏点气相流速降低至2.202 m/s。这是由于气体在管道内的流速与管道压力有关，泄漏后管道压力降低，故气体流速下降明显。另外由于假设管道发生泄漏时泄漏点位于管道下部，流出的流体全部为液体，泄漏后管道持液率降低，气相流通面积变大，进口流量恒定，故泄漏点下游气相流速降低。由于管道入口处流量固定，所以泄漏点上游流速基本不变。

图7 数值模拟管道稳定运行与泄漏后管道截面含液率变化

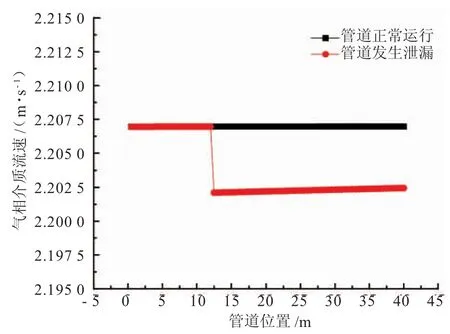
图8 数值模拟管道稳定运行与泄漏后气相流速变化

（4）管道沿程液相介质流速的变化。由图9可知，管道正常运行时，管内为分层流流动，液体流速较低，为0.127 m/s；管道发生泄漏后，泄漏的介质全部为液体，管道下游液体介质流速迅速降低至0.122 m/s。

2.3 数值计算与实验数据对比

管道发生泄漏后，管道末端压力略有降低。将实验采集到的管道出口压力信号变化值与数值模拟计算压力值进行对比，见图10。由于实验用压力传感器精度较差，故对实验数据与数值计算数据均做了归一化处理，将压力值转化为无量纲的压力幅值数据，然后进行比较。

图9 数值模拟管道稳定运行与泄漏后液相流速变化

图10 管道末端压力幅值的数值模拟与实验数据对比

从图10中可以看出，数值计算结果与实验数据变化趋势吻合。实验中，管道正常运行25 s后打开泄漏阀门，流体从管道下部泄漏孔流出，泄漏约20 s后关闭阀门，管道恢复正常运行。泄漏导致管道压力迅速降低，上游介质流量补充导致压力突降后迅速增大，之后在一个略低于正常运行时的压力值上下波动。因实验环道管道长度较短，且管内压力较低，所以发生泄漏后，压力减低不明显，但从图10中可以看出泄漏发生后压力有下降的趋势，停止泄漏后管道压力恢复到正常值。

3 结论

（1）利用C++编程求解分层流泄漏偏微分方程组，得到管道泄漏后压力、持液率等流动参数的变化规律，管道发生泄漏后，泄漏点下游压力迅速降低，持液率迅速降低，气、液相流速均降低；管道上游流动参数影响较小。

（2）数值模拟结果与实验数据吻合较好，对比数值模拟结果与实验数据可知，泄漏发生后管道末端压力略有下降，停止泄漏后管道压力恢复到正常值。

[1]吴世来.输气管道泄漏音波检测信号处理的研究[D].沈阳：沈阳工业大学，2007.

[2]余洋.中国油气管道发展现状及前景展望[J].国际石油经济，2007，15（3）：28-33.

[3]刘涛.管道检测系统中的信号处理技术研究[D].天津：天津大学，2007.

[4]李玉星，冯叔初.湿天然气管输瞬变流模型及数值模拟技术研究[J].油气储运，1998，17（5）：11-17.

[5]韩炜.管道气液两相流动技术研究[D].成都：西南石油学院，2014.

[6]孔祥伟，林元华，何龙，等.一种考虑虚拟质量力的两相压力波速经验模型[J].力学季刊，2015（4）：611-617.

[7]江延明，李玉星，冯叔初.气液两相流瞬变流数值模拟研究[J].油气储运，2005，24（11）：22-27.

[8]陈家琅，陈涛平.石油气液两相管流[M].2版.北京：石油工业出版社，2010：17-20.

[9]李玉星，冯叔初.湿天然气管输瞬变流模型及数值模拟技术研究[J].油气储运，1998，17（5）：11-17.

[10]王文光，颜慧慧，曲兆光，等.起伏湿气管路持液率和压降计算模型[J].石油工程建设，2016，42（6）：1-4.

[11]BUENO D E G P，FIGUEIREDO A B，BAPTISTA R M，et al.Numerical simulation of stratified two-phase flow in a nearly gas-liquid pipeline with a leak[C]//Calgary：International Pipeline Conference.Calgary，Canada：[s.n.]，2014：1-4.

[12]王明新.数学物理方法[M].北京：清华大学出版社，2013：81-87.

[13]TAITELY，DUKLERAE.A model for predicting flow regime transition in horizontal and near horizontal gas-liquid flow[J].Aiche J.，1976，22（1）：47-55.

[14]XIAO J J，SHONHAM O，BRILL J P.A comprehensive mechanistic model for two-phase flow in pipelines[C]//SPE Annual Technical Conference and Exhibition.[S.l.]：Society of Petroleum Engineers，1990.

[15]HODNE K.Leak detection in two-phase oil and gas pipelines by parameter and state estimation[J].Institutt for Teknisk Kybernetikk，2008.

[16]DR.STUARTLSCOTT，DR.MARIAABARRUFET.Worldwide assessment of industry leak detection capabilities for single&multiphase pipelines（Project Report Prepared forthe Minerals Management Service Under the MMS/OTRC Cooperative Research Agreement）[R].35-01-99-CA-31003，2003.

Transient model and numerical calculation of gas-liquid two-phase flow pipeline leakage

CAIYongqiao1，LU Jin1，WANG Qing2，SUN Xiaoyang3，CAO Xuewen3
1.CNOOC Energy Development Equipment Technology Co.，Ltd.，Tianjin 300459，China
2.CNOOC Shandong ChemicalEngineering Co.，Ltd.，Jinan 250014，China
3.College of Pipeline and CivilEngineering，China University of Petroleum （Huadong），Qingdao 266580，China

There are many flow patterns in gas-liquid two-phase flow pipelines，and the relationship between flow parameters which would change once pipeline leakage happens is complicated.Analyzing the transient process of leakage is important to implement leakage detecting and locating of gas-liquid two-phase flow pipeline.A mathematical model of leakage system for gas-liquid pipeline is established and the leakage characteristics including pressure，liquid holdup，gas velocity and liquid velocity in stratified flow condition are analyzed.The control equations are solved by implicit difference method，and the leakage numerical solution of gas-liquid two-phase flow is calculated by C++programming.The solution shows that the pressure，liquid content rate in cross-section，velocities of gas and liquid at downstream of pipeline leakage point all drop as the leakage occurs.And the numerical results are in good agreement with the experimental data，proving that the established leakage modelhas a wellapplicability.

gas-liquid two-phase flow；stratified flow；leakage model；numericalcalculation；experimentalresearch

10.3969/j.issn.1001-2206.2017.06.006

蔡永桥（1983-），男，四川南充人，工程师，2007年毕业于西南石油大学过程装备与控制工程专业，工程硕士，现主要从事管道智能检测及管道完整性管理技术服务专业的研究工作。Email：caiyq3@cnooc.com.cn

2017-06-30