Parameter Estimation of Lindley Distribution Under Type Ⅱ Censored Samples
LONG Bing
(School of Mathematics and Physics, Jingchu University of Technology, Jingmen 448000, China)
Parameter Estimation of Lindley Distribution Under Type Ⅱ Censored Samples
LONG Bing
(School of Mathematics and Physics, Jingchu University of Technology, Jingmen 448000, China)
Maximum likelihood estimation of the parameter from the Lindley distribution was discussed under Ⅱ censored data. The interval estimation and inverse moment estimation were given, and the random simulation method was used to analyze the parameter. An example was provided to find out the two kinds of point estimation and interval estimation about the parameter under different type Ⅱ censored samples.Comparison between the two point estimations was discussed.
Lindley distribution; Chi-quare distribution; interval estimation; inverse moment estimation; maximum likelihood estimation
Lindley distribution was proposed by Lindley in the literature[1-2] in 1958, which is an important distribution in reliability study. For some life data, the use of Lindley distribution model to fit the effect will be better. At present, there are a lot of statistical scholars who have discussed its properties, and obtained a lot of research results. The properties and applications of compound Lindley distribution were studied in the literatures [3-5]. The empirical Bayes one-sided test was discussed in the literature [6] in the case of independent identically distributed sample. The EB test function was constructed by using the recursive kernel estimation of density function. The optimality of the test function was proved, and the convergence rate was obtained. The empirical Bayes test function of the parameter from Lindley distribution was discussed based on NA random sample sequence in the literature [7]. The interval estimation and hypothesis testing of the parameter in Lindley distribution were studied in the full sample in the literature [8]. The failure model of incomplete data with Lindley distribution was discussed in the literature[9],and maximum likelihood estimation method was used to obtain point estimation and asymptotic confidence interval estimation of the model. An example was given to show that the Lindley distribution have better adaptability compared with exponential distribution and Weibull distribution.
In this paper, we will discuss the maximum likelihood estimation, interval estimation and inverse moment estimation of the parameter from Lindley distribution in Ⅱ censored samples, the parameter will be estimated by the method of stochastic simulation, and the average deviation will be calculated. Finally, an example will be given to illustrate the feasibility of the proposed method.
The probability density function of Lindley distribution is
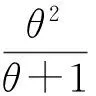
(1)
Its distribution function is
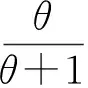
(2)
with parameterθ>0.
1 Maximum likelihood estimation of the parameter
The data in life test for some data will usually be censored, leading to incomplete data, namely, censored way are type I censored, type Ⅱ censored and so on.
It is assumed that there arenproducts that are independent of each other and are subject to Lindley distribution, with type Ⅱ censored test. When observed withmfailure samples, the remainingn-msamples have been withdrawn from the test. The failure time of themsamples have been observed to meetX(1)≤X(2)≤…≤X(m). For the sake of convenience, we will omit the parenthesis of the subscript numbers. TheXirepresents the minimumiobservation value, which is the full sample case whenm=n.
According to the above test, the likelihood function is
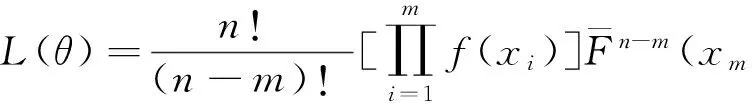
(3)
Substituting (1) and (2) to (3) gives
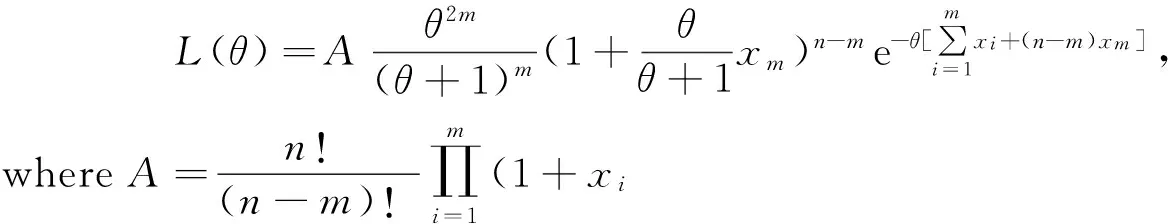
Log likelihood function is
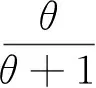

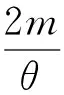
Obviouslyh1(θ)>0,h2(θ)>0. Whenθ→0+,h1(θ)>h2(θ)
So,h1(θ) is strictly monotone decreasing lower convex function on (0,+∞) and
Therefore,h2(θ) is also strictly monotone decreasing lower convex function on (0,+∞),andh1(θ) (4) According to the distribution function of Lindley distribution, we can get the following lemma. Proof:LetFX(x),FY(y) denote the distribution function of random variableXandY, respectively, then The above expression is just the distribution function of standard exponential distribution, proving Lemma 1. According to the above test, letX(1),X(2),…,X(m)be a type Ⅱ censored sample from Lindley distribution (2) with a capacity ofn. One can obtain from Lemma 1 that is a type Ⅱ censored sample from standard exponentialy distribution (2) with a capacity ofn. Set up …… According to literature [10],W1,W2,…,Wmare independent and identically distributed and follow standard exponential distribution. Proof: BecauseWj,j=1,2,…,mfollows standard exponential distribution, its characteristic function is The above formula is the characteristic function of the Chi-square variable with 2mdegree of freedom. Lemma 2 is proved by the unique decision of characteristic function and the distribution of random variable. It can be proved thatWj,j=1,2,…,mis a monotonically increasing function ofθ, soSmis a monotonically increasing function ofθ. Theorem1LetX(1),X(2),…,X(m)be a type Ⅱ censored sample from Lindley distribution (2) with a capacity ofn, for any 0<α<1, under the confidence level of 1-α,the confidence interval ofθis BecauseW1,W2,…,Wmare independent and identically distributed and follow standard exponential distribution, it can be used as a quasi sample. Thus, inverse moment estimation of the parameterθis determined by the following expression (5) Setθ=1. A simple random sample is randomly generated with a capacity ofnfrom Lindley distribution (2). Differentmvalues are used to obtain type Ⅱ censored samples. Maximum likelihood estimation and inverse moment estimation of the parameterθcan be obtained by expressions (4) and (5). Repeat the above process 1 000 times to obtain the mean and relative deviation of the parameter estimations. The simulation results are shown in Table 1. Tab.1 Results of stochastic simulation The simulation results show that the deviation of inverse moment estimation is smaller than maximum likelihood estimation in small sample case, with the increase of sample size, the deviation of inverse moment estimation is larger than maximum likelihood estimation. In general, the mean of inverse moment estimation is larger than maximum likelihood estimation, therefore, the inverse moment estimation is more effective in small sample situations. Setθ=1, a simple random sample is generated with a capacity of 20 from Lindley distribution (2) as follows 0.111 8,0.291 5, 0.327 9, 0.394 8, 0.531 5, 0.628 4, 0.779 1, 0.848 4, 0.939 5, 1.332 3, 1.475 2, 1.719 0, 1.862 5, 1.900 4, 2.061 6, 2.098 8, 3.130 7, 3.303 7, 4.295 6, 6.593 2. Differentmvalues are used to obtain different type Ⅱ censored samples, and carried on the statistical analysis. The results are listed in Table 2. Tab.2 Results of statistical analysis (α=0.1) We can see from Table 2 that when sample sizenis fixed, the interval length increases with the decrease ofm. Inverse moment estimation is closer to the true value than maximum likelihood estimation. [1] LINDLEY D. Introduction to probability and statistics from a Bayesian viewpoint, part II: inference[M]. Cambridge: Cambridge University Press, 1965. [2] LINDLEY D. Fiducial distributions and Bayes’ theorem[J].J Royal Stat Soc, 1958,20(1):102-107. [3] GHITANY M E, ATIEH B, NADARAJAH S. Lindley distribution and its application[J]. Math Comput Simula, 2008,78(4):493-506. [4] GHITANY M E, ALMDK, NADARAJAH S. Zero-truncated Poisson-Lindley distribution and its application[J]. Math Comput Simula, 2008,79(3):279-287. [5] ZAMANI H, ISMAIL N. Negative binomial-Lindley distribution and its application[J].J Math Stat, 2010,6(1):4-9. [6] 杜伟娟,彭家龙,李体政.Lindley分布参数的经验Bayes检验的收敛速度[J].统计与决策,2012,21:23-26. [7] 范梓淼,周菊玲. NA 样本下Lindley 分布参数的经验Bayes 检验[J].贵州大学学报(自然科学版),2016,34(2):68-70. [8] 龙 兵. Lindley分布中参数的区间估计和假设检验[J].广西民族大学学报(自然科学版),2014,20(1):59-62. [9] 黄文平,周经伦,宁菊红,等.基于竞争失效数据的Lindley分布参数估计[J].系统工程与电子技术,2016,38(2):464-469. [10] LAWLESS J F. Statistical models and methods for lifetime data[M].New York: Wiley, 2003. 2017-03-31 国家自然科学基金资助项目 (61374080)*通讯作者,E-mail:qh-longbing@163.com O212.2 A 1000-2537(2017)06-0071-05 Ⅱ型删失下Lindley分布的参数估计 龙 兵* (荆楚理工学院数理学院,中国 荆门 448000) 在Ⅱ型删失数据下,讨论了Lindley分布参数的最大似然估计.给出了参数的区间估计和逆矩估计,运用随机模拟的方法对参数进行了统计分析.通过一个例子求出了在不同Ⅱ型删失样本下参数的两种点估计及区间估计,并进行了比较. Lindley分布;χ2分布;区间估计;逆矩估计;最大似然估计 10.7612/j.issn.1000-2537.2017.06.012 (编辑 HWJ)
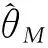
2 Interval estimation and inverse moment estimation of the parameter
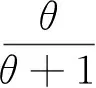
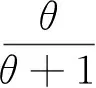
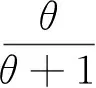
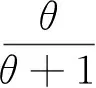
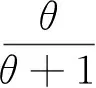
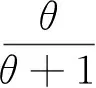
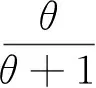
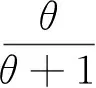
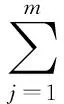
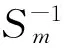
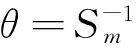
3 Stochastic simulation

4 Example