Pareto分布形状参数的最小风险同变估计

徐 宝，王宇廷，马艺光

(吉林师范大学 数学学院，中国 四平 136000)

Pareto分布形状参数的最小风险同变估计

徐 宝，王宇廷，马艺光

(吉林师范大学 数学学院，中国 四平 136000)

在加权p，q对称损失函数下，对实际中广泛应用的两参数Pareto分布，当刻度参数已知时，用参数估计方法，研究了形状参数的最小风险同变估计的形式和性质. 得到了最小风险同变估计的一般形式，又经由该参数的广义Bayes估计，得到了最小风险同变估计的精确形式，并证明了这一最小风险同变估计具有最小最大性，从而它也是该参数的最小最大估计，由此将Pareto分布形状参数的最小风险同变估计、广义Bayes估计以及最小最大估计联系起来.

Pareto分布；最小风险同变估计；Bayes估计；最小最大估计

Pareto分布是一种在实际中有着广泛应用的统计分布，它一开始是 Pareto 引进作为收入的分布，主要用来描述诸如个人收入、城市人口的容量等问题. 此外，自然现象的发生、股票价格的起伏波动、油田位置、保险风险等也可以用Pareto分布来描述[1]. 本文关注两参数Pareto分布，其定义如下：若连续型随机变量X的概率密度函数为

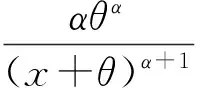
(1)

则称随机变量X服从两参数Pareto分布，其中α为形状参数，θ为刻度参数.

在现代统计文献中，Pareto分布参数的统计推断问题是常见的研究内容. 如：形状参数的极大似然估计和一致最小方差无偏估计[2]；刻度参数的加权矩估计和最好线性无偏估计[3]；在LINEX损失函数下，形状参数的经验Bayes估计[4]；在平方损失函数下，形状参数的渐进最优与可容许的经验Bayes估计及其性质[5]；在平方损失函数和LINEX损失函数下，形状参数和可靠性指标的Bayes估计[6]；刻度参数在右删失数据下的经验Bayes渐进性质[7]；在q-对称熵损失函数下，形状参数的最小风险同变估计、Bayes估计、可容许与不可容许估计以及最小最大估计[8]，广义矩估计[9]，刻度参数的区间估计[10]，形状参数在某些限制下的估计[11]. 这些研究结果极大地丰富了Pareto分布参数估计的内容，但从各种估计之间的关系来研究参数的估计形式和性质的成果却并多不见. 本文将从这一角度出发，在Bayes框架下，研究Pareto分布参数的估计问题. 在加权p,q对称损失函数[12]

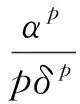
(2)

下，当刻度参数θ已知时，研究Pareto分布形状参数α的最小风险同变估计的一般形式及其性质，然后经由Bayes估计，得到α的最小风险同变估计的精确形式，并证明这一最小风险同变估计同时还具有最小最大性，即它也是α的一个最小最大估计. 在一定程度上将Bayes估计、最小风险同变估计以及最小最大估计联系在一起.

1 形状参数的最小风险同变估计

这一节在损失函数(2)下，对Pareto分布(1)，当刻度参数θ已知时，讨论形状参数α的最小风险同变估计的一般形式与精确形式.

Pareto分布(1)中形状参数α的最小风险同变估计由下面的定理给出.

定理1若X1,X2,…,Xn为抽自Pareto总体(1)的一组容量为n的样本，记为X=(X1,X2,…,Xn)，再记Z=(Z1,Z2,…,Zn)，其中Zi=Xi/Xn,i=1,2,…,n-1，Zn=Xn/|Xn|，当刻度参数θ给定时，假设估计量δ0(X)为形状参数α在损失函数(2)下的同变估计，且具有有限风险，则α的最小风险同变估计具有如下的形式

且在几乎处处相等的意义下，该估计是唯一的，其中E1表示α取1时估计量的数学期望.

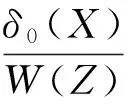
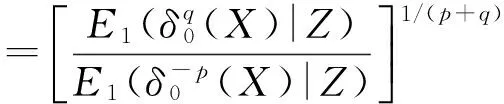
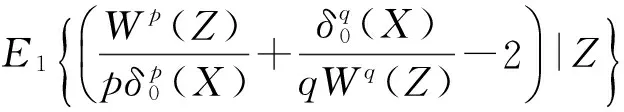
对Pareto分布(1)，若要给出形状参数的α最小风险同变估计的精确形式，则只需预先给定该参数的一个风险有限的同变估计δ0(X)，由定理1.1 的表达式即可完成，但是计算比较麻烦.下面将在Bayes框架下，经由讨论α的Bayes估计，较快捷地得到α的最小风险同变估计的精确形式.

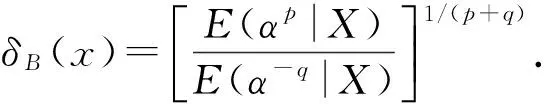
证取参数α的任一估计量δ(X)，则在损失函数(2)下，δ(X)对应的Bayes风险为

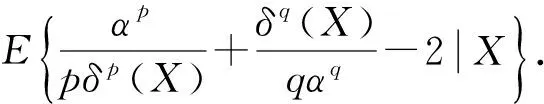
在两种给定先验分布下，参数α的Bayes估计的精确形式由下面推论给出.

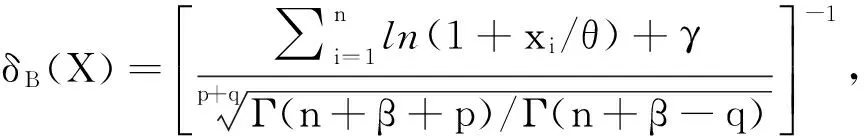
证由于样本X1,X2,…,Xn的联合概率密度函数为

从而参数α的后验密度为

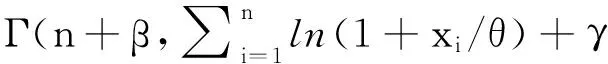
由定理2知，α的Bayes估计为

下面来证明这一Bayes估计是唯一的，为此只需证明δB(X)的Bayes风险有限，即rπ(δB(X))<∞.

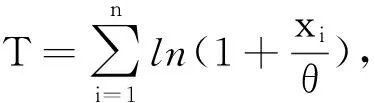
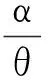
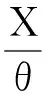
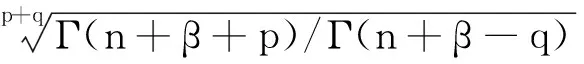
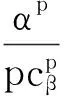
从而δB(X)的Bayes风险为

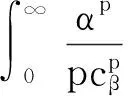
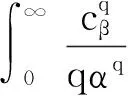
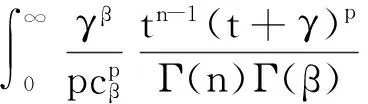
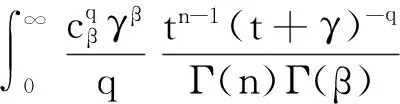
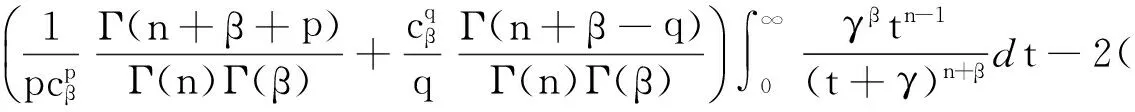
即δB(X)的Bayes风险有限，所以α的Bayes估计δB(X)是唯一的.

推论2在无信息先验分布π(α)=1/α下，参数α的广义Bayes估计的形式为

同时δ*(X)也是α的最小风险同变估计[14].

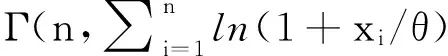
再由文献[11]知，δ*(X)也是α的最小风险同变估计.

2 参数α的最小最大估计

参数α的最小风险同变估计δ*(X)也是它的最小最大估计，为证明这一论断，先介绍如下引理[15].

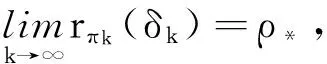
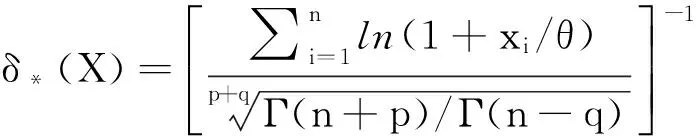
证易知参数α的估计量δ*(X)的风险函数为

即R(α,δ*)是一个只与p、q、n有关的常数，记为ρ*. 取参数α的先验分布列为

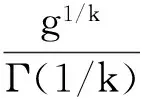
当k→∞时，有rπk(δ*)→ρ*. 于是，由引理2.1知，δ*(X)是参数α的最小最大估计.

3 结束语

Pareto分布参数的估计是现代统计文献中比较常见的研究内容，本文基于p,q对称损失函数，经由广义Bayes估计，在刻度参数给定条件下，较快捷地给出了形状参数的最小风险同变估计的精确形式，并证明了它还是该参数的最小最大估计.本文得到的估计形式更简捷，可根据需要灵活调整待定常数p,q的值以得到预期的估计形式.

[1] SAMUEL K, 吴喜之. 现代贝叶斯统计学[M]. 北京：中国统计出版社，2000.

[2] DIXIT D J, NOOGHABI M J. Efficient estimation in the Pareto distribution with the presence of outliers [J]. Stat Math, 2011,8(4):340-355.

[3] WU J W, LEE W C, CHEN S C. Computational comparison for weighted moments estimators and BLUE of the scale parameter of a Pareto distribution with known shape parameter under type II multiply censored sample [J]. Appl Math Comput, 2006,181(2):1462-1470.

[4] 康会光, 师义民. LINEX 损失下Pareto 分布族参数的经验Bayes估计[J]. 纯粹数学与应用数学，2001,17(2)：169-174.

[5] 谢天华, 叶 鹰. Pareto分布参数的渐进最优与可容许的经验Bayes估计[J]. 应用数学,2006,19(增)：237-240.

[6] 侯华蕾，师义民，李豪亮. 双边定数截尾下Pareto分布的可靠性[J].数理统计与管理，2009,28(5):826-830.

[7] 黄 娟. 右删失数据下Pareto分布参数经验Bayes渐进性质[J]. 工程数学学报, 2010,27(5)：781-788.

[8] 宋立新，王明秋，王晓光.q-对称熵损失函数下Pareto分布参数估计[J]. 大连理工大学学报， 2011,51(4):616-620.

[9] 王 芳，门 慧. 三参数广义帕累托分布的似然矩估计[J]. 数学年刊, 2013,34(3):299-312.

[10] 王 娟，徐付霞.Pareto 分布中尺度参数的区间估计[J]. 哈尔滨商业大学学报(自然科学版), 2015,31(5):629-633.

[11] YOGESH M T, SOMESH K, CONSTANTINOS P. Estimating the shape parameter of a Pareto distribution under restrictions[J]. Metrika, 2016,79(1):91-111.

[12] 徐 宝，姜玉秋，滕 飞. 一种加权对称损失函数下一类指数分布模型参数的估计[J]. 四川师范大学学报(自然科学版)，2011,34(4):484-487.

[13] 周光亚，赵振全，赵 文. 数理统计(Ⅱ)[M]. 长春:吉林大学出版社，1988.

[14] BERGER J O. Statistical decision theory and Bayesian analysis. 2nd ed[M]. New York:Springer，1985.

[15] 茆诗松，王静龙，濮晓龙. 高等数理统计[M].北京:高等教育出版社，1998.

MinimumRiskEquivariantEstimatorofParetoDistributionShapeParameter

XUBao*,WANGYu-ting,MAYi-guang

(Faculty of Mathematics, Jilin Normal University, Siping 136000, China)

For the Pareto distribution, in the present work, the form and property of the minimum risk equivariant estimator for shape parameters with known local parameters were investigated under weightedp,qsymmetric entropy loss by the method of parameter estimation. The general form of the minimum risk equivariant estimator was obtained, and the exact form of the minimum risk equivariant estimator was found using the general Bayes estimator of shape parameter. The minimaxity of this minimum risk equivariant estimator was proved. The relationships among the general Bayes estimator, the minimum risk equivariant estimator, and the minimax estimator have been established.

Pareto distribution; minimum risk equivariant estimator; Bayes estimator; minimax estimator

10.7612/j.issn.1000-2537.2017.06.013

2016-11-16

国家自然科学基金资助项目(11571138)

*通讯作者,E-mail：xubao97@163.com

O212.8

A

1000-2537(2017)06-0076-04

(编辑 HWJ)