Compact Spaclike Hypersurfaces of Lorent Space:New Integral Formulas and r-Mean Curvature

WANG Qi

(School of Mathematics and Information Science, Guiyang University, Guiyang 55005, China)

Compact Spaclike Hypersurfaces of Lorent Space:New Integral Formulas and r-Mean Curvature

WANG Qi

(School of Mathematics and Information Science, Guiyang University, Guiyang 55005, China)

LetMbe an oriented and compact spacelike hypersurface without boundary in the Lorentz spaceLn+1. In this work, we firstly attain a class of new integral formulas. Then we apply these integral formulas to prove thatMis totally umbilical if there exists an integerr(1≤r≤n-1) such that thei-mean curvatureHi>0,i=1,2,…,randHris constant.

Lorentz space; compact spacelike hypersurface; integral formula;r-mean curvature; totally umbilical property

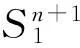
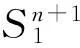
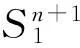
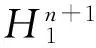
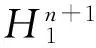
In this paper we study oriented and compact spacelike hypersurfaces without boundary in the Lorentz spaceLn+1. Firstly, we establish a class of new integral formulas, that is the following Theorem A.

TheoremALetMbe ann-dimensional, oriented and compact Riemann manifold without boundary. Letφ:M→Ln+1be a spacelike isometric immersion map. Then the following integral formulas hold.

HereNis the timelike unit normal vector field ofM,Hi(i=1,2,…,n) is thei-mean curvature ofManddVis the Riemann volume element ofM.

Then we apply the integral formulas of Theorem A to the case of constantr-mean curvature and we prove a new result, that is the following Theorem B.

We feel amazing for the symmetry among Theorem 1, Theorem 2 and our Theorem B.

TheoremBLetMbe ann-dimensional, oriented and compact spacelike hypersurface without boundary inLn+1. ThenMis totally umbilical if thei-mean curvatureHi>0,i=1,2,…,randHris constant for some integerr,r=1,2,…,n-1.

1 Preliminaries and proof of Theorem A

Denote byRn+1the (n+1)-dimensional Euclidean space and letRn+1be equipped with the following Lorentz metric[1-6],

〈，〉=-(dx0)2+(dx1)2+…+(dxn)2.

Here (x0,x1,…,xn) is the natural global coordinate forRn+1. Then we have the (n+1)-dimensional Lorentz spaceLn+1with negative index one.

Denote by (M,g) an-dimensional Riemann manifold and byφ:M→Ln+1an immersion map.

Ifg=φ*(〈,〉) holds, then we say thatMorφ(M) is a spacelike hypersurface isometricly immersed intoLn+1. Here 〈,〉 is the Lorentz metric ofLn+1.

Hereafter, we discuss integral formulas. Following the ideas in references [7,8], we study spacelike hypersurfaces isometricly immersed into the Lorentz spaceLn+1. We will give the following Lemma 1 indicating our Theorem A. For our purpose we firstly recall several basic concepts and conclusions.

LetMbe a Riemann manifold andSbe a tensor field of type (k,k) overM. When both the covariant components and the contra-variant components ofSare alternating, then we writeS∈Γ(EndΛk(TM)). ForS∈Γ(EndΛk(TM)),T∈Γ(EndΛj(TM)). We also considerS*T∈Γ(EndΛk+j(TM)), which have its covariant component as the exterior product of the covariant components inSandTrespectively, and its contra-variant component as the exterior product of contra-variant components inSandTrespectively.

We know that the operation * is associative and commutative ( see [7,8] ).

Definition1( Codazzi Tensor Field, [7,8] ) LetMbe a Riemann manifold and letS∈Γ(EndΛk(TM)). Then we say thatSis a Codazzi tensor field of type (k,k) overMif, for arbitrary smooth tangent vector fieldsX1,X2,…,Xk+1∈Γ(TM), the following formula

0=∑(-1)j+1(▽XjS)(X1∧X2∧…∧Xj-1∧Xj+1∧…∧Xk+1),

holds. Here ▽ is the Levi-Civita connection ofM.

When bothS∈Γ(EndΛk(TM)) andT∈Γ(EndΛj(TM)) are Codazzi tensor field overM, respectively of type (k,k) and of type (j,j), thenS*Tis also a Codazzi tensor field of type (k+j,k+j) overM( see [7,8] ). Denote by (M,g) ann-dimensional Riemann manifold and byφ:M→Ln+1a spacelike isometric immersion map. We need to define a symmetric tensor fieldAof type (1,1) overMby the following formula

g(A(X),Z)=g(A(Z),X)=〈II(X,Z),Y〉=〈II(X,Z),φ〉,X,Z∈Γ(TM).

Here 〈,〉 is Lorentz metric ofLn+1andYis the position vector ofφ(M) inLn+1.

Lemma1LetMbe ann-dimensional, orientable and compact Riemann manifold without boundary andφ:M→Ln+1be a spacelike isometric immersion. Assume thatSis a Codazzi tensor field of type (k,k) overM. Then the following integral formulas hold.

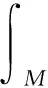
(1)

HeredVis the Riemman volume element ofMandAis a symmetric tensor field of type (1,1) as defined above in this section.

ProofDenote bydVthe volume element of M, then the following formulas

α(X1,X2,…,Xn-1)=(dV)(Ytan,X1,X2,…,Xn-1), ∀X1,X2,…,Xn-1∈Γ(TM).

can determinea(n-1) exterior differential form on M and we write it as

HereYtanis the tangent component of the position vectorYofφ(M) inLn+1.

Noticing that the timelike unit normal vector fieldNofMsatisfies 〈N,N〉≡-1, we have

(2)

Firstly, we consider the case thatSis a Codazzi tensor field of type (n-1,n-1) overM.

Lete1,e2,…,enbe any one of local unity orthogonal frame fields ofMand we write

Ej=e1∧…∧ej-1∧ej+1∧…∧en,j=1,2,…,n,E=e1∧e2∧…∧en.

We can considerω=α∘Sas aΓ(EndΛn-1(TM))-valued (n-1) form, and we have

dω(e1,e2,…,en)=∑(-1)j+1(▽ejω)(Ej)=

∑(-1)j+1(▽ejα)°S(Ej)+α°∑(-1)j+1(▽ejS)(Ej).

SinceSis a Codazzi tensor field, the second term of the above formula is zero. Thus from equation (2) we have

∑(-1)j+1〈ej∧S(Ej),E〉-∑(-1)j+1〈A(ej)∧S(Ej,E)〉=

∑〈ej∧S(Ej),ej∧Ej〉-∑〈A(ej)∧S(Ej),ej∧Ej〉=trace(S)-trace(S*A).

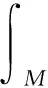
Now we assume thatSis a Codazzi tensor field of type (k,k). And Let be the identity element ofΓ(EndΛn-k-1(TM)).

SinceIis parallel,S*Iis a Codazzi tensor field of type (n-1,n-1) overMand we have

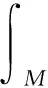
Finally, we have ( see [7,8] )

trace(S*I)=(n-k)trace(S), trace(S*A*I)=trace(S*A),

and we already finish the proof of Lemma 1.

Now we are in the position to prove our Theorem A.

TheoremALetMbe ann-dimensional, oriented and compact Riemann manifold without boundary. Letφ:M→Ln+1be a spacelike isometric immersion map. Then the following integral formulas hold.

HereNis the timelike unit normal vector field ofM,Hi(i=1,2,…,n) is thei-mean curvature ofManddVis the Riemann volume element ofM.

ProofFirstly, sinceMis an orientable and compact spacelike hypersurface,Mhas a global timelike unit normal vector fieldN.

LetTbe the shape operator ofM,that isTa tensor field of type (1,1) overMdefined by

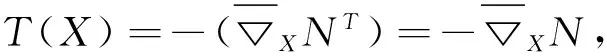
Denote byλ1,λ2,…,λnthe characteristic values ofTand byσkthek-th element symmetric poly-nomial ofλ1,λ2,…,λn. LetS=Tk=T***T(*productk-times ). Following the computation of references [7,8], we have

trace(S)=k!σk.

(3)

Denote byh=h(x)=〈φ(x),N(x)〉,x∈M, the support function ofM. Then it is easy to know

A=-hT.

By direct computation similar to that for equation (3) we have

trace(S*A)=-h(k+1)!σk+1.

(4)

2 Proof of Theorem B

For expression convenience of our proof for Theorem B, here we state Theorem B in the following equivalent form.

TheoremBLetMbe ann-dimensional, oriented and compact Riemann manifold without boundary. Letψ:M→Ln+1be a spacelike isometric immersion map. ThenMis totally umbilical if thei-mean curvatureHi>0,i=1,2,…,randHris constant for some integerr,r=1,2,…,n-1.

ProofWe need the following well-known algebraic inequalities[1,2,4,10]

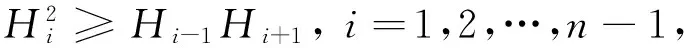
(5)

And any one of the equality signs in (5) holds if and only if at an umbilical point ofM.

Take an arbitrarily fixed vectora∈Ln+1and we consider the mapφ:M→Ln+1defined as

φ(x)=ψ(x)+a,x∈M.

(6)

Since the tangent mapdφ=dψ, we know thatφ(M) andψ(M) have the same tangent space at a pair of corespondent points. And soφ(M) is also a compact spacelike hypersurface ofLn+1.

Still denote byNthe timelike unit normal vector field ofφ(M). Using the integral formulas of Theorem A forφ(M), we have

(7)

(8)

SinceHris a nonzero constant, from (7) we have

(9)

Combining (8) and (9), we have

(10)

Noticing (5) and our assumption thatH1>0,H2>0,…,Hr>0, we have

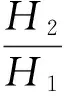
(11)

and so we have

H1Hr-Hr+1≥0, ∀x∈M.

(12)

We can select a suitable fixed vectora∈Ln+1in (6) such thatφ(M) completely lies in the interior of the light cone ofa∈Ln+1.

Since the Lorentz inner product of any two timelike vectors can not be zero and we generally assume thatMis connected, the Lorentz inner product 〈φ,N〉 does not change its sign overM. Then, without loss of generality, we can assume

〈φ,N〉=〈φ(x),N(x)〉>0, ∀x∈M.

(13)

Now, combining (9), (12) and (13) we have

H1Hr-Hr+1=0, ∀x∈M.

(14)

Finally, by combining (11) and (14) we know that each one of inequality signs in (11) actually reaches equality sign at each point ofM.

Thus from the condition of any one of the inequality signs in (5) reaching equality sign, we conclude thatφ(M) is totally umbilical.

On the other hand, it is obvious that the totally umbilical property is invariant under any one translation inLn+1.

And so we already prove thatψ(M) is totally umbilical.

[1] LI H Z, CHEN W H. Integral formulas for compact spacelike hypersurfaces in de Sitter space and their applications to Goddard’s conjecture [J]. Acta Math Sin, 1998, 14 (2), 285-288.

[2] 徐森林,胡自胜.Anti de Sitter 空间中紧致类空超曲面的积分公式及其在稿件平均曲率下的应用[J].数学物理学报， 2007，27A (2)：302-308.

[3] 聂昌雄，吴传喜.共形空间中平行的第二基本形式的类空超曲面[J].数学学报，2008，51(4)：685-692.

[4] 聂昌雄，于艳梅，郑立荷.具有平行的第二基本形式的类时超曲面[J].数学学报，2015，58(6)：897-910.

[5] 张远征. Lorentz 空间中常平均曲率类空超曲面[J]. 数学学报，2002,45(3)：571-574.

[6] 张远征.有界 F-支撑函数和类空 Wulff 形[J]. 数学学报，2016，59(1)：37-46.

[7] BIVENS I. Codazzi tensors and reducible submanifolds [J].Trans Am Math Soc, 1981, 268 (1): 231-246.

[8] BIVENS I. Integral formulas and hypersurfaces in a simply connected space form [J]. Proc Am Math Soc, 1983,88(1):113-118.

[9] 王 琪. Anti de Sitter 空间中全脐类空超曲面与高阶平均曲率[J].山西大学学报(自然科学版)，2016,39(3)：403-405.

[10] ALENCAR H, ROSENBERG H, SANTOS W. On the Gauss map of hypersurfaces with constant scalar curvature in spheres [J]. Proc Am Math Soc, 2004,132(12):3731-3739.

2016-10-28

贵州省科学技术基金资助项目(黔科合LH字[2015]7298)*通讯作者,E-mail：wangqihn@126.com

O186.16

A

1000-2537(2017)06-0066-05

洛伦兹空间中紧致类空超曲面：新积分公式与高阶平均曲率

王 琪*

(贵阳学院数学与信息科学学院，中国 贵阳 550005)

设M是洛伦兹空间Ln+1中紧致无边定向类空等距浸入超曲面.首先得到一类新的积分公式.然后，通过应用这些积分公式，证明了：如果存在一个整数r(1≤r≤n-1)使得高阶平均曲率Hi>0,i=1,2,…,r，而且Hr是常数， 则M是全脐的.

洛伦兹空间；紧致类空超曲面；积分公式；高阶平均曲率；全脐性质

10.7612/j.issn.1000-2537.2017.06.011

(编辑 HWJ)