利用敏感频段评估大规模风电对电力系统频率影响的方法

安 军, 冯 琦, 穆 钢, 李泽宇, 岳 涵, 王克非

(1. 东北电力大学电气工程学院, 吉林省吉林市 132012; 2. 国网山东省电力公司烟台供电公司, 山东省烟台市 264000; 3. 国家电网东北电力调控分中心, 辽宁省沈阳市 110000)

利用敏感频段评估大规模风电对电力系统频率影响的方法

安 军1, 冯 琦2, 穆 钢1, 李泽宇3, 岳 涵3, 王克非3

(1. 东北电力大学电气工程学院, 吉林省吉林市 132012; 2. 国网山东省电力公司烟台供电公司, 山东省烟台市 264000; 3. 国家电网东北电力调控分中心, 辽宁省沈阳市 110000)

随着系统中风电渗透率的增加,风功率波动对电力系统频率的影响不可忽视。首先定义了“敏感频段”的概念,对单机系统频率响应模型进行分析,揭示了不同频率的功率扰动对系统频率特性影响程度的差异。其次,计及复杂电力系统的非线性特性,提出了利用聚类思想识别其敏感频段的分区域扫频法。最后,给出了从敏感频段角度分析风功率波动对电力系统频率特性影响的分析方法,结合风功率波动的幅频特性评估其对电网频率的影响,通过东北电网算例证实了敏感频段的存在,验证了所提方法的有效性。

敏感频段; 风功率波动; 复杂电力系统; 频率特性

0 引言

近年来,风力发电在电力系统中所占比重逐渐增加。截至2016年,中国风电总装机容量已达到169 GW,预计到2020年,中国风电累计装机容量将达到2×108kW[1-2]。大规模风电的随机性、波动性给电力系统的稳定运行尤其是频率稳定带来了新的挑战[3-4]。研究高渗透率风功率波动对电力系统频率的影响,可为含高比例风电电力系统的安全运行提供重要的指导[5-7]。

目前风功率波动对电力系统频率影响的研究主要有如下的分析方法。

1)风电功率波动建模分析法[8-11]。即通过建立不同的风功率波动的概率分布函数来描述风功率波动的特性,进而分析其对系统频率的影响。该方法虽然能够较为完整地描述风功率的波动特性,但其概率模型的建立缺少实测功率波动数据的支持,针对不同的风速条件,其风功率模型缺乏普适性。

2)基于实测的风功率波动特性分析法[12-17]。该方法通过风功率的秒级或毫秒级实测数据,分析其相应的波动特性指标,如最大波动量、波动速度等,从而对电力系统的频率稳定性进行评估。文献[12]依据风功率波动的时域曲线,定义了最大功率波动量及最大功率波动率等衡量风功率波动特性的指标。并在实际电网算例中依据提出的指标评估不同水平的风功率波动对系统频率的影响。文献[13]对风功率波动的频域特性进行分析,发现对系统频率影响最为显著的是中频的风功率波动(0.1～10 Hz)。该研究结合系统的频率响应特性,具有较强的普适性,为以后的风功率波动的平抑工作提供了一定的理论基础,但是没有量化分析不同频率的功率波动对系统频率的影响程度。文献[14]通过构造系统频率响应模型,结合风功率波动的实测数据,提出了一种风电功率波动对电力系统频率响应的快速评估方法,该研究并未计及复杂电力系统的非线性特性,在实际电网中的应用需要进行进一步的研究。

本文拟从研究对电力系统频率响应最为剧烈的功率波动频段入手,分析风功率波动对于系统频率的影响,在文中提出了一种适用于复杂非线性电力系统敏感频段的识别方法,并建立了一套从电网敏感频段角度评估风功率波动对电力系统频率特性影响的流程,最后对于大电网的算例分析验证了所提方法的有效性。

1 电力系统敏感频段特性

对于一个物理系统,由于其内部的结构关系,存在着一个固有频率。当系统受到外界的扰动时,该系统会通过振动消耗能量。若外界扰动的振动频率与系统的固有频率相同时,外界扰动会与系统产生共振,系统的振幅会达到最大,该频率也叫系统的共振频率。

对于电力系统,由于其包含发电机、调速器等机械元件,故电力系统也存在着一定的固有频率,其固有频率与系统中发电机、调速器等元件的参数有关。当电力系统受到功率扰动时,将导致系统的频率发生变化,若外界的功率波动扰动频率与电力系统固有频率相等或接近系统的固有频率时,电力系统的频率响应最为剧烈,而处于电力系统固有频率附近频段的功率波动对系统频率特性也会有较大的影响,该频段即称为电力系统的敏感频段。

目前在对电力系统频率响应问题进行分析时,通常采用Andersen提出的有功功率—频率的系统频率响应模型,其单机系统频率响应模型如图1所示[18]。

图1 单机系统频率响应框图Fig.1 Diagram of frequency response for single machine system

图1中:2H和D分别为发电机的惯性时间常数和阻尼系数;T1和T0分别为调速器伺服时间常数和蒸汽容积时间常数;Km为放大倍数;R为发电机调差系数。在上述框图中,系统频率偏差Δf与系统有功功率扰动量ΔP之间的传递函数G(s)可表示为:

(1)

依据文献[18]对上述传递函数G(s)中的相关参数的设置如附录A表A1所示,式(1)传递函数的幅频特性如图2所示。

图2 传递函数G(s)幅频特性Fig.2 Amplitude frequency characteristic of transfer function G(s)

由图2中可以看出,以系统频差不超过0.1 Hz为限,当功率波动的频率在2～3 Hz之间时,系统频差会超过限值,说明该系统对2～3 Hz的功率波动的频率响应最为敏感,即系统存在敏感频段。

2 复杂电力系统敏感频段识别

在多机电力系统中,也会存在一定区间的敏感频段,处于该频段内的功率波动对于系统频率响应最为敏感。由于电力系统是一个非线性系统,相同的功率扰动在不同运行方式下、不同地点处产生的频率响应并不完全相同,因此,图1的单机系统模型分析方法难以应用于复杂非线性电力系统中。

本文将聚类思想引入复杂电力系统频率响应的分析中,采用分区域扫频法对电力系统的敏感频段进行识别。

电网在正常运行时,其运行状态通常处于额定运行状态附近,其运行状态变化较小,因此,本文假设系统的运行状态对非线性的影响可以忽略。

本文对复杂电力系统敏感频段的识别流程主要分为以下3个部分:①获取频率响应样本;②对频率响应样本进行聚类分析;③分区域识别系统敏感频段。其各部分的具体流程如下。

2.1 频率响应样本获取

频率响应样本的获取即是选取电力系统中若干节点作为样本,获取每个样本在受到不同功率波动幅值及波动频率的功率扰动时系统频率动态特性,以体现出电力系统的非线性特性,为下一步的聚类分析提供样本,本文对于系统频率响应样本的获取,采用了变幅值频率扫描法。

变幅值频率扫描法即是对所选取的样本节点施加ΔP=Asin(2πfwt)的正弦功率波动,通过设定不同的功率波动幅值A与波动频率fw,可以得到不同功率波动幅值及波动频率下的系统频率响应,取系统在上述功率扰动下频率响应的最大频差|Δfmax|,即可得到每个样本节点频率响应的最大频差矩阵如式(2)所示。

(2)

式中:C的行数代表正弦功率扰动中波动频率变化的次数,列数代表正弦功率扰动中波动幅值变化的次数,该矩阵反映了某节点在受到不同幅值及频率的功率扰动时的频率响应程度。

2.2 频率响应样本聚类分析

由于电力系统的非线性特性,不同节点通过频率扫描法得到的C矩阵中元素均存在差异,本文采用聚类的思想,通过所选取的节点对复杂电力系统的敏感频段进行识别。

聚类分析又称群分析,它是研究(样品或指标)分类问题的一种统计分析方法,同时也是数据挖掘的一个重要算法。通过计算每个样本之间的距离,将样本分成指定的区域数[19-20]。在本文中,对于不同节点处的频率响应样本,采用K-means聚类算法,该聚类算法具有简单快速的优点,对于数据量较大的样本集的分类效率高,适用于复杂电力系统多地点频率响应特性的聚类分析。

对于复杂电力系统,在N个节点上均施加不同幅值及频率的正弦功率波动,得到N个最大频差矩阵C,为简化聚类算法的计算过程,可将矩阵C转换成列向量后,计算任意两个列向量xi与xj间的欧式距离,其计算如式(3)所示。

(3)

K-means聚类算法首先在样本中任选k个点作为聚类的初始中心,并计算其余样本到中心点的欧氏距离,选取距离最小的中心点归为一类,并通过使得所有样本到各自中心点最近的目标函数来不断迭代选取中心点,从而完成对样本的聚类。

对于聚类后电力系统每一个区域内的节点,可认为该区域中电网在相同的功率扰动下频率响应特性相同,通过判断频率响应的最大频差是否超过所设定的阈值,即可识别复杂电力系统各区域不同功率波动幅值所对应的敏感频段范围。对于电网中任意节点的敏感频段,可参照与其电气距离最小的样本节点所在的区域。依据电网的敏感频段,即可评估风功率波动对于电力系统频率的影响程度。

3 风功率波动对电网频率特性影响评估

在对复杂电力系统敏感频段的范围进行识别后,可基于电力系统敏感频段范围,结合实测风功率波动数据,评估该时段的风功率波动对于电网频率的影响程度,其具体评估流程如图3所示。

选取电网中不同节点,采用变幅值扫频获取各节点C矩阵样本,并对样本进行聚类分析,以设定的最大频差阈值为限,获取区域样本在不同功率波动幅值Ai下敏感频段的范围。该敏感频段范围反映了电网抗敏感功率波动的能力。

图3 风功率波动对电网频率影响评估流程Fig.3 Influence assessment process of wind power fluctuation on power grid frequency

对容量为SN的风电场功率波动的时域数据进行傅里叶变换,转化为复频域数据,结合该风电场所在区域电网敏感频段范围,统计处于电网敏感范围内的风功率波动的最大幅值Pm。

比较Pm与电网可承受的敏感功率波动幅值Ai的大小,若Pm>Ai,则说明该处风电场风功率波动中的敏感风功率波动会造成电网频率发生越限;反之,则可说明该风电功率波动不会造成电网频率越限,而对于此处风电的最大接纳量(Smax)可通过式(4)计算得到:

(4)

式(4)即为评估复杂电力系统中风电接纳水平的计算公式,该评估方法从系统侧给出了计及电力系统非线性特性和风功率波动实际情况,以最大频差为约束的电力系统风电接纳能力。

4 仿真算例分析

本文以2013年东北地区电网为例,计算当前运行方式下东北电网敏感频段,定量分析不同频段、不同幅值的功率波动对电网频率的影响程度。并结合东北电网内某风电场风功率波动广域测量系统(WAMS)数据,评估目前东北电网内的风功率波动对于电网频率的影响程度,并对未来东北电网所能接纳的风电水平进行预测。

4.1 算例介绍

东北电网包括黑龙江、吉林、辽宁及内蒙古东部4个地区电网,在本算例运行方式中,各地区内发电机负荷规模如附录A表A2所示。

其中算例中同步发电机组均采用二阶模型,并配有调速器参与系统调频。由附录A表A2中的统计结果可知,目前运行方式下,系统发电量占系统总装机容量的64.2%。且该运行方式下,系统风电功率的渗透率为7.25%。

4.2 电网敏感频段识别

对于上述东北电网算例,使用变幅值扫频法识别电网敏感频段范围时,首先需确定敏感频段的大致区间,在该区间内设置扫频法频率变化步长进行扫描。本文中,通过对“辽宁.庄河厂500 kV”节点进行阶跃扰动频率响应计算,可知该电网敏感频段在0.01～0.06 Hz的区间内(相关计算结果见附录B),因此可在该区间内进行电网的敏感频段识别。

依据图3电网风电接纳容量的计算流程,选取电网中不同地点的节点进行变幅值扫频分析,获得频率响应的最大频差矩阵样本,对样本进行聚类分析后得出不同区域敏感频段的范围。本次分析选取东北电网内40个样本节点(吉林、辽宁、黑龙江、蒙东地区各10个节点,所选取的具体节点见附录C),对40个节点分别施加ΔP=Asin(2πfwt)的正弦功率扰动,在本次仿真中,功率波动幅值A从200 MW变化至400 MW,其幅值变化步长为10 MW;功率波动频率从0.01 Hz变化至0.06 Hz,其频率变化步长为0.001 Hz。

以“辽宁.丹东220 kV”母线为例,在该母线施加变幅值扫频法时,得到的系统最大频差响应的三维图如图4所示。

图4 辽宁.丹东220 kV母线不同幅值及频率功率扰动下频率响应最大频差Fig.4 Maximum frequency difference of frequency response under different amplitudes and frequency power disturbances in Liaoning. Dandong 220 kV bus

从图4中最大频差的分布可以看出,功率扰动的幅值越大,对系统频率的影响程度越高,但在相同的功率波动幅值下,都存在着系统频率响应更为剧烈的功率波动频段,该频段内的功率波动更容易造成系统频率的越限。

对于上文选取的40个样本节点,均进行相同的变幅值扫频分析,可得到40个最大频差矩阵,采用的聚类算法为K-means聚类算法,设置聚类区域数k=4,得到样本聚类的谱系见附录C图C1(各母线编号见附录C),聚类后各区域所包含的母线数目级母线编号见附录C表C2。

对于附录C表C2聚类后处于同一区域的节点,可认为在相同的有功功率扰动下,其频率特性近似相同,对于不在选取样本范围内的节点,其发生功率扰动时的频率动态特性可参照离该节点电气距离最近的样本。

为评估各区域节点的敏感频段范围,以电网二次调频的动作频率偏差0.1 Hz为最大频差阈值,若电网的频率偏差大于0.1 Hz,则认为此时的功率波动频率即处于该节点敏感频段范围内。对于上述4个区域,在不同功率波动幅值下的敏感频段范围如表1所示。

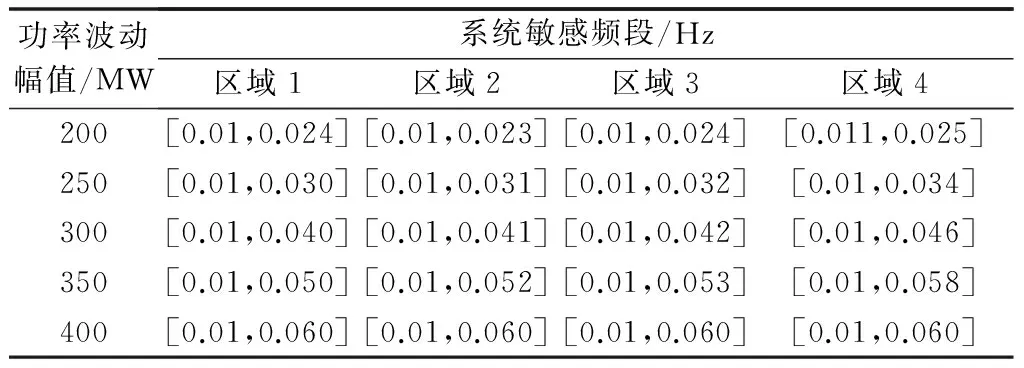
表1 不同功率波动幅值下系统敏感频段范围统计Table 1 Statistical ranges of system sensitive frequency bands under different power fluctuation amplitudes

依据表1中不同功率波动幅值下各区域敏感频段的统计,即可评估功率波动对系统频率响应的影响程度,运行人员可依据上述评估结果识别电网不同节点的敏感频段范围,并对处于系统敏感频段范围内的功率波动分量进行抑制,维护电力系统的频率稳定。

4.3 风功率波动对电网频率影响评估

在识别电网不同地点敏感频段范围后,可通过分析该节点现有的风电场装机容量及功率波动频率特征,从敏感频段角度评估风功率波动对电网频率影响程度。

本文对于东北电网实测风功率波动数据的分析采用辽宁省康平县某风电场,该风电场装机容量为99 MW(1.5 MW×66台)。采用其配置的相量测量单元(PMU)数据,其中数据采样时间间隔为0.02 s,采样时间256 s,该风电场输出功率变化如图5所示。

图5 风电场有功功率波动曲线Fig.5 Active power fluctuation curve of wind farm

对上述风功率波动进行快速傅里叶变换,其部分结果如表2所示。

表2 风功率波动傅里叶变换结果Table 2 Fourier transform results of wind power fluctuations

从上述对东北电网各区域敏感频段的计算可知,该风电场属于第3号区域,风功率波动频率为0.009 2 Hz的功率波动分量为12.23 MW,结合表1的统计可知,该频率的功率波动下,使得系统频率偏差超过0.1 Hz所需的功率波动幅值为200 MW。该波动幅值远低于使系统二次调频动作的敏感功率波动幅值,因此,在目前的风电装机容量下,正常的风功率波动不会造成系统频率越限。

若该地区风电装机容量持续增加,假设风功率波动的幅值与该地区风电装机容量呈等比例变化,可根据式(4)计算得到为使系统频率不发生越限,该地点所能接纳的最大风电装机容量为{Smax}MW=99×200/12.23=1 619。

当该风电场装机容量达到1 619 MW时,该时刻的敏感风功率波动会触发系统的二次调频。此外,若系统中风电渗透率增加,火电机组退出运行,系统的整体惯性降低,其抗敏感风功率波动的能力也会减弱。因此,实际能够对系统频率稳定性产生影响的风电场最大装机容量将小于上述数值。

5 结语

本文提出了一种从系统敏感频段角度评估风功率波动对于系统频率特性影响程度的评估方法。该方法解决了复杂电力系统敏感频段的定位问题,同时揭示了功率波动对复杂电力系统频率的影响机理。对东北电网的算例分析验证了该方法的有效性,为评估电力系统风电接纳水平提供了一种新的方法,对保证未来高风电渗透率电力系统的频率具有指导意义。

本文的研究并未考虑电网仿真模型与实际系统的吻合程度,下一步的研究将集中在计及仿真模型可信度的敏感频率识别,并进一步研究分布式可再生能源并网对电网频率响应的影响。

附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。

[1] 中国风能协会.2016年中国风电装机容量简报[EB/OL].[2017-02-17].http://news.bjx.com.cn/html/20170217/808890.shtml.

[2] 世界风能协会.2016年度世界风能发展[EB/OL].[2017-02-15].http://www.360doc.com/content/17/0215/21/9950369_629288683.shtml.

[3] 袁小明,程时杰,文劲宇.储能技术在解决大规模风电并网问题中的应用前景分析[J].电力系统自动化,2013,37(1):14-18.

YUAN Xiaoming, CHENG Shijie, WEN Jinyu. Prospects analysis of energy storage application in grid integration of large-scale wind power[J]. Automation of Electric Power Systems, 2013, 37(1): 14-18.

[4] 丁立,乔颖,鲁宗相,等.高比例风电对电力系统调频指标影响的定量分析[J].电力系统自动化,2014,38(14):1-18.DOI:10.7500/AEPS20130810001.

DING Li, QIAO Ying, LU Zongxiang, et al. Impact on frequency regulation of power system from wind power with high penetration[J]. Automation of Electric Power Systems, 2014, 38(14): 1-18. DOI: 10.7500/AEPS20130810001.

[5] ZHANG Wei, FANG Kailun. Controlling active power of wind farms to participate in load frequency control of power systems[J]. IET Generation, Transmission & Distribution, 2017, 11(9): 2194-2203.

[6] AKBARI M, MADANI S M. Analytical evaluation of control strategies for participation of doubly fed induction generator-based wind farms in power system short-term frequency regulation[J]. IET Renewable Power Generation, 2013, 8(3): 324-333.

[7] RENUKA T K, REJI P. Participation of doubly FED induction generator based wind turbines in power system primary frequency regulation[C]// International Conference on Emerging Trends in Engineering & Technology, 2015, Ajmer, India: 310-315.

[8] 林文星,文劲宇,艾小猛,等.风电功率波动特性的概率分布研究[J].中国电机工程学报,2012,32(1):38-46.

LIN Wenxing, WEN Jinyu, AI Xiaomeng, et al. Probability density function of wind power variations[J]. Proceedings of the CSEE, 2012, 32(1): 38-46.

[9] 崔杨,刘嘉,严干贵,等.联网风电功率波动对电力系统频率影响评估[J].太阳能学报,2014,35(4):617-623.

CUI Yang, LIU Jia, YAN Gangui, et al. Effect of on-grid wind power fluctuation on frequency stability of electric power system[J]. Acta Energiae Solaris Sinica, 2014, 35(4): 617-623.

[10] WANG X L, CHOI S S. A statistical approach to assess the impact of wind power generation on network frequency[C]// IEEE International Conference on Control and Automation, 2009, Christchurch, New Zealand: 1692-1696.

[11] CUI Yang, MU Gang, LIU Yu, et al. Spatiotemporal distribution characteristic of wind power fluctuation[J]. Power System Technology, 2011, 35(2): 110-114.

[12] 蒋大伟.大规模风电并网对系统频率影响分析[D].吉林:东北电力大学,2010.

[13] BANAKAR H, LUO C L, OOI B T. Impacts of wind power minute-to-minute variations on power system operation[J]. IEEE Trans on Power Systems, 2008, 23(1): 150-160.

[14] 徐箭,施微,徐琪.含风电的电力系统动态频率响应快速评估方法[J].电力系统自动化,2015,39(10):22-27.DOI:10.7500/AEPS20141012003.

XU Jian, SHI Wei, XU Qi, et al. A fast assessment method for power system dynamic frequency response to wind power fluctuation[J]. Automation of Electric Power Systems, 2015, 39(10): 22-27. DOI: 10.7500/AEPS20141012003.

[15] 黄亚峰,穆钢,刘嘉,等.基于带阻滤波原理的风电场功率波动平抑策略研究[J].太阳能学报,2012,33(7):1073-1079.

HUANG Yafeng, MU Gang, LIU Jia, et al. Study on the strategy for smoothing power fluctuations of wind farms based on the principle of band-stop filter[J]. Acta Energiae Solaris Sinica, 2012, 33(7): 1073-1079.

[16] LIN Jin, SUN Yuanzhang, SØRENSER P, et al. Method for assessing grid frequency deviation due to wind power fluctuation based on “time-frequency transformation”[J]. IEEE Trans on Sustainable Energy, 2012, 3(1): 65-73.

[17] LUO Changling, FAR H G, BANAKAR H, et al. Estimation of wind penetration as limited by frequency deviation[J]. IEEE Trans on Energy Conversion, 2007, 22(3): 783-791.

[18] ANDERSON P M, MIRHEYDAR M. A low-order system frequency response model[J]. IEEE Trans on Power Systems, 1990, 5(3): 720-729.

[19] 赵永宁,叶林,朱倩雯.风电场弃风异常数据簇的特征及处理方法[J].电力系统自动化,2014,38(21):39-46.DOI:10.7500/AEPS20131213010.

ZHAO Yongning, YE Lin, ZHU Qianwen. Characteristics and processing method of abnormal data cluster caused by wind curtailments in wind farms[J]. Automation of Electric Power Systems, 2014, 38(21): 39-46. DOI: 10.7500/AEPS20131213010.

[20] 张东英,李伟花,刘燕华,等.风电场有功功率异常运行数据重构方法[J].电力系统自动化,2014,38(5):14-18.DOI:10.7500/AEPS20130518005.

ZHANG Dongying, LI Weihua, LIU Yanhua, et al. Reconstruction method of active power historical operating data for wind farm[J]. Automation of Electric Power Systems, 2014, 38(5): 14-18. DOI: 10.7500/AEPS20130518005.

MethodforEvaluationEffectsofLarge-scaleWindPoweronFrequencyofPowerSystembyUsingSensitiveFrequencyBand

ANJun1,FENGQi2,MUGang1,LIZeyu3,YUEHan3,WANGKefei3

(1. School of Electrical Engineering, Northeast Electric Power University, Jilin 132012, China; 2. Yantai Electric Power Company of State Grid Shandong Electric Power Company, Yantai 264000, China; 3. State Grid Northeast China Electric Power Dispatching & Controlling Center, Shenyang 110000, China)

With an increase of wind power penetration rate, the influence of system frequency stability due to wind power cannot be ignored. Firstly, the concept of “sensitive frequency band” is defined. In order to find the frequency characteristic difference between power disturbances with different frequencies, the frequency response model of single machine system is analyzed. Secondly, considering the nonlinear characteristics of complex power systems, the method of cluster scanning is proposed to recognize the sensitive frequency bands of complex power systems. Finally, the method of analysis of the influence of wind power fluctuation on the frequency characteristics of power system by analyzing the sensitive frequency band is given. The existence of a sensitive frequency band is verified by an example of the Northeast power grid. Its influence on the grid power is evaluated by referring to the amplitude frequency characteristics of the wind power fluctuation and the effectiveness of the proposed method.

This work is supported by National Key Research and Development Program of China (No. 2016YFB0900100) and Education Commission of Jilin Province ([2016] No. 91).

sensitive frequency band; wind power fluctuation; bulk power system; frequency characteristic

2017-06-11;

2017-08-07。

上网日期: 2017-09-12。

国家重点研发计划资助项目(2016YFB0900100);吉林省教育厅项目(吉教科合字[2016]第91号)。

安 军(1978—),男,博士,教授,主要研究方向:电力系统动态分析与控制。E-mail： 173681572@qq.com

冯 琦(1992—),男,通信作者,硕士研究生,主要研究方向:电力系统动态安全分析。E-mail: 790357443@qq.com

穆 钢(1957—),男,教授,主要研究方向:电力系统稳定与风力发电。

(编辑孔丽蓓)