针对电网阻抗的大型光伏并网系统稳定性分析与提高策略
张前进, 周 林, 解 宝
(输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆市 400044)
针对电网阻抗的大型光伏并网系统稳定性分析与提高策略
张前进, 周 林, 解 宝
(输配电装备及系统安全与新技术国家重点实验室(重庆大学), 重庆市 400044)
大型光伏并网系统中,一般采用多逆变器并联结构来提高总的光伏并网系统的容量。由于光伏电站的结构特点,随着并网容量的增加,电网阻抗值相对于某一个光伏发电单元而言将会被等效放大,从而导致逆变器控制策略失效且并网失败。文中在光伏并网系统开关平均模型的基础上,详细分析了电网阻抗对于逆变器输出电压和电流的影响,并针对电网阻抗导致的光伏并网系统的不稳定现象,采用虚拟阻抗思想,通过输出电流反馈,实现指令电流与输出电流的协调配合,等效消除电网阻抗对并网电压稳定性和并网电能质量的影响,从而保证系统的稳定运行。最后,通过仿真分析和试验验证了理论分析的正确性。
大型光伏并网系统; 电网阻抗; 稳定性; 电能质量; 虚拟阻抗
0 引言
由于传统能源具有不可再生和污染环境等缺点,随着经济的发展,能源危机、环境恶化等问题使得世界各国都在积极发展可再生清洁能源,并规划以清洁可再生的新能源逐步替代传统能源。在新能源体系中,风力发电和太阳能发电所占的比例最大,并且有资料显示美国、欧洲等西方发达国家在未来发展中都会逐步加大光伏发电所占的比例[1]。
目前,若干兆瓦级并网光伏电站相继在青海、甘肃、宁夏等地运行投产,宁夏盐城2 GW光伏电站也在建设当中。可以看出,大型光伏电站一般建在西部偏远地区。西部地区由于经济发展落后,大量的光伏电能并不能由本地负载消纳,因此需要将过剩的电能输送到东部发达地区,否则大容量光伏电站就只能降额运行。然而,国家对电网建设的投资和审批严重滞后于电源建设进度,因此西北地区仍存在很严重的“弃光”现象。滞后的输电线路对光伏输出容量的限制体现在其等效电网阻抗上,长距离输电线路产生的电网阻抗对光伏并网系统具有很大的影响,会引起并网系统谐波谐振、电压稳定性等问题。
文献[2]基于LCL滤波器的电流控制系统,分析了电网阻抗对于电流控制带宽的影响,采用谐波补偿和有源阻尼来抑制大范围电网阻抗变化导致的系统不稳定问题,但是研究对象为分布式并网系统,不能准确反映大型光伏电站的阻抗特性。文献[3]描述了由于电网阻抗作用而耦合的多逆变器并联光伏并网系统存在的控制稳定性问题,在考虑数控延时等因素下,提出了逆变器有源阻尼和控制算法的设计思路。文献[4]建立了大型光伏电站的诺顿等效模型,分析了考虑电网阻抗时大型光伏电站的谐振机理,并用根轨迹法判断大型光伏电站的稳定运行域。文献[5]针对多逆变器并联系统,推导出系统的全局最小环路增益并以此来判断系统的稳定性,从而避免多逆变器系统计算带来的复杂性。以上文献针对电网阻抗对于系统稳定性的影响,主要侧重于光伏电站等效阻抗与电网阻抗相匹配时的谐振现象,以及电网阻抗变化对于逆变器电流内环闭环控制系统稳定性的影响,并没有考虑大电网阻抗条件下,电网阻抗对于逆变器交流侧电压的影响。文献[6]简要分析了电网阻抗对于并网电压的影响,但并没有进一步分析其导致的系统稳定性问题及相应的抑制策略。然而,对于多逆变器并联系统,文献[7]提出当各逆变器结构、参数及控制方式等都相同时,多逆变器并联系统可以等效为单逆变器并网的观点,即对于大型光伏并网系统而言,特别是在光伏电站容量不断扩大的情况下,较大的电网阻抗不仅会对电流环控制系统的稳定性产生影响还会由于降低逆变侧电压而导致系统不稳定现象的发生。
本文首先对大型光伏并网系统的结构及控制策略进行简要介绍。然后讨论分析了电网阻抗对于逆变器输出电压、并网电能质量和系统稳定性的影响,在大型光伏电站扩容或输出容量较大的情况下,针对电网阻抗导致的并网电压崩溃从而造成的脱网事故,本文所提反馈策略,通过逆变器自身的控制,实现逆变器输出容量的自适应调节,保证并网电压的稳定,通过牺牲部分功率,保证整个光伏电站的稳定运行。弥补了实际中由于输电线路建设落后而导致的大容量系统并网失败的缺点,相比于无功补偿电网阻抗方式,该方法不增加额外的附加装置,减少了设备投资,适用于脱网事故的紧急情况,具有较大的应用价值。
1 大型光伏并网系统分析
由于大型光伏电站都是由一个个光伏发电单元组成的,大型光伏电站的稳定运行,离不开每个光伏发电单元的稳定。因此,本文先对单个500 kW光伏发电单元系统进行简要介绍。由于大型光伏电站具有容量大、控制系统复杂等特点,为提高效率,降低电能变换过程中能量的损失,其主电路结构采用单级结构[8]。对于开关频率较低的大容量逆变器,LCL滤波器相比于单L滤波器具有三阶低通滤波特性,在相同的谐波标准下可以采用较小的滤波电感设计,可以有效减小体积和成本[9],系统主电路等效框图见附录A图A1。
由于LCL滤波器的三阶滤波特性,其传递函数存在缺项,其特征方程将会出现在虚轴和原点处的极点,即LCL滤波器存在谐振现象。为抑制LCL滤波器的谐振峰值,本文采用电容电流反馈的有源阻尼策略[10-12]。此外,对于LCL并网型逆变器,在dq旋转坐标系下,两相之间将会存在6个耦合项,且要进行多次坐标变换,使控制器设计比较复杂且可靠性较低。而在αβ坐标系下,两相之间不存在耦合,无需进行解耦控制,且在αβ坐标系下采用比例—谐振(PR)控制器可以实现对交流信号的无静差调节,且能有效抑制电网谐波[13-14]。为了控制器在电网频率波动时仍能有较好的控制能力,本文在αβ坐标系下采用准PR控制器对系统进行控制,系统控制框图见附录A图A2。
为简化分析,假设直流侧电压不变,为Udc,有功和无功电流参考值也不变,由于开关频率远大于基波频率,可以采用开关平均模型,此时逆变器等效为一个比例环节Kpwm,只对电流内环进行分析,可得到αβ坐标系下电流内环控制框图如图1所示。

图1 逆变器电流内环控制框图Fig.1 Control block diagram of inverter inner current loop
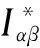
根据图1可以得到电流内环开环传递函数表达式为:

(1)
为了提高光伏并网系统的容量,大型光伏并网系统主要采用多逆变器并联结构[15],以内蒙古乌拉特后旗40 MW(峰值功率)大型光伏电站为例,并网系统结构图如附录A图A3所示,其中Z1为分裂变压器等效阻抗,Z2为主升压变压器等效阻抗,Zg′为光伏电站输出到大电网的阻抗。由于大型光伏并网系统的结构特点,各个光伏发电单元之间容易产生环流,影响逆变器的性能[16-17]。因此,为抑制环流,提高系统的稳定性,各光伏发电单元都采用相同的元件、结构及控制策略[18]。附录A图A3右边Zg′可以看成是n个nZg′相并联,由于当各个逆变器采用相同的元件、控制策略且出力相同时,各发电单元输出电压相同,母线a可以等效去除,从而Z2与nZg′相串联,同理,再将其转换到单个逆变器支路,从而得到相对于一台逆变器的等效电网阻抗:
Zg=2(nZg′+Z2)+Z1
(2)
可以看出,光伏电站容量越大,系统的等效电网阻抗值越大。因此,在下文的分析中将光伏电站容量的增加等效为电网阻抗的增加。可以看出,即使光伏电站到大电网的阻抗较小,当光伏电站容量n较大时,对于单个光伏发电单元而言的等效电网阻抗也很大。
2 电网阻抗的影响及抑制策略
2.1 电网阻抗对逆变器输出的影响
根据上面的分析,由电路理论知识可以得到,当实际并网电流能够跟踪参考电流,随着电网阻抗增大,由于并网电流和电网电压不变,电网阻抗上的压降增加,逆变器输出电压会下降。为方便分析,采用单位功率因数并网且忽略电网阻抗中的电阻分量,并网侧电压矢量图如图2所示,Vg为电网相电压峰值,Vl为电网电感上的压降,Vpv为逆变器输出电压。随着Vl增大,Vpv由a点变为b点,即逆变器输出电压下降。当电网阻抗足够大时,并网点电压会很小甚至为零。附录A图A4为电网电感Lg变化时逆变器输出电压Vpv的变化曲线图,从中可以看出,随着光伏电站容量不断增加,逆变器输出电压逐渐降低。当光伏电站容量增加使得等效电网电感为0.2 mH左右时,逆变器输出电压已降低到正常值的90%左右,若继续增加系统容量,逆变器输出电压将会持续降低,从电网吸收的无功功率逐渐增加,且过低的电压将会使系统因保护作用而跳闸。因此,在光伏电站扩容的情况下,很有可能会使系统运行点趋近c点,从而导致并网电能质量降低,甚至系统振荡而并网失败。

图2 并网侧电压矢量图Fig.2 Voltage vector diagram on grid-connected side
由于在只考虑电网电感的情况下,逆变器输出电压、电感上压降及电网电压满足直角三角形关系,因此逆变器输出电压可以表示为:
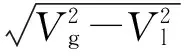
(3)
显然,在电网电压不变的情况下,电感上压降的上升将使得逆变器输出电压降低,在Vl≥Vg的情况下,式(3)将无解或为零解,此时系统出现不稳定现象。在极限运行状态时,电网电压等于电感上的压降,从而可以得到电网电感的表达式为:

(4)
式中:ω为基波角频率;I为并网相电流峰值;Lgr为系统稳定临界电网电感。
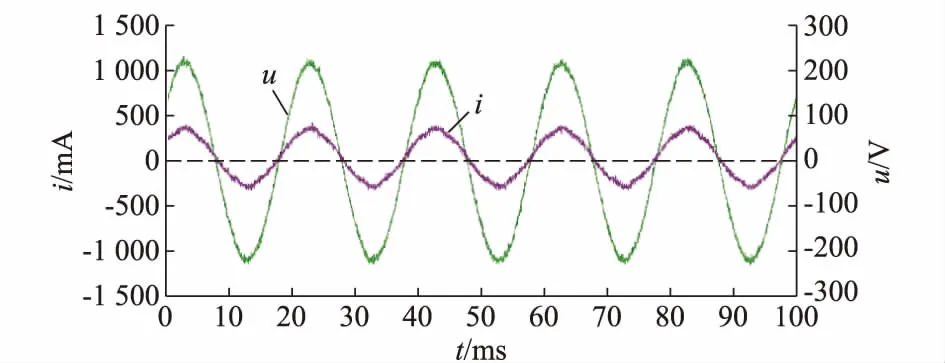
当Lg≥Lgr时,系统不稳定,出现振荡现象。当Lg (5) 式中:L1为分裂变压器低压侧及传输线路等效电感;L2为分裂变压器高压侧及传输线路等效电感;Lg′为光伏电站输出到大电网的等效电感。 然而,由于电网阻抗相当于等效增大电网侧滤波电感L2的值[19-20],从电流内环开环传递函数(详见附录A图A5)可以看出,随着电网阻抗的增加,电流内环的截止频率逐渐降低,系统的相位裕度和幅值裕度也逐渐降低,逆变器输出电压由振荡趋于稳定的时间越来越长,并网电能质量逐渐降低。 由上面的分析可知,对于大型光伏电站,随着光伏电站容量的逐渐增大,即使电网阻抗较小也会对光伏电站产生很大的影响,对于大型光伏电站中单个逆变器并网系统而言,随着电站容量的不断增加,等效电网阻抗的值要远大于实际的电网阻抗。会使得逆变器输出电压过低,波形畸变严重,甚至使系统出现持续振荡现象从而直接不能运行。为了避免因系统容量增加而导致的并网失败现象的发生,提高并网电压稳定性和并网电能质量,本文采用反馈控制策略,将电网阻抗环节进行等效变换,消除电网阻抗对于并网输出电压的影响,如2.1节式(4)所示,在电网电感Lg≥Lgr时,对于电流内环设计良好的逆变器而言,电流内环控制系统是稳定的,对于500 kW逆变器而言,当Lg=0.46 mH时,电流内环奈奎斯特曲线见附录A图A6,显然系统是稳定的,而由2.1节分析可知,逆变器输出电压无解从而造成系统的不稳定。此时,传统基于电流内环改善电网阻抗的方法将会显示出明显的不足,不能保证逆变侧电压的稳定性,基于此种情况,本文通过反馈策略自动调节系统输出容量,从而保持系统的稳定性,改善并网电能质量。由于是在电流内环控制框图的基础上进行的等效变换,因此对于电网阻抗对电流内环控制性能的影响也具有很好的抑制效果。 如图3所示,当只考虑电网阻抗感性分量Lg时,LCL滤波器电网侧等效电感为L2+Lg。为了消除电网电感的影响,滤波器网侧滤波电感阻抗值可以表达为式(6)的形式,对其进行等效变换,在原有的电流内环控制框图的基础上引入两路并网电流反馈,并将其等效变换到控制回路,所得反馈增益分别为H1和H2,如式(7)和式(8)所示。 (6) (7) (8) 图3 电网电感变化时电流开环传递函数的框图Fig.3 Block diagram of open-loop transfer function when grid impedance varies 按照以上分析,本文在MATLAB/Simulink仿真软件中搭建了500 kW光伏并网系统,系统参数见附录B表B1所示。a相并网电压和电流波形如附录B图B1所示,并网电流快速傅里叶变换(FFT)分析结果见附录B图B2。可以看出,当不考虑电网阻抗时三相并网电流能够很好地跟踪参考电流且满足并网要求。 在原有模型的基础上增加电网阻抗,当Lg为0.2 mH时,并网逆变器输出电压和电流波形如附录B图B3所示。从图B1和图B3可以看出,此时虽然增大了电网阻抗,但由于电流闭环控制的作用使得并网电流基本不受影响,仍能很好地跟踪参考,但是为了满足并网侧稳态三角形的关系,并网电压会在一定程度上降低,与之前理论分析一致。当将Lg增大到式(3)所算出的极限值时,根据附录B图B4,可以看出此时并网电压已经降为零,但由上面的分析可知,系统并不能在该状态下稳定运行,如图所示,在0.1 s左右时系统开始进入振荡状态。当继续增大电网阻抗使得Lg=1 mH时三相并网电流和电压波形如附录B图B5所示,此时单位功率因数控制不可能实现,系统进入非正常控制状态,并网电流和电压出现振荡且波形严重畸变,已完全不能满足并网要求。 为了使系统容量变大后,并网系统能够正常运行且保持较好的并网电能质量,消除电网阻抗对并网点电压的影响,采用本文提出的反馈策略。从附录B图B6可以看出并网电压维持不变且并网电流为正弦波,对并网电流进行FFT分析,如附录B图B7所示,可以看出并网电流总谐波畸变率小于5%,满足并网要求。但是由于电流反馈系数的存在,相当于将实际电流等效变为参考值的(L2+Lg)/L2倍。系统的开环传递函数的波特图如附录B图B8所示,可以看出系统具有良好的相位裕度和幅值裕度,截止频率也满足设计要求,根据系统频域指标与时域指标的换算关系,系统具有良好的动态性能。保持电网阻抗不变,进一步改变系统的电流参考值,在0.5 s时将电流增大一倍,由附录B图B9可以看出系统输出电压保持不变,电流在0.5 s时能很好地跟踪参考电流。 为进一步验证阻抗等效变换的正确性,增加说服力,对两台500 kW逆变器并联系统进行仿真验证。相比于一台逆变器并网时电网阻抗为1 mH的情况,根据上述变换原则,此时电网阻抗为0.5 mH。仿真结果如附录B图B10所示,ia1为一台逆变器输出的电流,ia2为两台逆变器总的并网电流,ua为并网电压。当逆变器不采用本文所述反馈策略时,如附录B图B10(a)所示,由于电网阻抗的作用,并网系统不稳定。当采用本文所述反馈策略时,如附录B图B10(b)所示,在原有的电网阻抗条件下,并网电压和电流保持稳定,并网系统正常运行。显然,分析电网阻抗对于并网电压的影响时,不管是将电网阻抗等效到单台逆变器并网的情况,还是保持原有的多机并联系统并网、不进行等效的情况,分析结果是相同的。 根据以上设计原则及步骤,以5 kW光伏并网系统为例进行实验验证,直流侧电源采用AGP1010提供700 V直流电压,电网电压有效值为220 V。逆变器采用CCS050M12CMC集成模块,并由集成驱动模块CGD15FB45P驱动,控制芯片采用DSP/TMS320F28335。LCL滤波器参数为:L1=5.5 mH,L2=1 mH,C=20 μF。PR控制器参数为:kp=0.047 86,kr=10.314 2,wc=3.14,w0=314,其中kp和kr为比例系数,wc为带宽频率,w0为谐振频率。电容电流有源阻尼系数kc=0.097。 首先,不采用本文所提出的反馈控制策略,根据式(4),当电网电感为90 mH时,a相电压和电流波形如图4所示,显然,传统的控制方式使得逆变器输出电压无解,导致系统振荡,且打破图2所示限制,进入非单位功率因数状态。采用本文提出的反馈控制策略,等效抵消电网阻抗对于控制的影响之后,并网电压和电流波形如图5所示。可以看出,并网电压能够稳定,但是由于主电路中电网阻抗的影响,并网电流下降到300 mA左右,并网电压和电流实现同相,并网电能质量得到明显改善。 图4 当Lg=90 mH时a相并网电压和电流波形图Fig.4 Grid-connected voltage and current waveforms of Phase a when Lg=90 mH 图5 改善后的a相并网电压和电流波形图Fig.5 Improved grid-connected voltage and current waveforms of Phase a 本文以500 kW光伏并网逆变器为例,针对大型光伏并网系统的结构特点,考虑电网阻抗的影响,将电网阻抗对大型光伏电站的影响等效化为对于大型光伏电站中单个光伏并网逆变器的影响,证明了光伏电站容量的增加会导致逆变器的等效电网阻抗增加。大的电网阻抗一方面会降低电流内环控制系统的稳定裕度,使系统的调节时间变长,并网电能质量降低,另一方面会使交流侧并网逆变器输出电压无解而导致系统不稳定。然而,光伏电站的大量扩容及出力的巨大增加都会导致电网阻抗的值出现很大的跃升,从而使系统直接出现振荡不稳定现象进而导致并网失败。 针对此情况,本文提出的控制策略旨在通过自动调节系统输出容量,保证在较大的电网阻抗情况下并网电压的稳定及较好的并网电能质量。显然,在大电网阻抗条件下,系统的稳定运行及良好的并网电能质量是以牺牲系统部分输出功率为代价的。而由本文分析可知,电网阻抗对于电压稳定的影响受逆变器输出功率因数的影响较大,在非单位功率因数并网的条件下,具有更大的稳定范围,因此下一步将结合逆变器输出有功和无功控制,抑制电网阻抗对于电压稳定性的影响。 附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。 [1] 国家能源局,太阳能利用十三五发展规划征求意见稿[EB/OL].[2017-02-06].http://www.aski.com/news/change/2015/12/30/146 53hmi2_6.shtml. [2] LISERRE M, TEODORESCU R, BLAABJERG F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values[J]. IEEE Trans on Power Electronics, 2006, 21(1): 263-272. [3] LUIS AGORRETA J, BORREGA M, LOPEZ J, et al. Modeling and control ofN-paralleled grid-connected inverters with LCL filter coupled due to grid impedance in PV plants[J]. IEEE Trans on Power Electronics, 2011, 26(3): 770-785. [4] 张密.大型光伏并网系统谐振现象分析[D].重庆:重庆大学,2014. [5] YE Qing, MO Ran, SHI Yanjun, et al. A unified impedance-based stability criterion (UIBSC) for paralleled grid-tied inverters using global minor loop gain (GMLG)[C]// IEEE Energy Conversion Congress and Exposition (ECCE), September 20-24, 2015, Montreal, Canada: 5816-5821. [6] 杨明.大型光伏电站逆变器并网控制策略及稳定性分析[D].重庆:重庆大学,2014. [7] 张兴,余畅舟,刘芳,等.光伏并网多逆变器并联建模及谐振分析[J].中国电机工程学报,2014,34(3):336-345. ZHANG Xing, YU Changzhou, LIU Fang, et al. Modeling and resonance analysis of multi-paralleled grid-tied inverters in PV systems[J]. Proceedings of the CSEE, 2014, 34(3): 336-345. [8] 艾欣,韩晓男,孙英云.大型光伏电站并网特性及其低碳运行与控制技术[J].电网技术,2013,37(1):15-23. AI Xin, HAN Xiaonan, SUN Yingyun. Grid-connection characteristics of large-scale photovoltaic power station and its low-carbon operation and control technology[J]. Power System Technology, 2013, 37(1): 15-23. [9] 张兴,曹仁贤.太阳能光伏并网发电及其逆变控制[M].北京:机械工业出版社,2011. [10] JALILI K, BERNET S. Design of LCL filters of active-front-end two-level voltage-source converters[J]. IEEE Trans on Industrial Electronics, 2009, 56(5): 1674-1689. [11] 赵强松,叶永强,徐国峰.分布式发电系统中并网逆变器的新型有源阻尼策略[J].电力系统自动化,2015,39(14):140-144.DOI:10.7500/AEPS20141208009. ZHAO Qiangsong, YE Yongqiang, XU Guofeng. A novel active damping control scheme for grid-connected inverter in distributed power generation systems[J]. Automation of Electric Power Systems, 2015, 39(14): 140-144. DOI: 10.7500/AEPS20141208009. [12] 杨淑英,张兴,张崇巍,等.LCL滤波电压源并网逆变器多环控制策略设计[J].电力系统自动化,2011,35(5):66-70. YANG Shuying, ZHANG Xing, ZHANG Chongwei, et al. Strategy design of multiple feedback loop control for grid-connected voltage source inverter with LCL filter[J]. Automation of Electric Power Systems, 2011, 35(5): 66-70. [13] 冯玉.三相光伏并网系统的研究[D].重庆:重庆大学,2011. [14] 陈炜,陈成,宋战锋,等.双馈风力发电系统双PWM变换器比例谐振控制[J].电工技术学报,2009,29(15):1-7. CHEN Wei, CHEN Cheng, SONG Zhanfeng, et al. Proportional-resonant control for dual PWM converter in doubly fed wind generation system[J]. Transactions of China Electrotechnical Society, 2009, 29(15): 1-7. [15] CAI Hui, ZHAO Rongxiang, YANG Huan. Study on ideal operation status of parallel inverters[J]. IEEE Trans on Power Electronics, 2008, 23(6): 2964-2969. [16] CHENG Y J, SNG E K K. A novel communication strategy for decentralized control of paralleled multi-inverter systems[J]. IEEE Trans on Power Electronics, 2006, 21(1): 148-156. [17] ITKONEN T, LUUKKO J, SANKALA A, et al. Modeling and analysis of the dead-time effects in parallel PWM two-level three-phase voltage-source inverters[J]. IEEE Trans on Power Electronics, 2009, 24(11): 2446-2455. [18] 杨明,周林,张东霞,等.考虑电网阻抗影响的大型光伏电站并网稳定性分析[J].电工技术学报,2013,28(9):214-223. YANG Ming, ZHOU Lin, ZHANG Dongxia, et al. Stability analysis of large-scale photovoltaic power plants for the effect of grid impedance[J]. Transactions of China Electrotechnical Society, 2013, 28(9): 214-223. [19] 周林,张密,居秀丽,等.电网阻抗对大型并网光伏系统稳定性影响分析[J].中国电机工程学报,2013,33(34):34-41. ZHOU Lin, ZHANG Mi, JU Xiuli, et al. Stability analysis of large-scale photovoltaic plants due to grid impedances[J]. Proceedings of the CSEE, 2013, 33(34): 34-41. [20] 陈新,张旸,王赟程.基于阻抗分析法研究光伏并网逆变器与电网的动态交互影响[J].中国电机工程学报,2014,34(27):4559-4567. CHEN Xin, ZHANG Yang, WANG Yuncheng. A study of dynamic interaction between PV grid-connected inverters and grid based on the impedance analysis method[J]. Proceedings of the CSEE, 2014, 34(27): 4559-4567. [21] 谢少军,季林,许津铭.并网逆变器电网阻抗检测技术综述[J].电网技术,2015,39(2):320-326. XIE Shaojun, JI Lin, XU Jinming. Review of grid impedance estimation for gird-connected inverter[J]. Power System Technology, 2015, 39(2): 320-326. AnalysisandImprovementStrategyforStabilityofLarge-scaleGrid-connectedPhotovoltaicSystemConsideringGridImpedance ZHANGQianjin,ZHOULin,XIEBao (State Key Laboratory of Power Transmission Equipment & System Security and New Technology (Chongqing University), Chongqing 400044, China) In the large-scale grid-connected photovoltaic (PV) system, the multi-inverter paralleled structure is used to improve the capacity of the system. According to this structure, as PV capacity is increased, the value of grid impedance can be equivalently enlarged with respect to a single PV power generation unit, which will directly result in failure of the control strategy for inverters, and finally a failure of connecting the PV system to grid. Based on the switch averaged model of the grid-connected PV system, this paper analyzes the influence of grid impedance on inverter output current and voltage. Then, by the output current feedback method, the automatic coordination between reference current and actual output current is realized to equivalently eliminate the influence of grid impedance on the stability of grid-connected voltage and the power quality, so as to guarantee the normal operation of system. Finally, the correctness of the theory is verified by the simulation analysis and experiment. This work is supported by National Natural Science Foundation of China (No. 51477021). large-scale grid-connected photovoltaic system; grid impedance; stability; power quality; virtual impedance 2017-04-13; 2017-07-14。 上网日期: 2017-09-08。 国家自然科学基金资助项目(51477021)。 张前进(1992—),男,通信作者,博士研究生,主要研究方向:光伏并网系统谐振稳定性分析与抑制及并网电能质量。E-mail: qianjin_zhang@foxmail.com 周 林(1961—),男,教授,博士生导师,主要研究方向:微网、光伏发电并网技术。E-mail: zhoulin@cqu.edu.cn 解 宝(1992—),男,博士研究生,主要研究方向:新能源发电光伏并网技术。E-mail: 1261889141@qq.com (编辑蔡静雯)2.2 电网阻抗抑制策略

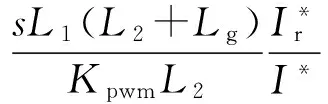




3 仿真与实验验证

4 结语

