基于混沌粒子群—高斯过程回归的饱和负荷概率预测模型
彭虹桥, 顾 洁, 胡 玉, 宋柄兵
(1. 上海交通大学电子信息与电气工程学院, 大数据工程技术研究中心, 上海市 200240; 2. 国家电网公司华东分部, 上海市 200120)
基于混沌粒子群—高斯过程回归的饱和负荷概率预测模型
彭虹桥1, 顾 洁1, 胡 玉1, 宋柄兵2
(1. 上海交通大学电子信息与电气工程学院, 大数据工程技术研究中心, 上海市 200240; 2. 国家电网公司华东分部, 上海市 200120)
饱和负荷预测能有效预估区域电网的发展方向和最终规模,为电网规划及电力市场中长期交易提供指导。针对饱和负荷预测不确定性强、时间跨度大的特点,文中采用基于高斯过程回归(GPR)的概率预测模型进行饱和负荷预测,并通过改进混沌粒子群算法(MCPSO)实现以和方差(SSE)最小为目标的模型超参数优化求解;在综合考虑饱和负荷影响因素随机性的基础上,建立了改进混沌粒子群—高斯过程回归(MCPSO-GPR)饱和负荷预测模型,并在多情景下利用上述模型进行饱和负荷预测,同时结合饱和判据得到多情景下饱和负荷的规模和时间。算例分析表明,所述模型不仅具有较高的预测精度,而且可增强预测的弹性。
饱和负荷; 负荷预测; 高斯过程回归; 混沌粒子群优化; 概率预测
0 引言
饱和负荷预测,作为电力系统远景规划的核心环节,包括最大负荷预测及电量预测。最大负荷易受到极端天气累积效应的影响而难以准确把握发展规律,因此对电量进入饱和状态的时间和规模进行预估[1-3]更具实践意义。研究区域电网电量的饱和时间及规模,既能为规划部门实现智能电网有序发展及区域能源平衡提供决策意见,又能为用户参与电力市场中长期交易提供数据分析支持。远景负荷时间跨度长、随机性强,其预测难度较大,因而开展饱和负荷概率预测对电网远景规划、区域能源平衡及中长期电力市场建设具有重要的应用价值。
目前,国内外针对饱和负荷预测的方法主要包括:时序外推法[4-5]、人均电量法[6]、系统动力学模型预测法[7]、空间负荷密度法[8]、用地仿真法[9-10]等。但随着地区人口规模限制、经济增速放缓及产业结构优化调整,部分发达地区用电量开始呈现一定的波动性及饱和态,传统的确定性建模方法对现阶段用电需求变化规律复杂、不确定因素多的演变特点考虑不全,预测精度受到限制。基于此,不少学者从主成分分析、多维度城市化因素及灵敏度校验等角度开展区域饱和负荷预测工作。文献[11]利用小波分析提取主成分及负荷的趋势分量进行饱和电量规模及时间的预测,但主成分与电量的单一关系未充分体现负荷发展受多种随机因素影响的复杂性。文献[12]采用层次分析法对多种城市化因素的影响度进行主观赋权重并依据模糊聚类实现预测,但权重值的主观性较强且用经典聚类方法对复杂经济环境下的饱和电量预测未必适用。文献[13]基于多维度饱和负荷预测模型,以偏导数的形式引入灵敏度对饱和负荷的波动性进行分析,但该指标是基于确定性模型提出的,未能全面考虑影响因素自身的随机性。
本文针对上述研究现状,采用高斯过程回归模型对饱和电量进行概率预测,该模型将电量视作多种影响因素共同作用下的随机过程,其预测结果具有概率意义;在此基础上,通过改进混沌粒子群算法求解了以预测偏差的最小和方差为目标的模型超参数优化问题;结合饱和电量影响因素的随机性,建立了改进混沌粒子群—高斯过程回归饱和电量预测模型,并在多情景下实现了上海市饱和电量的概率预测。
1 基于高斯过程回归的饱和负荷预测模型
1.1 高斯过程回归预测模型
高斯过程是随机过程的一种,适用于处理小样本、随机性强及含多维复杂因素的饱和负荷预测问题[14-16]。对于训练集D={(X,y)|X∈Rn×d,y∈Rn},其中X=[x1,x2,…,xn]T为一组训练输入变量,y=[y1,y2,…,yn]T为目标输出向量。输入变量的随机过程状态集合f(X)=(f(xi))服从n维联合高斯分布,因此f属于高斯过程,其概率函数用GP表示,可通过均值函数ρ(X)及协方差函数矩阵K(X,X′)确定[17],即
f(X)~GP(ρ(X),K(X,X′))
(1)
高斯过程回归模型将输入变量X与目标输出y之间的关系视作高斯过程f;把独立的白噪声ε考虑到f,则可建立标准高斯过程回归模型:
y=f(X)+ε
(2)

由于白噪声具有独立性,因此y同样属于高斯过程,即
(3)
根据贝叶斯原理,在给定的训练集D内,建立y的先验分布:
(4)
则对测试样本{(x*,y*)|x*∈Rd,y*∈R},根据高斯过程的性质,训练样本的目标输出y与测试样本输出y*服从联合高斯分布:
(5)
式中:K(X,X)=(k(xi,xj))为训练输入变量X的n×n阶协方差函数矩阵,k(xi,xj)为核函数;K(X,x*)=(k(xi,x*))为训练输入变量X与测试输入变量x*的n×1阶协方差函数矩阵;K(x*,x*)=k(x*,x*)为测试输入变量x*自身的协方差。
利用贝叶斯后验概率公式,在给定测试输入变量x*与训练集D*的条件下,对应的输出y*满足:
(6)

则高斯过程回归预测模型为:
(7)
cov(y*)=K(x*,x*)-

(8)
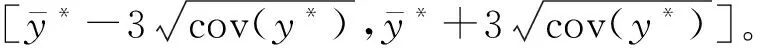
1.2 模型超参数求解的优化问题
建立高斯过程回归模型的难点是模型超参数的求解,而模型的超参数主要存在于协方差函数及白噪声中;因此为求解模型超参数,首先要确定协方差函数的具体形式。
高斯过程的协方差函数满足Mercer定理,因此协方差函数等价于核函数k[17]。本文基于高斯过程回归模型进行饱和负荷预测,核函数的选择要满足负荷预测“近大远小”的原则[1],同时符合远景负荷单调发展趋势。基于此,选择平方指数核函数(squared exponential kernel function)作为协方差函数;该核函数通过输入变量之间的距离差描述两者的相关性,距离越近,相关性越大,且适用于处理增长趋势的回归预测问题[17],具体表达式为:
(9)

为求解模型超参数,本文通过高斯过程回归模型对样本进行训练及测试,以测试样本的目标输出及其预测值之间的最小和方差作为目标,设计优化模型对模型超参数进行求解,具体如下式所示:
(10)
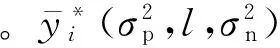
1.3 饱和电量概率预测模型
高斯过程回归模型应用于饱和电量预测的基本思路为:将电量及其影响因素的部分历史数据作为训练样本,影响因素的剩余历史数据作为测试样本,二者共同输入至高斯过程回归模型,通过滚动预测得到电量剩余历史数据的预测值并求解式(10)的优化问题,得到最优超参数;通过电量饱和判据[5](详见附录A表A1),并结合未来饱和电量影响因素的规划数值,建立饱和电量概率预测模型。具体的模型表达式如下:

(11)
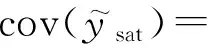
(12)

2 模型超参数优化问题求解算法
求解模型超参数常用方法为共轭梯度法,然而由于高斯过程回归模型较为复杂,优化问题式(10)的目标函数凹凸性无法直观判断,而共轭梯度法作为传统凸优化方法的一种,未必适用于超参数的优化求解;同时该方法过于依赖初值,容易陷入局部最优[17],并且不适用于含非线性约束条件优化问题式(10)的求解。其次,本文将高斯过程回归模型应用至饱和电量预测中,最优超参数的求解直接影响饱和电量预测模型的精度,即优化结果越好,预测精度越高。基于此,本文提出改进混沌粒子群优化 (modified chaotic particle swarm optimization)算法对超参数优化问题进行求解。
2.1 带极值变异的混沌粒子群优化算法基本原理
混沌粒子群算法的基本思想是将混沌特性引入到粒子的运动中,利用混沌动力系统的遍历性及轨迹规律性进行搜索,以拓宽粒子的搜索范围、增强收敛性能和提高收敛速度;但由于混沌序列具有初值敏感性,寻优效果并不理想。本文参考混沌蚁群动力学方程[18],提出带极值变异的混沌粒子群优化算法,以克服基本粒子群算法容易陷入局部最优[17]、混沌特性对初值敏感[18]的缺陷。具体改进如下所示。
步骤1:引入极值变异因子,使得粒子在个体最优位置及群体最优位置长时间停滞而发生变异,避免粒子出现早熟,提高算法跳出局部最优解的能力。
步骤2:建立混沌控制机制,改善混沌对初值的敏感性及拓宽粒子的搜索范围。则带极值变异的混沌粒子群系统动力学模型描述如下,
(13)
(14)
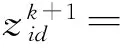
(15)
(16)

2.2 混沌控制机制
基于所述算法按混沌与稳定交替运动趋向全局的思想,迭代初期,利用基本粒子群优化算法初期快速收敛的特点[19],暂不引入混沌变量,改善引入混沌前粒子位置的初值;迭代中后期,当粒子稳定时,引入混沌变量,避免早熟;粒子运动时,撤去混沌变量,同时让粒子位于个体历史最优位置,结合极值变异因子,加速向最优收敛。
为判定粒子稳定与否,引入标志式(17),则混沌变量的确定过程如图1所示。
(17)

图1 混沌变量确定方法流程Fig.1 Flow chart of chaotic variable determination
2.3 超参数优化求解
将上述改进混沌粒子群优化算法应用至高斯过程回归模型的超参数优化问题的求解中,具体过程如下所示。
步骤1:以和方差作为适应度,根据超参数约束条件,初始化粒子群信息,如飞行速度、当前位置等。
步骤2:将超参数速度及位置信息,结合训练样本及影响因素的测试样本输入至高斯过程回归模型,依据式(7)及式(9)对负荷值的测试样本进行滚动预测,并计算粒子的适应度。
步骤3:更新粒子个体位置最优值及群体位置最优值,并判断群体最优适应度是否满足要求。若满足,则迭代结束,否则转步骤4。
步骤4:依据式(11)—式(14)更新粒子的速度及位置信息,转步骤2。
具体的算法流程图如图2中的③所示。

图2 改进混沌粒子群-高斯过程回归预测模型流程Fig.2 Flow chart of modified chaotic particle swarm optimization-Gauss process recursive forecasting model
确定高斯过程回归模型的超参数后,在考虑未来影响因素不确定性的基础上,结合饱和判据,可建立改进混沌粒子群—高斯过程回归饱和负荷概率预测模型。
3 饱和负荷预测的基本步骤
根据连续3年用电负荷增长率<2%,初步确定负荷进入饱和阶段的时间点,并对典型地区及国家在相应时间点下社会经济及电力发展特征的指标进行分析,得到附录A表A2所示的指标特征体系,并通过整合得到附录A表A1的饱和判据。基于此,饱和负荷预测的基本步骤如下。
步骤1:饱和时间点预测。在考虑未来影响因素不确定性的基础上,利用改进混沌粒子群—高斯过程回归模型对区域负荷进行外推预测,并确定附录A表A1中其他非负荷性质指标满足界定条件的时间点,取其中的最大年份作为饱和时间点。
步骤2:饱和负荷规模预测。根据上述饱和时间点的预测结果找到改进混沌粒子群—高斯过程回归模型外推至对应年份得到的负荷量规模的置信区间,并作为区域饱和负荷的概率预测结果。
具体步骤如图3所示。

图3 饱和电量预测基本步骤Fig.3 Basic steps for saturated electricity consumption forecasting
4 算例分析
[20-21]对中长期电力需求发展主要因素的分析(见附录A表A3),选取国内生产总值(2010年可比价,下同)、人口规模及三产占比作为电量的影响因素整体考虑。将改进混沌粒子群—高斯过程回归模型应用于上海市饱和电量预测问题中,通过对比,从预测精度及收敛性2个角度验证所述模型的有效性;其次,对未来影响因素进行不确定性建模,并结合饱和判据(见附录A表A1)在多情景下实现上海市饱和电量概率预测。
4.1 改进混沌粒子群—高斯过程回归预测模型有效性验证
选取上海市1978—2010年电量及上述影响因素的历史数据(见附录A表A4)构成训练样本,将2011—2015年的数据作为测试样本;首先对各影响因素按最大值归一化处理,以消除量纲差异,便于将多个影响因素作为整体而设置情景;其次通过改进混沌粒子群算法求解优化问题式(10),获得高斯过程回归模型的超参数。由于超参数在远景负荷预测中主要起控制相关性的作用,因此范围的选取要合理,本文启发式地设置a,b,c分别为400,5,100;并以相对误差(relative error)γRE及均方误差(mean square error)γMSE作为评价模型预测精度的标准。

(18)
(19)
根据上述预测精度评价标准,将训练样本及影响因素的测试样本作为改进混沌粒子群—高斯过程回归模型的输入,得到2011—2015年上海市电量的预测值,并对比文献[22]提出的2种模型,得到2011—2015年上海市电量预测结果比较如表1和图4。
由表1可知,本文模型预测的最大相对误差仅为1.28%,MSE仅为101.0,远小于文献[22]提出的2种模型,表明本文模型在电量预测精度上有较大的提高。同时,由图4可直观看出,2014年上海市用电量出现明显下降,本文模型对电量波动情形具备一定的预测能力,并且预测精度更高。
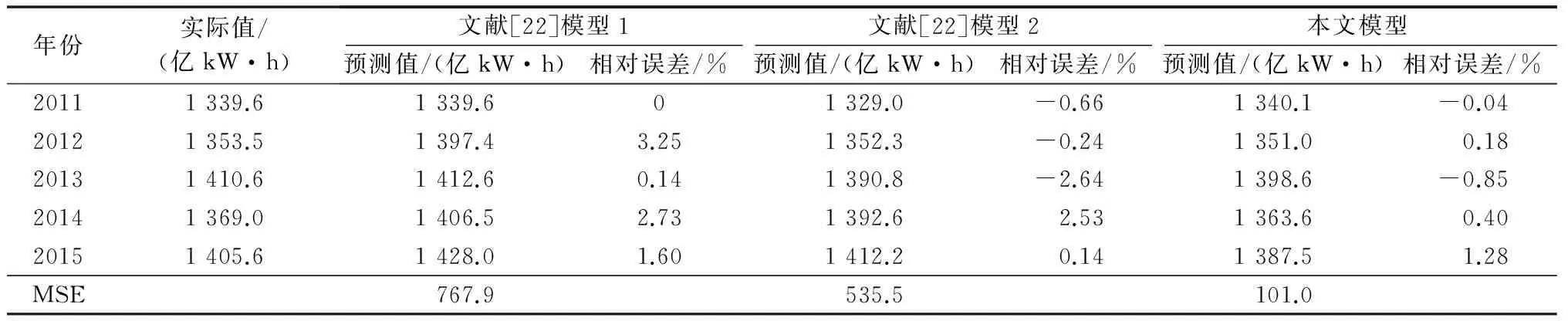
表1 三种模型的预测精度比较Table 1 Comparison of forecasting accuracy among three models

图4 三种模型预测结果对比Fig.4 Comparison of forecasting results among three models
其次,本文模型采用改进混沌粒子群算法求解超参数。设定粒子数为100,最大迭代次数为100,以收敛的平均迭代次数作为收敛速度、平均最小和方差作为适应度,与基本粒子群算法的比较结果如表2及图5所示。

表2 两种粒子群算法收敛性比较Table 2 Comparison of convergence of different particle swarm optimization

图5 两种算法适应度对比Fig.5 Comparison of fitness between two algorithms
由表2,本文采用的改进混沌粒子群算法相比于基本粒子群算法收敛速度更快,并且适应度更优,表明带极值变异的混沌粒子群算法具有较强的全局最优搜索能力及较快的收敛速度,适用于电量预测模型超参数的求解。
4.2 多情景下饱和电量的概率预测
经过模型有效性的验证,需要结合未来年份影响因素的规划值,才能利用改进混沌粒子群—高斯过程回归模型对上海市电量进入饱和阶段的时间及规模进行概率预测。但由于未来影响因素的规划数值(见附录A表A5)不完整,且未来影响因素具有较大的随机性,因此需要对影响电量的主要因素的规划值进行数据补全及不确定性处理。
1)数据补全

2)未来影响因素的不确定性建模
由于影响因素的规划值无法反映其未来发展的随机性,因此需要对未来影响因素进行不确定性处理。
首先通过Hodrick-Prescott滤波[23],提取影响因素历史数据的波动序列,记为XHP=[x1,HP,x2,HP,…,xn,HP]T,求解各影响因素的最大相对波动率γd:

(20)
式中:下标d具体表示某个特定的影响因素,如人口、国内生产总值或三产占比。

通过计算得到,上海市人口、国内生产总值及三产占比的最大相对波动率分别为:3.2%,18%,8%。
此外,通过调研得到附录A表A2各个因素对未来电量发展的影响结果,结合历史波动序列间的演变规律 (如图6所示),可得人口及国内生产总值对电量发展起促进作用,而三产占比的提高则会减缓电量的发展。因此,根据上述未来影响因素的不确定性模型,将影响因素作为一个整体考虑,设定以下3个情景。
情景1:未来各年的人口及国内生产总值达到可能变化范围的最大值、三产占比处于变化范围的最小值。
情景2:国内生产总值、人口及三产占比按规划值平稳发展。
情景3:未来各年的人口及国内生产总值达到可能变化范围的最小值、三产占比处于变化范围的最大值。

图6 上海市电量及其主要影响因素波动序列Fig.6 Fluctuation sequence of Shanghai electricity and its main affecting factors
基于此,由上述饱和电量预测的基本步骤,将各情景下未来影响因素输入至改进混沌粒子群—高斯过程回归模型,在3种情景下对上海市饱和电量进行概率预测。饱和时间点的分析结果如表3所示,未来上海市的电量规模的概率预测结果如图7所示。

表3 多情景下上海市电量饱和时间点Table 3 Saturation time for electrical consumption in multi-scenarios in Shanghai

图7 上海市电量概率预测结果Fig.7 Probabilistic forecasting result of electrical consumption in Shanghai
通过饱和判据的分析及验证,在3种不同情景下上海市的用电量都将于2026年左右进入饱和阶段,表明上述3种影响因素共同作用下,整体的随机性波动对上海市的电量增长速度影响较小。根据本文选用的SE协方差函数,当相邻年影响因素取值接近时,后一年的电量预测值与前一年的电量值相差较小,因此,可推知电量增长趋于饱和主要是由于各影响因素的发展趋于停滞而导致的。
另一方面,未来影响因素的波动幅度对上海市电量饱和规模的影响较大;相应情景下上海市饱和电量规模概率预测结果如表4所示。

表4 多情景下上海市饱和电量规模的概率预测结果Table 4 Probabilistic forecasting results of saturated electrical scale in Shanghai based on multi-scenario analysis
结果表明,在按规划值平稳发展的情景下,有99.73%的把握认为上海市的饱和电量规模将落入[1 790,1 842]亿kW·h的区间内。同时,在各影响因素最大程度促进电量增长的情景下,饱和电量规模预计将达到1 957亿kW·h,99.73%置信区间为[1 919,1 996]亿kW·h,高于平稳发展情景下的饱和电量规模;若在未来影响因素最大程度减缓电量增长的情景下,饱和电量规模的期望值将只能达到1 696亿kW·h,99.73%置信区间为[1 669,1 723]亿kW·h,低于平稳情景下的饱和电量规模。
5 结语
通过与文献[22]的模型进行预测精度及收敛性的分析对比,验证了本文模型的优越性。 在考虑饱和负荷影响因素不确定性的基础上,将本文模型应用于上海市饱和电量的概率预测,结果表明,考虑所用影响因素的整体不确定性波动,对上海市电量的增长速度影响较小,但对饱和电量的规模影响较大。 提出多情景分析方法,获得3种情景下饱和电量概率预测结果,增强了本文模型的预测弹性,并能有效应用于未来复杂经济情景下的区域能源平衡预估及规划决策等。
值得注意的是,本文得到的上海市饱和电量预测结果属于阶段性的研究成果。下一步计划从电量与影响因素之间的耦合关系开展研究,以得到各因素对电量确切影响度的量化指标,进一步提高高斯过程回归模型应用于饱和电量预测的适应性。
附录见本刊网络版(http://www.aeps-info.com/aeps/ch/index.aspx)。
参考文献
[1] 康重庆,夏清,刘梅.电力系统负荷预测[M].北京:中国电力出版社,2007.
[2] 肖欣,周渝慧,张宁,等.城市电力饱和负荷分析技术及其应用研究综述[J].电力自动化设备,2014,34(6):146-152.
XIAO Xin, ZHOU Yuhui, ZHANG Ning, et al. Survey of saturated load analysis technology for urban power system and its application[J]. Electric Power Automation Equipment, 2014, 34(6): 146-152.
[3] JIA Y, LI S, TAN Y, et al. Improved parametric estimation of logistic model for saturated load forecast[C]// Power and Energy Engineering Conference, March 16, 2012, Shanghai, China: 1-4.
[4] 鲍正杰,李生虎,赵锋,等.饱和负荷预测中的改进Logistic算法[J].电力系统及其自动化学报,2014,26(11):7-11.
BAO Zhengjie, LI Shenghu, ZHAO Feng, et al. Improved logistic model for saturated load forecast[J]. Proceedings of the CSU-EPSA, 2014, 26(11): 7-11.
[5] 尚芳屹,杨宗麟,程浩忠,等.改进Verhulst模型在饱和负荷预测中的应用[J].电力系统及其自动化学报,2015,27(1):64-68.
SHANG Fangyi, YANG Zonglin, CHENG Haozhong, et al. Application of improved Verhulst model in saturation load forecasting[J]. Proceedings of the CSU-EPSA, 2015, 27(1): 66-68.
[6] 张建平,刘杰锋,陈屹东,等.基于人均用电量和人均用电负荷的饱和负荷预测[J].华东电力,2014,42(4):661-664.
ZHANG Jianping, LIU Jiefeng, CHEN Yidong, et al. Saturated load forecasting based on per capita electricity consumption and per capita electricity load[J]. East China Electric Power, 2014, 42(4): 661-664.
[7] 谭忠富,张金良,吴良器,等.中长期负荷预测的计量经济学与系统动力学组合模型[J].电网技术,2011,35(1):186-190.
TAN Zhongfu, ZHANG Jinliang, WU Liangqi, et al. A model integrating econometric approach with system dynamics for long-term load forecasting[J]. Power System Technology, 2011, 35(1): 186-190.
[8] 肖白,周潮,穆钢.空间电力负荷预测方法综述与展望[J].中国电机工程学报,2013,33(25):78-92.
XIAO Bai, ZHOU Chao, MU Gang. Review and prospect of the spatial load forecasting methods[J]. Proceedings of the CSEE, 2013, 33(25): 78-92.
[9] 梁锦照,夏清.基于标量场分析的远景负荷预测新方法[J].电力系统自动化,2009,33(17):91-95.
LIANG Jinzhao, XIA Qing. A new method of long-term load forecasting based on scalar field analysis[J]. Automation of Electric Power Systems, 2009, 33(17): 91-95.
[10] VASQUEZ-ARNEZ R L, JARDINI J A, CASOLARI R, et al. A methodology for electrical energy forecast and its spatial allocation over developing boroughs[C]// 2008 IEEE/PES Transmission and Distribution Conference and Exposition, April 21, 2008, Chicago, Illinois: 1-6.
[11] 李亦言,韩冬,严正,等.复杂城市化因素下的饱和负荷预测模型[J].电网技术,2016,40(9):2824-2831.
LI Yiyan, HAN Dong, YAN Zheng, et al. Saturated load forecasting model under complex urbanization characteristics[J]. Power System Technology, 2016, 40(9): 2824-2831.
[12] 李亦言,严正,冯冬涵.考虑城市化因素的中长期负荷预测模型[J].电力自动化设备,2016,36(4):54-61.
LI Yiyan, YAN Zheng, FENG Donghan. Mid/Long-term load forecasting model considering urbanization characteristics[J]. Electric Power Automation Equipment, 2016, 36(4): 54-61.
[13] 刘杰锋,程浩忠,韩新阳,等.多维度饱和负荷预测方法及其应用[J].电力系统及其自动化学报,2015,27(2):44-50.
LIU Jiefeng, CHENG Haozhong, HAN Xinyang, et al. Forecasting method and application of multi-dimensional saturated load[J]. Proceedings of the CSU-EPSA, 2015, 27(2): 44-50.
[14] 甘迪,柯德平,孙元章,等.基于集合经验模式分解和遗传-高斯过程回归的短期风速概率预测[J].电工技术学报,2015,30(11):138-147.
GAN Di, KE Deping, SUN Yuanzhang, et al. Short-term wind speed probabilistic forecasting based on EEMD and coupling GA-GPR[J]. Transactions of China Electrotechnical Society, 2015, 30(11): 138-147.
[15] ALAMANIOTIS M, CHATZIDAKIS S, TSOUKALAS L H. Monthly load forecasting using Gaussian process regression[C]// Mediterranean Conference on Power Generation, Transmission, Distribution, and Energy Conversion: Medpower, November 2, 2014, Athens, Greece.
[16] YAN W, QIU H, XUE Y. Gaussian process for long-term time series forecasting[C]// IEEE International Joint Conference on Neural Networks, June 14, 2009, Atlanta, GA, USA: 3420-3427.
[17] RASMUSSEN C E, WILLIAMS C K I. Gaussian processes for machine learning[M]. Massachusetts: MIT Press, 2006.
[18] LI Lixiang, YANG Yixian, PENG Haipeng, et al. An optimization method inspired by “chaotic” ant behavior[J]. International Journal of Bifurcation & Chaos, 2011, 16(16): 2351-2364.
[19] KENNEDY J, EBERHART R. Particle swarm optimization[M]. New York: Springer, 2014.
[20] 华东区域“十三五”及中长期电力需求发展趋势研究[R].上海:中国电力工程顾问集团华东电力设计院,2015.
[21] 李智勇,陈志刚,徐政,等.中国全社会用电量增长主导因素辨识[J].电力系统自动化,2010,34(23):30-35.
LI Zhiyong, CHEN Zhigang, XU Zheng, et al. Identification of dominant factors in China’s power consumption growth[J]. Automation of Electric Power Systems, 2010, 34(23): 30-35.
[22] 周德强.改进的灰色Verhulst模型在中长期负荷预测中的应用[J].电网技术,2009,33(18):124-127.
ZHOU Deqiang. Application of improved gray Verhulst model in middle and long term load forecasting[J]. Power System Technology, 2009, 33(18): 124-127.
[23] POLONI F, SBRANA G. Multivariate trend-cycle extraction with the Hodrick-Prescott filter[J/OL]. Statistics, 2015. [2016-12-23]. http://pages.di.unipi.it/fpoloni/publications/files2/PolS15hp_arxiv.pdf.
ForecastingModelofSaturatedLoadBasedonChaoticParticleSwarmandOptimization-GaussianProcessRegression
PENGHongqiao1,GUJie1,HUYu1,SONGBingbing2
(1. School of Electronic Information and Electrical Engineering, Research Center for Big Data Engineering and Technologies, Shanghai Jiao Tong University, Shanghai 200240, China; 2. State Grid Corporation of East China, Shanghai 200120, China)
Saturated load forecasting could effectively estimate future direction and final scale of the regional power grid, providing guidance for planning and mid/long-term transactions of the power market. Firstly, a probabilistic forecasting model based on Gaussian process regression (GPR) is adopted for saturated load forecasting, aiming at its characteristic of strong uncertainty and large time span. Secondly, the optimal solution of model hyper-parameters with the objective of minimizing the sum of squares due to errors (SSE) is realized by a modified chaotic particle swarm optimization (MCPSO) presented. In consideration of the randomness of the factors influencing the saturated load, a saturated load forecasting model based on modified chaotic particle swarm optimization-Gaussian process regression is proposed. Thirdly, in multi-scenarios using the above model while taking saturation criterion into account could forecast the saturated load and obtain multi-scenario scale and time-point. Finally, case studies show that this model not only has high precision, but also enhances the elasticity of forecasting results.
This work is supported by National Key Research and Development Program of China (No. 2016YFB0900101).
saturated load; load forecasting; Gaussian process regression (GPR); chaotic particle swarm optimization; probabilistic forecasting
2017-01-19;
2017-04-19。
上网日期: 2017-06-23。
国家重点研发计划资助项目(2016YFB0900101)。
彭虹桥(1993—),男,硕士研究生,主要研究方向:电力系统优化规划。E-mail: phq382316206@sjtu.edu.cn
顾 洁(1971—),女,通信作者,博士,副教授,主要研究方向:电力市场及电力系统优化规划。E-mail: gujie@sjtu.edu.cn
胡 玉(1995—),女,主要研究方向:电力市场、电力系统规划。E-mail: 285242198@qq.com
(编辑顾晓荣)

