基于尺度效应的过程安全事故概率估计

胡瑾秋，郭家洁

（中国石油大学（北京）油气资源与工程国家重点实验室，机械与储运工程学院，北京 102249）

基于尺度效应的过程安全事故概率估计

胡瑾秋，郭家洁

（中国石油大学（北京）油气资源与工程国家重点实验室，机械与储运工程学院，北京 102249）

为提高过程安全事故概率估计方法的适用性，需在基本事件阶段考虑工艺偏差的传播过程。提出基于尺度效应的过程安全事故概率估计方法，从工艺偏差角度入手，建立了新的基本事件求解模型。引入了多尺度思想，在大尺度上，考虑人因失误对工艺偏差的影响，修正基本事件概率。选用模糊Petri网模型进行事故概率估计。最后通过冲塔事故案例分析验证模型，结果表明：人的参与对工艺偏差概率具有较大影响，所提方法比较符合实际工况，更适用于过程安全。由于概率估计是基于统计的数据求取偏差概率，避免了直接对计算参数进行设定的主观性。

多尺度；过程系统；事故概率；工艺偏差；人因失误；安全

引 言

随着近期复杂化工过程重大事故频发，提高安全性以减少重大事故的发生意义重大[1]。化工过程安全事故大多由于系统的“变化”引起，如液位偏高、流量过大、管线裂纹等。如果这些“变化”使系统的运行工况超出设计预期的安全范围，将出现系统故障。单一设备或工艺过程出现故障，极易借助系统单元之间的相互依存、相互制约关系，触发链锁效应，由一种故障引发出一系列故障链直至引起事故或灾难[2]。由此可见，研究分析工艺偏差传播过程造成的事故风险，确定事故概率估计方法，具有非常重大的意义。

目前就单一事故而言，如何进行事故风险分析，国内外的相关研究很多，有些研究成果也相对成熟。应用较为广泛的基于图论的风险分析方法主要有：事件树分析法[3-5]、Bow-tie分析法[6-7]、马尔可夫链分析法[8]、贝叶斯网络分析法[9-10]、Petri 网分析法[11-13]；基于数理统计的风险分析方法有：神经网络法[14]、蒙特卡罗法[15]、灰色理论动态风险评价法[16]、危险指数评价法[17]。

以上这些方法在事故概率估计方面相对成熟。但就基本事件考虑得比较杂乱，从零件故障、工艺偏差到人因失误不等，且数据都是通过数据库所得，并不能很好地反映过程安全的研究实况。并且当研究尺度增大时，如何综合考虑“偏差”之间的关联、人员参与等一系列因素对“偏差”的影响，无论是国内还是国外，相关的研究与实践并不多。为此，本文提出了基于尺度效应的过程安全事故概率估计方法，该方法从过程安全事故风险的多尺度属性入手，小尺度上的基本事件全部采用工艺偏差变量，偏差传播至大尺度上形成事故采用Petri网，建立过程安全事故概率计算模型，可用于石油石化企业安全评价。

1 基本理论

1.1 相关定义

1.1.1 尺度划分 在安全科学领域，研究人员已认识到自然灾害的空间层次特点并对自然灾害的尺度进行划分[18]。生态学上也给出了尺度划分依据和标准[19-20]。过程安全领域也有对尺度划分的研究[21]。结合生态学尺度划分依据和过程安全尺度划分先例，基于催化裂化装置的特点，将其定性分为几个尺度：工艺参数尺度、事故尺度、车间尺度、化工园区尺度。

1.1.2 尺度效应 由于空间尺度的不同，灾害风险因子特征和表征方式、方法的差异而导致的数据精度，风险表征、分级和风险地图特征不同的现象，称为灾害风险尺度效应[22]。由此，狭义过程安全的尺度效应定义为：由于空间、时间尺度的不同，工艺参量偏差的传播而导致的事件概率表征不同的现象，称为过程安全尺度效应。例如，若从部件增加到单元层面上增加幅度，人员的操作、参量偏差的传递均能影响工艺偏差概率的估计。

1.1.3 工艺偏差概率 化工过程事故通常起源于异常扰动。异常扰动会造成工艺变量偏离正常区域，从而触发 H/L报警[23]。从变量偏离正常区域触发H/L报警即为产生一次H/L偏差。该报警发生概率反映了相应变量受干扰出现异常的概率。而在固定时间段内，变量处于报警状态时间（即总恢复时间）反映了该变量触发H/L报警概率的大小。因此，釆用工艺变量在一段时间长度内的总恢复时间与该段时间的比值作为关键变量发生 H/L报警概率估计值，即H/L偏差概率。

1.2 人因失误模型理论

1.2.1 THERP模型理论 20世纪 80年代初，THERP（人因失误率预测技术）由 Swain等[24]人因分析专家提出。THERP模型主要基于人因可靠性分析(HRA)事件树模型。它将人因事件中涉及的人员行为按事件发展过程进行分析，并在事件树中确定失效途径后进行定量计算。人因可靠性事件树描述人员进行操作过程中一系列操作事件序列；它按时间为序，以两态分支扩展。其每一次分叉表示该系统处理任务过程的必要操作，有成功和失败两种可能途径[25]。因而某作业过程中的人因可靠性事件树可描述出该作业过程中一切可能出现的人因失误模式及其后果。对树的每个分枝赋予其发生的概率，则可最终导出作业成功或失败的概率。

1.2.2 HCR 模型理论 由于THERP模型主要是描述与时间无关的人因失误，而现代的人-机系统常常与人的认知判断有关，HCR法[26]就是为了评价运行班组未能在有限的时间内完成动作的概率而开发的。

HCR 的基本假设如下。

（1）它认为所有的人员动作的行为类别可以根据是否为例行的工作、程序书的情况及训练的程度等，分为技能型、规则型及知识型3种。

（2）它认为每一种行为类别的失误概率EP，仅与允许时间Mt和执行时间CT1/2的比值有关。根据此假设，HCR模式归纳得到式(1)

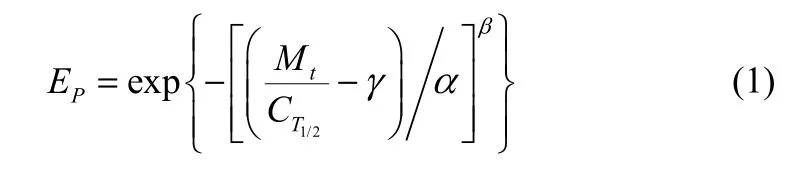
式中，Mt为操作员对突发事件反应时间的最大值；CT1/2为在具体的事件中，所有被测得的工作人员辨识所用时间的中值；α、β、γ是由数据归纳而得与行为类别有关的威布尔分布参数。

由于每个运行班组的执行时间可能因各类情况而有所不同，故在使用公式之前要用修正因子修正。在 HCR模式中所考虑的关键的行为形成因子有3个，训练(K1)、心理压力(K2)及人-机界面(K3)，K1、K2、K3的选取见文献[27]。修正的公式表示如下

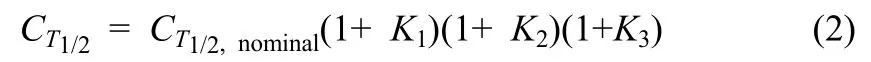
式中，CT1/2,nominal为一般状况的执行时间。

1.3 模糊Petri网理论

模糊Petri网（fuzzy Petri net，FPN）是在传统Petri网基础上结合模糊集理论形成的一种新的网络理论，用于对基于规则的系统进行建模与推理[28]。模糊Petri网既具有Petri网描述异步并发及图形表述的能力，又具有模糊系统的推理能力，使得对系统知识的表示更为简洁、清晰，对系统知识的分析、推理、测试以及决策支持也更加便捷。由于实际应用背景或相关技术的不同，不同学者根据实际需要给出过多种不同的模糊Petri网定义。

化工过程工艺偏差之间的相关关系不但具有模糊性而且具有传播性。因此，可以用模糊产生式规则来描述两者之间的模糊关系或传递关系。

这里将模糊 Petri网定义为一个 9元组：FPN=(P,T,D,IN,OUT,W,M,V,R)，其中

（1）P={p1,p2,…,pn}，表示库所集，pi表示其中的一个风险因子；

（2）T={t1,t2,…,tm}，表示变迁集，其中tj表示某一个风险发生的过程；

（3）D={d1,d2,…,dn}，表示命题集，与pi相互对应；

（4）IN表示的输入矩阵，∈{0,1}为逻辑量，当pi是tj的输入时，αij=1，当pi不是tj的输入时，αij=0(i=1,2,…,n;j=1,2,…,m)；

（5）OUT表示的输出矩阵，βij∈{0,1}为逻辑量，当pi是tj的输出时，βij=1，当pi不是tj的输出时，βij=0(i=1,2,…,n;j=1,2,…,m)；

（6）W表示命题库所pi的可信度集合，这里的可信度表示各风险因子的概率值，W(pi)={wi}(i=1,2,…,n)，wi在[0,1]区间；

（7）M(0)表示n×1阶的初始状态矩阵为库所pi的初始状态值，是从库所到一个[0,1]之间的实数值的映射，M(k)为发生了k次变迁后的状态矩阵；

（8）V表示规则变迁tj的可信度集合，这里表示各风险因子被触发的概率值，V(tj)={μj}(j=1,2,…,m)，μj在[0,1]区间；

2 基于尺度效应的事故概率估计模型

建立基于尺度效应的事故概率估计模型分为 3个阶段，如图1所示。

2.1 阶段1：数据的收集与处理

（1）准备工作。准备与所研究事故相关的材料，如PID图、工艺流程说明、HAZOP分析、操作规程、专家和有经验的员工参与意见。

（2）数据收集。根据现场的监测数据，收集与所研究事故相关的工艺参数报警指标，如详细记录各工艺变量偏差的信息，包括报警日期、报警时间、报警变量、变量描述、报警类型等信息。这些信息被存储在DCS系统的报警数据库中。考虑到报警泛滥，文中将一次持续时间为10 min以内报警泛滥造成的所有报警记为一次工艺偏差。

（3）数据处理。根据收集到的数据，需要简单处理得到，工艺变量偏离正常区域的时间总和（即恢复时间（RT）总和）。各工艺偏差中的第一次报警与最后一次报警的时间差近似作为恢复时间。一般以8 h（一个班组的工作时间）为单位时间段统计i个时间段各时间段内某偏差的总恢复时间（RT）。

2.2 阶段2：基本事件概率估计

图1 事故概率估计模型Fig.1 Accident probability estimation model

（1）小尺度工艺偏差概率估计

根据阶段1得到的数据，计算某工艺变量的H/L偏差概率t0

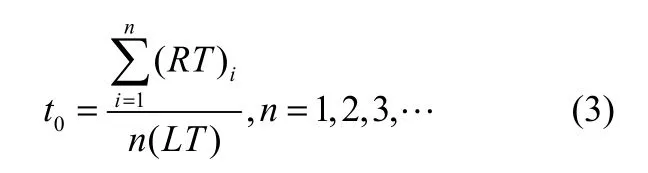
其中，n表示统计时间段个数，LT表示统计时间段长度，RTi表示变量在第i个时间段内的总恢复时间。根据式（3）及统计的历史数据，可得各工艺变量随统计时间段个数增加的H/L偏差概率的变化情况。随着统计时间段个数的增加，各工艺变量的H/L偏差概率值将基本稳定在某一极小的区间之内。若所求的连续5个H/L偏差概率值其相邻两个值之差均小于某一极小值，则取这5个值的平均值作为该工艺变量的H/L偏差概率。

（2）尺度效应下的修正因子——人因失误概率估计

建立 THERP+HCR 的模型：在事故诊断阶段，用 HCR 分析方法对该阶段可能的人员响应失效概率进行评价；而对在进行具体的干预操作行为中可能的失误用 THERP 分析方法及相关数据进行评价，两者相互补充，共同构成一个有机整体。

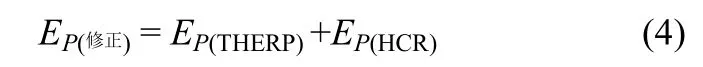
（3）大尺度工艺偏差概率估计

因为考虑了修正因子，所以大尺度上的工艺偏差概率为

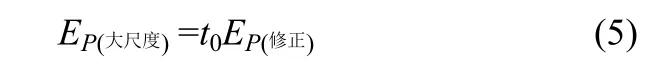
事实上，除人因失误外，BPCS作用机制、安全屏障等也会对工艺偏差概率这一数据产生较大影响，可作为修正因子。人的因素诱发的事故已成为化工企业最主要的事故源之一，本文使用人因失误来修正，暂时不考虑其他因素，多个因素作用的影响是继续研究的方向。

2.3 阶段3：模糊Petri网事故概率估计

令R为模糊产生式的规则集，R={R1,R2,…,Rn}，其中Ri为R中的第i个规则，则Ri定义为：ifpi,thenpk。其中，pi代表某工艺偏差；pk代表由pi可能触发的工艺偏差；wi为pi对这一规则的可信度（即为各工艺偏差的概率值），μi为这条规则被触发的可信度（即各工艺偏差被触发的概率值，由专家经验获得），且μi,wi∈[0,1]。pi到pk表示偏差的传播路径，体现了各工艺偏差间存在相关关系。

基于模糊 Petri网的控制因素及相关关系分析步骤如下。

（1）针对某一事故过程，首先辨识其在小尺度上存在的各种工艺偏差即与此事故相关的可以监测到的工艺变量报警记录；

（2）根据所辨识的化工过程工艺偏差和HAZOP分析，确定工艺偏差间的相关性和传播性，根据相关关系构造FPN模型，根据阶段2所得各工艺偏差概率和专家给出的各工艺偏差被触发的概率值分别确定初始状态矩阵M(0)及变迁可信度集合为库所pi的初始状态值；

（3）根据基本理论中所给的FPN定义可确定输入矩阵IN和输出矩阵OUT；

（4）进行模糊推理计算，初始状态k=0，当变迁可以发生时，计算变迁触发后的下一个状态，M(k+1)=M(k)⊕[VΔOUT][INTM(k)]；

（5）若M(k+1)=M(k)，或其中有元素值为0，令k=k+1，重复步骤（4）；若M(k+1)=M(k)，则推理结束，M(k)即为各库所的实际可信度集合，也是最终求得的各实际概率值。

3 案例分析

3.1 事件描述

催化裂化分馏过程（图 2）中，分馏塔结盐、分馏塔底液面超高或者分馏塔进料带水都会引起分馏塔汽液相负荷过大，进而导致分馏塔冲塔事故[29]。分馏塔冲塔，油气中的重组分携带到上部塔盘，会使汽油干点和柴油95%（或干点）超高；塔顶温度过高易引起富气带液，影响气压机运行，严重时发生塔盘结焦堵塞，危及安全生产；发生冲塔事故，油气溢流出来遇明火极易引发火灾爆炸事故。

以催化裂化生产装置中的分馏塔冲塔事故为例，分别从工艺变量级小尺度及事故级大尺度上进行控制因素尺度效应分析。

针对分馏塔冲塔事故发生过程，首先辨识其在不同尺度上存在的各种控制因素。在工艺变量级小尺度上，控制因素主要为不同工艺变量的工艺偏差，包括分馏塔搅拌蒸汽流量高报警、中段循环油返塔温度高报警、分馏塔顶循环回流量高报警、分馏塔顶温度高报警、分馏塔顶压力高报警、分馏塔中段油流量高报警、分馏塔底液位低报警等。在事故级大尺度上，需要考虑人因失误问题。

3.2 基本事件概率估计

3.2.1 小尺度工艺偏差概率估计 以工艺偏差——分馏塔搅拌蒸汽流量高报警为例，以8 h为单位时间段统计了 86个时间段各时间段内变量分馏塔搅拌蒸汽流量的总恢复时间（RT）。根据式（3）及统计的历史数据，随统计时间段个数增加，累计计算变量在一段时间长度内的总恢复时间与该段时间的比值，如图 3所示。通过计算发现，累计至第 55个时间段起，其后的连续5个比值其相邻两个值之差均小于某一极小值（这里设为0.001），则取这5个值的平均值作为该工艺变量的H/L偏差概率t0，可得

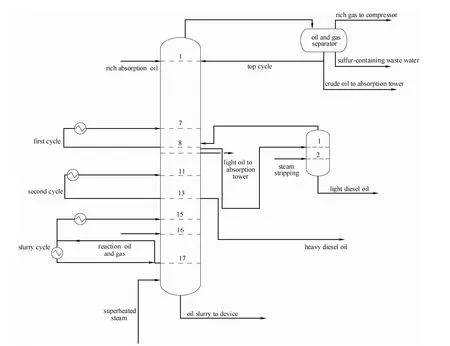
图2 分馏塔工艺流程Fig.2 Process flow chart of fractionating tower

从图3也可以看出，随着统计时间段个数的增加，H/L偏差概率基本稳定在0.11～0.125之间。

3.2.2 人因失误概率估计

（1）人员参与事件分析

① 操作员由塔搅拌蒸汽流量高报警进入 DEC规程即冲塔规程诊断阶段，失误概率EP1可认为非常小。

② 操作员由冲塔规程诊断进入冲塔确认阶段即A1规程，作出的降量并调节冷回流的判断，其

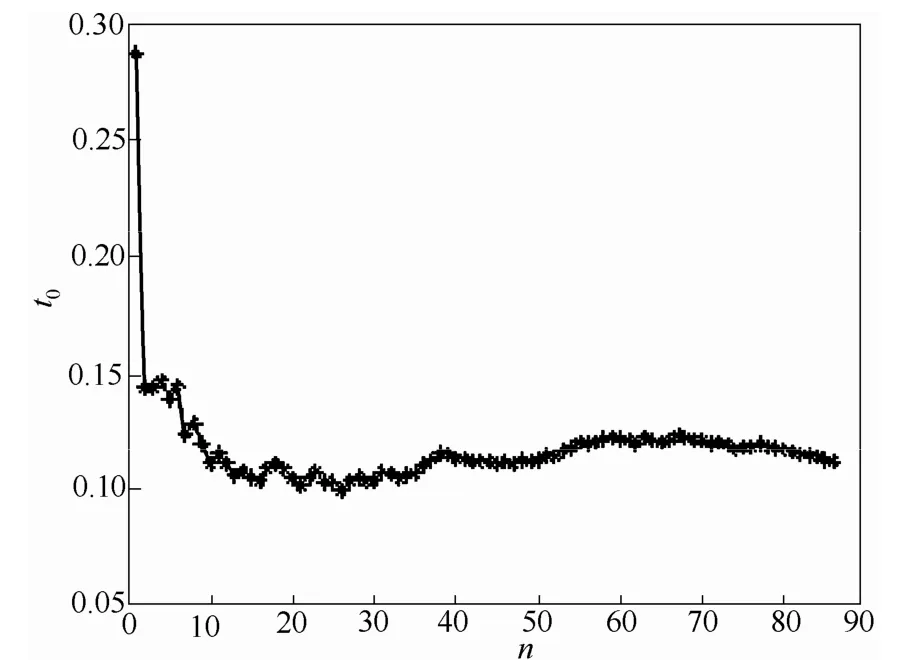
图3 H/L偏差概率Fig.3 H/L deviation probability

诊断行为属规则型，可用 HCR模式计算其失误概率EP2。

③ 操作员调节进料阀并开大冷回流，其失败概率EP3可用 THERP方法求出。

（2）建模与计算

① 根据化工行业基本情况及假定得，EP1=1.00×10-4。

② 根据专业人员及操作人员的经验，可得以下数据。

根据热工水力学计算[30]，操纵员需在CT1=14.6 min内完成调节进料阀并开大冷回流。根据化工企业基本情况及假设，操纵员经过平均水平训练（有6个月操作经验），操纵员在此工况下（潜在应急情景）有一定的心理压力，其修正因子取0.28。根据热工水力学计算，由事故发生到引发塔顶温度超高报警的时间CT2为3 min。根据化工企业基本情况及假设，操纵员执行 DEC规程（冲塔诊断）的时间CT3为4 min。由于操纵员进入A1规程后所采取的第1个行为就是根据蒸汽流量高信号作出降量并调节冷回流的诊断，操纵员在A1规程中的执行时间很短，可忽略。一回路操纵员完成调节进料阀的操作时间CT4为5 min，二回路操纵员完成加大冷回流的时间CT5为5 min。一回路操纵员与二回路操纵员同时进行各自的操作行为，所以事故处理中总操作时间1 min计算。

允许操作员进行诊断的时间

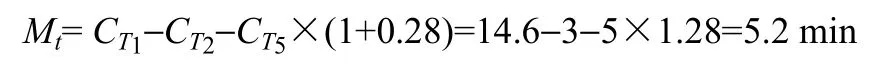
平均诊断时间CT1/2=CT3=4 min

（3）操纵员调节进料阀和开大冷回流，其HRA事件树如图4所示（不考虑纠错）。图中，a代表操纵员成功调节进料量；A代表操纵员未成功调节进料量；b代表操纵员成功调节冷回流；B代表操纵员未成功调节冷回流。

依据 THERP 手册分析得到

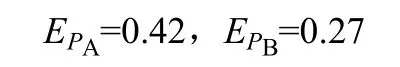
该事件树的成功概率为

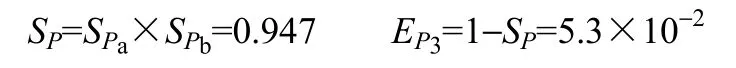
事件失误率

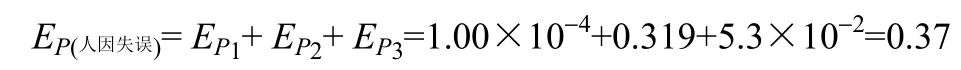
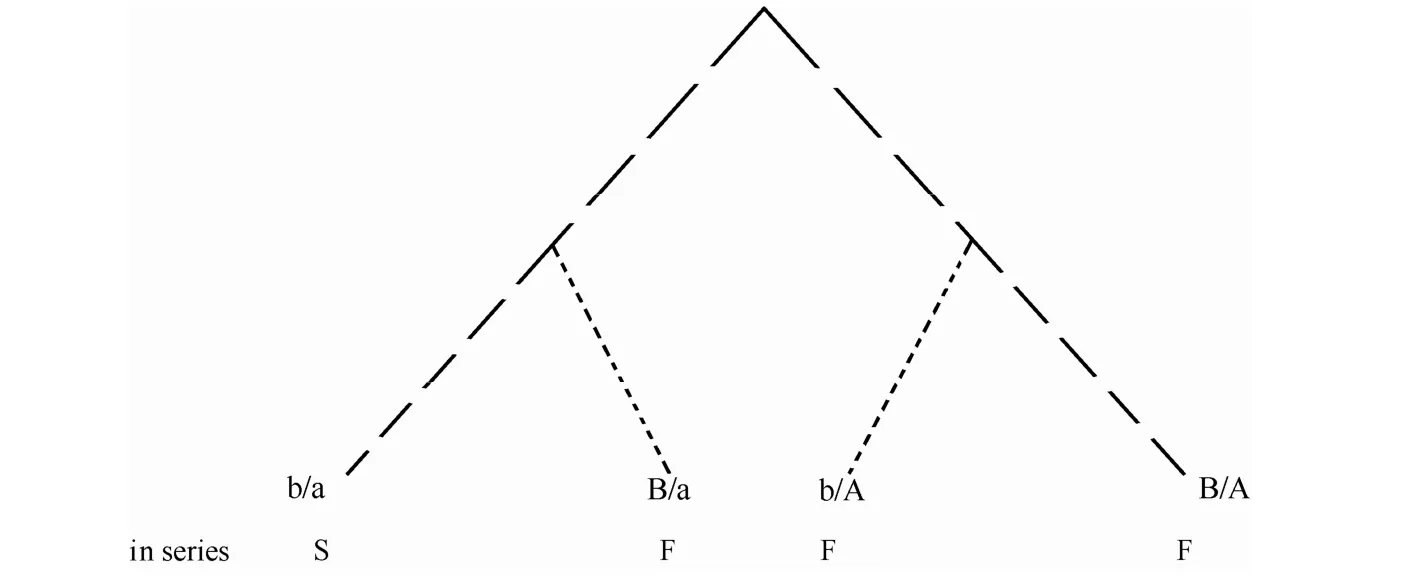
图4 HRA事件树Fig.4 HRA event tree

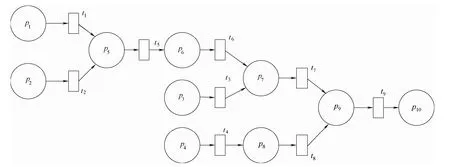
图5 分馏塔冲塔故障发生过程模糊Petri网模型Fig.5 Fuzzy Petri net model for occurrence of tower fault

3.2.3 大尺度工艺偏差概率估计 根据式（5），计算修正后的工艺偏差概率即为大尺度上的工艺偏差概率。

3.3 冲塔事故概率估计

以分馏塔冲塔事故发生过程中存在的工艺偏差为库所P，某一偏差发生的过程为变迁T，基于分馏塔冲塔事故的HAZOP分析构建分馏塔冲塔事故发生过程模糊Petri网模型如图5所示。这里库所可信度表示各工艺偏差的概率值，其值可由前面章节计算方法求得；变迁规则可信度表示各工艺偏差被触发的概率值，其值由10位专家经验给出，取平均值如表1所示。

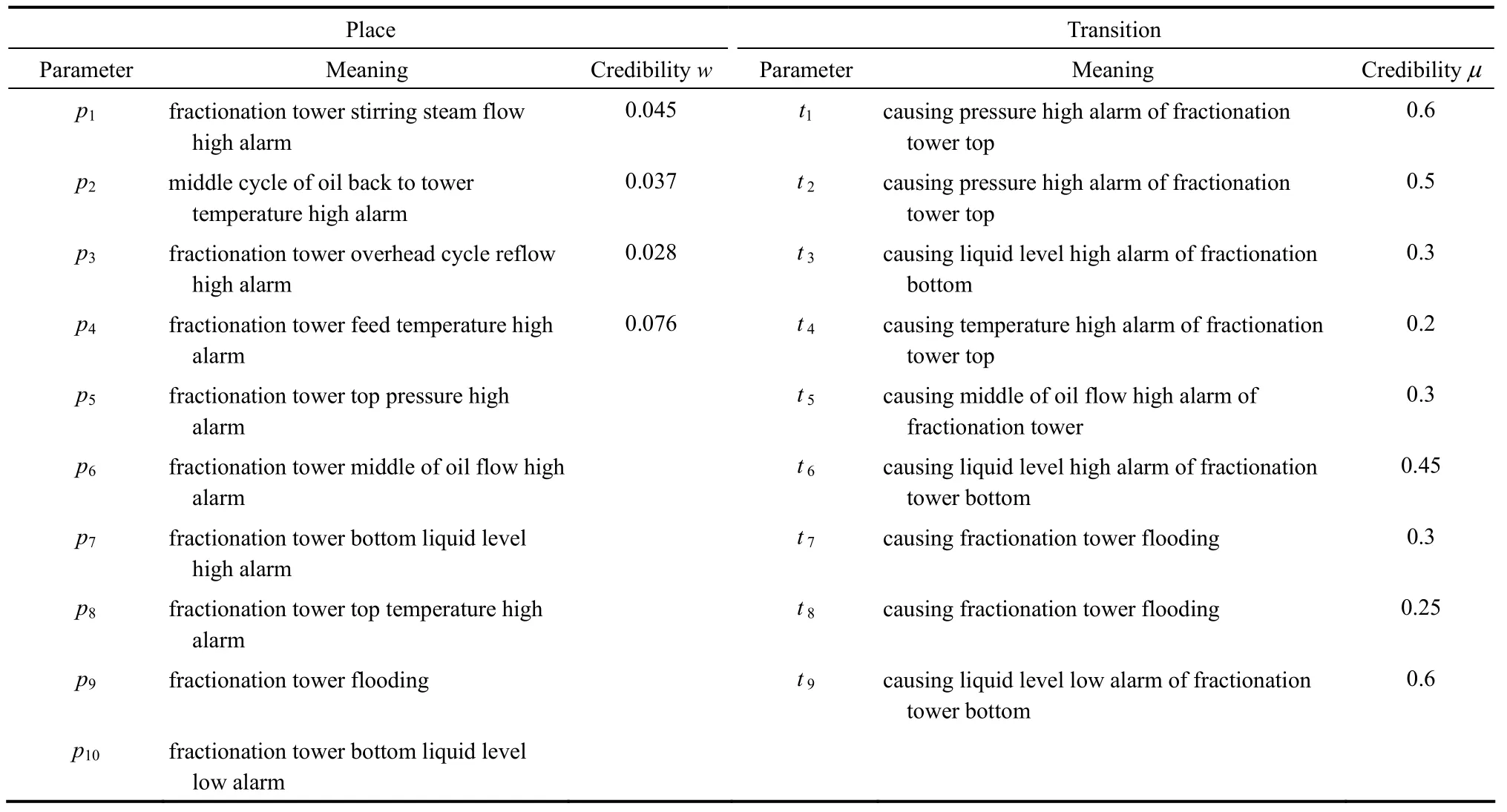
表1 分馏塔冲塔故障FPN模型中各参数含义及取值Table 1 Fractionation tower flooding FPN model of meaning and value of parameters

确定初始状态矩阵及变迁可信度集合

根据FPN的定义，可确定输入矩阵IN和输出矩阵OUT为

通过计算可得，为各库所的实际可信度集合，M(6)=[0.045,0.037,0.028,0.076,0.0455,0.0137,0.0145,0.0152,0.0082,0.0049]，即分馏塔顶压力高报警概率为0.0455，分馏塔中段油流量高报警概率为0.0137，分馏塔底液位高报警概率为0.0145，分馏塔顶温度高报警概率为0.0152，分馏塔冲塔故障概率为0.0082，分馏塔底液位低报警概率为0.0049。结果表明本文提出的事故概率估计方法与传统方法相比，具有以下优势。

（1）在基本事件的选取上，从工艺偏差角度分析，更符合过程安全的风险传播特点。

（2）工艺偏差概率估计数据来源于现场采集的报警监测数据，不同的现场数据不同且更新快，更符合特定现场工况。

（3）引入多尺度思想，考虑了不同尺度上的各种控制因素，如大尺度上考虑了人因失误，使所求结果更为合理可靠。

（4）本案例计算分馏塔冲塔故障概率为0.0082。通过本文分析可以减小人因失误概率来降低与之相关的参数偏差概率，从而降低冲塔事故概率，为企业过程安全的控制提供依据。

4 结 论

化工过程安全事故大多由于系统的“变化”引起，如液位偏高、流量过大等。传统的事故概率估计方法专注于机械设备损坏、人为破坏、偏差影响等，考虑因素较杂，并不能很好地适用于过程安全的风险评价。本文提出的事故概率估计方法，具有以下优势。

（1）引入了多尺度思想，提出了过程安全的尺度效应等有关定义，揭示化工过程风险因子的尺度效应及多尺度特征。本文在小尺度上只考虑工艺偏差概率为基本事件概率，大尺度上考虑人因失误对工艺偏差带来的影响并对其修正，所得基本事件的概率比查数据库所得数据更符合实际工况。

（2）提出了一种小尺度工艺偏差概率建模方法。对工艺偏差概率在小尺度上的表征方式进行研究。基本事件理解为工艺偏差H/L报警，仅着眼于工艺参数角度，不考虑任何机械问题，更符合过程安全的风险传播特点。

（3）提出了一种大尺度工艺偏差概率建模方法。对工艺偏差概率在大尺度上的表征方式进行研究，结合了人因失误理论，具有更好的实际意义。

当然也存在许多不足，在不同的尺度，可以考虑不同控制因素对工艺偏差的影响，如BPCS反馈作用、参量偏差间的相互影响等，这都是接下来要研究的方向。

符 号 说 明

CT1/2——在具体的事件中，用关键行为形成因子修正的CT1/2,nominal

CT1/2,nominal——在具体的事件中，所有被测得的工作人员辨识所用时间的中值

CT1——调节进料阀并开大冷回流允许时间

CT2——由事故发生到引发塔顶温度超高报警的时间

CT3——操纵员执行DEC规程（冲塔诊断）的允许时间

CT4——一回路操纵员完成调节进料阀的允许时间

CT5——二回路操纵员完成加大冷回流的允许时间

EP——行为失效概率

EPA——操纵员未成功调节进料量的概率

EPB——操纵员未成功调节冷回流的概率

EP(HCR)——HCR 分析阶段，可能的人员响应失误概率

EP(THERP)——THERP 分析阶段，具体的干预操作行为中可能的失误概率

EP1——操作员由塔搅拌蒸汽流量高报警进入 DEC规程即冲塔规程诊断阶段，可能的失误概率

EP2——操作员由冲塔规程诊断进入冲塔确认阶段即A1规程，作出的降量并调节冷回流的判断，用 HCR模式计算的可能的失误概率

EP3——操作员调节进料阀并开大冷回流，其可能的失误概率

EP(大尺度)——大尺度上，行为失效概率（用人因失误概率修正了工艺偏差概率所得）

EP(小尺度)——小尺度上，行为失效概率（实际上，只考虑了工艺偏差概率）

EP(修正)——人因失误概率

LT——统计时间段长度

Mt——操作员对突发事件反应时间的最大值

n——统计时间段个数

RTi——变量在第i个时间段内的总恢复时间

SP——行为成功概率

SPa——操纵员成功调节进料量的概率

SPb——操纵员成功调节冷回流

t0——工艺变量偏差概率

[1]周东华,李钢,李元.数据驱动的工业过程故障诊断技术——基于主元分析与偏最小二乘的方法[M].北京：科学出版社,2011：1-11.ZHOU D H,LI G,LI Y.Data-driven Industrial Process Fault Diagnosis Technology—Based on Principal Component Analysis and Partial Least Squares[M].Beijing：Science Press,2011：1-11.

[2]胡瑾秋,张来斌,王安琪.炼化装置故障链式效应定量安全预警方法[J].化工学报,2016,67(7)：3091-3100.HU J Q,ZHANG L B,WANG A Q.Quantitative safety early warning method of fault propagation for petrochemical plants[J].CIESC Journal,2016,67(7)：3091-3100.

[3]WU T K,WANG B,ZHAO Y,et al.Renovated fault analysis method for ammonia leakage based on the fault tree analysis[J].Journal of Safety and Environment,2014,14(4)：15-20.

[4]PAPAZOGLOU I A.Functional block diagrams and automated construction of event trees[J].Reliability Engineering and System Safety,1998,61(3)：185-214.

[5]张进春.重油催化裂化系统安全分析与关键风险评价研究[D].长沙：中南大学,2007.ZHANG J C.System safety analysis and critical risk assessment of heavy oil catalytic cracking[D].Changsha：Central South University,2007.

[6]XIAO R,YANG D.The research on dynamic risk assessment based on Hidden Markov Models[C]//Proceedings of the 2012 International Conference on Computer Science & Service System.Washington DC,2012：1106-1109.

[7]贾朋美,於孝春,宋前甫.Bow-tie技术在城镇燃气管道风险管理中的应用[J].工业安全与环保,2014,40(2)：14-18.JIA P M,YU X C,SONG Q F.Application of bow-tie technology in the risk management of urban gas pipeline[J].Industrial Safety and Environmental Protection,2014,40(2)：14-18.

[8]FLEMING K N.Markov models for evaluating risk-informed in-service inspection strategies for nuclear power plant piping systems[J].Reliability Engineering and System Safety,2004 ,83(1)：27-45.

[9]GRAN B A.Use of Bayesian belief networks when combining disparate sources of information in the safety assessment of software-based systems[J].International Journal of Systems Science,2002,33(6)：529-542.

[10]TOUW A E.Bayesian estimation of mixed Weibull distributions[J].Reliability Engineering and System Safety,2009,94(2)：463-473.

[11]CHENG L V,ZHANG Z Y,REN X.Predicting the frequency of abnormal events in chemical process with Bayesian theory and vine copula[J].Journal of Loss Prevention in the Process Industries,2014,9(4)：192-200.

[12]ADAMYA A,HE D.Failure and safety assessment of systems using Petri nets[C]//Robotics and Automation,2002.Proceedings.ICRA'02.IEEE International Conference on.IEEE,2002,2：1919-1924.

[13]VOLOVOI V.Modeling of system reliability Petri nets with aging tokens[J].Reliability Engineering and System Safety,2004,84(2)：149-161.

[14]YIN S Q,LIANG F Y,YAO X Q.Dynamic risk prediction for the deep excavations based on neutral networks and it’s applications[J].Chinese Journal of Underground Space and Engineering,2011,7(5)：996-1000,1012.

[15]李修华.多因素影响下的 Monte Carlo 进度风险分析模型[D].上海：同济大学,2007.LI X H.Monte Carlo risk analysis model under the influence of multiple factors[D].Shanghai：Tongji University,2007.

[16]王雪,喻刚,王佳冰.高速公路项目融资风险的动态灰色模糊评价[J].重庆建筑大学学报,2008,30(5)：81-85.WANG X,YU G,WANG J B.Dynamic fuzzy evaluation of expressway project financing risk[J].Journal of Chongqing Architecture University,2008,30 (5)：81-85.

[17]GUPTA J P.Application of DOW’s fire and explosion index hazard classification guide to process plants in the developing countries[J].Journal of Loss Prevention in the Process Industries,1997,10(1)：7-15.

[18]刘耀龙.多尺度自然灾害情景风险评估与区划——以浙江省温州市为例[D].上海：华东师范大学,2011.LIU Y L.Scenario risk assessment and division of multi - scale natural disasters—a case study of Wenzhou city in Zhejiang province[D].Shanghai：East China Normal University,2011.

[19]WAGENET R J.Scale issues in agroecological research chains[J].Nutrient Cycling in Agroecosystems,1998,50(1/2/3)：23-34.

[20]GAGE S H,ISARD S A ,COLUNGA-G M.Ecological scaling of aerobiological dispersal processes[J].Agricultural and Forest Meteorology ,1999 ,97(4) ：249-261.

[21]MANNAN M S,SACHDEVA S,CHEN H,et al.Trends and challenges in process safety[J].AIChE J.,2015,61(11)：3558-3569.

[22]刘耀龙,牛冲槐,王军,等.论灾害风险研究中的空间尺度耦合[J].防灾科技学院学报,2012,14(3)：24-27.LIU Y L,NIU C H,WANG J,et al.Study on spatial scale coupling in disaster risk research[J].Journal of Disaster Prevention Science and Technology,2012,14(3)：24-27.

[23]臧灏,李宏光,杨帆,等.流程工业报警系统传统评估方法分析及改进[J].化工学报,2014,65(11)：4459-4464.ZANG H,LI H G,YANG F,et al.Analysis and improvement of process industrial alarm systems traditional assessment methods[J].CIESC Journal,2014,65(11)：4459-4464.

[24]SWAIN A D,GUTTMANN H E.Handbook of human-reliability analysis with emphasis on nuclear power plant applications[S].1983,NUREG/CR-1278.

[25]ZIMOLONG B.Empirical evaluation of THERP,SLIM and ranking to estimate HEPs[J].Reliability Engineering & System Safety,1992,35(1)：1-11.

[26]王洪德,高玮.基于人的认知可靠性(HCR)模型的人因操作失误研究[J].中国安全科学学报,2006,16(7)：51-56.WANG H D,GAO W.Study on erroneous operation due to human factor based on human cognitive reliability (HCR) model[J].China Safety Science Journal,2006,16(7)：51-56.

[27]宋洪涛.考虑组织管理因素整体影响的人因可靠性分析方法研究[D].衡阳：南华大学,2008.SONG H T.Study on human reliability analysis method considering the overall influence of organizational management factors[D].Hengyang：University of South China,2008.

[28]VALETTE R,CARDOSO J,DUBOIS D.Monitoring manufacturing systems by means of Petri nets with imprecise markings[C]// IEEE International Symposium on Intelligent Control.1989：233-238.

[29]郑远扬,郝富军.催化裂化分馏塔动态仿真数学模型和算法[J].化工学报,1994,45(6)：704-711.ZHENG Y Y,HAO F J.Mathematical model and algorithm for dynamic simulation of fractionating tower of catalytic cracking[J].Journal of Chemical Industry and Engineering(China),1994,45(6)：704-711.

[30]郑陆松,赵颍杰,孙宝芝,等.蒸汽发生器降负荷过程热工水力特性瞬态数值分析[J].化工学报,2015,66(S2)：116-122.ZHENG L S,ZHAO Y J,SUN B Z,et al.Transient numerical analysis of thermal and hydraulic characteristics of steam generator during load shedding process[J].CIESC Journal,2015,66(S2)：116-122.

date:2017-06-04.

GUO Jiajie,guo_jiajie@126.com

supported by the National Natural Science Foundation of China (51574263),the China University of Petroleum (Beijing) Research Fund (2462015YQ0403) and the China University of Petroleum (Beijing)Youth Innovation Team C project (C201602).

Accident probability estimation of process safety based on scale effect

HU Jinqiu,GUO Jiajie
(State Key Laboratory of Oil and Gas Resources and Engineering,College of Mechanical and Transportation Engineering,China University of Petroleum,Beijing102249,China)

In order to improve the applicability of probabilistic estimation methods for process safety accidents,the propagation process of deviations should be considered in the basic event stage.A method for estimating the probability of process safety accidents based on scale effects is proposed.A new basic event solving model is established from the point of view of process deviations.Multi-scale ideas are introduced to modify the basic event probability,on the large scale,by considering the effects of human errors on process deviations.The fuzzy Petri net model is used to estimate the accident probability.Finally,the model is analyzed and verified by the case analysis of the fractionating tower accident.The results show that the participation of human has a great influence on the probability of process deviations.The proposed method is more suitable for the practical conditions and process safety.Since the probability estimate is based on the statistical data,the deviation probability is calculated and the subjectivity of the calculation parameters is avoided.

multi-scale; process systems; accident probability; process deviation; human error; safety

X 937

A

0438—1157（2017）12—4848—09

10.11949/j.issn.0438-1157.20170716

2017-06-04收到初稿，2017-09-12收到修改稿。

联系人：郭家洁。

胡瑾秋（1983—），女，教授。

国家自然科学基金项目（51574263）；中国石油大学（北京）科研基金资助项目(2462015YQ0403)；中国石油大学（北京）青年创新团队C计划项目 (C201602)。