考虑氢气实际气体效应和阻塞流效应的螺旋槽干气密封动态特性分析

许恒杰，宋鹏云，毛文元，邓强国

（1昆明理工大学化学工程学院，云南 昆明 650500；2昆明理工大学环境科学与工程学院，云南 昆明 650500）

考虑氢气实际气体效应和阻塞流效应的螺旋槽干气密封动态特性分析

许恒杰1,2，宋鹏云1，毛文元1，邓强国1

（1昆明理工大学化学工程学院，云南 昆明 650500；2昆明理工大学环境科学与工程学院，云南 昆明 650500）

以 Chen等提出的氢气实际气体状态方程描述氢气的实际气体行为，以气体出口速度达到音速作为产生阻塞效应的条件，确定出口压力边界条件，采用小扰动法分析了干气密封操作参数对螺旋槽干气密封动态特性的影响规律，并与理想气体、强制出口压力边界模型中的动态特性系数进行了对比。结果表明：研究高压螺旋槽干气密封的动态特性时应当考虑实际气体效应和阻塞流效应。两种效应使氢气螺旋槽干气密封的直接动态气膜刚度减小，使直接动态气膜阻尼增大。随着压缩数、进口压力的增大，两种效应对动态气膜刚度的影响逐渐增强。以频率比为变量时，两种效应主要影响气膜刚度，对气膜阻尼的影响作用较小。针对所研究的工况，与理想气体和强制压力出口边界条件相比，考虑实际气体效应和阻塞流效应，以压缩数为变量时，动态气膜阻尼（Czz、Cαα、Cαβ）的平均偏差分别为2.28%、1.93%、2.79%；以进口压力为变量时，3种气膜阻尼的平均偏差分别达到4.08%、2.07%、1.82%。

螺旋槽干气密封；动态特性；实际气体；阻塞流；数值分析

引 言

在石油炼制、石油化工和煤化工行业中，加氢装置中的氢气压缩机是一种关键设备，而泵入式螺旋槽干气密封是氢气压缩机里应用较多的一种干气密封[1]，靠近介质侧干气密封的冲洗润滑介质一般为氢气。泵入式螺旋槽干气密封的高压侧位于密封端面外径处，低压侧位于密封端面内径处，一般与缓冲气体或大气相通。在径向方向上，由于密封间隙进出口之间的压差作用，润滑气体在端面外径处被泵入密封间隙，在内径处流出密封间隙。此过程中气体的流通面积是逐渐减小的，且润滑气体在密封坝区的流动是一个降压过程，从质量守恒和能量守恒两种角度出发，润滑气体在密封间隙内流动时速度会逐渐增大，一旦此速度达到音速，会使密封端面出口发生阻塞，导致出口压力大于环境压力，改变密封端面气膜压力分布规律[2]，从而会对泵入式螺旋槽干气密封性能产生一定的影响。

目前在干气密封性能的研究中，大多数学者均将气体的出口压力视为环境压力[3-5]（称为强制出口压力边界），考虑阻塞流效应的干气密封性能研究较少。1971年，针对光滑平面的泵出式端面密封，Zuk等[6]给出了密封发生阻塞时的出口压力解析表达式，在进口压力一定的前提下分析了进出口压比对气体泄漏率的影响，同时通过实验验证了其理论分析的正确性。Arghir等[7]对环形密封中的阻塞流提出一种数值计算方法，研究了存在阻塞流时环形密封的静态稳定性，指出若在出口处发生阻塞，环形密封可能发生失稳。Thomas等[8]认为气体在密封间隙出口发生阻塞时端面泄漏将达到最大，并将这一条件作为阻塞压力出口条件对端面光滑的锥形干气密封进行了热弹流润滑分析。马春红等[9]求解雷诺方程时将Zuk阻塞压力表达作为出口边界条件，研究了高速螺旋槽干气密封的稳态性能。同样，Thatte等[10]采用Zuk阻塞压力边界研究了螺旋槽干气密封坝区的Mach数和压力分布规律。以上研究报道均是针对阻塞流效应对干气密封稳态特性的影响。而工程应用已表明，干气密封气膜的动态特性不良是密封丧失稳定性的原因之一[11]，表征气膜动特性的两个系数（动态气膜刚度、阻尼）反映了气膜的动态稳定性能[12]。因此，开展干气密封气膜动态特性的研究对设计、评价干气密封的动态稳定性能具有重要意义。干气密封的动态性能分析是在其稳态性能的基础上展开的，发生阻塞流效应后，其动态特性必然会与亚音速流动的情况存在差异。迄今为止，尚未发现考虑出口阻塞流影响的干气密封动态特性研究，而开展干气密封动态特性研究是干气密封稳定性研究至关重要的部分。此外，大多数研究没有考虑润滑气体的实际气体行为，根据已有报道[13-14]，实际气体效应对干气密封的动态特性存在着一定的影响。综合考虑，忽略实际气体效应和阻塞流效应会影响干气密封性能的准确分析与评价。

本文以氢气为例，采用不同的实际气体状态方程计算氢气压缩因子，对密封出口速度进行判定，建立了考虑实际气体效应和阻塞流效应的泵入式螺旋槽干气密封动态特性分析数学模型，并通过算例验证了所建模型的正确性，研究了两种效应对螺旋槽干气密封动态特性的影响，并与理想气体、强制出口压力边界算例进行了对比，为螺旋槽干气密封的工程设计提供一定的理论依据。

1 几何模型

泵入式螺旋槽干气密封动态特性的分析模型如图1所示，动环端面外侧周向均匀开有12个螺旋槽，润滑气体被泵入密封间隙后，由于槽结构的特殊性和一定的转速，在槽根处会因压缩产生气体动压使干气密封动静环之间形成一定厚度的气膜，最后经由密封间隙内径流出。

2 数学模型

2.1 压缩因子

压缩因子Z实质上表示实际气体比容Vre与相同温度、相同压力下理想气体比容Vid之比，按理想气体状态方程的形式pVid=RT，实际气体状态方程可以写成

明显地，当Z=1时，式(1) 为理想气体状态方程；Z＜1时，可认为是同温同压下，实际气体的比容小于理想气体的比容，即实际气体更易于压缩；当Z＞1时情况则恰好相反。

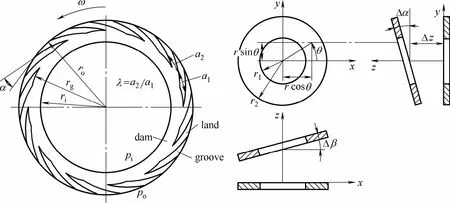
图1 螺旋槽干气密封动态特性分析模型[15]Fig.1 Dynamic analysis model of spiral groove dry gas seal[15]

建立一个既适用于所有气体，而且压力、温度又包括宽广的范围、同时能确切反映实际气体行为的通用方程是很困难的。因此，实际气体的压缩因子需要根据气体的种类选用合理的状态方程进行计算。目前，计算压缩因子的手段有多种，主要包括Redlich-Kwong（R-K）方程、维里（Virial）方程和拟合NIST数据等，维里方程为二阶项维里方程，Chen等[16]通过对NIST数据进行拟合，在温度为173～393 K、压力为0.1～100 MPa范围内，得出了一个氢气的实际气体状态方程。

以氢气为例，采用以上3种方式计算的压缩因子Z随压力的变化趋势如图2所示。可以看出，随着压力的增大，R-K方程、Chen等提出的氢气状态方程与NIST数据均保持良好的吻合性，相对于其他两种方程，二阶项维里方程与NIST数据之间的偏差略大。为了确定精确的氢气压缩因子表达方式，计算3种压缩因子方程与NIST数据之间的平均误差分别为0.272%、0.263%、1.985%。因此，本文选用Chen等提出的氢气状态方程表达氢气的实际行为。

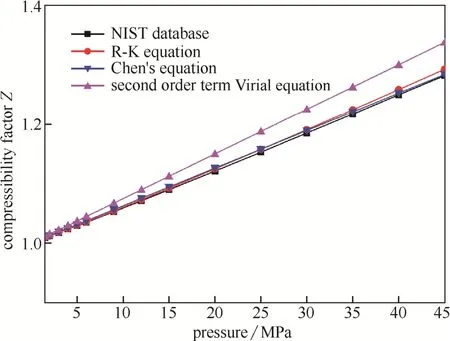
图2 压缩因子随压力变化的趋势（T=303.15 K）Fig.2 Compressibility factor versus pressure (T=303.15 K)

Chen的氢气状态方程中的压缩因子为

式中，B为常数，其值为1.9155×10-6K·Pa-1。

2.2 实际气体的音速

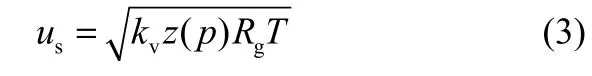
式中，kv=Z/(Z-RZT2/cp)为实际气体的容积绝热指数，其中ZT为导数压缩因子，cp为实际气体的比定压热容。可以看出，当气体为理想气体时，kv等于理想气体的比热比γ，式（3）可以化为理想气体的音速公式c=(γRgT)0.5。导数压缩因子ZT的计算如下[18]

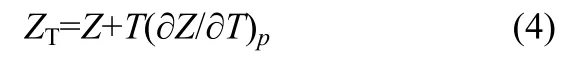
实际气体比定压热容cp的计算按文献[19]的方法进行。

2.3 压力控制方程

螺旋槽干气密封的端面气膜厚度一般为微米级，与端面气膜的径向和周向尺度相比，其轴向方向上的压力梯度可以忽略不计，则密封端面间的气膜压力选用二维柱坐标下可压缩流体的雷诺方程进行描述

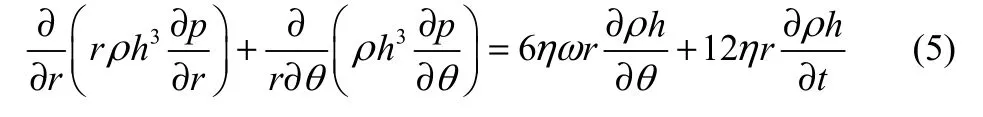
式中，η为润滑气体的黏度；ρ为润滑气体的密度，ω为干气密封的转速。

文献[9]对绝热流动和等温流动两种假设下螺旋槽干气密封发生阻塞时的质量流量进行了计算，发现等温流动假设下其理论计算结果更接近Zuk的实验结果。本文假设密封端面间的气体流动为等温流动，润滑气体为牛顿流体。

联立式（1）和式（3）并代入式（5）中即可得考虑实际气体效应的螺旋槽干气密封压力控制方程。在干气密封的实际运行过程中，旋转动环往往会发生轴向微振和角向偏摆，气膜厚度在轴向和角向方向上会产生微小的波动。因此，将干气密封受到外部激励ω1而发生的微小运动视为在平衡运动状态上的叠加，采用小扰动法可推导出考虑实际气体效应的量纲1稳态、动态雷诺方程，具体的推导过程可参考文献[13,15,20]。

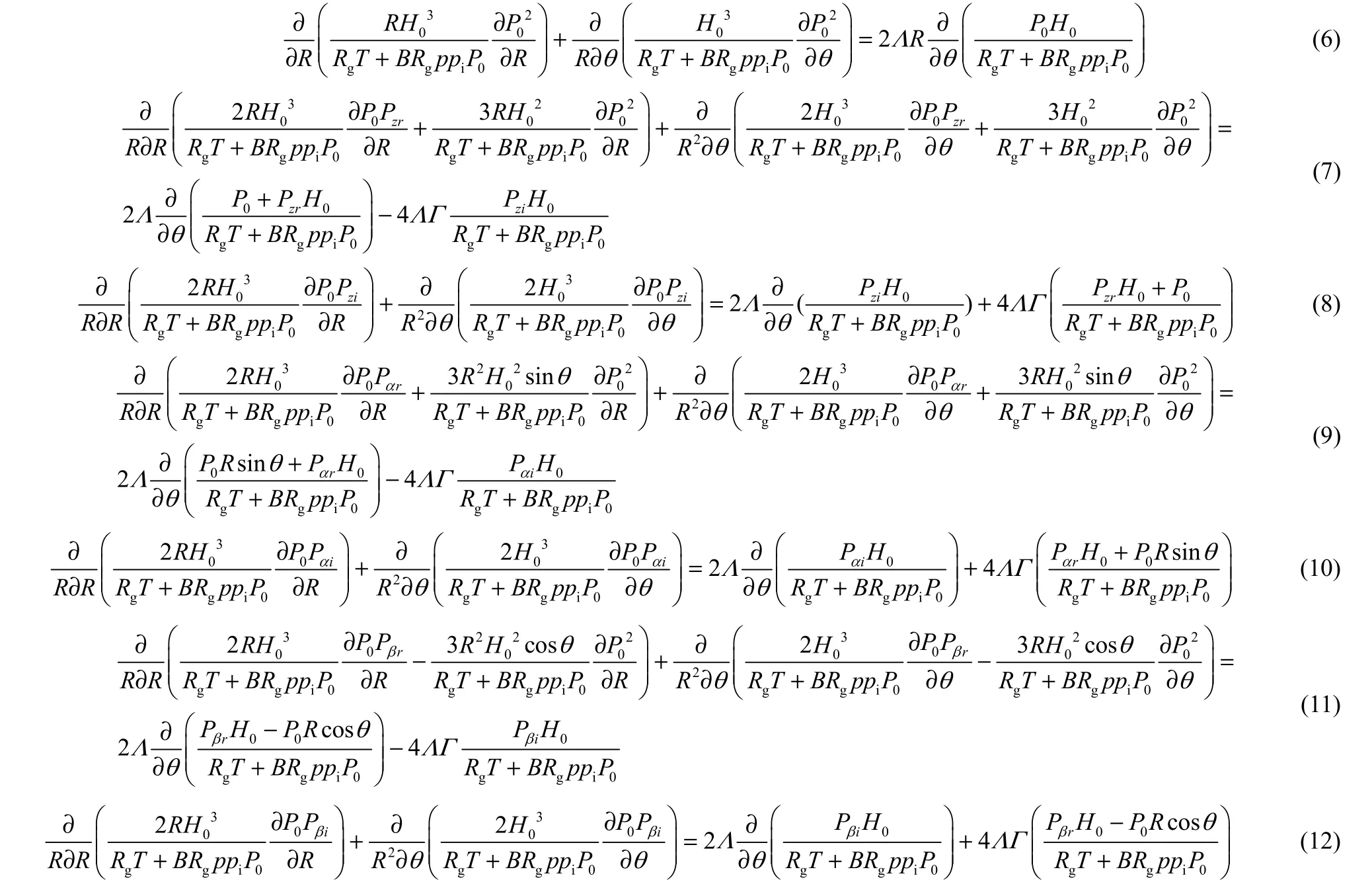
式中，量纲1变量定义如下

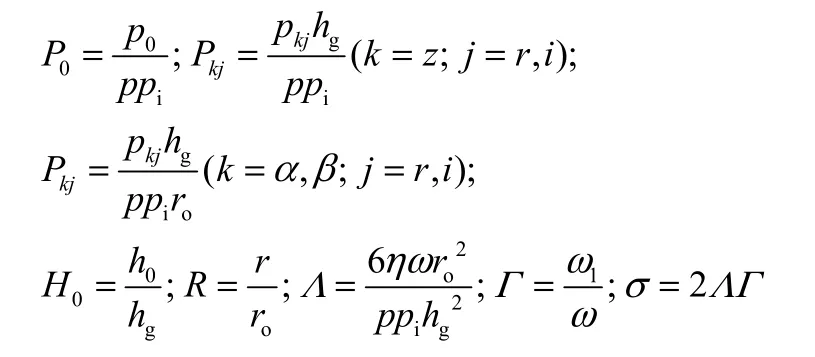
其中，p0为稳态压力，ppi为参考压力，文中取为5 MPa，hg为槽深，h0为平衡膜厚，ro为密封环外径，Λ为压缩数，Γ为频率比，σ为频率数，pzr、pzi为轴向微扰压力。在图1中，定义α向为动环绕x轴偏摆的方向，则pαr、pαi为使动环绕x轴偏摆的角向微扰压力，β向为动环绕y轴偏摆的方向，则pβr、pβi为使动环绕y轴偏摆的角向微扰压力。

2.4 定义端面气膜动态特性系数

如图1所示，密封环受3个自由度的微扰，动态特性参数有18个。已有的三自由度微扰下干气密封动态特性研究表明[21]，干气密封受三自由度微扰的运动可以简化为两种相互独立的微扰运动，即轴向的微扰运动和沿两个正交轴作角向摆动的微扰运动，因此轴向微扰引起的角向动特性系数或角向微扰引起的轴向动特性系数可以忽略不计。同时，由于端面气膜的轴对称性，α向和β向微扰引起的动态特性系数满足以下关系：Kαα=Kββ、Kαβ=-Kβα、Cαα=Cββ、Cαβ=-Cβα。这里将由j向微扰引起的j向动态刚度、阻尼称为直接动态刚度、阻尼，其余的称为交叉耦合动态刚度、阻尼，其中j=α、β。即干扰自身方向的动态刚度和阻尼称为直接动态刚度、直接动态阻尼；干扰引起的另外两个方向的刚度和阻尼，称为交叉耦合刚度和交叉耦合阻尼。因此，本文具体以轴向直接动态刚度、阻尼系数（Kzz、Czz），角向直接动态刚度、阻尼系数（Kαα、Cαα），角向交叉耦合动态刚度、阻尼系数（Kαβ、Cαβ）为研究对象，其余12个动特性系数不予以讨论。定义端面

气膜动态刚度和动态阻尼系数计算式如下[22]

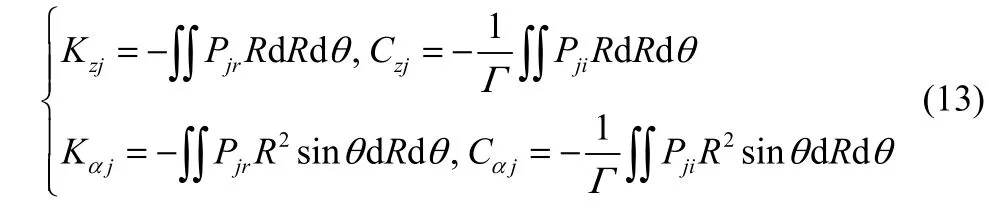
因此，有量纲动态特性系数与量纲1动态特性系数之间的关系可根据量纲1变量的定义导出

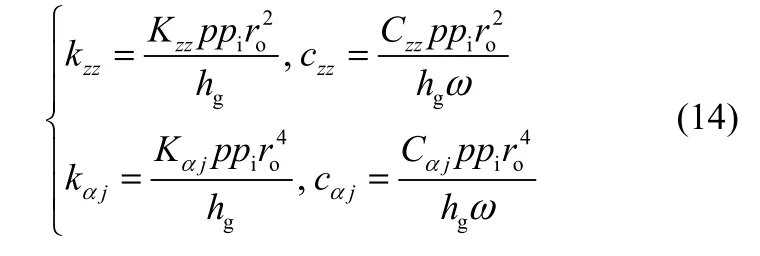
动态刚度反映了受到微扰时气膜抵抗变形的能力，其包含稳态气膜刚度；动态阻尼反映了受到微扰时气膜抑制振动发散的能力，即阻尼越大，气膜越易趋于稳定。

3 数值求解

3.1 计算方法

采用向后和中心差分，可以将式（6）～式（12）离散，具体的差分离散格式可以参考文献[23]。考虑到密封间隙出口处可能会发生阻塞，在迭代计算过程中需对气体的出口速度进行判定，从而选用合适的出口压力边界。由于在端面气膜密封中，对于密封坝区的气体泄漏通常采用经典的黏性可压流理论(即与膜厚3次方的关系)来分析，且文献[15]已指出径向泄漏率主要由压差流引起，转速引起的剪切流对径向泄漏率的影响不大，即旋转效应对径向速度和径向泄漏率的影响可以忽略，因此上述的出口速度指的是润滑气体的径向速度。值得注意的是，这里仅是指气膜厚度确定后，计算泄漏率和出口速度时不考虑旋转速度的影响。实际上，旋转速度对端面气膜厚度，即密封间隙的形成有重要贡献，在计算气膜厚度时考虑了转速的影响。此外，在目前干气密封端面间隙出口处考虑阻塞流效应的研究文献中，都有考虑入口压力损失，但是通过分析文献[9]中的数据发现，针对泵入式螺旋槽干气密封，考虑入口损失后的进口压力与原进口压力仅仅相差 1%左右，因此为了简化计算，本文忽略入口压力损失。

在稳态压力的迭代计算过程中，首先对出口压力边界赋一初值（出口处环境压力），迭代计算后获得出口速度uexit，然后与此出口压力下的实际气体音速us进行比较，若uexit小于或等于us，则以此出口压力作为出口的压力边界条件进行后续计算；若uexit大于us，则需对出口压力边界重新赋值，直至uexit等于us为止[24]后才进行稳态、动态压力迭代计算。以轴向动态刚度与阻尼为例，具体的计算流程如图3所示，角向动态刚度与阻尼的计算过程与之类似。

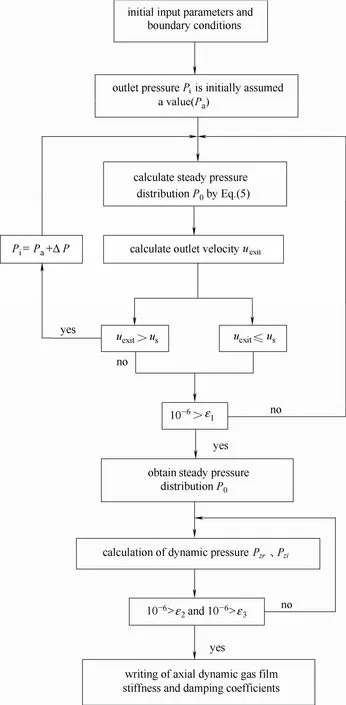
图3 计算流程Fig.3 Calculation procedure

3.2 边界条件

在迭代计算稳态、动态气膜压力时，需要给定边界条件，在迭代中边界条件分为两类。

（1）在密封环的外、内侧，即润滑气体进、出口处，轴向、角向微扰压力和稳态进口压力分别满足[25]Pjr=0，Pji=0，Po=po/ppi

（2）周期性边界条件

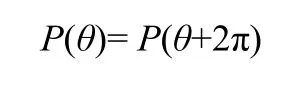
这里P为量纲1稳态压力、微扰压力的统称，包含P0、Pjr、Pji，其中j=z、α、β。

4 算例验证

4.1 出口阻塞流算法验证

在密封环内、外径分别为70 mm和90 mm，进口压力为 20 MPa，密封间隙为 3.17 μm，转速为261.8 rad·s-1的工况下，计算了光滑平行端面干气密封的压力分布，并与文献[8]的数据进行了对比，对比结果如图4所示。可以看出本文算法所得的结果与Thomas等[8]的计算结果趋势一致，出口压力约相差4%。说明本文的出口阻塞流算法是合理的。

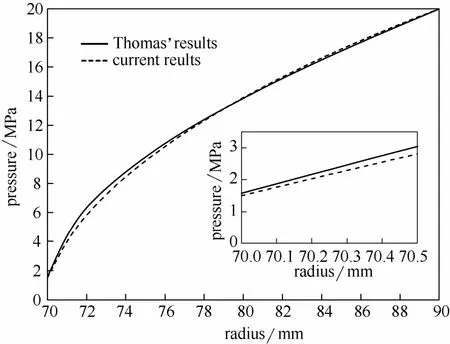
图4 阻塞出口边界压力计算值与文献值对比Fig.4 Comparison of steady pressure distribution between current study and Thomas’ at choked boundary

4.2 密封动态特性算法验证

在润滑气体为理想气体、密封间隙进出口均采用强制压力出口边界的前提下，Ruan[26]采用有限元法给出了三自由度微扰下螺旋槽干气密封的动态刚度和阻尼数据。本节选用 Ruan的计算参数，将压缩因子取为 1，即B=0，同时不对密封间隙的出口速度进行判定，选定大气压力作为干气密封出口压力，选取轴向动态气膜刚度和阻尼作为验证参数，对本文的动态特性算法进行验证。

案例计算参数：密封环内径ri=30 mm；外径ro=42 mm；螺旋槽槽根半径rg=33.6 mm；螺旋角α=20°；槽深hg=5 μm；槽台比为 1；气体黏度η=1.79×10-5Pa·s；大气压力pa=0.101 MPa；进口压力po=0.303 MPa。

将计算值转化成有量纲的刚度与阻尼，本文算法所计算的螺旋槽干气密封轴向动态气膜刚度和阻尼系数与文献值的对比如图5所示，可以看出，随着频率比Γ的增大，本文的刚度系数和阻尼系数计算结果与文献值趋势一致，数值相差不大，这说明本文的差分格式、网格密度、迭代精度控制都是合理的，轴向动态刚度系数和阻尼系数的计算程序是有效的。

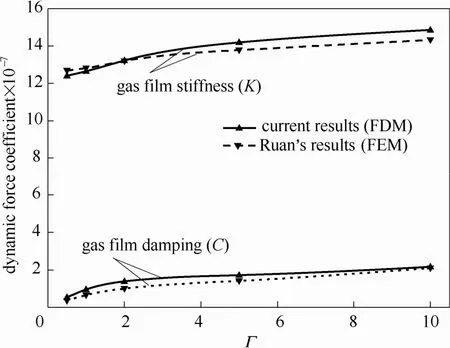
图5 动态特性系数计算值与文献值对比Fig.5 Comparison of dynamic force coefficients between current study and Ruan’s

5 结果分析与讨论

在此节中，螺旋槽干气密封的槽深hg=3 μm，平衡膜厚h0=3 μm，其余的结构参数沿用4.2节中的数据。由于螺旋槽干气密封的动特性系数随其结构参数的变化规律已有了充分的研究[27-29]，因此本文侧重于密封操作参数，选取压缩数Λ、频率比Γ和进口压力po作为变量（其中压缩数可反映干气密封的转速），探讨实际气体效应和阻塞流效应对螺旋槽干气密封动特性系数的影响。润滑气体选用氢气，其温度为 298.15 K，黏度为η=8.9135×10-6Pa·s，气体常数R=8.314 J·(mol·K)-1。需要说明的是，文中的算法是经过量纲1化的，因此若没有特别说明，后续分析中的参数均为量纲1值。

此外，定义了4种计算模型：考虑实际气体效应和阻塞流效应模型（CaseⅠ）；实际气体和强制压力出口边界模型（Case Ⅱ）；理想气体和阻塞压力出口边界模型（Case Ⅲ）；理想气体和强制压力出口边界模型（Case Ⅳ）。

5.1 压缩数Λ的影响

选定频率数σ=20，进口压力为20 MPa。考虑实际气体效应、阻塞流效应和理想气体、强制压力出口边界两种模型中的动态刚度随压缩数的变化，结果如图6所示。从压缩数的定义可以得知，当其他参数保持不变，压缩数可以表征干气密封的转速大小。从图6可以看出，就绝对值而言，在两种模型中，轴向、角向直接动态刚度（Kzz、Kαα）、角向交叉耦合动态刚度Kαβ均随压缩数的增大而近似呈线性增长。可以认为这是由较高的转速导致密封端面间出现了较强的动压效应，从而使得密封端面间压力增大所致。对比两种模型中的动态刚度计算结果，可以发现考虑实际气体效应和阻塞流效应时的动态刚度小于理想气体、强制压力出口边界时的动态刚度，动态刚度在两种模型之间的偏离程度随压缩数的增大而逐渐变得显著，在所研究的压缩数范围内，3种动态刚度在两种模型之间的平均误差分别约为 9.17%、11.6%和 0.958%，最大偏差分别为9.52%、16.8%、1.99%。

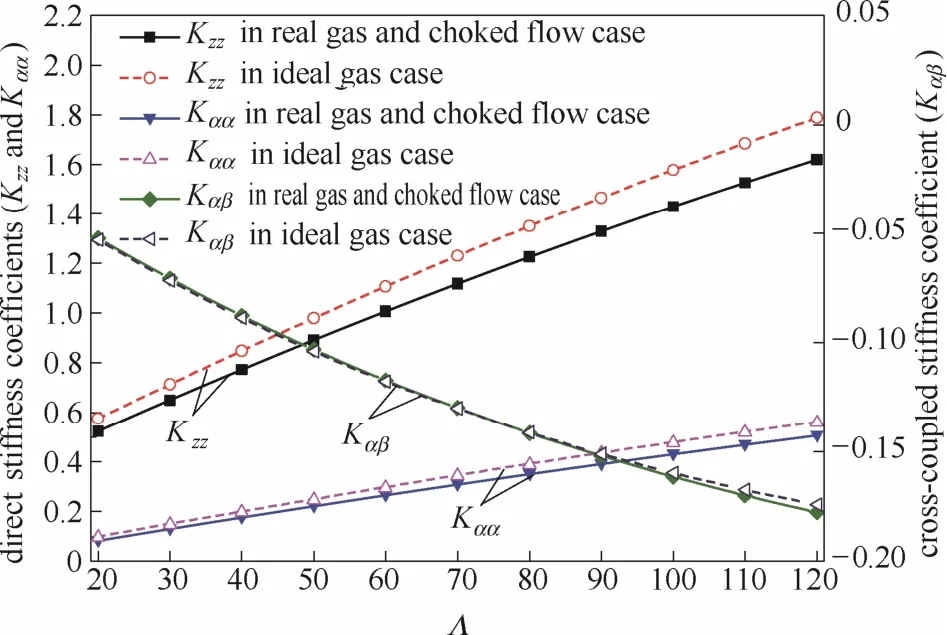
图6 压缩数对动态刚度的影响Fig.6 Dynamic stiffness coefficients change with squeeze number

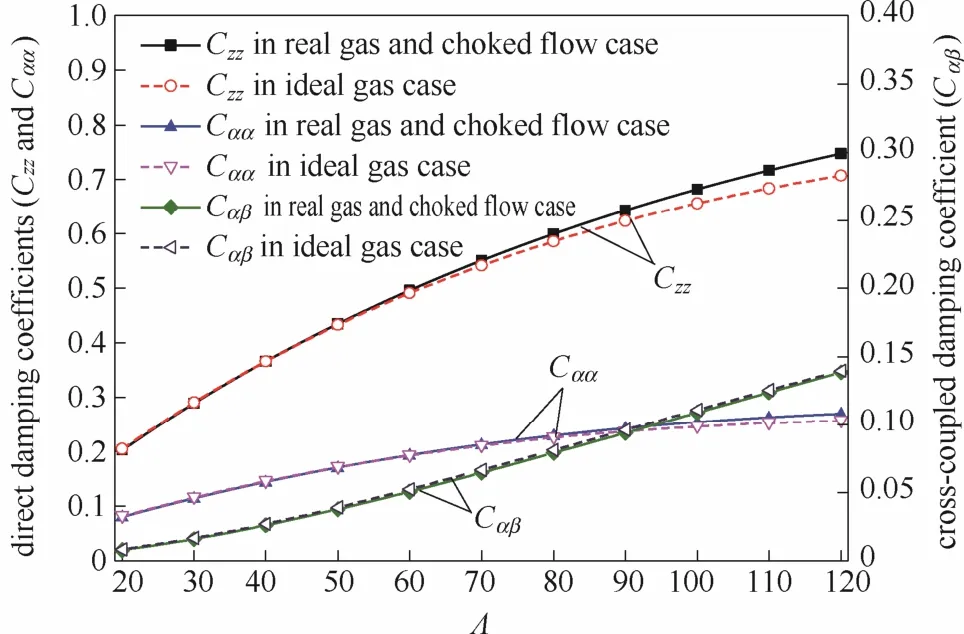
图7 压缩数对动态阻尼的影响Fig.7 Dynamic damping coefficients change with squeeze number

压缩数对动态阻尼系数的影响如图7所示，两种模型中的量纲1动态阻尼系数随着压缩数的增大而增大，这与文献[15]中螺旋槽顺流泵端面气膜密封阻尼系数随压缩数的变化规律相似，但是有量纲直接动态阻尼系数的变化趋势恰好与之相反，具体数据如表1所示。压缩数增大，有量纲直接动态阻尼减小意味着高转速下气膜的稳定性变差。同时从表1可以看出，有量纲直接动态阻尼系数czz的值要远远大于cαα的值，这说明高转速工况下密封容易失稳，且相较于轴向运动，随着转速的增大端面气膜密封的角向运动更容易发生失稳。这些状况与端面气膜密封稳定性分析和实践运行的结果吻合。另外，CaseⅠ中的动态阻尼大于 Case Ⅳ中的动态阻尼。两种模型之间的平均动态阻尼偏差分别为2.28%、1.93%和2.79%，最大偏差分别为5.77%、5%、3.91%。

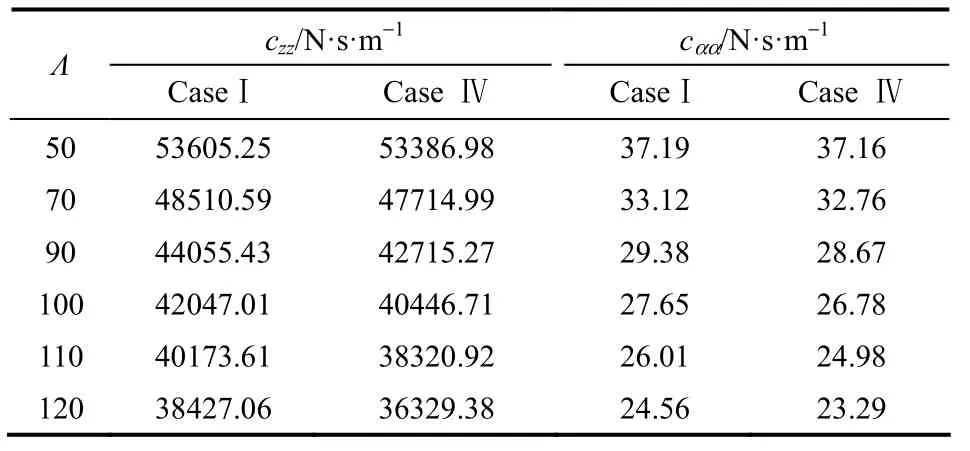
表1 有量纲直接动态气膜阻尼随压缩数的变化Table 1 Dimension direct dynamic damping coefficients change with squeeze number

实际气体效应和阻塞流效应分别对干气密封气膜的动态特性系数产生何种具体的影响很难从图6和图7看出。因此，以轴向直接动态刚度和阻尼（均为有量纲值）作为分析对象，比较了4种计算模型中的气膜动特性系数，如图8所示。根据前述对4种计算模型的定义，CaseⅠ和CaseⅢ、CaseⅡ和 CaseⅣ中动态特性参数之间的差异表示实际气体效应对干气密封动特性的影响；CaseⅠ和 CaseⅡ、CaseⅢ和CaseⅣ中的动态特性参数之间的差异表示阻塞流效应对干气密封动特性的影响。可以看出，4种模型中计算所得的气膜轴向直接动态刚度满足以下关系：CaseⅠ＜Case Ⅲ、CaseⅡ＜Case Ⅳ；CaseⅠ＜ CaseⅡ、Case Ⅲ＜Case Ⅳ，这说明当润滑气体为氢气时，不管密封出口是否发生阻塞，实际气体效应均使动态气膜刚度减小；不管润滑气体被视为实际气体还是理想气体，阻塞流效应同样使动态气膜刚度减小。而气膜轴向直接动态阻尼则满足：CaseⅠ＞ Case Ⅲ、CaseⅡ＞Case Ⅳ；CaseⅠ＞CaseⅡ、Case Ⅲ＞Case Ⅳ，这说明实际气体效应和阻塞流效应均使动态气膜阻尼增大。对于两种效应使动态刚度减小、使动态阻尼增大这一现象，这是由于氢气的压缩因子大于 1，较理想气体而言，氢气实际气体具有更大的比体积；再者阻塞流效应会提升密封间隙的出口压力，导致干气密封进出口压差减小。在气膜厚度一定的情况下，两种效应均使得密封的泄漏率减小，此时相较于理想气体，氢气实际气体密度较小，气膜吸收外界干扰能量的能力增强，抑制振动发散的能力提高，因此将润滑气体视为理想气体和考虑阻塞流效应时，气膜具有较小的动态刚度和较大的动态阻尼。

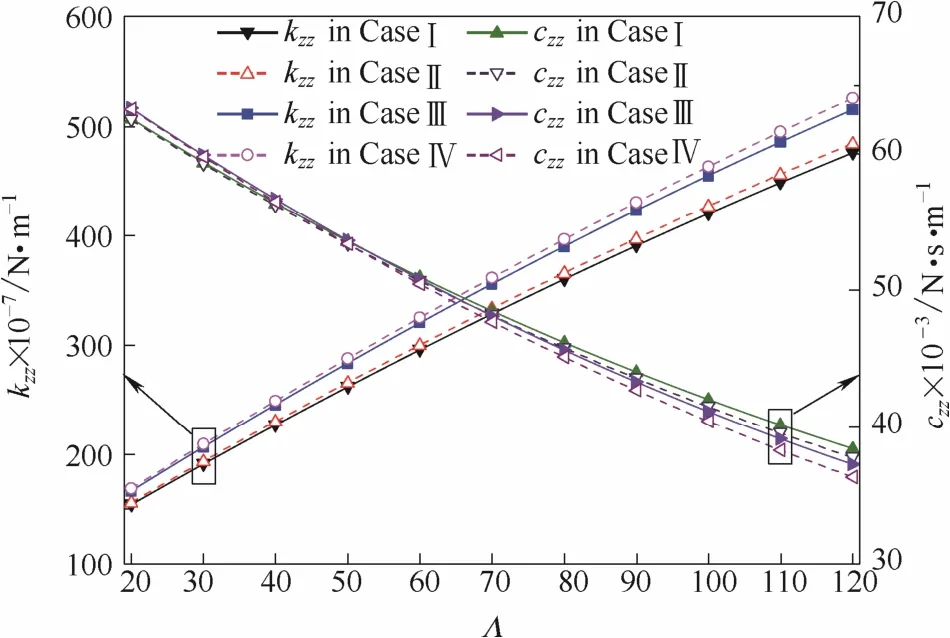
图8 4种计算模型中有量纲直接动态刚度、阻尼对比Fig.8 Comparison of dimension dynamic stiffness and damping coefficients in four calculated cases

5.2 频率比Γ的影响

选定压缩数Λ=50，进口压力为20 MPa。螺旋槽干气密封动特性系数随频率比Γ的变化规律分别如图 9、图 10所示。可以看出，在低频率比范围（Γ=0.01～0.5）内动态刚度和动态阻尼几乎保持恒定。随着频率比的增大，动态刚度（Kzz、Kαα、Kαβ）均增大，动态阻尼（Czz、Cαα、Cαβ）均减小，其中动态刚度和动态阻尼在Γ=0.5～10范围内变化幅度非常明显，在Γ＞10以后动态刚度和动态阻尼的变化幅度趋于平缓。文献[30]指出，对于密封-转子系统，直接阻尼越大越有利于密封的稳定。因此从阻尼的角度出发，外界扰动频率越低，干气密封越容易趋于稳定，这同样符合端面气膜密封稳定性分析和实际运行的结果。

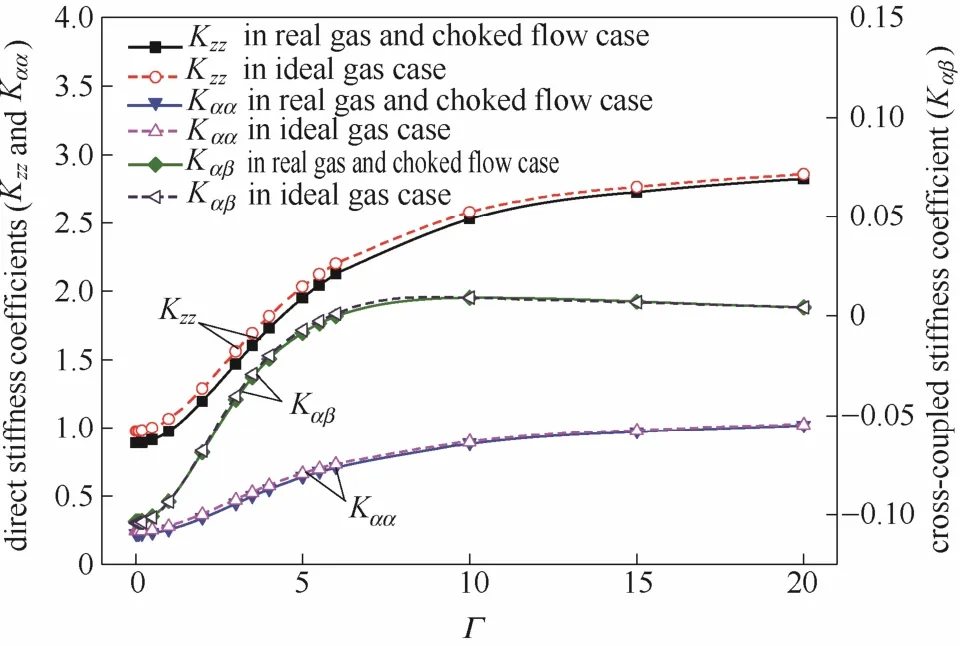
图9 频率比对动态刚度的影响Fig.9 Dynamic stiffness coefficients vary with frequency ratio

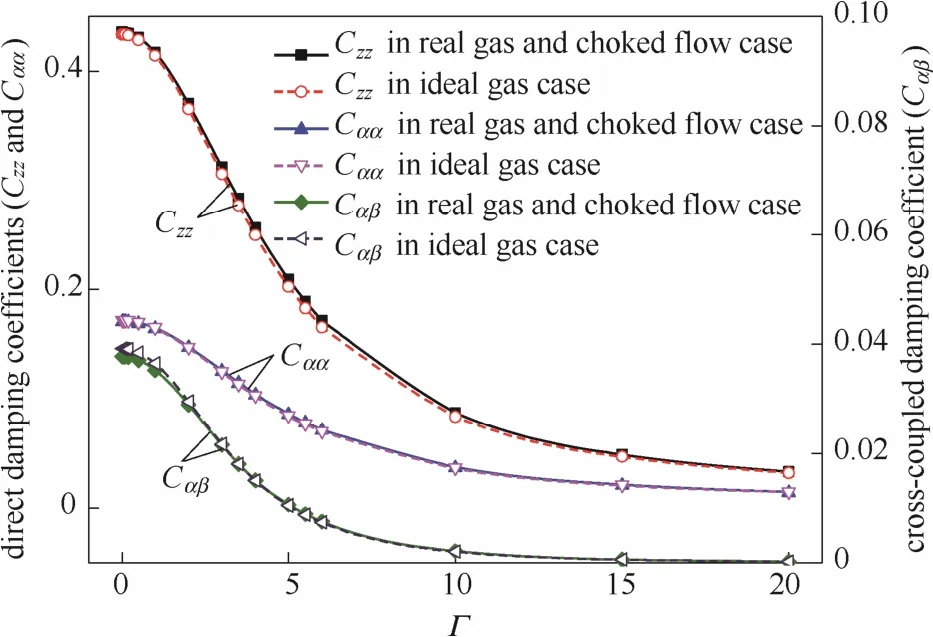
图10 频率比对动态阻尼的影响Fig.10 Dynamic damping coefficients vary with frequency ratio

从以上两图中还可以看出，不同频率比下，考虑实际气体、阻塞流效应模型中的气膜动态刚度系数比理想气体、强制出口压力边界模型中的动态刚度小，动态阻尼则表现出相反的变化趋势。在所研究的频率比范围内，对于动态气膜刚度（Kzz、Kαα、Kαβ），两种模型之间的平均误差分别为 7.04%、8.64%和7.23%，最大误差分别为9.03%、11.7%和18.8%；对于动态气膜阻尼（Czz、Cαα、Cαβ），两种模型之间的平均误差分别为 1.87%、1.29%和2.41%，最大误差分别为4.45%、3.55%和6.26%。对比以上两组误差，显然实际气体效应和阻塞流效应对动态刚度的影响更为显著。

5.3 进口压力po的影响

选定频率数σ=100，压缩数Λ=50。不同进口压力下的动态气膜刚度变化如图11所示。可以看出随着进口压力的增大，就绝对值而言，3种动态气膜刚度均持续增大，且在高压范围内，3种动态气膜刚度的增大幅度均变缓，其中角向直接动态刚度Kαα曲线近似水平。三者的增长幅度并不相同，其中以Kzz最大，Kαβ次之，Kαα最小。相较于理想气体、强制压力出口边界条件，实际气体和阻塞流效应使气膜动态刚度减小。此外，随着进口压力的增大，实际气体效应和阻塞流效应对气膜动态刚度的影响越发明显，即考虑实际气体效应、阻塞流效应和理想气体、强制压力出口边界两种模型间的动态刚度之差随进口压力的增大而增大，说明进口压力增大会导致实际气体效应、阻塞流效应对气膜动态刚度的影响逐渐变强。当进口压力为20 MPa时，两种模型之间动态气膜刚度（Kzz、Kαα、Kαβ）的误差分别为8.46%、10.7%和0.25%。

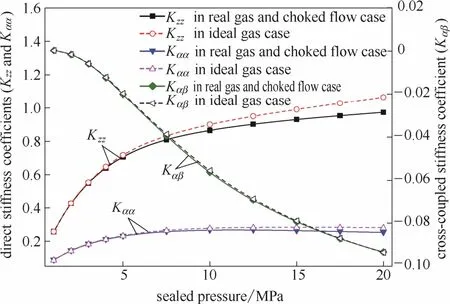
图11 进口压力对动态刚度的影响Fig.11 Dynamic stiffness coefficients vary with sealed pressure

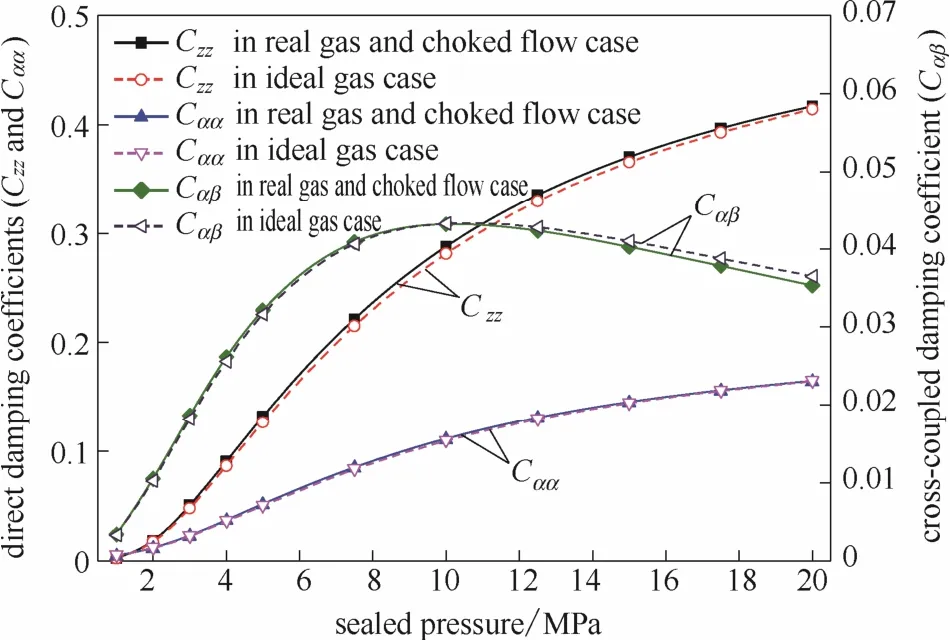
图12 进口压力对动态阻尼的影响Fig.12 Dynamic damping coefficients vary with sealed pressure

不同进口压力下的动态气膜阻尼变化如图 12所示。从图中可以看出直接动态阻尼（Czz、Cαα）随进口压力的增大而增加，其增大幅度逐渐变缓；在1～10 MPa范围内角向交叉耦合阻尼系数Cαβ表现出与直接动态阻尼相同的趋势，随着进口压力的进一步增加，Cαβ逐渐减小。相较于理想气体、强制压力出口边界条件，实际气体效应和阻塞流效应使直接气膜动态阻尼略微变大，但是对于角向交叉阻尼，则呈现出较复杂的变化规律，这可能与外界干扰频率较大有关，具体原因还须进一步的探讨。两种模型之间动态气膜阻尼（Czz、Cαα、Cαβ）的平均误差分别为4.08%、2.07%和1.82%，最大偏差分别为12.6%、3.65%、3.25%。

对于某一特定的动特性系数，在1～3 MPa范围内两种模型中的动特性系数曲线几乎重合，这是由于在此进口压力范围内，密封间隙的出口并没有阻塞流出现，且实际气体效应在此压力范围内可以忽略的缘故。

6 结 论

（1）相较于理想气体和强制出口压力边界模型，实际气体效应和阻塞流效应使氢气螺旋槽干气密封的直接动态气膜刚度减小，使直接动态气膜阻尼增大。针对算例，频率比Γ在0.01～20范围内，两种效应使轴向动态气膜刚度Kzz平均减小了7.04%，最大减少了 9.03%；使轴向动态气膜阻尼Czz平均增大了约1.87%，最大增幅达到4.45%。

（2）实际气体效应和阻塞流效应对动态气膜刚度的影响随压缩数、进口压力的增大而增强。针对计算案例，轴向动态气膜刚度随压缩数变化的最大增幅达到 9.52%、随进口压力增加的最大增幅达8.46%。在低压范围（1～3 MPa）内，两种模型中的刚度曲线几乎重合，可以忽略两种效应的影响。

（3）针对所研究工况，与理想气体和强制边界条件相比，实际气体效应和阻塞流效应使动态气膜阻尼发生改变。压缩数Λ在20～120范围内，动态气膜阻尼（Czz、Cαα、Cαβ）的平均偏差分别为 2.28%、1.93%、2.79%；最大偏差分别为5.77%、5%、3.91%。进口压力1～20 MPa范围内，3种气膜阻尼的平均偏差分别达到4.08%、2.07%、1.82%，最大偏差分别为12.6%、3.65%、3.25%。

[1]程海峰,王为民,王艳东,等.TM02D型串联式干气密封在重整循环氢气压缩机上的应用[J].润滑与密封,2010,35(12)：119-122.CHENG H F,WANG W M,WANG Y D,et al.Application of TM02D-tandeming dry gas seal on reforming circulation hydrogen compressor[J].Lubrication Engineering,2010,35(12)：119-122.

[2]THOMAS S,BRUNETIERE N,TOUMERIE B.Numerical modeling of high pressure gas face seals[J].Journal of Tribology,2006,128(2)：241-242.

[3]产文,宋鹏云,毛文元,等.螺旋槽干气密封端面气膜温度场的数值分析[J].排灌机械工程学报,2015,33(5)：422-428.CHAN W,SONG P Y,MAO W Y,et al.Numerical an alysis of temperature field of gas film in spiral groove dry gas seal[J].Journal of Drainage and Irrigation Machinery Engineering,2015,33(5)：422-428.

[4]宋鹏云,产文,毛文元,等.实际气体效应对螺旋槽干气密封性能影响的数值分析[J].排灌机械工程学报,2015,33(10)：874-881.SONG P Y,CHAN W,MAO W Y,et al.Numerical analysis on effect of real gas on spiral groove dry gas seal performance[J].Journal of Drainage and Irrigation Machinery Engineering,2015,33(10)：874-881.

[5]王衍,孙见君,陶凯,等.T型槽干气密封数值分析及槽型优化[J].摩擦学学报,2014,34(4)：420-427.WANG Y,SUN J J,TAO K,et al.Numerical analysis of T-groove dry gas seal and groove optimization[J].Tribology,2014,34(4)：420-427.

[6]ZUK J,LUDWIG L P,JOHNSON R L.Compressible flow across shaft face seals[C]//Fifth International Conference on Fluid Sealing.Coventry.England：BHRA,1971：Paper H6.

[7]ARGHIR M,DEFAYE C,FRENE J.The Lomakin effect in annular gas seals under choked flow conditions[J].Journal of Engineering for Gas Turbines & Power,2007,129(4)：1028-1034.

[8]THOMAS S,BRUNETIERE N,TOUMERIE B.Thermoelastohydrodynamic behavior of mechanical gas face seals operating at high pressure[J].Journal of Tribology,2007,129(4)：841-850.

[9]马春红,白少先,彭旭东,等.螺旋槽端面微间隙高速气流润滑密封特性[J].摩擦学学报,2015,35(6)：699-706.MA C H,BAI S X,PENG X D,et al.Properties of high speed airflow lubrication in micro-clearance of spiral-groove face seals[J].Tribology,2015,35(6)：699-706.

[10]THATTE A,ZHENG X.Hydrodynamics and sonic flow transition in dry gas seals[C]//Proceedings of the ASME Turbo Expo.Fairfield,United States：American Society of Mechanical Engineers,2014.

[11]江锦波.高速干气密封端面型槽仿生设计与实验研究[D].杭州：浙江工业大学,2016.JIANG J B.Theoretical and experimental study of the bionic design of grooved surface of a high speed dry gas seal[D].Hangzhou：Zhejiang University of Technology,2016.

[12]MILLER B A,GREEN I.Semi-analytical dynamic analysis of spiral-grooved mechanical gas face seals[J].Journal of Tribology,2003,125(2)：403-413.

[13]宋鹏云,胡晓鹏,许恒杰,等.实际气体对T槽干气密封动态特性的影响[J].化工学报,2014,65 (4)：1344-1352.SONG P Y,HU X P,XU H J,et al.Effect of real gas on dynamic T-groove dry gas seal[J].CIESC Journal,2014,65 (4)：1344-1352.

[14]WANG W,LIU Y,JIANG P.Numerical investigation on influence of real gas properties on nonlinear behavior of labyrinth seal-rotor system[J].Applied Mathematics & Computation,2015,263：12-24.

[15]刘雨川.端面气膜密封特性研究[D].北京：北京航天航空大学,2000.LIU Y C.Study on the characteristics of gas film face seal[D].Beijing：Beihang University,2000.

[16]CHEN H,ZHENG J,XU P,et al.Study on real-gas equations of high pressure hydrogen[J].International Journal of Hydrogen Energy,2010,35(7)：3100-3104.

[17]苏长荪.高等工程热力学[M].北京：高等教育出版社,1987：361-362.SU C S.Advanced Thermodynamics[M].Beijing：Higher Education Press,1987：361-362.

[18]刘晖.实际气体温度绝热指数和容积绝热指数的计算[J].石油化工高等学校学报,2000,13(4)：42-45.LIU H.Calculation of the isentropic temperature change exponent and isentropic volume change exponent of real gas[J].Journal of Petrochemical Universities,2000,13(4)：42-45.

[19]邓成香,宋鹏云,马爱琳.干气密封的实际气体焦耳-汤姆逊效应分析[J].化工学报,2016,67(9)：3833-3842.DENG C X,SONG P Y,MA A L.Analysis of Joule-Thomson effect of real gas system sealed by dry gas[J].CIESC Journal,2016,67(9)：3833-3842.

[20]许恒杰,宋鹏云.三自由度微扰下的静压干气密封动态特性分析[J].排灌机械工程学报,2017,35(1)：56-64.XU H J,SONG P Y.Analysis on dynamic characteristics of aerostatic dry gas seals with three degrees of freedom perturbation[J].Journal of Drainage and Irrigation Machinery Engineering,2017,35(1)：56-64.

[21]LIU Y,SHEN X,XU W.Numerical analysis of dynamic coefficients for gas film face seals[J].Journal of Tribology,2002,124(4)：743-754.

[22]刘雨川,徐万孚,王之栎,等.端面气膜密封动力特性系数的计算[J].清华大学学报(自然科学版),2002,42(2)：185-189.LIU Y C,XU W F,WANG Z L,et al.Dynamic coefficients for gas film face seal[J].J.Tsinghua Univ.(Sci.& Technol.),2002,42(2)：185-189.

[23]黄平,许兰贵,孟永钢,等.求解磁头/磁盘超薄气膜润滑性能的有效有限差分算法[J].机械工程学报,2007,43(3)：43-49.HUANG P,XU L G,MENG Y G,et al.Effective finite difference method to calculate lubricating performances of ultra-thin gas film of magnetic head/disk[J].Chinese Journal of Mechanical Engineering,2007,43(3)：43-49.

[24]LEBECK A O.Principles and Design of Mechanical Face Seals[M].John Wiley & Sons,Inc.,1991：371.

[25]RUAN B.Numerical modeling of dynamic sealing behaviors of spiral groove gas face seals[J].Journal of Tribology,2002,124(1)：186-195.

[26]RUAN B.A semi-analytical solution to the dynamic tracking of non-contacting gas face seals[J].Journal of Tribology,2002,124(1)：196-202.

[27]陈源,彭旭东,李纪云,等.螺旋槽结构参数对干气密封动态特性的影响研究[J].摩擦学学报,2016,36(4)：397-405.CHEN Y,PENG X D,LI J Y,et al.The influence of structure parameters of spiral groove on dynamic characteristics of dry gas seal[J].Tribology,2016,36(4)：397-405.

[28]刘向锋,徐辰,黄伟峰.基于半解析法的极端工况干气密封动态特性研究与参数设计[J].清华大学学报(自然科学版),2014,54(2)：223-228.LIU X F,XU C,HUANG W F.Analysis and parametric design of the dynamics of a dry gas seal for extreme operating conditions using a semi-analytical method[J].J.Tsinghua Univ.(Sci.& Technol.),2014,54(2)：223-228.

[29]ZIRKELBACK N.Parametric study of spiral groove gas face seals[J].Tribology Transactions,2000,43(2)：337-343.

[30]晏鑫,蒋玉娥,李军,等.迷宫密封转子动力学特性的数值模拟[J].热能动力工程,2009,24(5)：566-570.YAN X,JIANG Y E,LI J,et al.Numerical calculation of dynamic coefficients for gas film cylinder seal[J].Journal of Engineering for Thermal Energy and Power,2009,24(5)：566-570.

date:2017-05-31.

Prof.SONG Pengyun,songpengyunkm@sina.com

supported by the National Natural Science Foundation of China (51465026).

Dynamic characteristics of spiral groove dry gas seals with consideration of hydrogen real gas and choked flow effects

XU Hengjie1,2,SONG Pengyun1,MAO Wenyuan1,DENG Qiangguo1
(1Faculty of Chemical Engineering,Kunming University of Science and Technology,Kunming650500,Yunnan,China;2Faculty of Environmental Science and Engineering,Kunming University of Science and Technology,Kunming650500,Yunnan,China)

The exit pressure boundary was determined by Chen’s real gas equation of hydrogen and choked flow condition of gas exit speed reaching to the sound speed.Then,dynamic characteristics of spiral groove dry gas seal (S-DGS) at various operating parameters was analyzed by perturbation method,and compared to those of ideal gas and coercive exit pressure boundary models.The results show that real gas and choked flow effects should be taken into account for studying dynamic characteristics of S-DGS at high pressure.Both effects reduced direct stiffness coefficients of hydrogen S-DGS but increased direct damping coefficients.The influence of these two effects on dynamic gas film stiffness gradually enhanced with the increase of squeeze number and inlet pressure.In addition,when frequency ratio was varied,these two effects had a significant influence on gas film dynamic stiffness but minimal influence on gas film dynamic damping.Compared to models of ideal gas and coercive pressure boundary condition at the studied operating circumstance,these two effects caused three gas film dynamic damping coefficients (Czz,Cαα,Cαβ) by mean standard deviations of 2.28%,1.93%,2.79% when squeeze number is variable and 4.08%,2.07%,1.82% when inlet pressure is variable.

spiral groove dry gas seal; dynamic characteristics; real gas; choked flow; numerical analysis

S 277.9；TH 136

A

0438—1157（2017）12—4675—10

10.11949/j.issn.0438-1157.20170704

2017-05-31收到初稿，2017-07-07收到修改稿。

联系人：宋鹏云。

许恒杰（1989—），男，博士研究生。

国家自然科学基金项目（51465026）。