理解数学是进行有效教学设计的前提

江苏省无锡市立人高级中学 (214161)

郑宝生 赵 勤

理解数学是进行有效教学设计的前提

江苏省无锡市立人高级中学 (214161)

郑宝生 赵 勤

要上好一堂课，一旦教师确定后，关键在于教学设计．我们很赞赏章建跃先生的“三个理解”，其中，“理解数学”是进行有效教学设计的前提．作为教师，不仅要理解所教内容“是什么”，还要弄清知识的整个体系及知识的前后联系，挖掘数学知识所蕴含的思想方法及解题过程中所反映的思维策略．

1.理解数学体系，让学生体会到数学的研究方法

我们的课堂教学既要教学生学习每个知识，又要让学生理解每一章的知识结构，并体会到数学自身的知识体系以及研究方法，而对数学知识体系和研究方法的认知，影响学生对数学整体的认知和从数学角度看待问题的数学意识，正如普通高中《数学课程标准》所谈到的：“通过类比、联想、知识的迁移和应用等方式，使学生体会知识之间的有机联系，感受数学的整体性，进一步理解数学的本质，提高解决问题的能力”．所以说数学教师要有较高的数学素养，较高的理解水平，能够从整个数学知识体系的角度理解数学，抓住主要知识，厘清从属关系，形成逻辑结构．

在高中数学的《平面向量》一章中，最重要的是平面向量基本定理，换句话说就是平面向量的线性表示．如果要追问，平面向量线性表示的基础是平面向量的加减和数乘运算，而加减数乘运算的基础是平面向量的大小和方向；如果看其变化，平面向量线性表示的特殊情况是平面向量的坐标表示，它使得平面向量的内容更加丰富，平面向量数量积的应用更加广泛．厘清其中的关系，做到心中有数，才能设计好课堂教学．例如，苏教版普通高中数学必修4《向量的概念与表示》的教材中，先给出向量的定义，讨论了零向量和单位向量后，给出思考：平面直角坐标系内，起点在原点的单位向量，它们终点的轨迹是什么图形？然后定义平行向量，再定义相等向量，这样，从知识的角度讲，割裂了知识间的内在联系，从学生心理的角度看，缺少具体的事例和必要的情境，平行向量出现的有点突然，不够清晰，不够自然．站在数学知识体系的高度来看待向量，抓住向量的大小和方向这两根主要线索，引导学生从定义、表示、大小特殊和方向特殊这样的顺序展开，整合设计流程如下：(1)向量的定义：大小、方向(两个要素)；(2)向量的表示(略)；(3)大小特殊的向量——零向量、单位向量；(4)方向特殊的向量——同向向量、反向向量；(5)同向向量的特殊情况——相等向量；(6)反向向量的特殊情况——相反向量．最后让学生讨论“怎样的向量才能称之为平行向量？”，如此设计，一方面没有打破数学知识体系的逻辑性和整体性，另一方面，条理更清晰，学生容易参与进来，不仅有益于“平行向量”概念的理解，而且能让学生体会到数学自身的逻辑体系，能更好的理解数学，把握数学的本质．

2.理解数学概念，让学生感受到数学的形成过程

3.理解数学解题，让学生领悟解题背后的策略与思想

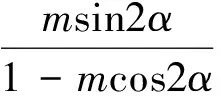
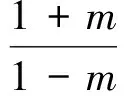
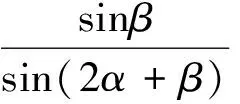
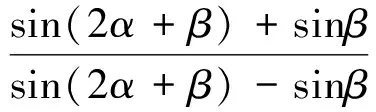
=tan(α+β)．

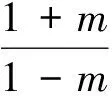
在这里并不想论述一题多解，也不想阐释各种变式，是想说明，对于教师应该如何理解这三种不同的解题过程，解法一是先化简后求值，解法二是代入消元，解法三是变角法．我们要追问三种不同解法的背后有着怎样的支撑，它们体现了一个共同的解题策略：“减少未知量”，体现了求简的思想．在数学解题中，所有的消元法都是在减少未知量，所有的换元法都能使运算简单，我们所说的化简就是化繁为简的过程，都反映了人们求“简“的一种精神追求．其次，三种不同解法有着怎样的考量．解法一对已知条件的化简，化简不到位无法与目标对接，化简过头又会离目标太远，火候很难掌控．如果没有一点经验和思想的支撑，是很难找到解题思路的．我们抓住目标中只有一个角β，所以不顾一切地用tanα表示tanβ，从而消去角β，最后面对的都是tanα，当然能证出来．这样的策略显得比较生硬，给人以顾头不顾尾的感觉，原因是对目标简单、肤浅的感知，导致问题解决过程中运算量增加．解法二也是这样，只是专注于消去m，使得运算量未曾减少．而解法三感知到的是问题的整体，其策略是把条件与结论有机地结合在一起，结论中有角(α+β)、α，按照减少未知角的思路，把已知条件中的角β和2α+β都化为(α+β)、α，所以解起来很轻松．最后，从学生的角度看待三种解法，他们更愿意接受解法一和解法二，因为代入消元法是初中学生熟知的方法，而他们的计算能力却达不到要求，导致证明困难．然而有了解法一的消去角β，才容易联想到解法二的消去m，通过解法二中sin(2α+β)±sinβ的化简过程，可以轻松地整理出解法三的思路．“变角”即角的变换，是本章的主体内容——三角变换的重要变换，需要学生理解并掌握．因此，数学解题后，教师需要引导学生思考，不同解法有怎样的差异？产生这些差异的原因是什么？它们之间有着怎样的联系？不同解法的背后有怎样的思想支撑？才能让我们的解题更有效果．

作为一个数学教师必须要理解好数学，理解数学的知识体系和研究方法；理解数学的每一个概念及其本质属性；理解数学解题的每一个步骤和蕴含的思想方法．当然，还要理解学生，让我们的课堂教学更有针对性；要理解教学，让我们的课堂教学更符合规律，更有实效；理解人生，让我们的课堂教学更有哲理，内涵丰富更有教育意义．

[1]中华人民共和国教育部制订．普通高中数学课程标准(实验)[M]．北京：人民教育出版社，2003．

[2]王华民，郑宝生，阮必胜．教师“贴地而行”，学生“翩翩起舞”[J]．数学通报，2014．5.

[3]梁莉娟，郑宝生，王华民．遵循三个理解的问题探究，彰显学生的主体地位[J]．中国数学教育(高中版)2017．1-2.