平常题“非常”运用提升学生核心素养——一道高三模拟试题教学为例

浙江省上虞市城南中学 (312300)

王春霞

平常题“非常”运用提升学生核心素养
——一道高三模拟试题教学为例

浙江省上虞市城南中学 (312300)

王春霞

数学核心素养主要包含数学抽象、逻辑推理、数学建模、直观想象、数学运算、数据分析六方面.培养学生的核心素养是新课改的主旋律，也是新型课堂模式的基本要求.在高三的模拟卷中，不少试题看似平凡，但深入研究则是富有内涵、具有良好教学价值的好题.在教学过程中若能对此类好题展开多角度审视、多方位变式拓展，变“习题”为“问题”，变“问题”为“课题”，变“讲授”为“悟道”，让学生自己探索研究问题的路径，给学生留足思考空间，让学生经历完整的获得对象——研究性质——应用拓展过程，使学生学会思考，实现能用数学的方式认识问题和解决问题.这样就能让学生从整体上把握高中数学的核心内容、了解知识发展脉络、透析数学思想方法、洞察解题基本规律，促使学生的数学素养得到提升，帮助学生从学习数学的“苦海”中解脱出来，使他们在高考中获得成功.

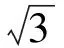
此题来源于笔者所用高三复习综合测试卷,定弦定角是解不定型三角形比较典型、常见的一类问题,虽然该题比较基础，但基础是素养的保证，是以后发展的基石，是高考考查的重点所在，因此笔者打算挖掘此题“可再生资源”，揭示该类题的背景和本质.

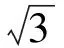
师：变式1中若确定A、C的位置，则B的运动轨迹是什么？

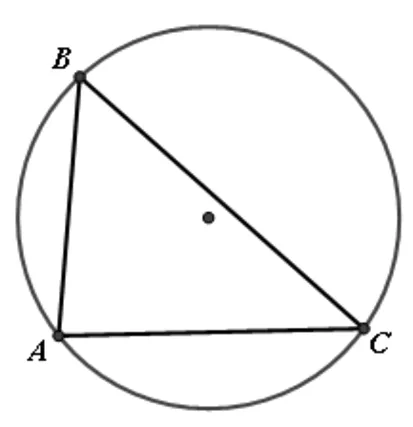
图1

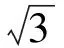
师：理解很对，如果不再给其他条件，我们可以研究哪些问题呢？请同学们思考.(学生思考时教师最好不要过多的提示，应该让学生的思维得到充分发挥，3分钟后请学生说说自己的想法.)

生2：a或c的范围.

师：如何解决？

生3：其实a,c的范围直接从图上可以看出来，比如边长a，当BC过圆心时最大值为4，当B,C趋向于重合时最小值为0，边c也一样.

师：很好！利用图像简洁明了，真是有图有真相！

生4：既然a,c范围可求，那么a±c，a·c范围应该也可求.

师：以a+c为例，请同学试试(给学生5分钟尝试)

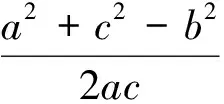
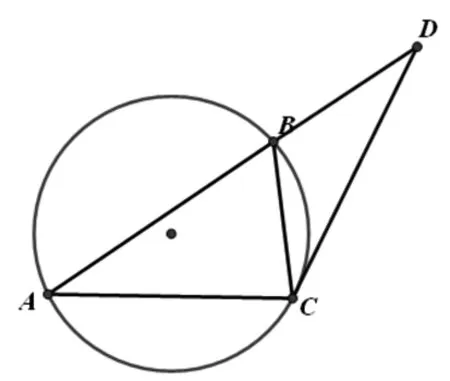
图2

师：这种方法很好，结合图像该三角形还有那些问题一目了然？

生8：面积的最大值，周长的最值等.

师：既然a±c，a·c范围应该也可求，那么……

生9：有关角A,C的一些范围问题也可以求得，比如sinA+sinC,sinA·sinC的取值范围问题.

师：嗯，对！怎么想到的？

生9：由正弦定理得a=2RsinA,b=2RsinB,C=2RsinC,边的范围可求自然对应角的范围也出来了.

师：那么a+λc(λ为常数)最值能求么？

师：那其他两种方法呢？还适用么？

生11：好像不太好用，有变化.

师：那怎办，此两条思路该不该放弃？

生12：老师不用的！生6的方法只要改进一下就好，设a+λc=k,则a=k-λc,代入a2+c2-12=ac，得到(λ2+λ+1)c2-2kλc+k2-12=0,方程有解，判别式Δ≥0，可求得k的范围.

师：非常棒！

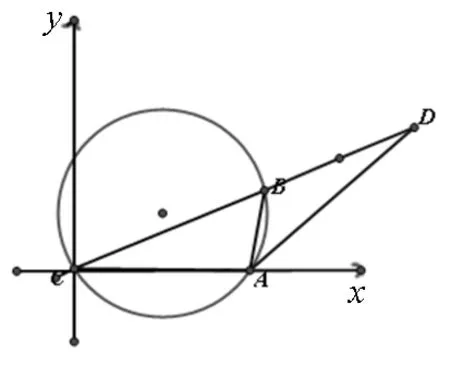
图3

生13：老师我觉得利用图像也可行，如图3，延长CB至D使得BD=λc,在△ABD中，AD2=a2+(λa)2-2·a·(λa)cos120°=(1+λ+λ2)a,∴∠ADP的余弦值可以用λ,a表示，设直线BC斜率为k,直线AD斜率可用k表示，两直线相交求得D的坐标(用参数k表示)，消去参数就得D的轨迹方程.轨迹为圆，那么问题转化为原点到圆上点距离的最大值.

师：叫我刮目相看！真是应验了那句话“只有想不到的，没有做不到的”.整理过程留给大家课后完成.

教室内顿时响起了热烈的掌声，教师把此题的探究又进一步引向深入，学生思维的火花照亮了课堂.

师：前面我们主要探讨已知一角一对边三角形的其余角边范围问题，下面请大家想想模拟试卷的问题还有哪些解决办法？(由于有前面的铺垫，学生很快得到如下解法.)

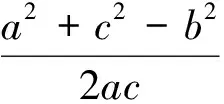
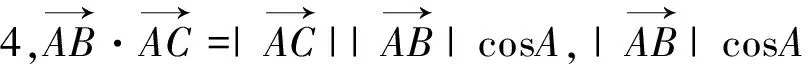
师：三角形中6个基本量，已知一角一对边的不定型问题已经解决.解决此类问题主要利用正余弦定理进行角、边互化，进而把问题转化为函数最值范围问题或者利用图像解决.同学们还想探究什么问题呢？

学生讨论，老师总结：两角，两边及一边一邻角.两角的问题比较简单，不去研究了.一边一邻角问题课后研究.

师：如果已知三角形一个内角，此时的三角形又有什么值得我们研究的呢？

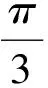
师：大家再试试看.

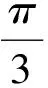
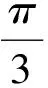
一道填空题，花费了整整一节课时间，尽管一张试卷的讲解不能如期完成，但是学生的核心素养也得到提升，如通过对问题的一题多解、一题多变让学生洞察问题的深层结构，形成优化的认知网络，这种从事物的具体背景中抽象出一般规律和结构就是在发展学生“数学抽象”的核心素养；又如引导学生探究B的运动轨迹的过程可促进发展学生的“直观想象”核心素养；再如由a或c的范围到a±c，a·c的范围再到a+λc的范围的探究过程可促进学生发展“逻辑推理”“数学运算”的核心素养.通过激烈讨论，大胆猜想，小心求证；通过 “怎样想到的”，“如何转化”“有不同想法么”等一系列剥笋式的提问促使学生暴露其思维过程，让学生不仅知其然，且知其所以然.正如G.波利亚说:“一个专心的认真备课的教师能够拿出一个有意义的但又不太复杂的题目,去帮助学生挖掘问题的各个方面,使得通过这道题,就好像通过一道门户,把学生引入一个完整的理论领域.”