复合树的Felicitous性质
张明军,杨思华,姚兵
(1. 兰州财经大学信息工程学院,甘肃 兰州 730020;2. 兰州财经大学陇桥学院,甘肃 兰州 730101;3. 西北师范大学数学与统计学院,甘肃 兰州 730070)
复合树的Felicitous性质
张明军1,杨思华2,姚兵3
(1. 兰州财经大学信息工程学院,甘肃 兰州 730020;2. 兰州财经大学陇桥学院,甘肃 兰州 730101;3. 西北师范大学数学与统计学院,甘肃 兰州 730070)
将多个具有集有序 Felicitous 性质的树上的点与一棵集有序优美树上的点重合,构造出一棵较大的复合树, 经研究计算, 该复合树具有集有序 Felicitous 性质。
复合树; 集有序 Felicitous 标号; 集有序优美标号
图的标号广泛应用于编码理论、通讯网络、物流、同步机码设计、无线电频道分配和读取DNA序列等领域。 优美图是图的标号研究中十分重要的课题之一。1966年, Rosa[1]提出了一个猜想:每一棵树都是优美树。后来,Bermond[2]又提出了猜想:所有龙虾树都是优美树。关于这两个猜想已经有了很多结果, 但是一直没有彻底的解决。Lee等[3]于 1991 年提出了猜想:每一棵树都是 Felicitous 树。该猜想与优美树猜想具有同等的理论价值, 而且具有相同的难度, 都是 NP-hard 问题[4-13]。对于数学猜想的进攻, 导致图的标号迅速发展成为当今图论学科中十分活跃的分支。
1 预备知识
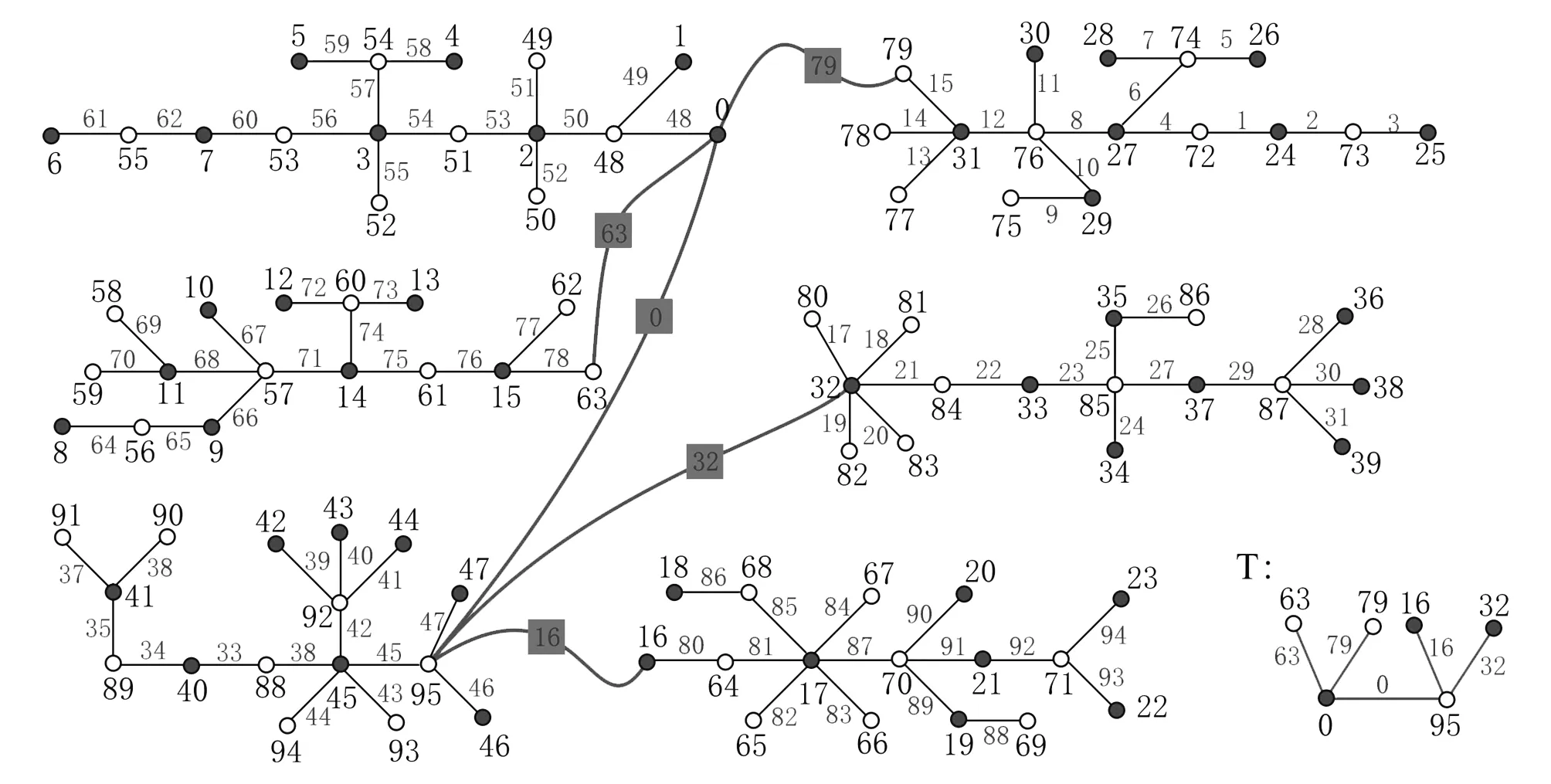
本文涉及的图均为有限、无向简单图。文中没有定义的术语和符号均来自文献[14]。为叙述简便,我们把一个有p个顶点q条边的连通图记为(p,q)-图。记号[m,n]表示非负整数集合{m,m+1,m+2,…,n},其中m和n均为整数,且满足0≤m 定义1 设G是(p,q)-图,若存在一个单射f:V(G)→[0,q],使得边标号集合{f(uv)|uv∈E(G)}=[0,q-1],其中边标号为f(uv)=f(u)+f(v)(modq),那么称G是Felicitous图,并称f是G的一个Felicitous 标号。进一步,设(X,Y)是二部图G的顶点集的一个二部划分,如果G有一个Felicitous 标号f,使得 max{f(x)|x∈X} (以下简记为f(X) 则称G是集有序 Felicitous 图,也称f是G的一个集有序 Felicitous 标号。 对于定义1中的图G和Felicitous标号f,以下简记顶点标号集合为f(V(G))={f(u)|u∈V(G) },边标号集合为f(E(G))={f(u)+f(v)|uv∈E(G) },以及f(E(G))(modq)={f(uv)|uv∈E(G) }。 定义2 设G是(p,q)-图,若存在一个单射f:V(G)→[0,q],使得边标号集合{f(uv)|uv∈E(G) }=[1,q],其中边标号为f(uv)=|f(u)-f(v)|,那么称G是优美图,并称f是G的一个优美标号。进一步,设(X,Y)是二部图G的顶点集的一个二部划分,若G有一个优美标号f,使得f(X) 定义3 设T,H1,H2,…,Hp是树,|V(T)|=p,V(T)={wi|i∈[1,p] },|V(Hi)|=n,|V(Hi)|={ui,j|i∈[1,p],j∈[1,n] },将T的顶点wi(i∈[1,p])与树Hi中的一个ui,j0(j0∈[1,n])重合,得到的图G叫做复合树,特记为G=[T;H1,H2,…Hp]。 定理1 设树H1,H2,…,H|V(T)|有集有序 Felicitous 标号,树T是集有序优美树,且其顶点集二部划分(X,Y)满足||X|-|Y||≤1,则复合树[T;H1,H2,…,H|V(T)|]具有集有序 Felicitous 标号。 证明根据定理假设, 树T是有p个顶点的集有序优美树,其顶点集二部划分为(X,Y),其中||X|-|Y||≤1,X={w1,w2,…wl},Y={wl+1,wl+2,…wp}。树T有一个集有序优美标号f,使得f(wi)=i-1,i∈[1,p],并且f(X) 令|V(Hk)|=n,则有s+t=n,且有 利用f定义T的一个标号f′如下:f′(wi)=f(wi)+1=i,i∈[1,p]。由p的奇偶性来定义复合树[T;H1,H2,…Hp]的一个标号h。 情形Ⅰ 当p=2β+1时,从而有||X|-|Y||=1。令|X|=|Y|+1。我们定义复合树[T;H1,H2,…Hp]的标号h如下: (i) 当k∈[1,β+1]时,令 n(k-1)+i-1,i∈[1,s]; n(β+k-1)+s+j-1,j∈[1,t] (ii) 当l∈[β+2,2β+1]时, 令 n(3β+2-l)+s-i,i∈[1,s]; n(2β+2-l)-j,j∈[1,t] 经过计算得h(V([T;H1,H2,…,H2β+1]))= [0,n(2β+1)-1],且有 {h(uk,i):k∈[1,β+1],i∈[1,s]}∪{h(vl,j): l∈[β+2,2β+1],j∈[1,t]}= [0,nβ+s-1]=X*; {h(vk,j):k∈[1,β+1], j∈[1,t]}∪{h(ul,i):l∈[β+2,2β+1], i∈[1,t]}=[nβ+s,n(2β+1)-1]=Y* 注意到,若(X*,Y*)是复合树[T;H1,H2,…Hp]的顶点集二部划分,则有h(X*) 下面,证明标号h是复合树[T;H1,H2,…Hp]的集有序Felicitous 标号。 当k∈[1,β+1],i∈[1,s]和j∈[1,t]时,Hk的每一条边uk,ivk,j满足 h(uk,ivk,j)=h(uk,i)+h(vk,j)= n(β+2k-2)+s+i+j-2, n(β+2k-1)+s-2] 当l∈[β+2,2β+1],i∈[1,s]和j∈[1,t]时,Hl的每一条边ul,ivl,j满足 h(ul,ivl,j)=h(ul,i)+h(vv,j)= n(5β-2l+4)+s-i-j, n(5β-2l+4)+s-2], h(E(H1,H2,…,H2β+1))= [nβ+s,n(3β+1)+s-2]N* 此处 N*=[n(β+1)+s-1, n(β+2)+s-1,n(β+3)+s-1,…, n(3β-1)+s-1,3nβ+s-1] 1) 对固定的i0∈[1,s],将Hm(m∈[1,2β+1])的顶点um,i0与树T的顶点wm重合。对k∈[1,β+1],l∈[β+2,2β+1],关于复合树[T;H1,H2,…H2β+1]的边wkwl有 f′(wkwl)=f′(wk)+f′(wl)=h(uk,i0)+ h(ul,i0)=n(3β+k-l+1)+s-1 经过计算得 f′(wkwl)∈[n(β+1)+s-1,n(β+2)+s-1, n(β+3)+s-1,…,n(3β-1)+s-1, 3nβ+s-1]=N* 2) 对固定的j0∈[1,t],将Hm(m∈[1,2β+1])的顶点vm,j0与树T的顶点wm重合。对k∈[1,β+1],l∈[β+2,2β+1],计算复合树[T;H1,H2,…H2β+1]的边wkwl,得到 f′(wkwl)=f′(wk)+f′(wl)= h(vk,j0)+h(vl,j0)= n(3β+k-l+1)+s-1 经过计算得 f′(wkwl)∈ 综上得,边标号集合h(E([T;H1,H2,…Hp]))=[nβ+s,n(3β+1)+s-2]。因此, h(E([T;H1,H2,…Hp]))· 以及 h(X*) 故当p是奇数时,标号h是复合树[T;H1,H2,…Hp]的集有序 Felicitous 标号。 情形Ⅱ 当p=2β时,则有||X|-|Y||=0。定义标号h如下: (i) 当k∈[1,β]时, 令 h(uk,i)=n(k-1)+i-1,i∈[1,s]; h(vk,j)=n(β+k-1)+j-1,j∈[1,t] (ii) 当l∈[β+1,2β]时, 令 h(ul,i)=n(3β+1-l)-i,i∈[1,s]; h(vl,j)=n(2β+1-l)-j,j∈[1,t] 用与奇数情形相同的方法, 可得到边标号集合 h(E([T;H1,H2,…Hp]))(mod 2nβ-1)= [0,2nβ-2] 综合情形 1 和情形 2 的讨论, 本定理得证。(图1与图2是解释定理1的两个例子) 图1 解释定理1的一个例子Fig.1 An example for illustrating Theorem 1 图2 解释定理1的另一个例子Fig.2 Another example for illustrating Theorem 1 [1] ROSA A. On certain valuations of the vertices of a graph [J]. Theory of Graphs, 1967: 349-355. [2] BERMOND J C. Graceful graphs, radio antennae and French windmills [J]. Graph Theory & Combinatorics, Pitman London, 1979, 34: 18-37. [3] LEE S M, SCHMEICHEL E, SHEE S C. On felicitous graphs [J]. Discrete Mathematics, 1991, 93(2/3): 201-209. [4] GALLIAN J A. A dynamic survery of graph labeling [J]. The electronic journal of combinatorics, 2009, 12: 42-43. [5] MANICKAM K, MARUDAI M, KALA R. Some results on felicitous labeling of graphs [J]. Journal of Combinatorial Mathematics & Combinatorial Computing, 2012, 81: 273-279. [6] GNANAJOTHI R B. Topics in graph theory [D]. Madurai: Madurai Kamaraj University, 1991. [7] YAO B, CHENG H, YAO M, et al. A note on strongly graceful trees [J]. Ars Combinatoria, 2009, 92:155-169. [8] GRAHAMS R L, SLOANE N J A. On additive bases and harmonious graphs [J]. Siam Journal on Algebraic & Discrete Methods, 2006, 1(1): 382-404. [9] ZHOU X Q, YAO B, CHEN X E, et al. A proof to the odd-gracefulness of all lobsters [J]. Ars Combinatoria, 2012, 103: 13-18. [10] 唐保祥, 任韩. 2类优美图的冠的优美标号[J]. 中山大学学报(自然科学版), 2015, 54(5): 24-27. TANG B X,REN H. Graceful labeling of the corona for two kinds of graceful graphs [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2015, 54(5): 24-27. [11] 赵喜杨, 姚兵. 探讨树的(k,d)-边魔幻全标号[J]. 中山大学学报(自然科学版), 2016, 55(6): 67-73. ZHAO X Y, YAO B. Probing (k,d)-edge magic total labellings of trees [J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(6): 67-73. [12] 张明军,赵喜杨,姚兵.(2m+1,1)-p-树的二分强优美性和二分强奇优美性[J]. 应用数学学报, 2016, 39(3): 419-428. ZHANG M J, ZHAO X Y, YAO B. On bipartite strongly gracefulness and bipartite strongly odd-gracefulness of (2m+1,1)-p-trees [J]. Acta Mathematicae Applicatae Sinica, 2016, 39(3): 419-428. [13] 吴跃生. 图Fn,4(r1,r2,…,r3n+1)的交错标号[J]. 中山大学学报(自然科学版), 2016, 55(4):11-14. WU Y S. The alternating labeling of the graphFn,4(r1,r2,…,r3n+1)[J]. Acta Scientiarum Naturalium Universitatis Sunyatseni, 2016, 55(4):11-14. [14] BONDY J A, MURTY U S R. Graph theory with applications [M]. London: The MaCmillan Press ltd, 1976. TheFelicitouspropertyofcompositetrees ZHANGMingjun1,YANGSihua2,YAOBing3 (1. School of Information Engineering, Lanzhou University of Finance and Economics, Lanzhou 730020, China;2. Longqiao college, Lanzhou University of Finance and Economics, Lanzhou 730101, China;3. College of Mathematics and Statistics, Northwest Normal University, Lanzhou 730070, China) Multiple trees with set-ordered Felicitous property are coupled with a vertex on set-ordered graceful trees, and a larger composite tree is constructed. It is shown that, the composite tree has set-ordered Felicitous property. composite trees; set-ordered felicitous labelling; set-ordered graceful labelling 10.13471/j.cnki.acta.snus.2017.06.008 2017-03-01 国家自然科学基金(61363060, 61662066);兰州财经大学高等教育教学改革研究重点项目(LJZ201707);甘肃省高等学校科研项目(2017A-047) 张明军(1973年生),男;研究方向图的标号与复杂网络;E-mail: zhangmjlz@163.com O157.5 A 0529-6579(2017)06-0060-04 DOI:10.13471/j.cnki.acta.snus.2017.06.0092 主要结论及其证明
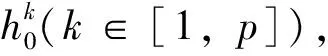

[n(β+1)+s-1,n(β+2)+s-1,
n(β+3)+s-1,…,n(3β-1)+s-1,
3nβ+s-1]=N*
(modn(2β+1)-1)=[0,n(2β+1)-2],
h(V([T;H1,H2,…H2β+1]))=[0,n(2β+1)-1]