浅谈立体几何中直线与平面

李雪鹏

浅谈立体几何中直线与平面

李雪鹏

大理州巍山县第二中学 云南大理 672400

在“直线与平面”内容中，为了研究直线与直线之间，直线与平面之间，平面与平面之间的各种关系，引进了一些基本概念和数学方法，例如“异面直线”，“直线与平面所成的角”、“二面角”等概念，反证法、同一法等方法，对于这类特定的概念理解不准确，对这些方法的掌握存在某些缺陷，解题时就容易出错。

下面通过几例，对产生错误的解法进行分析，研究纠正错误的方法，从中吸取有益的教训，以加深对知识的理解，提高解题能力。

例1证明；斜线上任意一点在平面上的射影，一定在斜线的射影上。

错解如图,对于平面 ，直线AB是垂线，垂足B是点A的射影；直线AC是斜线，C是斜足，直线BC是斜线AC的射影。

在AC上任取一点P，过P作P0⊥ 交BC于0，

∴点P在平面 上的射影在BC上。

点击 这样的证明似乎有点道理，事实上这些点也是在这条斜线在该平面的射影上，但仔细分析，这些点在这条斜线在该平面的射影上的理论根据不足，过点P作P0⊥ 交BC于0，恰恰是本题要证明的，是一种易犯的逻辑错误，许多同学在解题中往往错而不觉，对此应引起警觉。

正解 AC是平面 的斜线，点C是斜足，AB⊥ ，点B是垂足，则BC是AC在平面 上的射影。

在AC上任取一点P，过点P作PO⊥ ,垂足为0。

∴AB⊥ ，∴P0∥AB，

∵点P在A、B、C三点确定的平面上，因此，P0 平面ABC，

∴0∈BC。

例2已知 、是两个不重合的平面，①若平面 ⊥平面 ，平面 ⊥平面 ，则平面 ∥平面 ；②若平面 内不共线的三个点到平面 的距离相等，则平面 ∥平面；

③a、b是平面 内的两条直线，且a∥ ，b∥ ，则平面 ∥平面；

以上正确命题的个数为( )。

(A)O个 (B)1个 (C)2个 (D)3个

错解 三个命题都正确，选(D)。

点击 产生错误的原因是对问题不能全面的分析，缺乏把握空间元素位置关系的能力，不是用特殊代替一般，就是用一般统盖“特殊”。如判断①、②是真命题，只是考虑了图1与图2的情况，而忽略了图3与图4的情况。

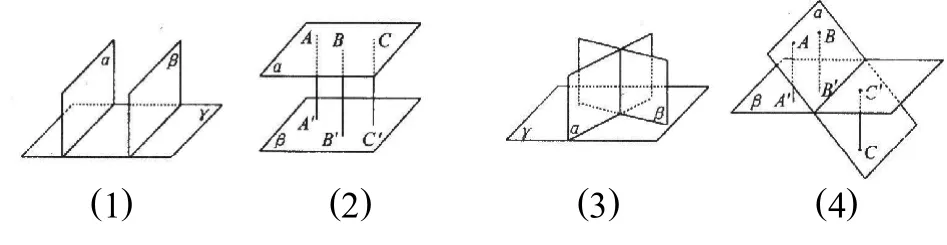
而判断③是真命题，则是对平面与平面平行的判定定理：“如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行”没有真正理解，用任意两条直线代替了定理中的特指条件“两条相交直线”。

正解 因为三个命题都不正确，所以选(A)。

例3在正方体ABCD—A1B1C1D1中，求它的对角线BD1与平面A1B1CD所成的角。

错解 连结A1C交BD1于E，则∠D1EA为BD1与平面A1B1CD所成角，设正方体的边长为a，

在△A1ED1中，由余弦定理得

点击 以上证法的错误在于，∠A1ED1不是直线BD1与平面A1B1CD所成的角。平面的一条斜线与它在平面上的射影所成的锐角，叫做这条直线与这个平面所成的角，本题中D1A1不垂直于平面 A1B1CD，所以 A1E不是 D1E在平面A1B1CD内的射影。正是对“直线在平面内的射影”这个概念理解不清，导致了以上错误，所以在解此类题时，一定要先找出斜足，再作出垂足，垂足与斜足连线才得射影。

正解 ∵A1B1⊥平面A1ADD1,又 A1B1平面A1B1CD

∴平面A1ADD1⊥平面A1B1CD。

连结AD1交A1D于O,则D1O⊥A1D,

∴D1O⊥平面A1B1CD。

连A1C交BD1于E，连OE，则OE为D1E在平面A1B1CD内的射影,

∴∠D1EO为BD1与平面A1B1CD所成的角。

∴ ∠D1E0=aretan，即BD1与平面A1B1CD所成的角为arctan。