基于横摆角速度反馈的三轮全转向电动叉车转向研究

邵新明,肖本贤

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

基于横摆角速度反馈的三轮全转向电动叉车转向研究

邵新明,肖本贤

(合肥工业大学 电气与自动化工程学院,安徽 合肥 230009)

文章以叉车二自由度线性模型为基础,结合叉车自身特点与转向要求,采用横摆角速度反馈控制策略对三轮全转向叉车进行控制研究。系统仿真输入为方向盘转角,系统输出为横摆角速度和质心侧偏角,通过横摆角速度反馈形成闭环控制,从而调节3个车轮输入转角。仿真结果表明,基于横摆角速度反馈的控制策略有效改善了三轮叉车的机动性能,提高了叉车操纵稳定性。

叉车;三轮全转向;横摆角速度反馈;仿真分析

叉车作为一种工业搬运车辆,被广泛应用于工厂车间、货场、港口、车站、仓库、机场、流通中心和配送中心等场所[1],具有货物沉重,工作场地较小,转向频繁的特点。叉车本身自重较大,且负载变化较大,若转向时车速过快,则侧向力的作用易失去行驶稳定性,此时易发生侧滑或侧翻事故；但是若速度下降得过低,则不利于运输的经济性。因此叉车对转向特性的要求较高,不仅转向轻快灵活、转弯半径小,而且机动性能好。

传统的三轮叉车都是后轮机械转向,无法主动控制前轮。三轮线控转向(steering-by-wire,SBW)系统取消了转向盘和转向轮之间的机械连接,通过导线传递控制信号,实现三轮全转向。

本文在车辆二自由度线性模型的基础上,同时满足阿克曼转向定理,根据TFC20全向前移式电动叉车建立了三轮全转向叉车转向模型[2],旨在改善电动叉车的操纵稳定性和轻便性,主要研究内容包括:对TFC20全向前移式电动叉车进行数学建模,并运用Matlab/Simulink仿真软件对系统进行仿真分析;提出了基于横摆角速度反馈的三轮转向控制策略,并与不加控制算法三轮全转向控制策略和传统后轮转向控制策略作仿真比较,验证了基于横摆角速度反馈的三轮转向控制策略的优越性。

1 叉车转向系统建模

1.1 整车介绍

本文以TFC20全向前移式电动叉车为实例,对该叉车进行理论分析时,先忽略系统中的非线性部分,对其结构进行合理简化,对电动叉车整体进行数学建模,并给出转向电机的动力学模型[3]。TFC20全向前移式电动叉车主要参数如下:车身长度A为2.591 m,车身宽B为2.534 m,闭合高度H为2.8 m,前轴距为1.88 m,轴距L为1.92 m,叉车自重m为5 000 kg,转动惯量I为11 000 kg·m2,该叉车使用的是实心轮胎,其前轮侧偏刚度C1为82 618 N/rad,后轮侧偏刚度C2为153 840 N/rad。

1.2 三轮全转向二自由度整车模型的建立

在叉车转向系统中,通常车辆的运动由车辆坐标系来描述,以车辆的质心O为坐标原点,以水平面上过原点的车辆前进方向为x轴正向,以水平面上过原点的平行于驾驶员左侧的方向为y轴正向,以垂直水平面过原点的竖直向下方向为z轴正向。与叉车操纵稳定性相关的运动参量主要是质心侧偏角β、横摆角速度γ,即车身绕z轴的角速度;三轮全转向二自由度叉车模型如图1所示。

图1 三轮全转向二自由度叉车模型

图1中,O′为叉车转向中心;α1、α2、α3为三轮侧偏角;δ1、δ2、δ3为三轮转角;a、b、c为质心距前轴、后轴距离、前轮轴距;x1、x2分别为O′到后轮和x轴的距离;β为车辆质心侧偏角;γ为横摆角速度;u为叉车的速度;I为整车z轴的转动惯量;v为侧向速度。

为了满足阿克曼定理[4],转向中心交于O′,3个轮子转角必须符合如下关系:

(1)

设方向盘给定转角为θ,后轮转角δ3与方向盘给定转角θ成k的比例关系,并且方向相反。因为车轮转角通常都比较小,所以可以近似取为tanδ≈δ。根据阿克曼定理推导得到3个轮子转向角如下:

(2)

根据牛顿第二定律,由图1可以得到车辆沿y轴的力平衡方程和在xy平面的横摆运动的力矩平衡方程,其中质心侧偏角β可由公式tanβ=v/u来定义,可近似取值v=βu,即通常所指的线性二自由度模型的动力学方程式[5]为:

(3)

其中,Fy1、Fy2、Fy3为三轮的侧偏力。因为前后车轮转角δi(i=1,2,3)都比较小,所以可近似取cosδi=1,因此(3)式可以表示为:

(4)

考虑对轮胎建模时,为避免轮胎非线性特性给模型所带来的巨大影响,此处三轮全转向电动叉车使用的轮胎模型均保持在线性范围内。此轮胎模型表示为:

Fyi=-Cαiαi,i=1,2,3

(5)

当车辆质心产生离心力,前后轮引起侧向反作用力,从而引起相应的侧偏角αi(i=1,2,3),根据车辆几何关系,当轮胎侧偏角和车轮转角均较小时,根据运动学方程,则前、后轮侧偏角可以表示为:

(6)

将(5)式、(6)式分别代入(4)式中,可得二自由度三输入的状态空间方程为:

(7)

1.3 转向电机动力学模型

转向电机采用直流电动机,其等效结构如图2所示。图2中,ua2为电机电枢电压;ia2为电流;R2为电枢电阻;L2为电感。

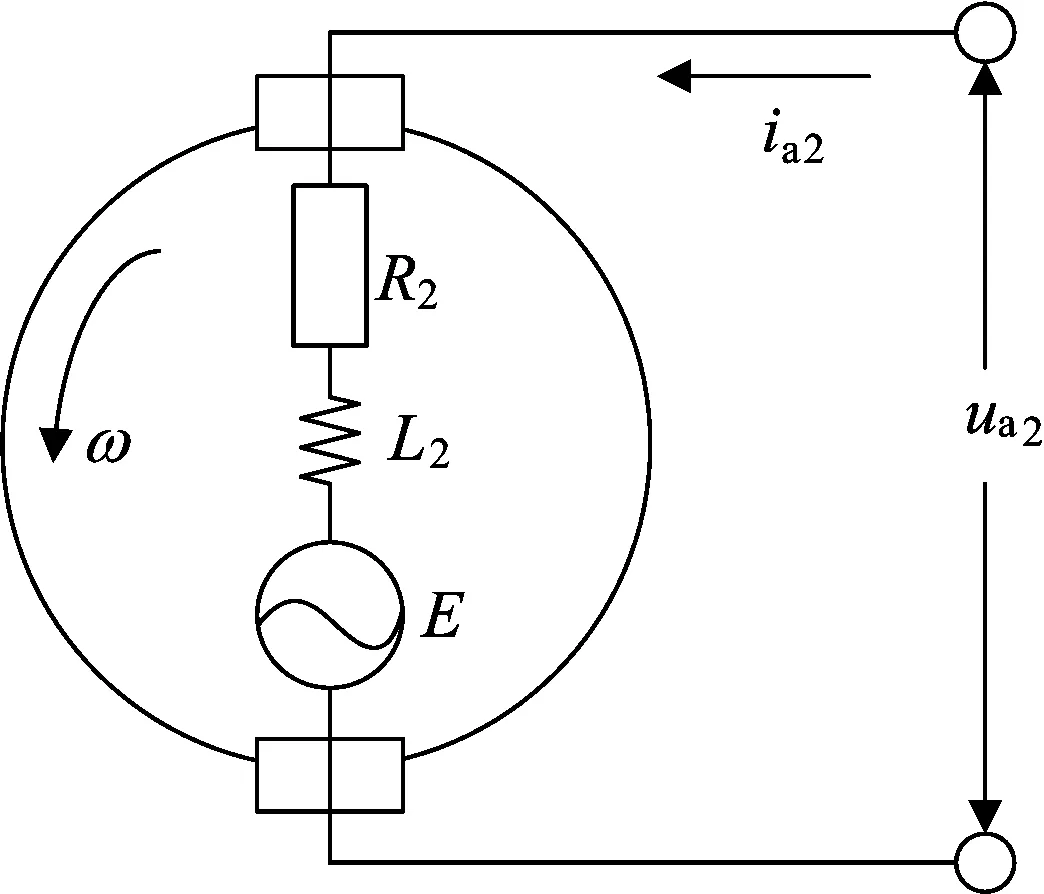
图2 直流转向电机的等效模型

由电机机械特性有:

(8)

由克希霍夫定律有:

(9)

电磁转矩方程为:

kt2ia=Tm2

(10)

消除中间变量Tm2、ia2,可得:

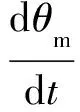
(11)

其中,ke2为反电动势系数;kt2为电磁转矩系数;mc为负载转矩。

考虑到一般情况,电枢电感L2很小,可忽略不计,则(11)式可化为线性微分方程。为求θm与ua之间的关系,可以令mc=0,即可得到动态方程如下:

(12)

由拉普拉斯变换得:

Tmθm(s)s2+θm(s)s=Kmua2(s)

(13)

其中

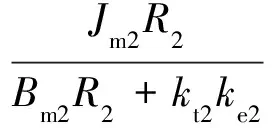
2 控制策略

叉车稳定性控制分为如下两大类问题[6]:① 轨迹保持问题,轨迹问题可由质心侧偏角来描述;② 稳定性问题,即横摆角速度问题,它与轨迹保持问题是相互联系的。

当后轮侧向力饱和达到附着极限时,将产生车辆的“激转”现象,此时转弯半径比驾驶员期望的要小,车子产生较大的横摆角速度和质心侧偏角,驾驶员将很难控制车辆。

由此可见,横摆角速度和质心侧偏角是衡量车辆操纵稳定性的重要因素[7]。下面将对车辆的横摆角速度和质心侧偏角与操纵稳定性之间的关系进行深入地分析与研究。横摆角速度反馈控制原理图如图3所示。

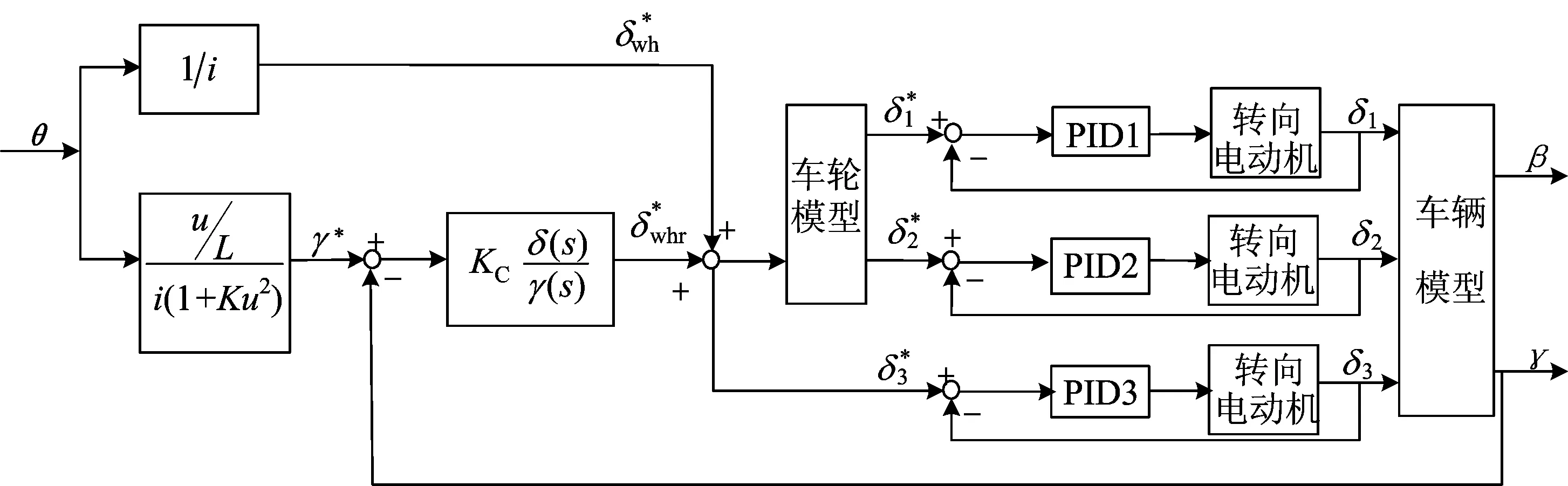
图3 横摆角速度反馈控制原理图

本文提出基于横摆角速度反馈控制的动态校正控制策略,该策略将叉车行驶时的实际横摆角速度反馈给系统,消除实际横摆角速度与理想横摆角速度之间的差值,主动校正叉车的运动状态,当叉车有失稳趋势时,使其恢复稳定性[8]。

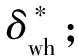
3 仿 真

为了验证横摆角速度反馈三轮转向控制策略的有效性,基于Matlab/Simulink平台进行了仿真[9]。本文根据TFC20全向前移式电动叉车的实际数据进行计算和分析,并与不加控制算法三轮转向和传统后轮转向控制策略的仿真结果进行比较,分析叉车转向时的横摆角速度响应曲线和质心侧偏角响应曲线。

3.1 空载情况下叉车转向

首先仿真叉车在空载情况下,车速选择为中速10 km/h,方向盘转角输入初始值为 0,斜率为 0.2 rad/s,经过1 s 后达到 0.2 rad,然后保持不变。调节PID控制器参数,当其参数设置为KP=20,KI=150,KD=0.09时,转向电机稳定工作。仿真得到的中速转向时质心侧偏角、横摆角速度响应曲线如图4所示。

从图4 a可以看出,横摆角速度反馈三轮转向叉车的质心侧偏角明显要比其他2种控制策略小,大约经过1.5 s后保持在-0.008 rad;不加控制算法的质心侧偏角最终保持在-0.012 rad,但其响应速度缓慢,大约要经过8 s才能达到稳定值;而传统后轮转向的响应速度虽然很快,但是其质心侧偏角过大,稳定时达到-0.033 rad,对叉车的操纵稳定性有较大影响。

从图4b可以看出,基于横摆角速度反馈控制策略的横摆角速度相对另外2种控制策略而言,其大小适中,大约经过1.5 s后保持在0.22 rad/s;不加控制三轮转向的横摆角速度响应缓慢,并且其稳定值保持在0.32 rad/s,在相同的操作条件下,其更容易产生“激转”现象,会对叉车的操纵稳定性造成不良影响;传统后轮转向的横摆角速度稳定值只有0.09 rad/s,又过于偏小,叉车的操作灵活性较差。

图4 中速转向时质心侧偏角、横摆角速度响应曲线

为了验证叉车在不同工况下的操纵稳定性,再进行1次高速情况下的仿真实验,叉车的速度为20 km/h,方向盘输入转角和PID 控制器参数保持不变。仿真得到的高速转向时质心侧偏角、横摆角速度响应曲线如图5所示。

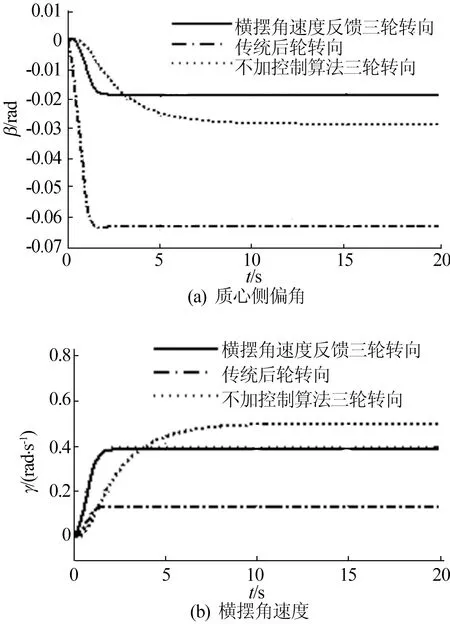
图5 高速转向时质心侧偏角、横摆角速度响应曲线

从图5a可以看出,传统后轮转向质心侧偏角最大,在1.5 s时趋向于稳定达到-0.062 rad;不加控制算法三轮转向的质心侧偏角最终保持在-0.028 rad,但其响应速度缓慢,大约要经过8 s才能达到稳定值;横摆角速度反馈三轮转向的质心侧偏角最小,稳定在-0.018 rad左右,且响应比较迅速,在3种转向策略中最稳定,总体来说所有策略质心侧偏角都比低速工况时要大。

从图5b可以看出,传统后轮转向横摆角速度上升到0.15 rad/s,但是其质心侧偏角明显过大,转向时操纵稳定性差;不加控制算法三轮转向横摆角速度最大,且响应速度过于缓慢,在经历8 s后达到稳定值0.5 rad/s,不满足叉车实际工作要求;横摆角速度反馈三轮转向横摆角速度上升到0.4 rad/s,相比于低速转向时有所上升,符合实际情况。

3.2 负载情况下叉车转向

因为实际工作中,叉车大多情况下是负载行驶的,所以选择对在额定负载情况下的叉车转向进行进一步分析[10]。负载情况下叉车的质心较空载时将发生偏移,质心计算公式如下:

(14)

其中,a为空载时叉车质心到前轴的距离;aL为货物到前轴的距离;a′为额定负载时质心到前轴的距离；G0为整车自重;GL为额定货物重;G′为额定负载时叉车总重。

本文中叉车额定负载质量GL=2 000 kg,结合(14)式,可以计算得到叉车额定负载时质心到前轴的距离为1.25 m。此时,方向盘转角同样给定输入初始值为 0,斜率为 0.2 rad/s,经过 1 s 后达到 0.2 rad,然后保持不变,车速选择中速为10 km/h。在上述情况下,对3种控制策略的叉车进行仿真比较,结果如图6所示。

从图6a可以看出,叉车在额定负载时传统后轮转向质心侧偏角最大,稳定时为-0.025 rad/s,比车在空载时有所减小;不加控制算法三轮转向质心侧偏角和横摆角速度反馈三轮转向时比较接近,最终稳定时为-0.014 rad/s,而横摆角速度反馈三轮转向质心侧偏角下降到-0.012 rad/s,同时负载对质心侧偏角达到稳定的时间影响也不大,说明叉车在负载情况下转向更稳定。

从图6b可以看出,传统后轮转向的横摆角速度稳定值为0.08 rad/s,不加控制算法三轮转向的横摆角速度稳定值为0.3 rad/s,横摆角速度反馈三轮转向的横摆角速度减小为0.2 rad/s。从而可以看出,在相同行驶速度下,叉车额定负载时的横摆角速度比叉车空载时的横摆角速度变化不大,即保持良好的转向稳定性。

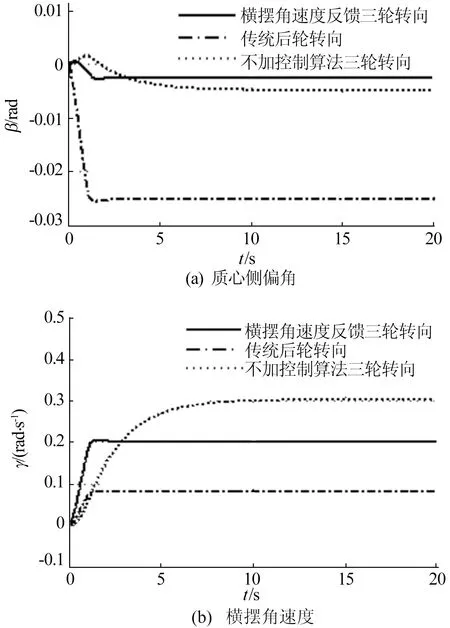
图6 额定负载情况下质心侧偏角、横摆角速度响应曲线

综上所述,通过比较叉车在空载和额定负载时3种控制方法的仿真结果可以看出,基于横摆角速度反馈控制下叉车稳定时的横摆角速度大小适中,且叉车的质心侧偏角最小,叉车的操作稳定性能最好;在相同的操作下,不加控制算法三轮转向的横摆角速度过大,传统后轮转向控制方法下的横摆角速度过小,并且它的质心侧偏角也是最大的,从而导致这2种方法都不能满足叉车的作业要求。因此,通过分析比较3种控制策略下的仿真结果,明显可以看出,基于横摆角速度反馈控制策略下的三轮转向叉车的操纵稳定性能最好。

4 结 论

本文通过对二自由度整车模型下三轮全转向叉车转向系统转向性能的研究,提出了基于车速、车轮转角的横摆角速度反馈的三轮转向控制、传统后轮转向控制和不加控制算法三轮转向控制3种控制策略。仿真结果表明,传统后轮转向控制下叉车的横摆角速度过小,质心侧偏角过大,从而导致叉车的转弯半径过大,且操纵稳定性较差。不加控制算法三轮全转向控制下叉车的横摆角速度过大,容易出现甩尾现象。相比于另外2种控制策略,基于横摆角速度反馈的三轮转向控制策略在保证叉车具有良好的操纵稳定性的同时,又实现了灵活转向,满足了叉车在现实工作中的作业要求,进一步降低了驾驶员的操作负担和紧张程度。

[1] 舒利盛,王璐伟,李国平.电动物料搬运车动力转向技术的发展现状[J].车辆与动力技术,2014(4):57-61.

[2] 姚江云,孔峰,吴方圆.线控转向汽车传动比智能控制策略的研究[J].计算机测量与控制,2012,20(3):678-680.

[3] 吴信丽,章文誉,葛立银,等.叉车转向机构优化设计[J].工程机械,2014,45(7):51-52.

[4] ACKERMAN J,ODENTHAL D,BUNTE T.Advantages of active steering for vehicle dynamics control[C]//Proceedings of 32nd ISATA,Automotive Mechatronics Design and Engineering.[S.l.:s.n.],1999:263-270.

[5] 王晨.基于MATLAB四轮转向车辆PID控制的建模与仿真[J].成都大学学报(自然科学版),2015,34(4):405-407.

[6] SILVA A, NEVES A,COSTA E.SAPPO:a simple,adaptable,predator prey optimises[C]//11th Portuguese Conference on Artificial Intelligence,EPIA 2003,Heidelberg:Spring-Verlag,2003:59-73.

[7] 刘奕敏,黄国建,谢小鹏.前移式叉车转向稳定性分析[J].自动化与信息工程,2014,35(6):23-26.

[8] 宗长富,郑宏宇,田承伟,等.基于理想传动比的汽车线控转向控制算法[J].汽车工程,2007,29(8):1230-1235.

[9] 刘春辉,王增才.四轮转向车辆操纵稳定性仿真分析[J].计算机仿真,2008,25(8):253-256.

[10] 林程,孟祥,陈思忠,等.四轮转向车辆转向特性分析及试验研究[J].北京理工大学学报,2004,24(3):218-221.

Researchonthree-wheelsteeringofelectricforkliftbasedonyawratefeedback

SHAO Xinming,XIAO Benxian

(School of Electric Engineering and Automation, Hefei University of Technology, Hefei 230009, China)

Based on two-degree-of-freedom(2-DOF) linear model, and considering the features of forklift and its steering requirements, the three-wheel steering forklift was controlled by adopting yaw rate feedback control strategy. The steering wheel angle was input to the simulation of vehicle system and the output of the system was the yaw rate and sideslip angle, and the closed-loop control was formed by yaw rate feedback to adjust the input angle of three wheels. The simulation result shows that the control strategy based on yaw rate feedback can effectively improve the flexibility and handling stability of the forklift.

forklift; three-wheel steering; yaw rate feedback; simulation analysis

2016-03-15；

2016-05-31

国家自然科学基金资助项目(61304007)

邵新明(1989-),男,河南信阳人,合肥工业大学硕士生;

肖本贤(1964-),男,安徽无为人,博士,合肥工业大学教授,硕士生导师.

10.3969/j.issn.1003-5060.2017.11.012

U463.42

A

1003-5060(2017)11-1496-06

(责任编辑 张 镅)