内斜微线段齿轮数字化制造理论研究
赵 韩,高 峰,刘 鹏
(合肥工业大学 机械工程学院,安徽 合肥 230009)
内斜微线段齿轮数字化制造理论研究
赵 韩,高 峰,刘 鹏
(合肥工业大学 机械工程学院,安徽 合肥 230009)
微线段齿轮是一种新型齿轮,具有承载高、效率高、寿命长等特点。为弥补对内斜微线段齿轮研究理论和加工方法的不足,文章借鉴范成法加工齿轮的思想,利用微线段齿条法面齿廓方程,通过坐标变换方法推导了内斜微线段齿轮的通用齿面方程,并证明了齿面的光滑连续性;针对上述齿面方程,通过编写计算机程序实现了基本齿廓的绘制,并导入三维绘图软件中完成三维模型的创建;利用线切割方法加工出齿轮样件,并与三维模型进行对比,结果表明线性插补法获得内斜微线段齿廓的方法可行。该研究为内斜微线段齿轮应用于高精度传动系统等相关产品的设计和制造提供了一定的理论参考和应用基础。
内斜微线段齿轮;齿面方程;线性插补;电化学加工
内斜齿轮传动具有承载能力大、结构紧凑、啮合平稳、冲击噪声小等优点[1-2],广泛应用于汽车、船舶、矿山机械、风力发电机械等设备中[3-4],并具有举足轻重的地位。然而,随着科学技术的进步,传统的渐开线内斜齿传动已不能满足人们对其强度、体积、效率等方面的要求。微线段齿轮是一种新齿廓齿轮,是一种不同于传统渐开线齿轮的全新啮合齿轮。研究表明,微线段齿轮具有较高的弯曲强度及接触强度,最少齿数较少(3~4齿),啮合效率高。而内斜微线段齿轮则可以兼备内斜齿轮和微线段齿轮的优点,能很好地适应现代工业对齿轮传动性能全方位的要求,尤其是在高速、重载和小型化方面将会有很好的运用,具有广阔的应用前景。
20世纪80年代末,文献[5]首次提出了微线段齿轮,其齿形由许多微段渐开线连接而成,与传统渐开线齿轮相比,微线段齿轮的承载能力和耐磨性显著提高。本研究团队多年来一直从事微线段齿轮的相关研究,解决了微线段齿轮齿廓的形成原理及特性的问题[6],推导出了微线段齿轮齿廓的曲线方程和传动效率计算公式[7],建立了微线段齿轮的动态模型[8],通过相关参数的调整,优化了微线段齿轮的几何尺寸[9],分析了微线段齿轮特殊参数对其啮合刚度的影响规律[10],对比了微线段齿轮与渐开线齿轮的温升[11]及弯曲强度[12]方面的性能,也研究了斜齿微线段齿轮的胶合承载能力[13]和刚度[14]。虽然前期在微线段齿轮理论研究方面取得了一定成果,但对内斜微线段齿轮原理和制造的研究还存在不足。微线段齿轮与渐开线齿轮相比,主要区别是齿廓不同,因此本文拟借鉴渐开线内斜齿轮的加工方法制造内斜微线段齿轮。
目前,渐开线内齿轮加工主要有磨削加工、插齿加工、拉削加工、铣削加工等。文献[15]研究了采用磁性磨料磨削内齿轮,加工出了3种材料高精度的内齿轮;文献[16]根据剐齿原理,研究了内斜齿轮的剐齿加工,并设计了齿轮的剐齿刀具[17];文献[18]针对helipoid新型齿轮的加工,提出了一种新型插齿刀的设计理论;文献[19]提出了在滚齿机上用直齿插齿刀加工内斜齿轮;文献[20]研究了螺旋拉削制造汽车变速器中的内齿圈;文献[21]研究了利用高效盘形可转位齿轮铣刀加工内齿轮。这些研究工作在一定程度上弥补了现有内斜齿轮加工工艺的不足,但在一些有空间限制的场合则无法满足要求。例如汽车自动变速器行星轮系内齿轮的加工,由于内齿轮内径较小,且行星轮系结构紧凑,滚齿、铣齿、插齿都将无法实现,螺旋拉刀及紧密磨削虽然能加工内径较小的渐开线内斜齿轮,但是其价格相对很高,且由于内斜微线段齿轮的齿形较复杂,螺旋拉削及紧密磨削也很难加工。
本文在前期研究的基础上,开展内斜齿微线段齿轮的成型原理及制造的研究,为后续该种齿轮应用于高精度传动系统提供一定的理论支持和应用基础。
1 微线段齿条法面齿廓的构造
1.1 基本思想
用范成法原理加工内斜齿轮时,为便于求解,可以将其看成假想齿条和内齿轮的啮合,因此,先构造基本齿条齿廓,再利用范成原理得到内斜齿齿廓。
理论上微线段齿廓由若干段渐开线光滑连接而成,而实际加工形成的齿廓曲线或曲面必然是由很多微小的直线段或平面连接而成。由于连接点(零点)数量庞大,可通过插补原理将相邻零点直线连接来近似理论轮廓曲线。
1.2 微线段齿条法面轮廓方程
根据团队前期的研究,标准微线段齿条的法向齿廓如图1所示。详细构造过程及 (1) 式的推导参见文献[6]。

图1 微线段齿条法面齿廓的构造
对于凸齿廓上任一零点k,在图1所示坐标系O1x1y1中,其坐标方程可以描述为:
(1)
其中,rbi为与rb0有关且按选定规律变化的第i点基圆半径;δi和αi分别为:
δi=arccos[2cos(αi-1+δ)-cosαi]+(αi-1+δ)
(2)
αi=αi-1+(δ+δi)
(3)
2 通用齿面方程
2.1 法面齿条上任意零点的法矢
由(1)式求出的仅是离散点的坐标,为求接触点的法矢进而得到齿面方程。
设理论轮廓曲线为f(x),因为零点数目庞大,一个齿廓上就有几万乃至几十万个,相邻两零点间的距离很短,所以可以认为,对于任意零点处有xk+1-xk→0,则有:
(4)
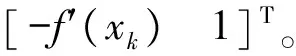
2.2 由法向齿形求基本齿条齿形
为了导出基准齿条齿面方程式,建立2个坐标系,如图2所示。图2中,σ(t)为端面坐标系,O(t)x(t)y(t)与基本齿条的一个端面重合;σ(n)为法面坐标系,O(n)x(n)y(n)与基本齿条法面重合,且与σ(t)平面的坐标原点重合,相当于图1中的O1x1y1坐标系。
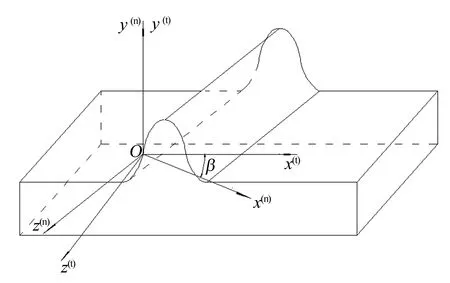
图2 基本齿条的端面与法面坐标系
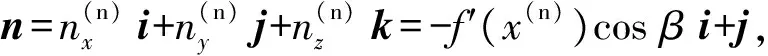
(5)
(6)
2.3 通用齿面方程的求解
由范成加工原理可知,微线段齿轮的齿面是基本齿条齿面的包络面,为方便求解,建立的3个坐标系如图3所示。
图3中,σ(0)为空间固定坐标系,O(0)x(0)z(0)平面与齿条节平面重合;σ(1)为与齿条固连的坐标系,O(1)x(1)y(1)平面与齿条的一个端面重合,与齿条节平面重合,且在起始位置时,σ(1)与σ(0)重合,此处的σ(1)相当于图2中σ(t);σ(2)为与内斜齿轮固连的坐标系,O(2)点位于齿轮的转动轴线上,O(2)x(2)y(2)平面与齿条的一个端面重合,且在起始位置时,y(2)轴与y(0)轴重合。
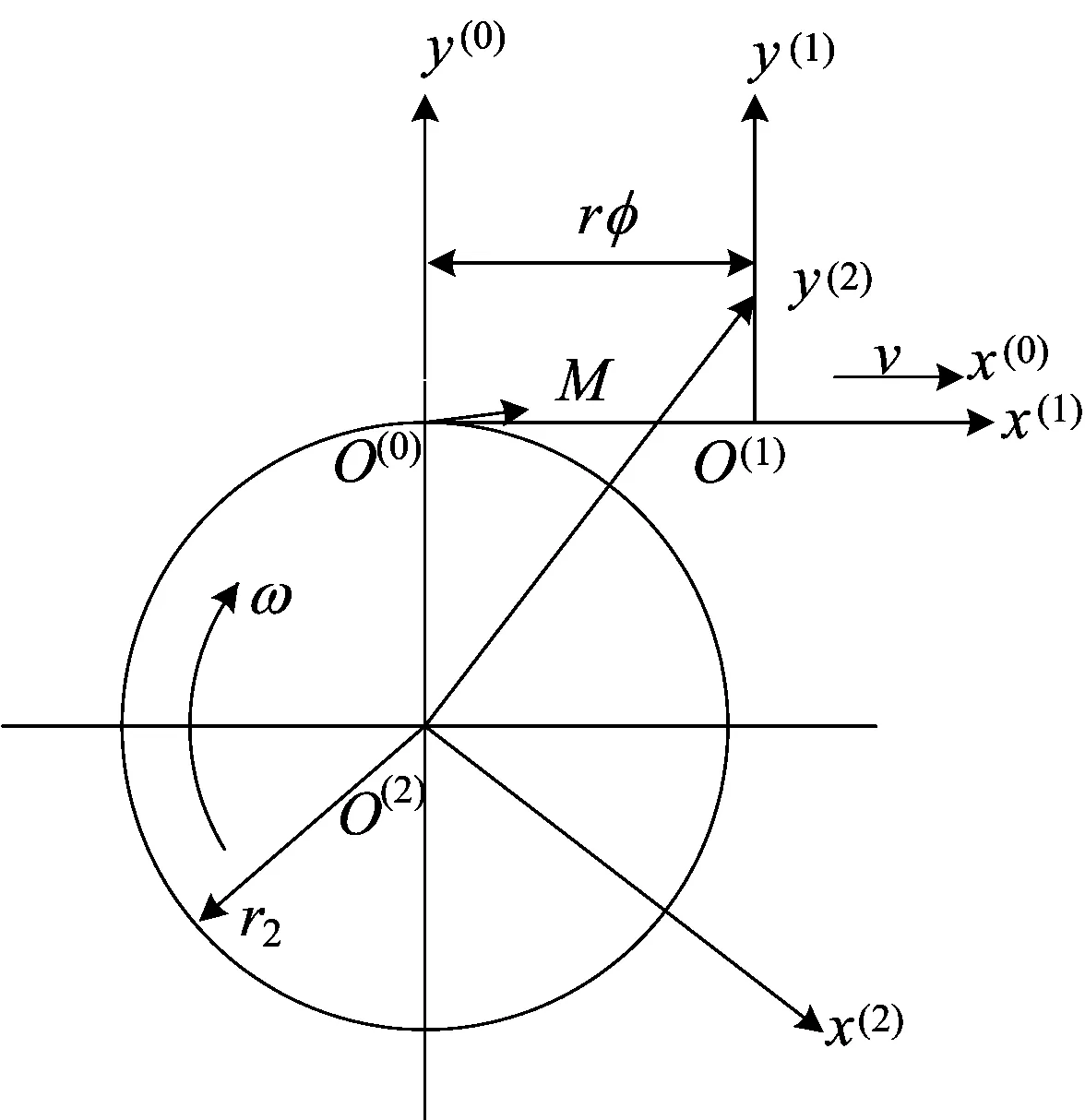
图3 求解齿面方程所用的坐标系
设齿条移动速度大小为v,即v(1)=vi;齿轮的移动速度大小为ω,即ω(2)=ωk;齿轮的节圆半径为r2。当齿条的移动距离为ωr2时,齿轮转过的角度为φ,此时齿廓上的M点成为接触点,则有:
v=ωr2
(7)
M点随齿条的移动速度为:
(8)
M点随齿轮运动的速度为:


(9)
(8)式与(9)式相减,并将(7)式代入得到齿轮齿条在M点的相对运动速度为:
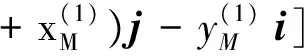
(10)
将(6)式和(10)代入啮合方程式n·v(12)=0得:

(11)
将(5)式代入(11)式得:

(12)
坐标系σ(1)与σ(2)间的坐标变换式为:
(13)
再将(5)式代入(13)式即可得到齿轮的齿廓方程,即
(14)
3 理论齿面的光滑连续性验证
图1中,在法面轮廓上,公共发生线giSi在半径均为rbi的相切基圆Oi、Oi′上生成的微小渐开线miSi、mi-1Si在Si点处有相同的曲率中心(基圆Oi、Oi′的切点),因此轮廓在Si点处是光滑连续的;微小渐开线miSi在零点mi处的曲率中心为基圆Oi′与节线的交点ni,由法面轮廓的构造过程可知,ni同时又是基圆Oi+1与节线的交点,因此ni也是miSi+1在mi处的曲率中心,轮廓在零点mi处是光滑连续的,即法面齿廓是由若干微小渐开线光滑连接而成。
设KK′是一条垂直于法面方向的直线段,当法面轮廓上每生成一个微小渐开线时,KK′上连续的每个点同时生成了一个微小渐开线,因此该直线段生成了一个光滑连续的微小渐开面,则内斜微线段齿轮在垂直于法面方向也是光滑连续的。根据共轭原理,最终形成的内斜齿微线段齿轮在整个齿面上均是光滑连续的。
根据上述原理及公式,本文编制了微线段齿轮生成程序,开发了一套微线段齿轮生成软件。借助该软件获得的内斜微线段齿轮如图4所示。

图4 软件生成的斜齿微线段齿轮
4 内斜微线段齿轮加工
4.1 加工原理
每条齿廓上包含上万甚至几十万个零点,十分密集。为便于加工,在实际中通常采用相邻零点直线段连接的方式,即用微线段代替原来的微小渐开线来近似理论齿面。由上文分析可知,曲线mi-1mi由微小渐开线mi-1Si和miSi光滑连接而成。显然相邻零点直线连接时,得到的近似齿面仍然是连续的,且由于微小渐开线很短,一般在微米以下,因此完全可以用微线段代替。
根据线性插补原理,在各零点坐标已知的情况下,对于由若干离散零点线性连接构成的齿面轮廓,可以由线性插补得到。因此由(14)式给出的内斜微线段齿轮齿面离散点坐标,可以通过电化学加工获得内斜微线段齿轮。
4.2 样件制造
4.2.1 参数设计
本次加工的内斜微线段齿轮样件,旋向为左旋,其基本参数见表1所列。

表1 内斜微线段齿轮基本参数
4.2.2 样件加工
本文样件的加工基于文中公式及插补原理,进而得到内斜微线段齿轮的齿廓,采用数字仿形原理,利用编写的程序,在通用的加工中心上实现内斜微线段齿轮样件的加工。线切割数控加工内斜微线段齿轮实验平台如图5所示,线切割数控加工得到的内斜微线段齿轮如图6所示。
通过三维模型和加工实物的对比,证明了线性插补法获得近似理论内斜微线段齿廓的可行性,也验证了本文公式及编写的内斜微线段齿轮生成程序的正确性。

图5 线切割数控加工内斜微线段齿轮实验台

图6 电化学数控加工得到的内斜微线段齿轮
5 结 论
(1) 本文在前期研究的基础上,将范成法加工内斜齿轮的过程看成假想齿条与内斜齿轮的啮合过程,导出了内斜微线段齿轮的通用齿面方程,证明了范成法加工内斜微线段齿轮的可行性。
(2) 通过分析理论微线段齿条齿面的光滑连续性,编写计算机程序绘制内斜微线段齿轮的基本齿廓,证明了内斜微线段齿轮齿面的光滑连续性。
(3) 采用电化学方法加工内斜微线段齿样件,通过样件与三维模型的对比,得出了线性插补法获得近似理论内斜微线段齿廓的可行性。该研究对内斜微线段齿轮的设计制造有一定的参考意义,也为该种齿轮应用于高精度传动系统等相关产品的设计和制造提供了新的理论参考和应用基础。
[1] 王世宇,宋轶民,张策,等.行星齿轮传动的基本参数对动态特性的影响[J].中国机械工程,2005,16(7):615-617.
[2] 任小中,邓效忠,苏建新,等.内齿轮成形磨削及砂轮修形技术的研究[J].中国机械工程,2008,19(22):2647-2649.

[4] QIU X,HAN Q,CHU F.Load-sharing characteristics of planetary gear transmission in horizontal axis wind turbines[J].Mechanism and Machine Theory,2015,92:391-406.
[5] KOMORI T,ARIGA R,NAGATA S.A new gear profile having zero relative curvature at many contact points(Logix tooth profile)[C]//Proceeding of International Power Transmission and Gearing conference.[S.l.]:ASME,1989:599-606.
[6] 赵韩,梁锦华,刘红雨,等.微线段齿廓的形成原理及特性[J].机械工程学报,1997,33(5):7-11.
[7] 黄康,赵韩,田杰.微线段齿轮与渐开线齿轮温升对比实验研究[J].中国机械工程,2006,17(18):1880-1883.
[8] 黄康,赵韩.微线段齿轮与渐开线齿轮的弯曲强度比较分析[J].农业机械学报,2001,32(1):115-117.
[9] 黄康,田杰,赵韩,等.斜齿微线段齿轮胶合承载能力的研究[J].合肥工业大学学报(自然科学版),2005,28(2):118-120,124.
[10] 黄康,赵韩,赵小勇.斜齿微线段齿轮刚度研究[J].农业机械学报,2005,36(4):119-122.
[11] 陈奇,赵韩,黄康.微线段齿轮传动效率的计算理论研究[J].中国机械工程,2011,22(13):1537-1539.
[12] XIONG Y,HUANG K,WANG T,et al.Dynamic modelling and analysis of the microsegment gear[J].Shock and Vibration,2015,501:697857.
[13] 刘鹏,赵韩,黄康,等.微线段齿轮啮合刚度及其参数影响规律研究[J].机械传动,2015,39(4):11-14.
[14] 刘红雨,赵韩,梁锦华.微线段齿轮的齿廓参数选择及几何尺寸的计算[J].机械传动,2001,25(4):27-28.
[15] WANG Y,HU D.Study on the inner surface finishing of tubing by magnetic abrasive finishing[J].International Journal of Machine Tools and Manufacture,2005,45(1):43-49.
[16] 李佳,陈新春,张鸿源.圆柱齿轮剐齿技术[J].机械工程学报,2011,47(19):193-198.
[17] 李佳,娄本超,陈新春.基于自由曲面的剐齿刀结构设计[J].机械工程学报,2014,50(17):157-164.
[18] 景文林.在滚齿机上用直齿插齿刀加工内斜齿轮[J].机械制造,2000,38(2):12.
[19] WU J L,LIU C C,TSAY C B,et al.Mathematical model and surface deviation of helipoid gears cut by shaper cutters[J].Journal of Mechanical Design,2003,125(2):351-355.
[20] 庄中.汽车齿轮加工的新技术和发展动向[J].汽车工艺与材料,2008(6):43-47.
[21] 陈小杰.高效盘形可转位齿轮铣刀的特点及应用[J].制造技术与机床,2008(7):159-160.
Researchondigitalmanufacturingtheoryofinternalbevelmicro-segmentgear
ZHAO Han,GAO Feng,LIU Peng
(School of Mechanical Engineering, Hefei University of Technology, Hefei 230009, China)
Micro-segment gear is a kind of special gear with characteristics of high efficiency and loading capacity, long service life, etc. To make up the lack of theory and processing method for the internal bevel micro-segment gear, and in view of the principle of machining gear by generating method, its common tooth surface equation was deduced by coordinate transforming from basic rack normal profile. The smoothness and continuity of its tooth surface was also verified. The 3D model was built via 3D drawing software based on the drawing of basic tooth profile by programming, and the model was compared with a gear sample processed by electrochemical method. The results show that linear interpolation is a feasible method to obtain the internal bevel micro-segment gear profile. This study can provide theoretical support and application foundation for the application of the internal bevel micro-segment gear in the design and manufacturing of high precision drive systems and other related products.
internal bevel micro-segment gear; tooth surface equation; linear interpolation; electrochemical machining
2016-03-24;
2016-06-03
国家国际科技合作专项基金资助项目(2014DFA80440);安徽省自然科学基金资助项目(1408085MKL12)
赵 韩(1957-),男,安徽宿州人,博士,合肥工业大学教授,博士生导师.
10.3969/j.issn.1003-5060.2017.11.001
TH132.429
A
1003-5060(2017)11-1441-05
(责任编辑 胡亚敏)

