500 kV超高压输电线下山坡周围工频电场分析*

李永明，杨骏，邹岸新，王洋洋，徐禄文，付志红

（1.重庆大学输配电装备及系统安全与新技术国家重点实验室，重庆400044；2.国网重庆市电力公司电力科学研究院，重庆401123）

0 引 言

近年来随着我国电压等级不断升高，输电容量不断增大，在输电工程中电磁环境问题成为输电线路架设的重点考虑对象。在输电线路架设中会遇到各种复杂的情况，比如在山地，丘陵等地架设时，其不平的地形会对电场的分布产生影响，从而会影响对按平坦地面标准架设的输电线路的电磁环境的评估。针对这方面的研究，国内外已有了相关的研究，然而其不平坦地形的电场计算研究主要针对的是二维模型。重庆大学俞集辉教授等人用优化模拟电荷法对凹凸不平的地面，运用优化算法，寻找模拟电荷的最优布点位置来减小计算量［1］。东北林业大学周宏威等人运用模拟电荷法和镜像法相结合后的改进的格林函数法，对单面山坡的电场分布进行了计算研究［2-3］。还有一些研究学者运用了不同的方法，比如模拟电荷法，有限元法，边界元法等，对房屋周围的电场分布情况进行了三维模型的建立及仿真计算［4-7］。在一些相关研究中都将地面视为平坦的，并运用镜像法与模拟电荷法进行电场的分布计算［8-10］，还有一些关于输电线三维电场的研究则是基于有限元电磁场计算软件，对房屋周围的电场进行计算［11-18］。在上述的文献中关于山坡附近的三维电场的研究较少，对复杂的地面也只是进行了二维的电场计算。

本文对500 kV输电线路下方不平坦地面进行三维建模，运用模拟电荷法分析山坡地形周围的电场分布，讨论其电场分布的影响因素，以便进一步为复杂地形周围的电场环境分析提供可靠依据。

1 计算方法

模拟电荷法的基本思想是在计算场域之外设置n个离散的模拟电荷来等效替代电极表面上连续分布的自由电荷以及介质分界面上连续分布的束缚电荷，依据静电场唯一性定理，依据等值替代前后边界条件不变的前提条件，来求得各模拟电荷量，从而可以将各模拟电荷所产生的场量（φ，E）叠加，求得场域内任意一点的电位和场强［7］。由于本文研究的对象是开域问题，且研究的山坡不适合用镜像法，所以本文采用模拟电荷法来进行计算研究。

本文将分裂导线等效为一根导线，其导线的等效半径计算公式参考文献［7］可得，导线视为水平排列的直线，将导线剖分为间断的点，用点电荷代替，模拟电荷布置在导线圆心处，地面与山坡表面分别剖分为不同大小的网格。将各个网格的节点，设为匹配点，在两个匹配点的中点设为校验点，在地表面内部，垂直匹配点位置一定距离内设置模拟点电荷，由此可得求解场域内任意一点P处的电位φp，其示意图如图1所示。

式中qi，qj分别为输电线和地面上的模拟电荷；Ri，Rj分别为各个模拟电荷到P点的距离。模拟电荷到场域中任意一点的距离Rk为：

图1 场域内任意一点的电位Fig.1 Potential of any pointwithin the field

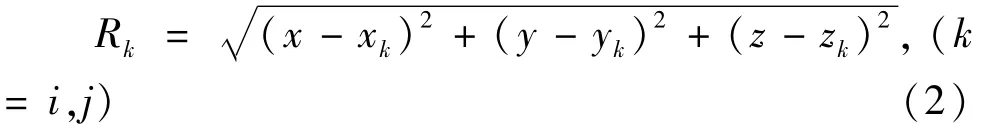
从而可得到各个匹配点的电位方程为：

其中：

式（3）中 Q为待求解的模拟点电荷；φ0为各个匹配点的电位。根据求解得到的模拟电荷Q，又由电场与电位的关系（φ为空间任意一点的电位）可得空间任意一点X，Y，Z各个方向的电场强度 Ex，Ey，Ez为：

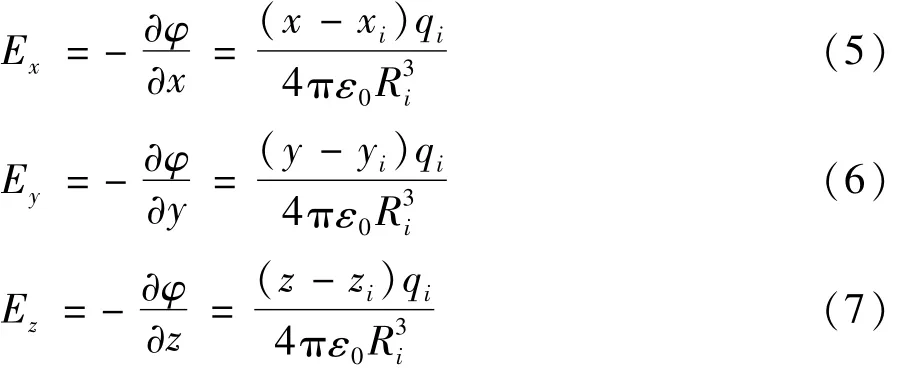
其任意一点的总的电场强度为：

2 山坡附近电场计算模型

本文以直角坐标为全局坐标，X轴方向为输电线行进方向，Y轴方向为输电线横向方向，输电线与地的纵向方向为Z轴，导线水平排列，其中B相与X轴重合，在输电线档距的中点设为坐标源点。由于实际情况比较复杂，在模型的建立时做如下的简化：

（1）山坡坡面平整，无凹凸曲面；

（2）只考虑线路下方部分，忽略金具、杆塔、绝缘子等物体的影响；

（3）将地面及山坡表面视为良导体，其表面电势为零。

简化后线路及山坡的模型的三视图如图2所示。

图2 计算模型的三视图Fig.2 Calculation model of the three view drawing

图2中A，B，C三相输电线的间距为12 m；H为输电线与地面之间的高度；h为山坡的高度；α，β分别为山坡坡脚的角度；k1，k2分别为山坡两边在Y轴的投影宽度；L为山坡沿着X方向的长度。图3为在山坡周围，x为正负20 m，y为正负40 m的区域内的模拟电荷点及匹配点的分布示意图，其在山坡断面处，斜率无限大，此处电场畸变值很大，所以此处不布置模拟电荷。

3 山坡周围工频电场的计算

3.1 验证算法

为了验证算法的正确性，首先根据模拟电荷法可知在此模型的计算中，其输电线及地面网格的剖分密度会对其计算精度产生影响，且模拟电荷点与边界面的垂直距离与其左右两边的匹配点的距离的比值f有关。其中f＝a/b，a为模拟电荷与匹配点的垂直距离，b为该处左右相邻的两个匹配点间的距离，所以先要验证布置的模拟电荷的合理性，其计算精度是否达到工程要求。

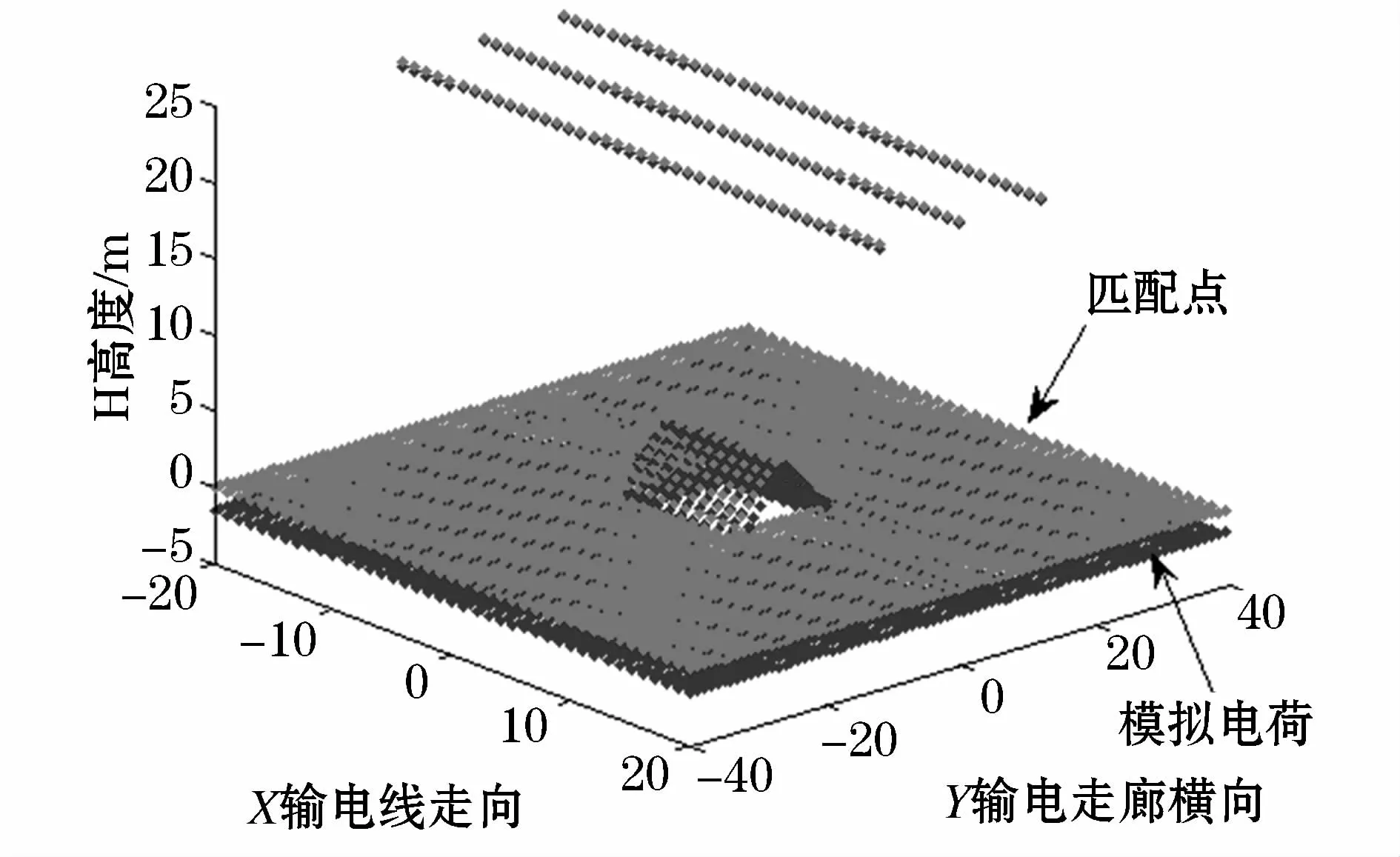
图3 模拟点与匹配点的分布Fig.3 Distribution of the simulation and matching points

本文将输电线与地面分开剖分，输电线的Y，Z坐标都为定值，所以沿X轴方向剖分，其每个剖分单元的长度为Lx。地面及山坡X轴和Y轴方向均做剖分，其沿X轴方向每个剖分单元的长度为Dx，沿Y方向每个剖分单元的长度为Dy，剖分单元的单位均为m。其根据不同的剖分方案及f取值，校验点取在输电线的每个剖分单元的中点处得到的校验点的相对误差%，计算得到的地面及山坡表面的校验点的平均电势为VJ，单位为V，如表1所示，其中N为总的剖分单元个数，其相对误差的计算公式为：

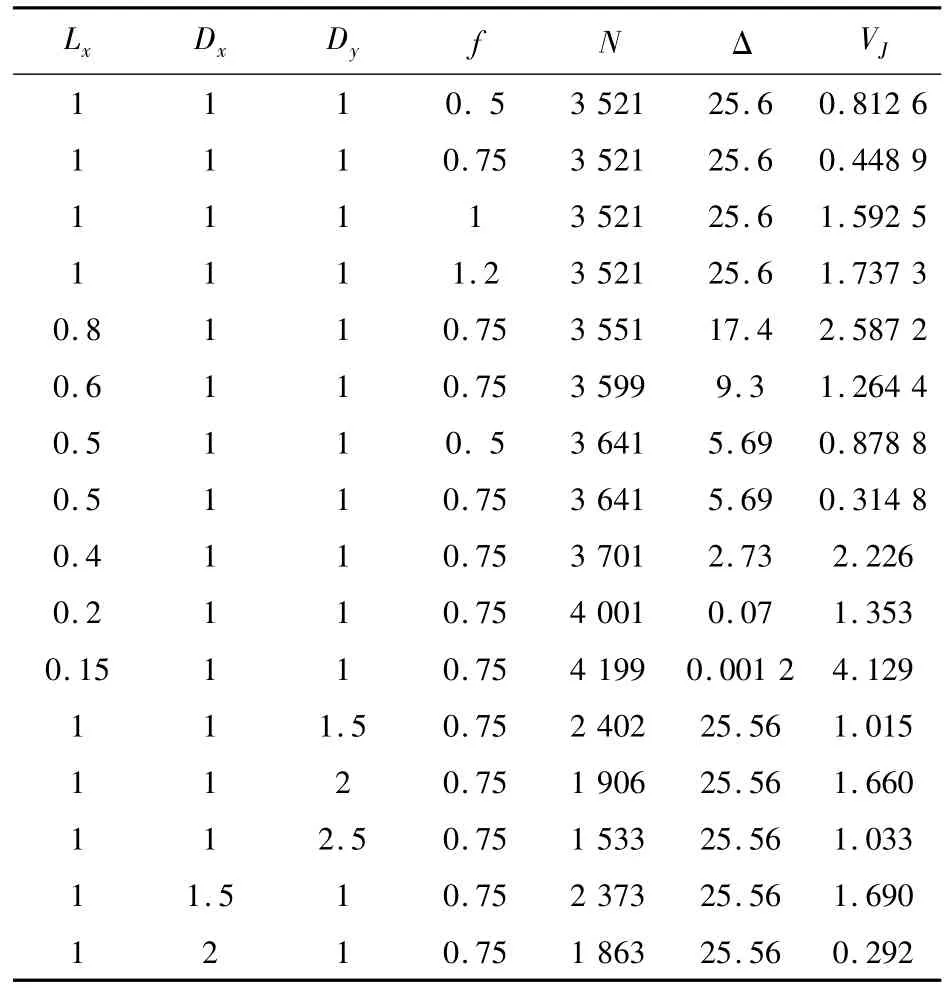
表1 剖分方案及计算结果Tab.1 Subdivision scheme and the calculation results

按表1的剖分方案，其在x＝0 m处的折线对比结果如图4所示。

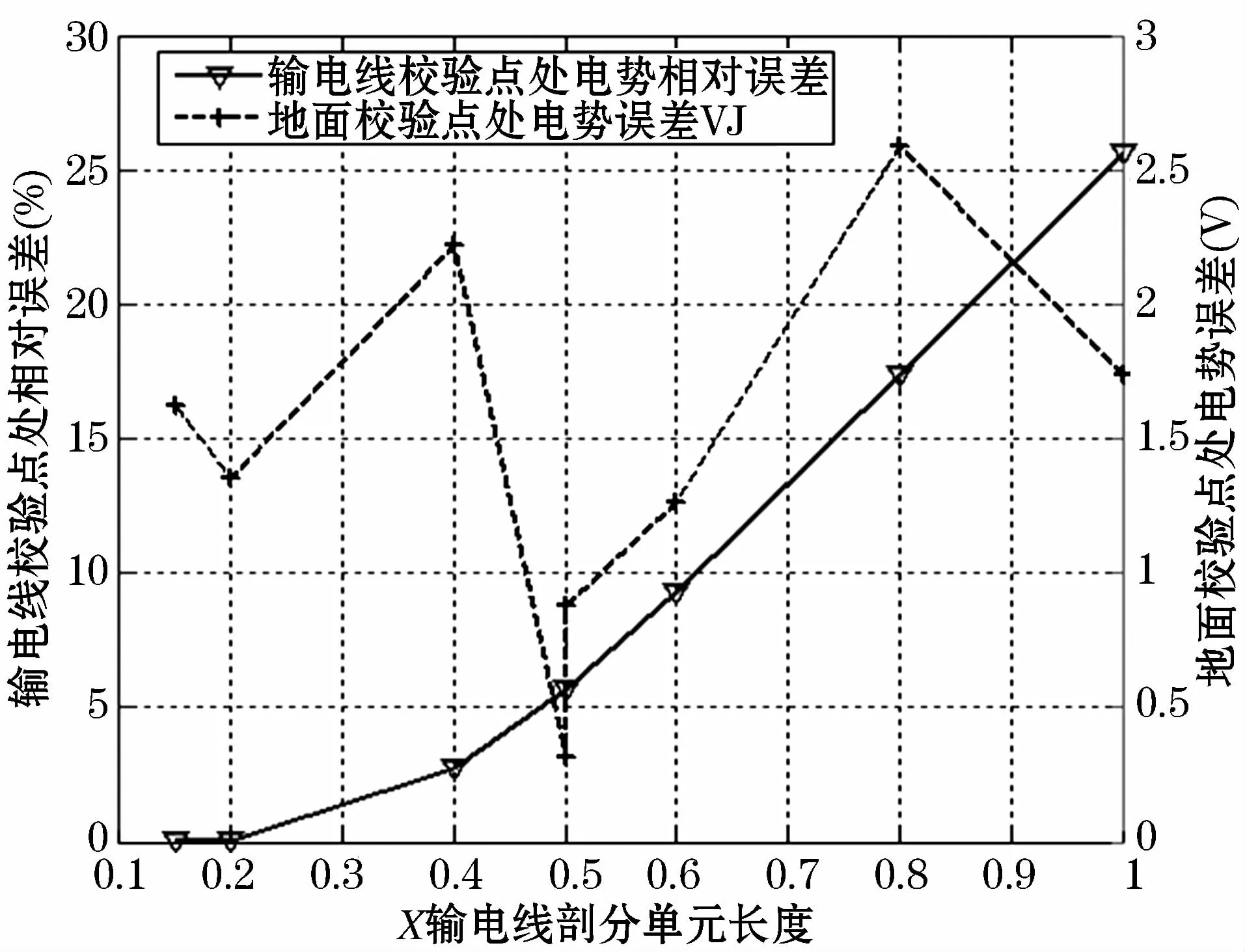
图4 不同方案剖分其校验点处电势的误差对比Fig.4 Comparison of electric potential errors of the chick points in different subdivision schemes

从图4及表1可知，其当输电线的剖分单元长度越小时，在输电线上的校验点计算等到的电势的相对误差越小，其与Lx近似成线性关系，在输电线剖分单元长度相同的情况下，改变山坡及平地上X轴方向及Y轴方向上的的剖分单元长度，对其输电线上计算得到影响可以忽略不计，而对地面及山坡表面的校验点计算得到的电势最大不超过5 V。在f取值0.75，Lx＝0.5 m时，其地面上校验的电势误差较小VJ＝0.314 8 V，，所以本文选取 Lx＝0.5 m，Dx＝1 m，Dy＝1 m，f＝0.75的剖分方案既可保证计算精度，又可降低剖分单元的个数，比较合适进行仿真计算。

本文为了进一步验证算法的正确性，将测得的测量值与在相同位置时的仿真结果进行对比，测量地点为重庆大学城陈家桥500 kV陈长I线2号塔与3号塔之间山坡地形，其中输电线的电压为500 kV，导线的悬挂高度H为24 m，各相导线之间的间距为12 m，其在x＝0m处离地1.5 m时，分别对平地的仿真值与测量值的对比，存在山坡时的仿真值与测量值的对比结果如图5所示。

由图5可知其编程仿真结果与测量的结果相符，计算方法正确。

3.2 山坡周围电场分布的计算

根据图2、图3所建立的计算模型，X轴与B相输电线在同一平面内，山坡的高度h＝5 m，山坡左右两边的起坡角度为α＝β＝30°，山坡在输电线正下方，左边坡脚位置为y＝ －5m，在x＝0m，x＝ －5.5 m，x＝－15 m处，计算其距离平地及山坡表面1.5 m区域处的电场，其电场分布曲线的对比结果如图6所示。

图5 测量值与仿真值对比结果Fig.5 Contrast result of themeasured value and the simulate value

图6 x＝0 m、x＝－5.5 m及x＝－15 m处电场对比结果Fig.6 Contrast results of the electric field in x＝0 m，x＝－5.5 m and x＝－15 m

由图6可知，x＝0 m处为沿着Y轴方向电场分布在山坡两边的山坡坡脚位置附近，电场在接近坡脚时，电场强度先减小，随着山坡逐渐增强，到达山坡顶点处电场强度最大约为5.7 kV/m，然后随着山坡右侧的山坡，高度的降低，电场强度逐渐减小，在右侧坡脚位置，电场由一个逐渐下降的趋势变为电场上升的趋势。在x＝－5.5 m处，其截面与山坡的断面接近，从其电场的分布曲线可以看出，在接近山坡断面出的电场，在坡脚位置，电场发生畸变，其畸变值约与山坡顶点处的场强值相当，都超过了5 kV/m，然后电场的变化与平地时的变化趋势相同。在x＝－15 m处的电场变化趋势，与无山坡时，在相同位置处的电场变化情况相似，其原因是在x＝－15 m处时，已离山坡较远，山坡对其x＝－15 m处的电场影响较小。

由此可知在远离山坡的截面处，山坡对输电线下的电场分布的影响可以忽略不计，在接近山坡断面处的截面时，在山坡两边的坡脚位置附近电场发生畸变，其畸变值超过原位置处电场强度值的1.2倍左右。而在包括山坡在内的截面的电场分布，不仅山坡的坡脚处电场会发生变化，且在山坡的顶端出电场会发生畸变。

4 分析影响山坡电场计算的影响因素

4.1 山坡高度对其电场计算结果的影响

在上述的计算模型中，对导线及其山坡两端的山坡坡脚位置不改变，及图2（a）中 k1＝k2＝5 m，坡脚位置分别为y＝±5 m的情况下，只改变山坡左右侧山坡的角度α，β，从而随着山坡角度改变，山坡的高度h也相对的发生了改变，其高度随坡角的变化情况如表2所示。

表2 α和β取不同值时山坡的高度Tab.2 Height of the slope whileαandβ take different values

其仿真结果中在x＝0 m处截取的电场分布曲线如图7。

图7 H不同取值时电场仿真计算结果Fig.7 Electric field simulate calculation results while H takes different values

由图7及表2可知，当α＝β时，而随着角度的增加，其山坡高度越高，在坡脚处电场的减弱程度也越大，山坡坡顶的电场的畸变越明显，当α＝β＝50°时，坡顶电场强度达到8 kV/m以上，但在山坡的坡脚的两边，其变化情况相同，主要由于其几何位置相对于y＝0对称，所以其变化情况也对称。

4.2 山坡角度对其电场计算结果的影响

当山坡高度h不变时，α≠β的情况下，取α＝30°不变，改变β的角度，随着β的改变，其山坡右侧山坡的坡脚位置也发生了改变，其变化情况如表3所示，取高度h＝5 m时，分别在α＝30°，β取不同角度时在x＝0 m处截取的电场分布曲线如图8所示。

表3 β取不同值时山坡的右侧坡脚位置Tab.3 Position of the hill fort right side while takes different values

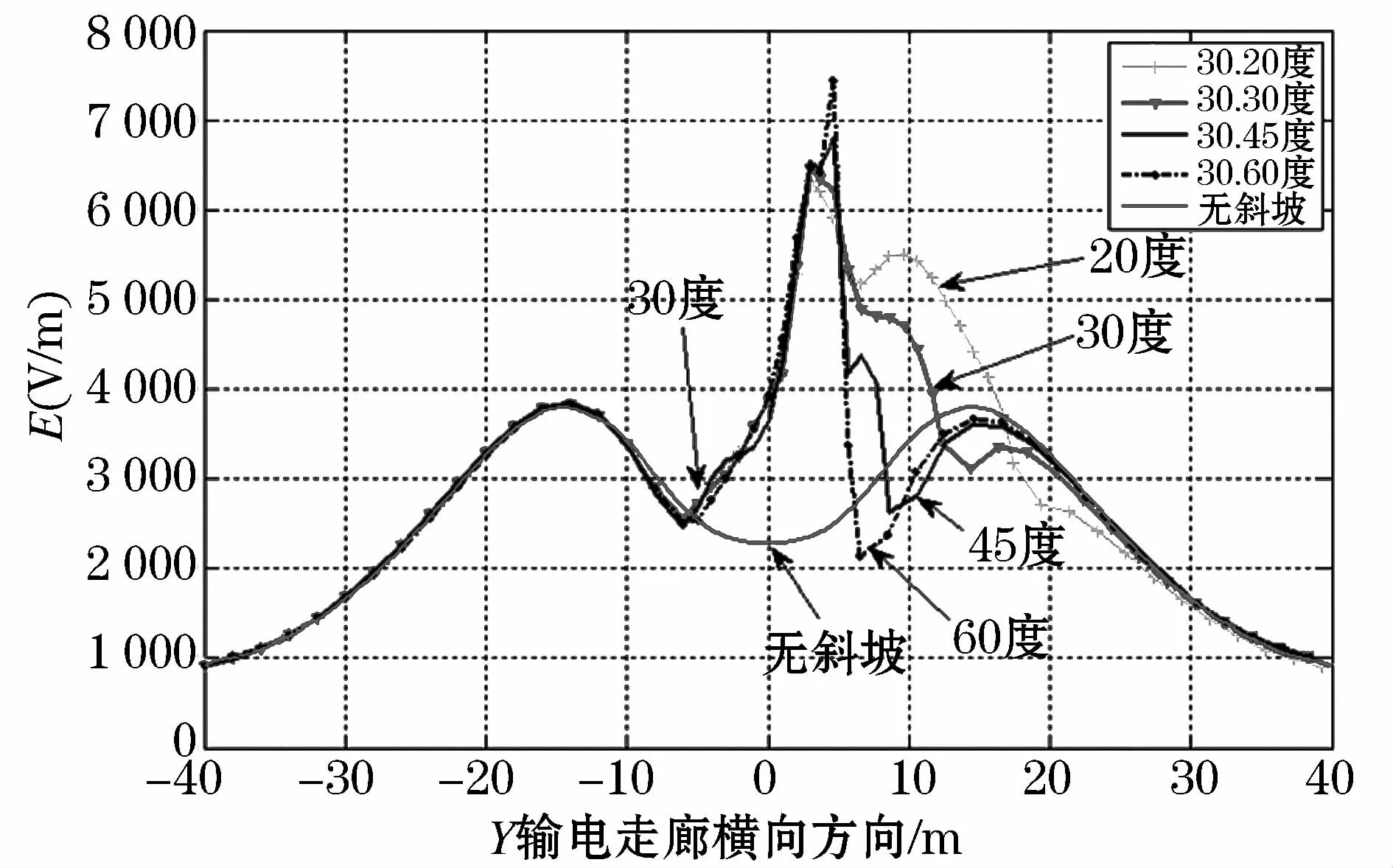
图8 β取不同角度时在x＝0m处的电场对比结果Fig.8 Contrast results of the electric field in the x＝0 m whileβtakes different angles

从图8中可知，高度不变时，β越小，右端起坡位置距离山坡顶点越远，山坡右端的电场的畸变位置也越远，随着角度的增大，在坡脚处电场强度的减小程度越大，在坡顶处的电场畸变越大。

4.3 山坡与导线的相对位置变化时对电场计算结果的影响

由上述的仿真中可得，当取α＝β＝30°时的仿真的，其观察效果比较好，所以在改变山坡与导线的相对位置时，选择α＝β＝30°，山坡高度为h＝5 m当，输电线与山坡山脊平行时，山坡左侧山坡坡脚的位置分别在y等于－15 m，10 m，5 m，0 m处，其在x＝0 m处的电场分布的截线对比结果如图9所示。

由图9可知，随着山坡坡脚在Y轴不同位置，其山坡周围的电场变化趋势相同，均在靠近山坡的起坡坡脚处电场开始逐渐减少，然后沿着山坡逐渐增大，其坡脚位置越接近输电线的边相，坡脚对电场的减小程度越大。

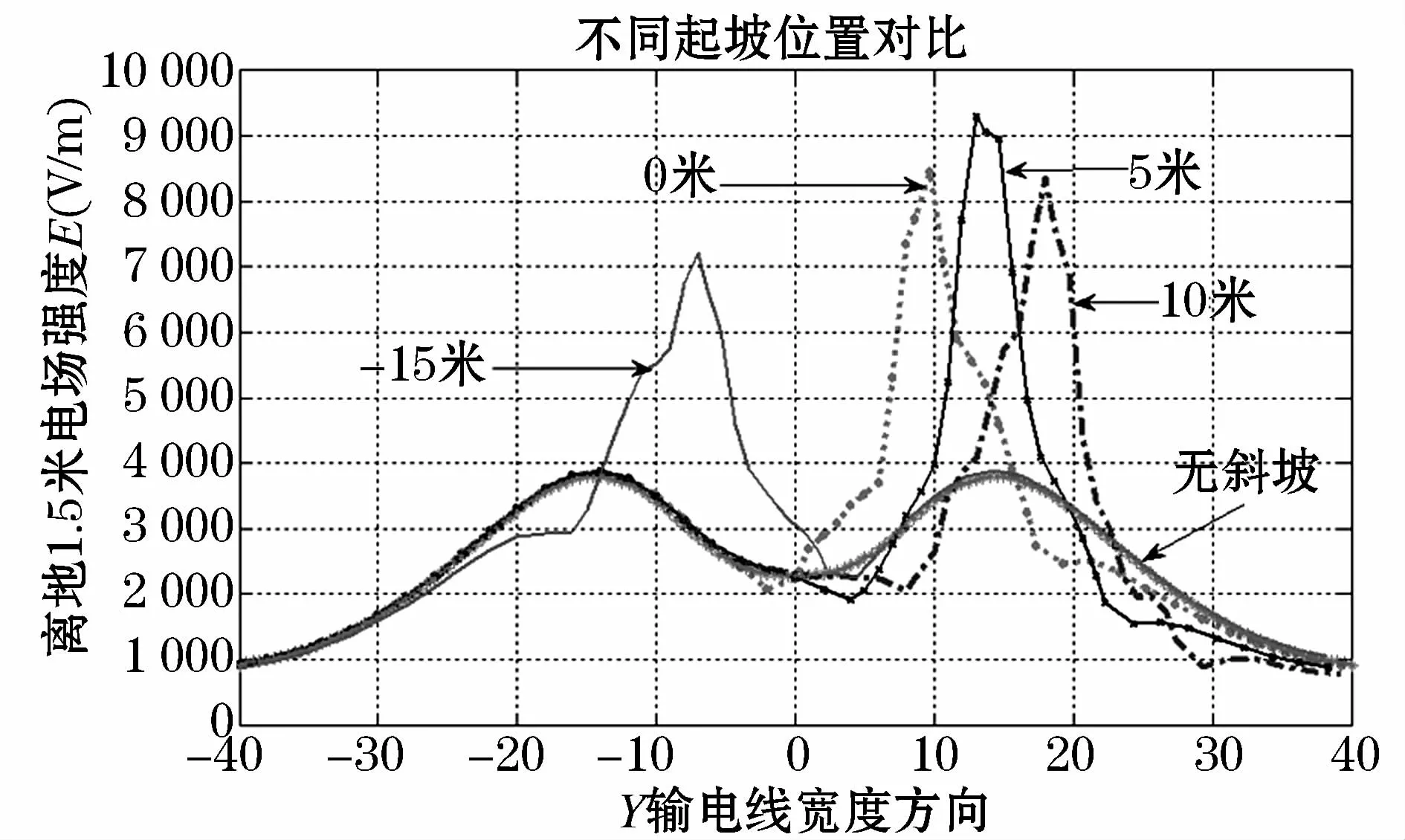
图9 不同坡脚位置时x＝0 m处电场对比结果Fig.9 Comparison results of the electric field in x＝0 m when the hill foot at different positions

当输电线与山坡的山脊之间成任意夹角，其角度为γ时，图2中的俯视图（c）将变为如图10所示；在不同的夹角γ下，其中其夹角分别为γ＝20°，γ＝30°，γ＝45°，γ＝60°，在 x＝0 m处的电场分布对比结果，如图11所示；当γ＝60°时，整个区域电场的三维仿真结果如图12所示。

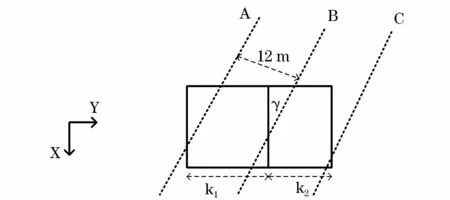
图10 输电线与山脊之间夹角为时的俯视图Fig.10 The top view while the angel of the transmission line between the ridge is equal toγ

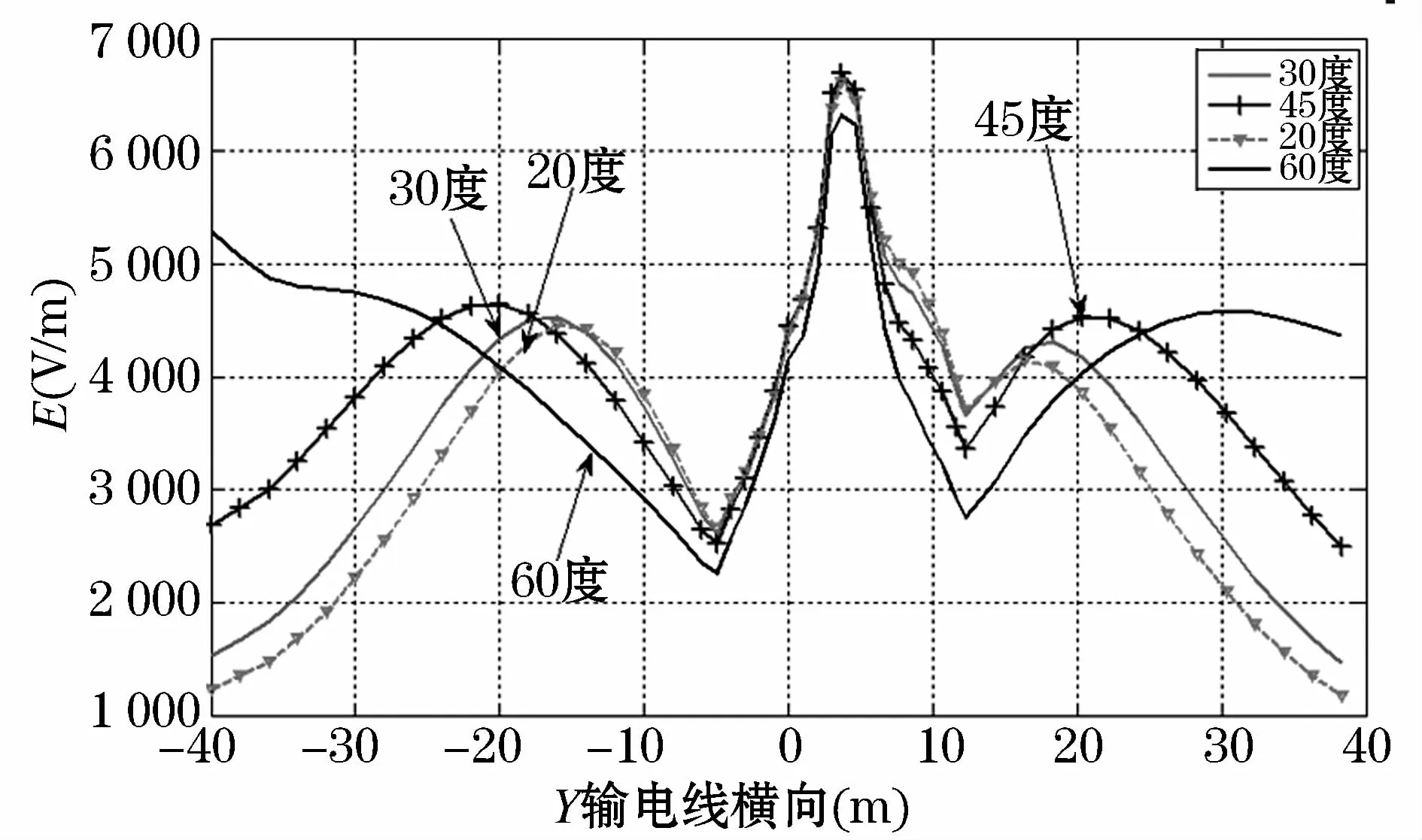
图11 γ不同取值时x＝0 m处电场对比结果Fig.11 Electric field contrast results in x＝0 m whileγtakes different values

图12 γ＝60°时三维电场仿真结果Fig.12 The 3-D electric field simulate resultswhileγ＝60°

由图11可知，随着输电线与山坡走向的夹角增大，在山坡的山坡起坡位置处，其对电场的减弱程度也随之增大，而且其电场的变化趋势，随其角度的增大，逐渐往 Y轴负方向平移，电场的幅值也逐渐减小。

图12是γ＝60°时，计算得到的三维电场仿真结果，从图中可以看出由于γ＝60°时，输电线与山坡的相对位置变化较大，所以在x＝0 m处的电场在边相对应位置其场强峰值位置改变较大。但是其电场的变化趋势没有变化，由此说明其变化只是因为在x＝0 m处的截面内，输电线与地面之间在相同的X，Y坐标位置处，其对于的高度值发生了变化。由此可知输电线与山坡之间的相对位置是影响山坡周围电场的计算的一个重要因素，所以在实际情况中，对山坡周围电磁环境评估过程中，该因素应该加以考虑。

5 结束语

基于模拟电荷法建立的山坡的三维计算模型两个坡面同时存在的情况，对其山坡的电场计算更接近实际情况，且此方法的运用，不受地面是否平坦的影响；更具有普遍性。山坡的坡脚区域对输电线的电场有一定的减弱，其减弱的程度与山坡的起坡角度有关，山坡的起坡角度越大，坡角对电场的减弱程度越大。山坡与输电线的相对位置发生变化时，其中输电线与山坡山脊之间的夹角是影响其电场计算的一个重要因素，在对山坡周围的电磁环境进行评估的过程中应该给予重视。