基于多模型状态估计的光伏阵列MPPT技术*

聂晓华，张晓倩

（南昌大学信工学院，南昌330031）

0 引 言

在实际应用环境中，因外界环境、光伏阵列本身和功率变换器等复杂应用环境影响，使光伏阵列P-U曲线具有时变非线性、状态突变造成的多峰值，难以用准确的数学模型描述［1］。针对在局部遮挡或本身特性不一致情况下光伏阵列多峰功率-电压曲线（以下简称P-U曲线），国内外提出了多峰最大功率点跟踪（Maximum Power Point Tracking，MPPT）算法［2-8］。文献［9］提出一种扰动观察法和递推最小二乘估计相结合的光伏系统控制策略，采用递推最小二乘估计对该电流值进行滤波以削弱量测误差。

针对复杂应用环境下光伏阵列具有多个状态组成的多峰P-U曲线，在建立了离散非线性状态空间模型基础上，把MPPT控制视为非线性时变系统辨识问题，提出克服复杂应用环境影响的基于交互多模型（Interacting Multiple Model algorithm，IMM）估计的MPPT算法，与递推最小二乘估计相比，该方法能够在多峰P-U曲线情况下准确定位最大功率点，适应外界快速环境的变化、抑制测量和状态噪声的影响。

1 光伏阵列多模型MPPT控制策略

鉴于采用电压、电流实时信号的采样数据方法，能够更直接地体现具有多种干扰影响因素的P-U曲线，方便分析复杂应用环境对各种全局MPPT方法的影响机理，建立如下所示P-U曲线状态空间模型：

式中xk为k时刻系统的n维状态矢量，uk为控制输入矢量，yk为测量矢量，wk为状态噪声矢量，vk为测量噪声矢量，wk、vk为零均值高斯白噪声，分别具有协方差阵Qk和Rk，Hk为测量矩阵。

IMM算法假设系统具有多种状态，每一种状态对应一种模型，系统在任意时刻的状态都可以用给定的模型的一种来表示，而运动状态的变化及运动模型的切换用齐次马尔科夫链表示，滤波结果是多个滤波模型结果的加权综合［10］。

在IMM算法中，模型状态噪声方差是设计给定的。为自适应系统状态变化，加宽滤波器的带宽，本文作者提出了改进的IMM算法，该算法通过模型转换概率μi（k－1）和先验的马尔可夫切换概率πij，辩识及调整两个模型的状态噪声方差Qj（k），在不降低系统跟踪精度的前提下，对较大范围突变状态能以较大的状态误差保持快速响应，消除量测噪声的干扰，能显著提高跟踪系统精度。

本文采用两个量测噪声相差较大的线性模型，状态噪声小模型量测噪声为0.01，状态噪声大模型的状态噪声为10。改进IMM算法结构图如图1所示。

图1 改进IMM算法结构图Fig.1 Structure diagram of the improved IMM algorithm

（1）输入交互

模型预测概率：

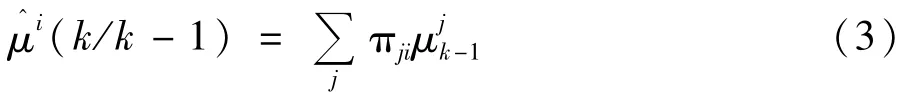
概率混合：

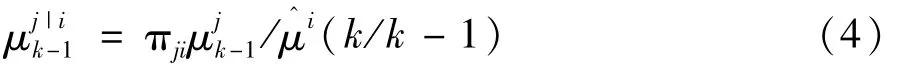
状态估计混合：

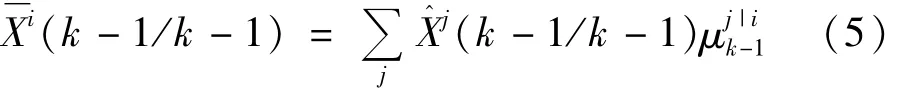
协方差混合：

（2）滤波计算

利用本周期的量测进行辩识并调整各模型状态噪声方差的公式如下：

其中：

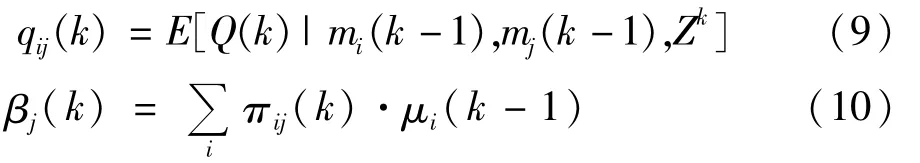
状态噪声方差的调整采用了先验的马尔可夫切换概率πij，这是因为先验的πij考虑到了各种未来可能的突变，具有较好的鲁棒性。

（3）模型概率更新

对于第j个模型，其似然函数为：

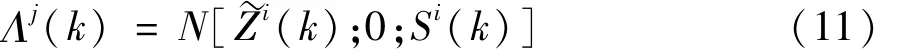
式中N［·］为正态分布密度函数。

模型概率更新：

（4）输出交互

状态估计：

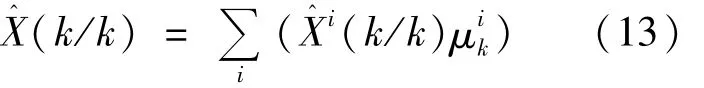
方差估计：

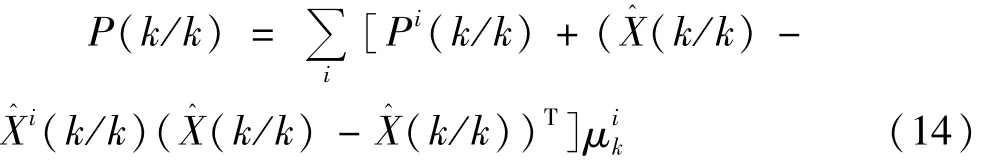
基于改进IMM算法的MPPT控制策略流程图，如图2所示。

通过恒压法定位最大功率点电压范围，改进IMM算法对功率值进行滤波，记录功率滤波值和对应的端电压；识别出多个局部功率峰值。在滤波结束后，对记录的滤波后值进行比较定位出最大功率点及对应的端电压，完成光伏阵列最大功率点跟踪，通过PWM控制光伏阵列工作在最大功率点。

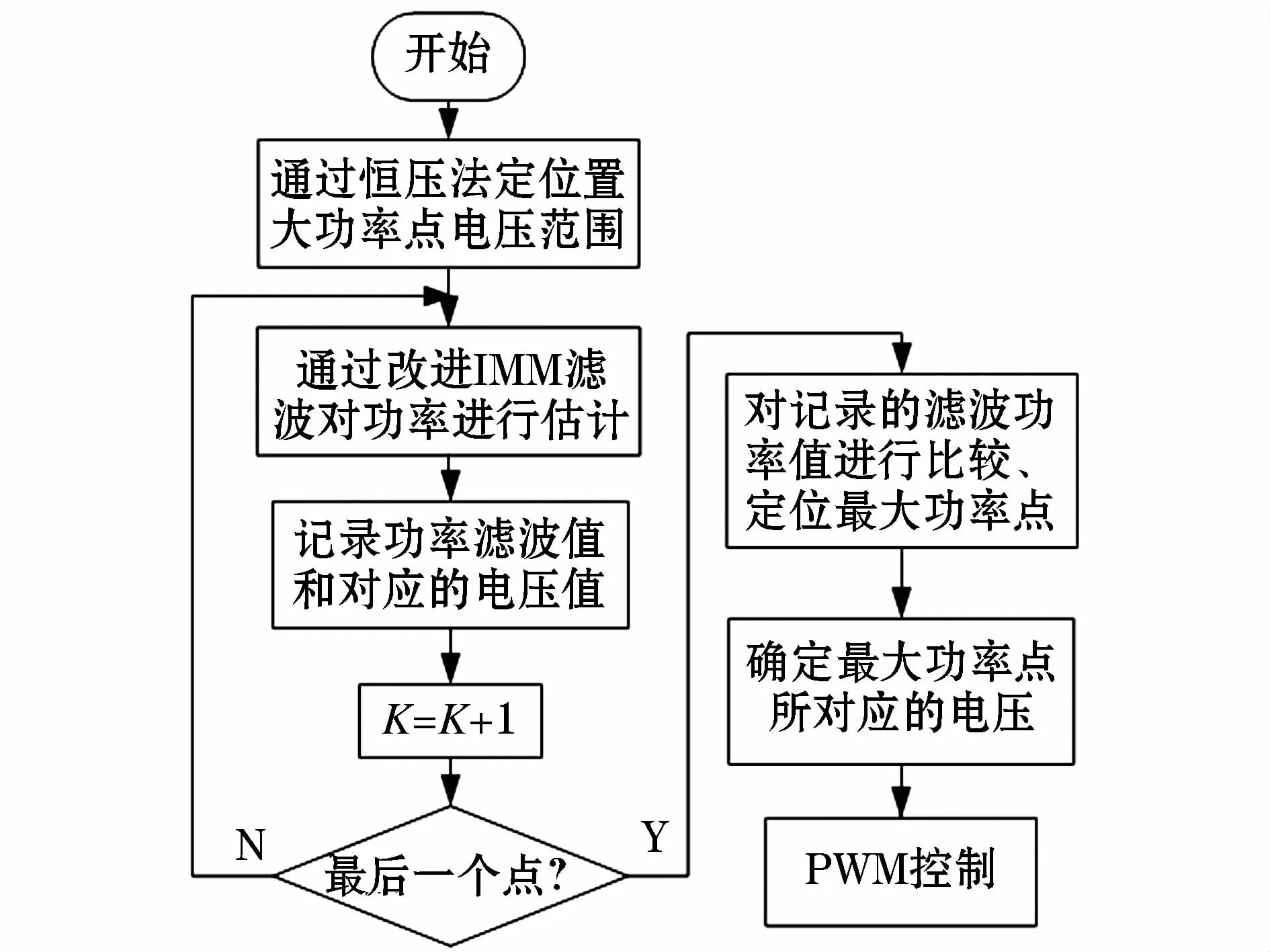
图2 基于改进IMM算法的MPPT控制策略流程图Fig.2 MPPT control strategy flow chart based on improved IMM algorithm

2 仿真与实验

2.1 仿真实验

光伏阵列MPPT升压控制电路原理图，如图3所示；图中，光伏阵列采用12块哈博HBM（175）太阳能电池组成的3×4阵列，每块光伏电池的参数如下：最大功率175Wp，最大功率点电压35.4 V，短路电流5.29 A，开路电压44.2 V。设定电压及电流传感器的量测误差为1%，环境温度、光照分别为25℃、1 000W/m2，在两种阴影情况下，仿真出光伏阵列带噪声的稳态多峰P-U曲线，如图4所示。

针对图4所示两种阴影情况，对改进IMM算法进行仿真验证，改进IMM算法参数选择：采用两个量测噪声相差较大的线性模型，模型1状态噪声取0.01，模型2的状态噪声取10，量测噪声取0.1，初始状态转换概率都取0.5，一步转移概率矩阵取［0.98 0.02；0.02 0.98］。采样步长取0.1 V，进行100次Mont-carlo仿真并统计功率均方根误差值（RMSE），带噪声的最大功率点（虚线）和改进IMM算法跟踪结果进行统计比较（实线），如图5所示。

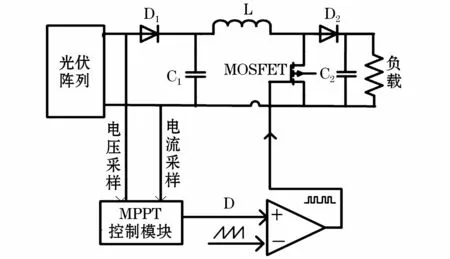
图3 MPPT控制原理图Fig.3 MPPT control principle diagram

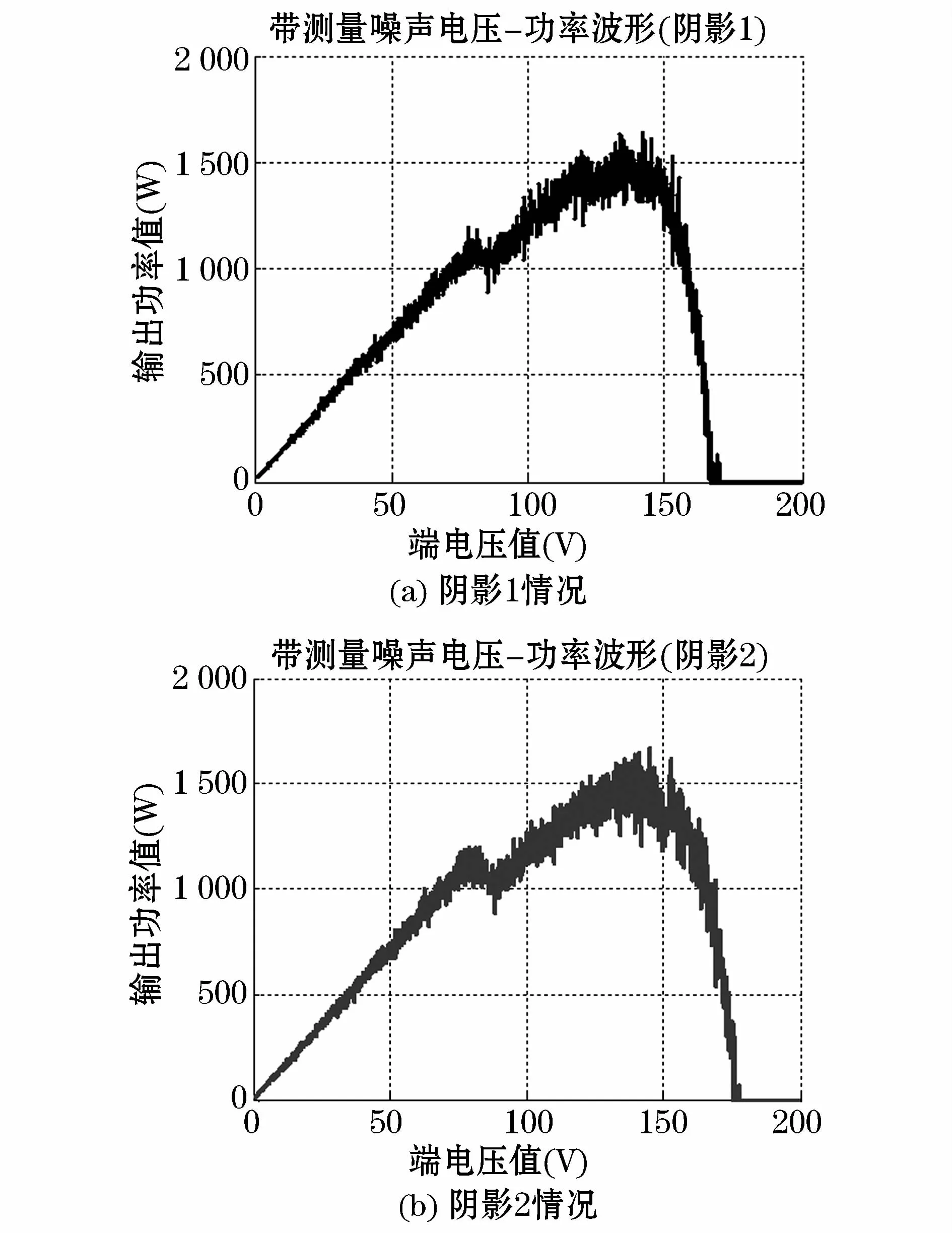
图4 局部阴影下带量测噪声的光伏阵列P-U曲线Fig.4 Photovoltaic array P-U curve with measurement noise under partial shading

从图5看出，改进IMM算法跟踪结果达到准确跟踪多峰P-U曲线的目的，算法能够自适应跟踪P-U曲线的突变，跟踪结果的误差（尤其是最大功率点）显著降低，提高了最大功率点定位准确性。

图5 跟踪统计结果Fig.5 Tracking statistics result

2.2 实验比较

建立如图3所示3×4排列的光伏阵列（光伏电池参数同上）和升压Boost电路实验平台，对本文所提MPPT控制策略与递推最小二乘估计MPPT控制策略进行实验比较。Boost电路实验平台的控制器由K60P100SYS芯片实现，Boost电路参数为：L＝4 mF，C1＝220μF，C2＝470μF，PWM频率 fs＝20 kHz。电压电流传感器测量误差为±1%。实验时测量室外温度、光照分别为28℃、900W/m2，本文所提控制策略与递推最小二乘估计进行比较的实际测量波形，如图6所示。

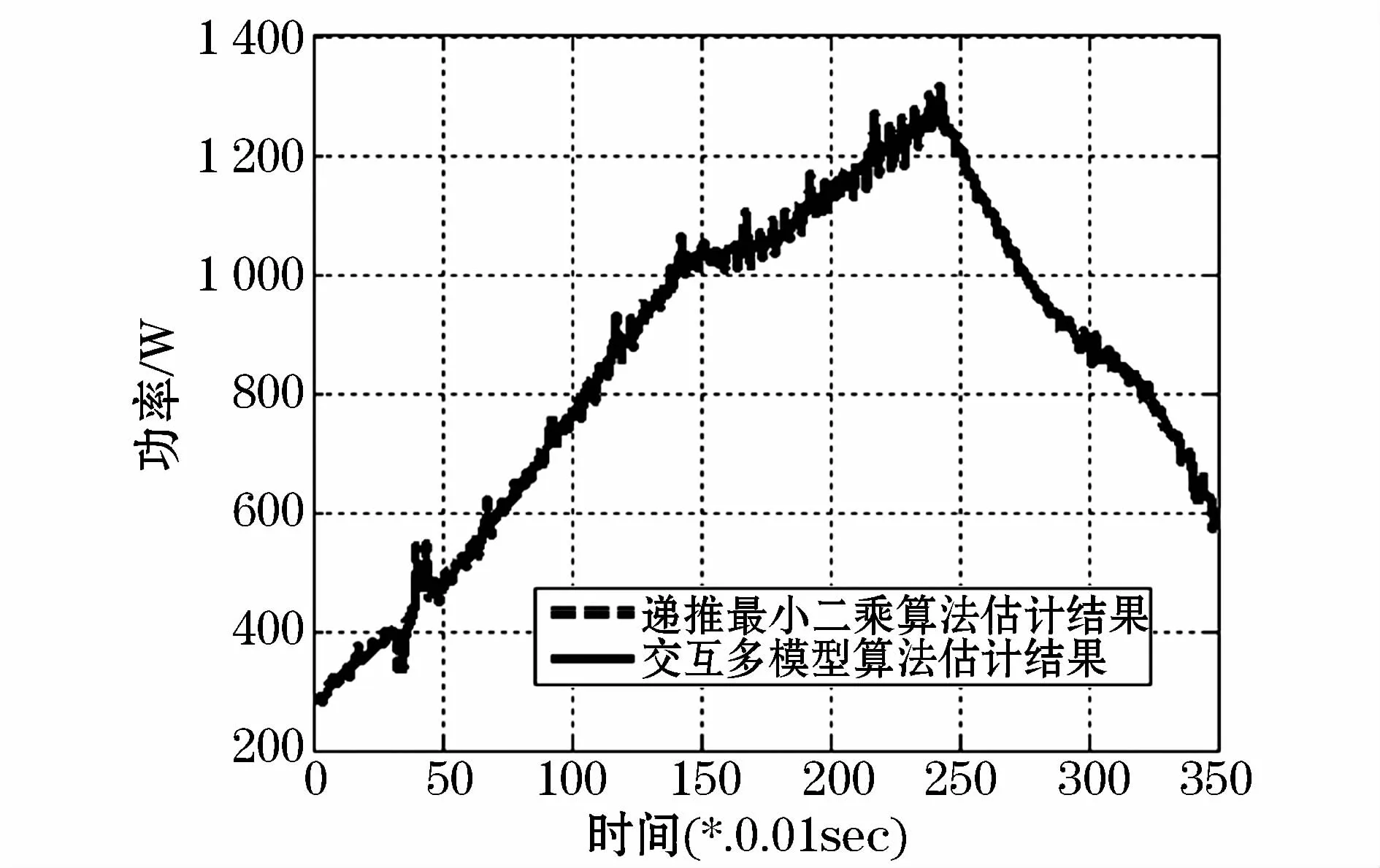
图6 实际测量波形Fig.6 Waveform of actualmeasurement

从图6可以看出，递推最小二乘估计MPPT控制策略误差较大，本文所提改进IMM状态估计MPPT控制策略提高了跟踪精度。

3 结束语

采用现代控制状态空间分析方法，对局部阴影条件下的光伏阵列多峰特性曲线进行动态建模，交互式IMM算法是多个状态模型组合以适应多状态变化的多模型状态估计算法，克服了线性滤波容易发散、误判的缺陷，更适应于跟踪光伏阵列多峰特性曲线，并能准确定位最大功率点。通过仿真与实验比较，改进多模型状态估计MPPT控制策略的稳态跟踪精度优于递推最小二乘估计MPPT控制策略。