基于引入模拟退火思想的改进粒子群算法的电动汽车充电站最优规划*

闫天泽，邱晓燕，刘延博，唐可，万成江

（四川大学智能电网四川省重点实验室，成都610065）

0 引 言

随着化石燃料的日益枯竭，以及全球环境问题的日益恶化，新能源产业成为了替代传统化石燃料解决能源危机的重要举措，受到了各个国家的大力扶持。随着电动汽车技术，特别是电池技术的发展，以及一些国家在政策上的大力支持，电动汽车在过去的十多年间得到了快速发展［1］。

电动汽车充电站可以为电动汽车提供充电、维修等多项服务，是未来电动汽车产业发展所需要的重要基础设施。目前，国内外学者对电动汽车的充放电行为和充电站的选址和定容方面做了大量的研究。文献［2-4］研究了电动汽车大规模接入电网对电网造成的影响。文献［5-7］研究了电动汽车的负荷特性，并分别提出了不同的模型和计算方法。文献［8］提出了基于分时电价的电动汽车有序充电策略，达到了削峰填谷的目的。文献［9］以博弈的思想采用全局最优的定价策略，使充电商和用户达到利益最大化。文献［10］分析电动汽车充电站的接入方式和影响充电站规模的相关因素。文献［11］采用分层递进的方法对充电站的规划求解。然而这些方法都没有将一些影响充电站规划的实际因素（尤其是交通信息）纳入规划模型中。并且电动汽车负荷具有分布不均和流动性大的特点，因此服务区的划分尤为重要。

文章将交通信息和用户的充电成本纳入到规划的数学模型中。对原始粒子群算法做出改进，提高算法准确率与效率。用加权Voronoi图和引入模拟退火思想的改进粒子群算法联合求解，很好地解决了待规划区域服务区划分、充电站的选址和定容问题。

1 数学模型

1.1 选址模型

电动汽车充电站的建设成本不仅要考虑建站的征用土地、基础建设、购买充电设备等费用，还需要考虑充电站每年设备维护成本。以往的文献在对充电站规划问题只考虑充电商的利益。因此，文章在进行电动汽车充电站优化规划时，创新性地不仅考虑了电动汽车充电站建设运行的成本，还将用户的充电成本纳入模型中，形成全社会总成本。

（1）平均每年电动汽车充电站j的投资费用为：

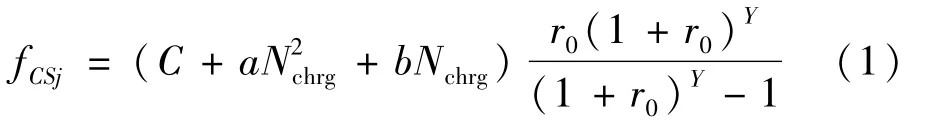
式中fCSj表示电动汽车充电站j折算到每年的投资费用；C表示修建充电站所需征用土地和基础建设的固定投资成本；a是包含购买充电机、配电变压器修建成本和铺设输电线路等有关的等效投资系数；b为充电机的单价；Nchrg为充电站j所需安装充电机数量；r0为贴现率；Y为运行年限。

（2）电动汽车充电站j每年的运行维护费用主要包括设备维修、折旧费用，员工工资等，可以按初期投资的百分比进行计算，表达式如下：

式中frj表示电动汽车充电站j的每年运行投资费用；σ代表比例系数。

（3）用户的充电成本指用户有充电需求时候，从充电需求点驶入充电站的空驶电量消耗费用，以及用户的排队等待费用。其表达式为：

式中fcoustomerj表示平均每年电动汽车充电站j的服务

式中F表示充电站规划方案折算到每年的全社会总成本；N表示需要修建的电动汽车充电站的数量。如今随着经济的发展，土地征用等费用越来越昂贵，充电站的初期投资成本过大。以往的文献没有考虑初期投资对总成本的影响。因此文章引入投资权重系数概念，用φ表示充电站初期投资权重，ψ表示运行成本权重，τ表示用户成本权重。文章设定φ＝0.5，ψ＝0.2，τ＝0.3。

1.2 基于M/M/s排队理论的定容模型

电动汽车的充电需求是随机的。文献［13-14］用排队论中的M/M/s模型模拟电动汽车驶入充电站的充电行为。文献［15］指出在相同服务速率下，采用单队列排队方式的等待时间较采用多队列排队方式的等待时间大幅降低。一般情况下，虽然电动汽车车主非常关心排队等待时间，但在电动汽车数量一定的时候，排队等待时间会随着充电站所安装的充电机数量的增加而减少，因此电动汽车充电站的充电机数量应该基于排队等待时间的期望下进行配置。电动汽车排队等待时间期望的数学模型为：区域内电动汽车用户在充电路途中所消耗的费用。fDT表示用户有充电需求时的空驶损耗成本；fQT表示用户排队等待成本；ζ表示城市出行时间成本；β表示城市道路曲折系数，为城市中两点的实际距离和直线距离的比值，文献［12］归纳了常见交通网络结构中4种典型的曲折系数；Eij表示充电需求点i到所属充电站j的欧几里德距离；nev为每个交通节点平均每天有充电需求的电动汽车数量；E1km为电动汽车单位耗电量；pe为电价；Wqj表示各个充电站的排队等待时间期望。

因此得到全社会总成本优化模型的具体数学表达式如下：

式中Wt为电动汽车排队等待时间；λ表示在单位时间内，服从泊松分布的电动汽车到达充电站的数量；μ表示充电机的充电速率；ρ＝λ/μ表示充电机的平均服务效率。

如果排队等待时间期望Wt不超过最大排队等待时间期望Wmax，通过对式（5）求反函数来求得充电机数量Nchrg很困难。因此文章采用遍历法求充电机数量Nchrg，设定一个最大期望时间Wmax，充电机数量的初值为Nchrg＝fceil（ρ），之后逐步增加充电机数量，直至使期望时间小于最大期望时间，则充电机数量Nchrg即为所求。经试验证明，期望时间会随着充电机数量的增加而快速减小。

1.3 约束条件

（1）系统潮流约束

（2）节点电压约束

式中NCS表示待规划区的所要修建的电动汽车充电站个数；Ptotal表示待规划地区的充电总需求量；Smax，Smin分别代表电动汽车充电站的容量上限和容量下限；fceil函数表示求不小于给定实数的最小整数。

2 加权Voronoi图和改进粒子群算法相结合的联合求解方法

2.1 加权Voronoi图

Voronoi图（又称为V图）又称泰森多边形，凭借着其具备最临近特性，近些年来被广泛应用于测绘、考古等领域，尤其广泛应用于地理设施选址方面［16］。V图在电力系统也应用于变电站的规划当中［17］。设P＝{P1，P2，……，PN}∈R2（2≤n≤∞）是平面上 n个互不相同的点的集合，d（p，Pi）表示平面中任意一点p到Pi的直线距离，则Voronoi图可以定义为：

式中 j＝1，2，…，n，且 j≠i。

设 ηi（i＝1，2，…，n）为一组给定的正实数，分别代表平面上n个点的权重，则加权Voronoi图可以定义为：

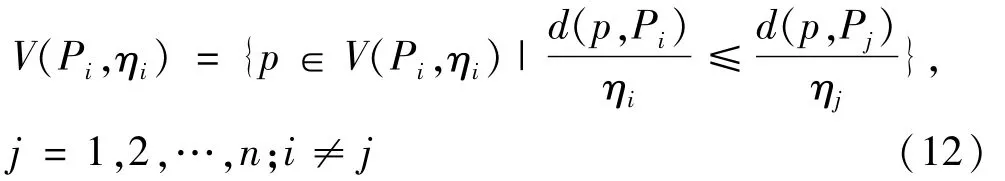
常规的V图不能反映交通流量对充电站规划的影响，因此文章采用加权V图来反映交通流量对充电站规划的影响。按式（13）计算每个服务区域的权重，生成加权V图。然而V图缺乏全局寻优能力，文章用加权V图借助粒子群算法的全局寻优能力进行全局优化。

加权V图权重计算方法：

式中ωi表示各个服务分区的权重；Sck为参考容量；P∑为各个服务分区的充电需求。

2.2 改进粒子群算法

粒子群算法（PSO）在求解优化问题的初期具有很快的收敛速度，然而后期由于所有粒子都向最优粒子靠近，整个种群丧失了多样性，粒子容易陷入局部最优解［18］。因此文章对传统粒子群算法［19］做出如下改进，并根据模拟退火算法（SA）的特性提出了一种引入模拟退火思想的改进粒子群算法（PSOSA）：

（1）改进惯性权重更新机制

粒子群算法的惯性权重是影响算法收敛速度和寻优结果的一个重要因素［20］。当惯性权重取较大的值时，算法具有较好的全局搜索能力；当惯性权重取较小的值时，算法具有较好的局部寻优能力。因此，在整个算法的迭代过程中，首先将惯性权重赋予一个较大的值，使算法在快速地在全局范围内搜寻那个最优解所在的区域，之后随着迭代过程的进行，惯性权重逐渐缩小，使得算法在更小的范围内寻找最优值。因此文章对惯性权重做出如下改进：

式中m是为了保证 ω的取值在［ωmin，ωmax］之间；k的取值影响惯性权重的减小速度；d表示当前的迭代次数；n表示总的迭代次数。

（2）引入模拟退火思想

原始粒子群算法中，对每个粒子的飞行速度控制在一定范围内可以防止粒子产生较大的偏移对整个种群的寻优结果和收敛速度产生影响。但原始粒子群算法没有对每个粒子的位置加以限制。如果一个粒子移动到相比于当前位置较优的位置，并且对全局来说是一个最优位置时，以后的若干次迭代求解都将在该位置的基础上进行，这样会影响算法的性能，使算法很容易陷入局部最优位置。为了使算法跳出可能的局部最优位置，文章将模拟退火思想引入到算法中。

每个粒子运动到新位置后，计算其适应度，若适应度的值优于当前位置，则粒子移动到新位置，如果适应度没有优于当前位置，计算适应度变化值Δe，如果 exp（Δe/t）＞rand（0，1），则粒子移动到新的位置，完成退火操作。其中，t表示当前温度rand（0，1），表示［0，1］之间的一个随机数。温度按照 ti＋1＝tδi衰减，δ表示退火速度。

这样每一个粒子都会经过一个退火的过程，粒子更新位置不仅按照粒子群优化公式移动，还遵循一定概率选择更新位置，从而避免粒子在整个迭代过程中陷于局部最优解，提高整个种群的寻优能力。

3 求解过程

文章的规划过程是：

（1）由电动汽车充电站的最大容量Smax和最小容量Smax，参照式（10）来估计待规划地区所需修建的充电站最大个数Nmax和最小个数Nmin；

（2）设置充电站个数的循环变量N，对于每一个N，按照坐标几何法生成初始站址，并利用加权V图实现待规划地区的各个充电站的服务区域的划分；

（3）根据式（5）和式（6）用遍历法求解每个服务分区内需要安装的充电机数量；

（4）在各个服务分区内利用改进粒子群算法，以全社会成本最小为目标进行优化选址定容，从而得到每一种N对应的充电站最优规划方案；

（5）对所有规划方案排序，选取成本最小的方案作为待规划地区的最优规划方案。具体规划流程见图1。

4 算例分析

4.1 算例模型

文章以南方某市经济开发区的电动汽车充电站规划为例。该经济开发区共有交通节点25个，规划区面积为36 km2，该规划区域的交通结构如图2所示。各个交通节点的交通流量如表1所示。

到规划年预计电动汽车所占比例为15%，充电率为10%。

文章假定每座充电站的固定投资成本C取值100万元；与充电机数量有关的等效投资系数a取2万元/台2；充电机的单价b取10万元/每台；贴现率r0取0.08；运行年限为20年。城市道路曲折系数β取1.3；电价为0.7元/kW·h；电动汽车平均每公里耗电量E1km取0.15 kW·h/km；该地区用户出行成本为20元/h；单台充电机的功率为96 kW；充电站最大容量配置为25台充电机，最小容量配置为6台充电机；充电机的充电效率为90%，同时率为85%。

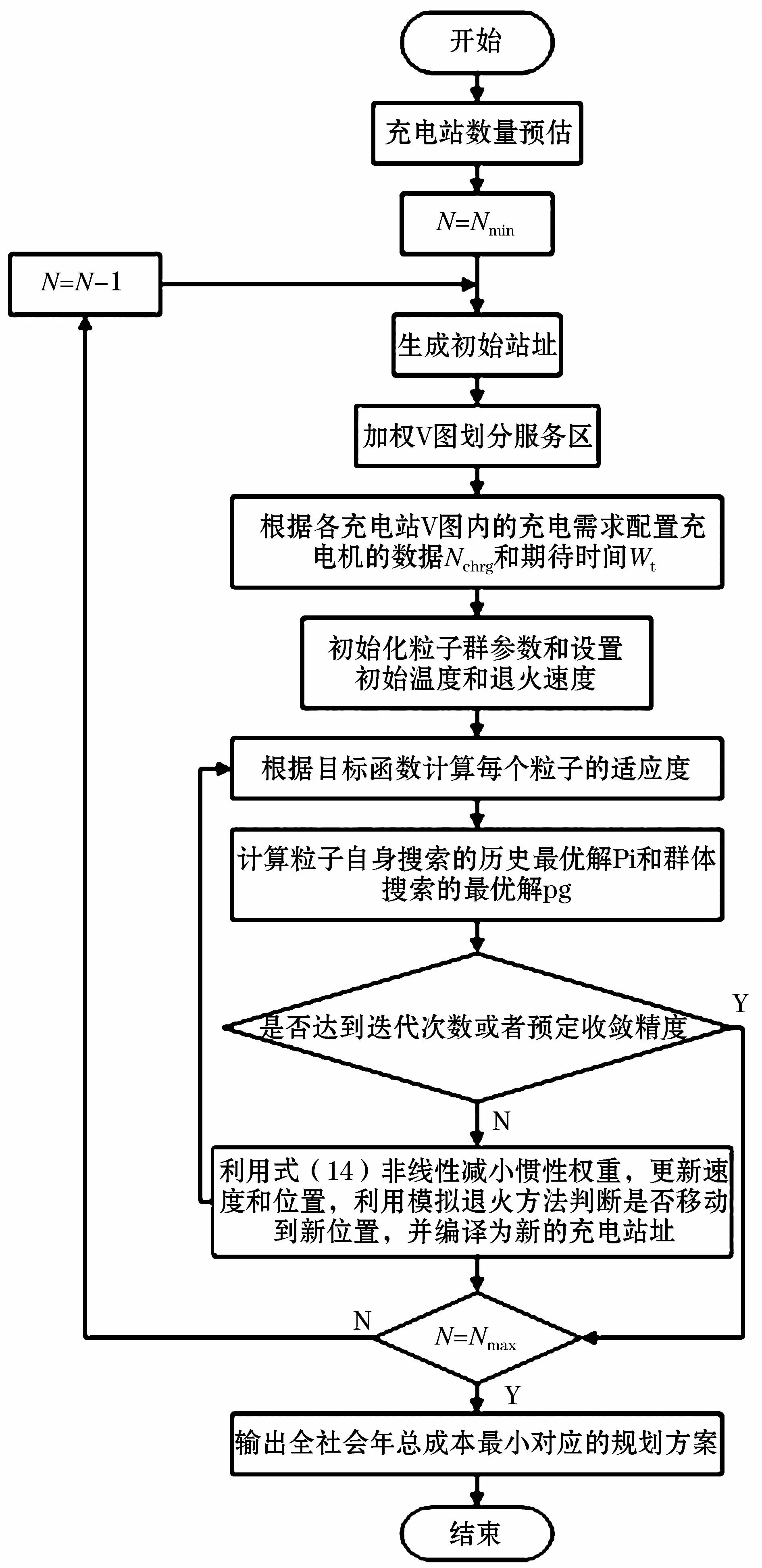
图1 规划流程Flg.1 Planning process

图2 规划区交通结构示意图Fig.2 Schematic diagram of traffic structure in planning area

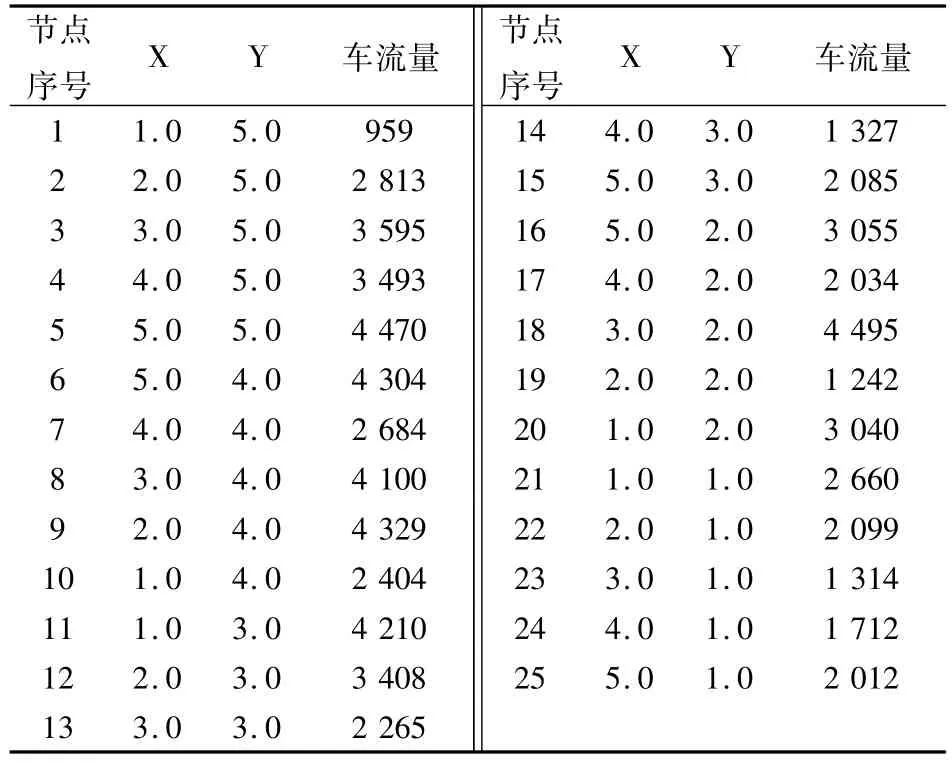
表1 各节点坐标和交通流量Tab.1 Coordinates and traffic flow of each node

4.2 计算结果与分析

根据式（10）预估该地区充电站个数范围为Nmin＝2，Nmax＝7；按照图1所示的流程，以及所提出的规划方法，配置粒子群算法计算得到各种方案的全社会总成本和充电站具体规划结果，全社会总成本计算结果如图3所示。

图3 充电站全社会年成本曲线Fig.3 Social annual total cost curve of charging stations

由图3可以看出，当该地区修建4座充电站时全社会的成本最小，为585.29万元。针对充电站数量为4座时的最优规划方案，得到具体的充电站配置如表2所示，最优规划的服务区划分如图4所示。

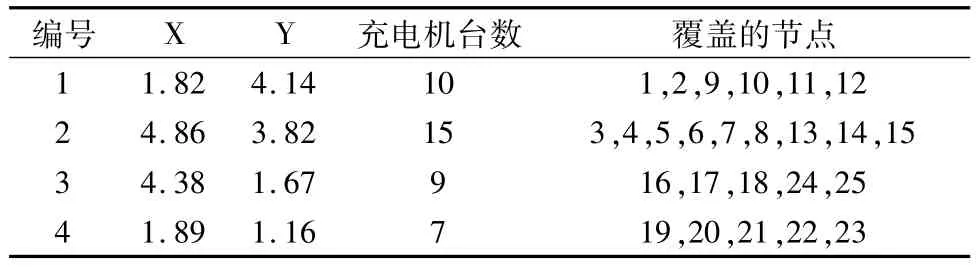
表2 充电站最优配置Tab.2 Optimal configuration of charging stations

图4 充电站服务区划分及选址结果Fig.4 Result of charging stations services division and location

5 结束语

文章研究了考虑交通流量和用户充电成本的电动汽车充电站规划问题，以最小化的全社会总成本为目标，建立了充电站的选址和定容模型，通过对算例用加权V图和引入模拟退火思想的改进粒子群算法联合求解，得出的主要结论如下：

（1）计及交通流量和用户充电成本的模型适用于电动汽车充电站规划问题，得出的结论符合实际情况。对未来电动汽车充电站规划具有一定的指导意义；

（2）改进惯性权重更新机制和引入模拟退火思想的改进粒子群算法在求解效率上更高，可以有效避免陷入局部最优问题。

在文章研究的基础上，未来还应考虑土地价格，地区种类，用户充电习惯，电动汽车类型等实际因素，以使模型更贴近实际情况。