基于细菌觅食算法的故障指示器优化配置研究*
孔涛,贾明娜,怀浩,邱炜,陈羽
(1.山东理工大学电气与电子工程学院,山东淄博255049;2.山东科汇电力自动化股份有限公司,山东淄博255031;3.山东理工大学计算机科学与技术学院,山东淄博255049)
0 引 言
智能电网已成为目前我国电力行业研究的重中之重,是人们为未来电力系统设定的理想解决方案[1]。故障指示器(Fault Indictor,FI)以其能快速故障定位,大大缩短巡线时间,判据简单以及自带通讯模块等优点被广泛应用于智能电网故障自动定位系统中,在缩短停电时间、提高供电可靠性等方面发挥了无可替代的作用。
国内对于故障指示器的配置主要遵循广覆盖、多层次的思路,基本在每个变电站出口处、分支线入口处、电缆与架空线连接处都要装设故障指示器,甚至在平原或空旷地带每一段线路上都要装设多个故障指示器[2]。虽然大范围安装故障指示器能极大的缩短故障停电时间,减少因停电造成的经济损失,但在网络结构复杂的配电网中其设备投资成本及运行维护费用也不容小觑。因此合理规划显得尤为重要。而本文的核心即是在故障指示器的安装位置和数量之间找到平衡点以达到综合经济效益最优。
国内外对于故障指示器的最优配置问题研究较少。文献[3]从经济性角度分析了故障指示器的配置问题并应用免疫算法对其求解,对本文做出了很大启发。文献[4]应用遗传算法对故障指示器进行规划,但仍无法避免遗传算法早熟收敛的问题。面对多变量、非连续规划问题,国内外学者给出了许多现代启发式算法,如免疫算法[5-6]、粒子群算法[7-8]、模拟退火算法[9-10]、遗传算法[11]等,虽然取得了一定成果,但也都存在一定缺陷。因此提出了一种适用于0~1规划的改进的细菌觅食算法(Bacterial Foraging Algorithm,BFA),通过定义进化域的方式确定细菌的前进方向,解决了传统细菌觅食算法只能应用于连续域的缺陷。并且设立电子公告板,避免算法中的迁徙算子有一定几率删除最优解的可能性。
1 故障指示器优化配置的数学模型
通常,大范围的安装故障指示器能极大的提高电力系统的供电可靠性,但相应的其设备投资成本也大大增加。这种可靠性成本与可靠性效益之间的关系即相互矛盾又对立统一。因此,故障指示器的优化配置目标就是要在保证系统供电可靠率的基础上综合考虑设备投资成本、运行维护费用以及系统停电损失等因素以达到综合年费用最少。
1.1 投资费用
由于设备的使用年限不同,故按照等年值法给出故障指示器的等年值投资:

式中N为故障指示器的安装数量;C′FI为故障指示器的一次性投资单价,包括设备采购成本和施工安装费用;i0为现贴率;n0为设备的经济使用年限。
1.2 运行维护费用
故障指示器的运行维护费用CM按其投资的百分比给出,同时现大部分故障指示器均自带组网通讯设备,因此考虑GPRS通讯费用,具体给出:
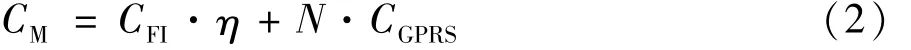
式中η为运行维护费用占投资的比例系数;CGPRS为GPRS通讯年费。
1.3 系统停电损失
故障指示器研究的初衷即当电力系统因故障停电时依靠翻牌或告警的方式快速定位故障区段,减少长线路的巡线时间。而停电时间的减少则会降低系统停电损失。
系统停电损失由公式(3)给出,既包括本区段负荷中断造成的损失,也包括因本区段停电所造成的其他区段停电的损失。:

式中loadi为线路i平均负荷值;λi为线路i的故障率(次/km/年);li为线路 i的长度;C′Li(t)为单位停电损失,为时间的函数;Q为因线路i停电所造成的其他停电区段。
单位停电损失C′Li(t)与用户类型及停电持续时间有关[9],如表 1所示。
由表1可见,不同用户类型单位停电损失不同,但都随着停电持续时间的延长而增大,与停电时间成正比例关系。系统停电时间为:
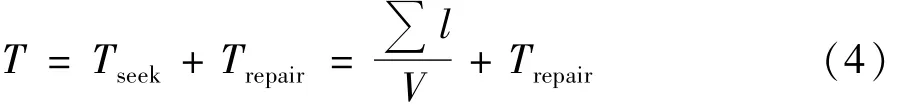
式中Tseek为故障巡线时间;Trepair为故障修复时间,设为定值;V为巡线速度;当本段线路安装故障指示器时,∑l即为本线路长度,故障巡线时间Tseek即为本线路长度与巡线速度的比值;当本段线路未安装故障指示器时,∑l变为本区段算至上级最近安装故障指示器的所有区段线路长度的总和。由此可见,故障指示器的安装与否直接影响了系统停电时间,进而影响了用户的单位停电损失。

表1 用户单位停电损失费用Tab.1 The unit interruption cost of the user
1.4 约束条件
电力系统的正常运行必然要满足供电可靠性要求,此处给出用户平均供电可靠率指标[12]ASAImin,则配置故障指示器下的可靠性指标ASAI必须满足:

1.5 目标函数
故障指示器的安装既会降低停电损失费用,但也会相应的增加投资成本。我们既希望减小经济投资,又希望将停电损失降到最小,因此给出目标函数及约束条件:

式中min f为目标函数,即综合年费用。
2 细菌觅食算法的应用
2.1 细菌觅食算法
细菌觅食算法[13-15]是 K.M.Passino于2002年基于Ecoli大肠杆菌在人体肠道内搜寻食物行为过程中表现出来的群体竞争协作机制,提出的一种新型仿生类群体智能算法。BFO算法主要通过趋化算子、繁殖算子和迁徙算子对目标函数在可行域内进行求解,具有并行搜索、易跳出局部最优解等优点。
(1)趋化算子。大肠杆菌在肠道内觅食的过程中存在两种动作行为,分别是前进和翻转。当在某一个方向上移动一步且检测到此处的食物更充足,也即表述为适应度增大,则继续沿此方向前进,直至达到最大前进次数或适应度不再改变;若细菌检测到适应度没有得到改善则随机另选一个方向前进一个步长,直至完成趋化算子次数。若假设 si(j,k,l)为细菌 i的第j次趋化,第k次繁殖,第l次迁徙后的位置。则下一次趋化操作后细菌的位置为:
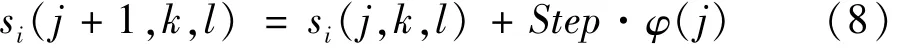
式中Step为细菌移动的步长值;φ(j)表示随机游动的方向;
(2)繁殖算子。繁殖操作遵循生物界“优胜劣汰,适者生存”的法则。在规模为S的种群中,当细菌执行完趋化算子后,将适应度较差的S/2个细菌淘汰,适应度较高的S/2个个体自我复制。算子执行后子代将完全继承父代的优良特性,保护了优良个体,且大大加快了趋向全局最优解的速度。繁殖算子完成后继续执行趋化算子,直至达到最大繁殖次数后执行迁徙算子;
(3)迁徙算子。在细菌觅食的过程中,不排除突发状况的发生导致细菌的死亡或迁徙到另外一个全新的区域。个体以一定的概率Pe死亡,并在解空间内随机生成新个体的过程叫做迁徙算子。与遗传算法中的变异操作相比,迁徙算子并不仅仅是改变DNA上的某一位基因,而是完全生成一个新的个体,即生成一个新的DNA链。这有利于算法跳出局部最优解,增加了种群的多样性,提高了全局搜索能力。
2.2 编码策略
在规模为 S的种群中,每个个体用 s=(θ1,θ2,…θi…θn)表示,其中,个体的维度n与配电网中可以安装故障指示器位置的数目相同。每一维θi可用0或1表示。0表示此处未安装故障指示器,1表示此处装设故障指示器。
2.3 适应度的定义
适应度表征了细菌的优劣程度。适应度函数为:

式中Cmax为一个足够大的正数以保证适应度为正;min f则为目标函数。适应度越大则解越优,算法目的即找到最大适应度的细菌个体。
2.4 细菌觅食算法在配网故障指示器优化配置中的改进
(1)步长的定义。步长Step表示细菌移动一次所远离的距离。设细菌 si=(θi1,θi2,…,θin)移动一个步长后变为 sj=(θj1,θj2,…,θjn),则两次位置之间的距离为:
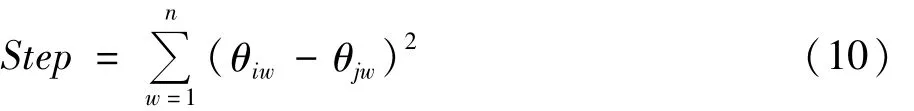
由式(10)可知在二进制编码的规划问题中,若步长Step=x,则只需随机选取x维向量并翻转其值则细菌前进一个步长。如图1所示,若Step=2,则随机选择两个维度如θ2、θ7并翻转其值,则表示细菌前进一个步长。步长值越大则算法速度越快,但相应的精度越低;步长越小则更易找到最优解,但运算时间也会大大增加;

图1 趋化操作示意图Fig.1 Schematic diagram of chemotaxis operation
(2)趋化算子的改进。趋化算子决定了细菌的前进方向,对算法的收敛性和解的优劣程度有着极其重要的影响,是细菌进化的重要操作。
基本细菌觅食算法中,细菌前进一步后若适应度没有得到改善则随机翻转一个角度 φ(j)继续前进,即:

式中 θrand(j,k,l)为当前个体 θi(j,k,l)邻域内的一个随机位置。显然在连续域内自变量的定义域为任意实数,细菌可向任意方向翻转,但是在0~1规划问题中,自变量只能取0或1,定义域为实数范围内离散的点,此时用公式(11)来定义翻转方向显然不妥,因此作出如下改进。
假设当前细菌个体编码如图1中si所示,Step=2。细菌第一步随机的朝某个方向前进一个步长,如随机选取θ2、θ7并翻转其值,则细菌移动到位置sj。分别计算细菌在这两个位置的适应度值f,若f(j)>f(i),则表明移动后的细菌更靠近食物源,因此用新个体代替旧个体。由于θ2、θ7的改变使得个体的适应度更好,因此定义θ2、θ7为进化域不再改变其值,细菌的下一次移动则在进化域的方向上从非进化域中随机选取Step维向量翻转其值比较适应度;若细菌前进一步后适应度并未提高,则重新选取随机方向进行趋化,直至达到最大前进次数;
(3)电子公告板。迁徙算子生成的新个体一般与毁灭的个体拥有不同的位置,即不同的觅食能力,因此有可能产生的新个体更靠近食物源,这样更有利于趋化算子跳出局部最优解和寻找全局最优解。但迁徙算子也有可能以概率Pe毁灭最优个体产生更加远离食物源的新个体,破坏了解的优良性。为避免这种情况的发生设立电子公告板,每次执行完趋化算子后将最优个体位置及其适应度值记入电子公告板,即使迁徙算子以概率Pe删除了当前最优个体,但其位置信息及适应度值已被记录在电子公告板中。在下一轮循环中,只有当趋化操作后的种群中最优个体的适应度值大于公告板中的适应度值时才将其列入电子公告板,否则继续执行趋化算子,直至达到最大趋化次数。
2.5 算法流程
改进的细菌觅食算法在求解配网故障指示器的优化配置流程如下:
(1)初始化参数,趋化算子次数Nc,趋化算子最大移动步数Na,繁殖算子次数Nre,迁徙算子次数Ned以及迁徙概率Pe;
(2)随机生成初始种群,种群规模为S。并计算每个个体的适应度值f;
(3)对每个个体进行趋化操作,并计算适应度值,若新的位置适应度大于移动前的适应度则用新个体位置代替旧个体;
(4)每个个体进行完趋化操作后,选择最优适应度值的个体位置记入电子公告板;
(5)判断是否达到最大趋化次数Nc,若否则重新返回步骤(3),若是则执行下一步;
(6)算法执行繁殖算子,将适应度较低的S/2删除,适应度较高的S/2自我复制。并判断是否达到最大繁殖算子次数Nre。若否则返回步骤(3),若是则执行下一步;
(7)算法执行趋化算子,以概率Pe删除个体。直至达到最大迁徙算子次数Ned后算法结束。
3 算例分析
应用改进的细菌觅食算法对IEEE 33系统进行故障指示器的优化配置的仿真验证。系统接线图及线路编号如图2所示。

图2 IEEE 33节点系统结构图Fig.2 System structure diagram of the IEEE 33 node system
该系统有33个节点,32条线路,每条线路的长度、负荷及故障率如表2所示。
实验所用的故障指示器投资成本约300元/组;经济使用年限约8年;现贴率取0.1;每年的运行维护费用按其投资的10%计算;GPRS通讯年费按60元/年计算。其次,故障修复时间Trepair设为定值为4 h/次;巡线速度为10 km/h。算法参数选择分别为:细菌种群规模S=20;步长Step=2;最大移动步数Na=4;趋化算子次数 Nc=10;繁殖算子次数 Nre=5;迁徙概率 Pe=0.08;迁徙算子次数 Ned=2。采用Matlab7.0进行编程实现算法。算例适应度变化如图3所示。
从算法性能方面分析,在33节点的网络中该算法在迭代25次后便大致收敛并且算法前期有较快的收敛速度。而文献[3]所述的应用免疫算法对12节点系统规划故障指示器时,大致需要迭代200次算法才收敛。虽然数学模型的不同及线路参数的不同会对算法的收敛速度造成一定影响,但性能上的差异显而易见。

表2 IEEE 33系统线路参数Tab.2 Line parameter of the IEEE 33 system

图3 适应度值Fig.3 The fitness value
从解的优劣分析,应用改进的细菌觅食算法求出的综合年费用min f如图4所示。
由图4可见,在使用改进的细菌觅食算法进行故障指示器规划后,综合年费用明显减少。规划后的具体结果见表3。虽然当全线配置故障指示器时其年停电损失要少于优化配置时的损失,但经改进BFO算法规划后其设备投资成本也减少了1.17万元,综合分析,其综合年费用共节约了0.78万元,并且其平均供电可靠率指标虽然有所降低但仍在允许范围内。因此,从故障指示器的安装位置可知,在一些线路较短或负荷较小的区段无需安装故障指示器。
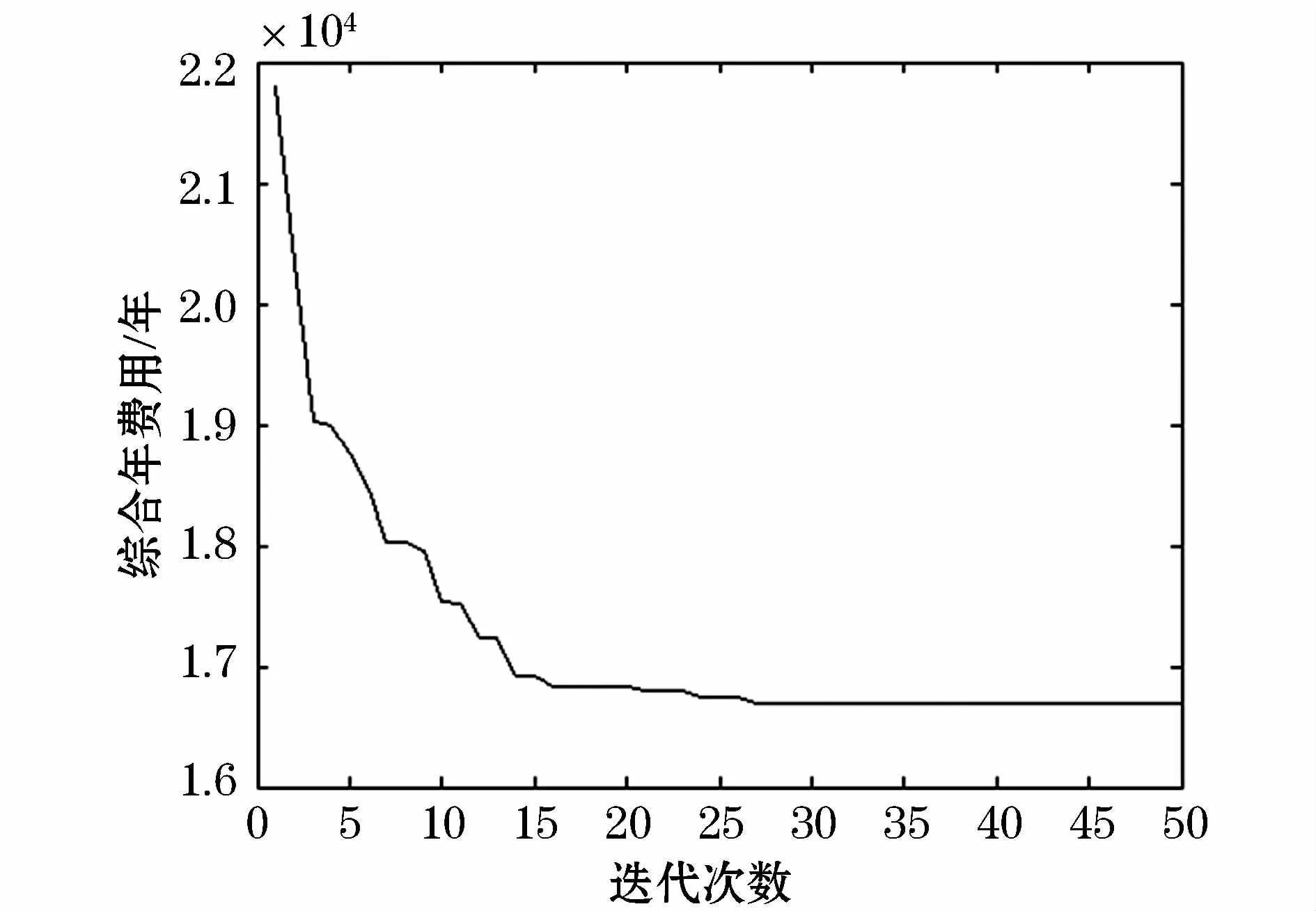
图4 综合年费用Fig.4 Overall annual cost

表3 规划结果Tab.3 The planned result
4 结束语
故障指示器在配网故障自动定位系统中有着举足轻重的地位,但其优化配置问题一直未引起业界学者的重视。本文以设备投资最少、用户停电损失最小为方向,给出了故障指示器的安装与综合年费用之间的关系。应用改进的细菌觅食算法进行求解,通过定义进化域的方法改进了其趋化算子,使之能很好的解决0~1规划问题;并设立电子公告板,避免了迁徙算子有一定几率删除最优解的可能性。算例表明,该算法能很好的解决配网故障指示器的优化配置问题,减少经济损失。

