基于模糊聚类算法的油纸绝缘缺陷识别

王艳，徐祥海，侯伟宏，朱军，高标，章洁菁

（国网浙江省电力公司杭州供电公司，杭州310016）

0 引 言

油浸纸绝缘结构是电力变压器内绝缘系统的重要组成。该结构在变压器中起支撑、绝缘和固定作用。在长期运行过程中受到电、热、机械等多因素影响，导致绝缘性能下降。局部放电是油纸绝缘损伤的重要因素［1］。纤维纸因未充分浸渍形成气穴、金属导体突出部位电场强度增强或绕组连接处长时间过热均会导致并加速局部放电发生。与IEC 60270［2］、GB／T 7345-2003［3］局部放电脉冲电流法相比，局部放电超高频检测具有检测频率高、信息量大、能够有效避开低频电磁干扰和适用于在线检测等优点，它通过传感电力设备内部局部放电所产生的超高频电磁信号，实现抗干扰和局部放电的检测与定位［4-7］。文献［8］采用逐层最优小波去噪算法提取局部放电信号特征量，结果显示去噪信号具有波形畸变率低和幅值误差小的特点。通过小波包多尺度分析和网格维数提取变压器典型放电模型产生局部放电超高频信号特征量，并采用神经网络对其进行识别［9-10］。

局部放电信号特征量能较好反映变压器内部绝缘状况。本文模拟变压器内部绝缘缺陷，构造4种局部放电模型。采用对比不同小波层数和小波尺度寻求最优小波去噪效果。提取小波去噪前后局部放电超高频信号特征量即小波能量和网格维数，组成综合识别矩阵进行聚类及缺陷识别。采用模糊C-均值聚类算法对综合向量进行聚类分析及识别。验证了超高频信号小波包多尺度能量参数和网格维数能有效表征四种局部放电模型特性以及模糊算法对油纸绝缘缺陷识别的适用性。为评估绝缘状态、预测绝缘寿命打下坚实基础。

1 油纸绝缘局部放电试验

本文试验回路根据标准GB 7354-2003，搭建在双层屏蔽室内，局部放电超高频测量系统及试验接线示意图，如图1。其中：升压变压器由无晕试验变压器和自耦调压器构成；保护电阻R起限流保护作用，阻值为7 kΩ，耐压为50 kV；高压耦合电容是1 000 pF，耐受电压为60 kV；测量系统包括数字示波器（LeCory7200）、超高频四阶希尔伯特分形天线H［11］、电流传感器 C、信号放大器、50Ω同轴电缆。脉冲电流传感器通常在50 kHz至10 MHz频带内具有良好的测量线性度和幅频特性。脉冲电流传感器测量信号和希尔伯特分形天线分别经长5 m的同轴电缆连接示波器。试验同时接收两种传感器C和H的信号。由于示波器的高通截止频带为1 GHz，因此试验采样率选为1 GHz。示波器的采样率设置为1 GS／s，模拟带宽为 1 GHz。

变压器内部主要局部放电类型：油间隙放电；沿面放电；悬浮电位放电；油中气泡放电；固体绝缘中的空气间隙放电。本文针对变压器绝缘内部放电形式和特点，利用变压器专用纤维绝缘纸板和ABB矿物油构建局部放电试验模型。构建4种油纸绝缘典型放电模型模拟典型绝缘缺陷：油中气隙放电、电晕放电、楔形油隙放电和沿面放电。据标准CIGRE II采用黄铜电极和油纸绝缘模型搭建试验模型系统，电极及各放电模型尺寸见图2。气隙放电模型在绝缘纸板预处理后制作。气隙放电模型由上下两层Φ 75 mm实心纸板和中间一层外径Φ75 mm、内径Φ 60 mm的环形纸板共同构成，为防止矿物油渗入气隙模型，用环氧树脂胶对其结合处进行密封后并用夹板加紧至模型投入使用。为防止电极接引线和高压引线处发生电晕放电，高压引线采用直径为Φ10 mm的铝管，电极螺帽为专门设计加工的球形螺帽；电极表面和边缘均经过特殊处理尽可能消除电极表面尖角或毛刺的影响；局部放电试验前先将一次筛选后的试样在真空箱中经过90℃、2 h干燥处理，并对试样进行室温48 h真空充分浸油、祛气以降低微水含量和气泡对绝缘耐压强度的影响；浸油后试样的微水含量均值为0.8%，确保真实放电类型与放电模型一致。预处理后试样进行二次筛选确保局部放电试验四组共40个试样形状尺寸相同、纸板无损伤无异物。

图1 局部放电试验系统Fig.1 PD experiment system

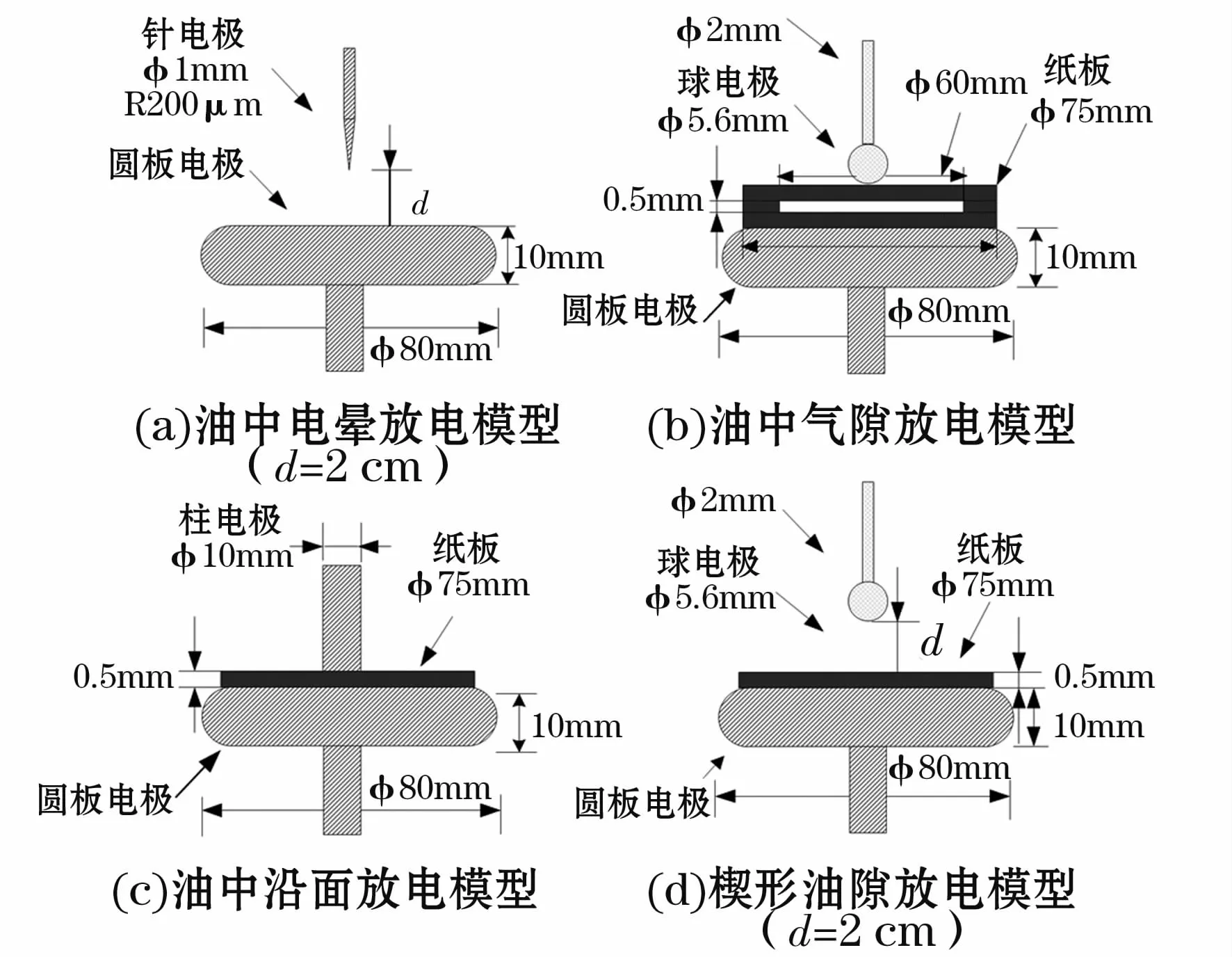
图2 4种局部放电模型Fig.2 4 kinds of PD models

图3 标定电路Fig.3 Calibration circuit

试验采用逐步升压法加速局部放电过程。试验电压采用样品1.2倍的起始放电电压，采样电压采用稳定放电时的试验电压。采样电压和采样时间均因模型而异；试样均在工频条件下存储局部放电三个电压等级下150个单次放电波形。试验中需调节调幅电路的放电倍数，因此在每组试验结束后需按图3所示接线校正试验回路标定单位幅值的放电量，q0＝U0×C0其中U0是标定方波，C0是分度电容。

2 数据分析及处理

2.1 小波去噪

由于局部放电超高频信号是一种奇异性较强的非平稳信号。采用小波变换提取白噪声中局部放电脉冲信号比其它数字化滤波方法效果更好。为寻求最佳去噪结果，结合小波去噪仅去除白噪声不影响幅值的特点，本文采用波形相似系数（NCC）［12-13］描述去噪前后波形间差别以确定最优小波层数和小波尺度。其定义为：

式中s1为原始放电波形；s2为小波去噪后放电波形。波形相似系数的取值范围为［-1，1］，-1表示两放电波形反向；0表示两放电波形正交；1则表示两放电完全相同［11］。

通过大量计算并统计NCC值选取各放电模型去噪小波层数和小波尺度最优值（选取范围dept＝3～9，db＝1～10）。因数据量大本文仅列出11 kV下油中电晕放电一个单次波形的NCC值和三个电压等级下4种放电模型的小波去噪参数最优选取值，详见表1、表2所示。

表1 11 kV下油中电晕放电一个单次放电波形的NCC值Tab.1 NCC of a single PD waveform for oil corona discharge under 11 kV

表2 各电压等级下四种放电模型的最优小波去噪参数Tab.2 The optimum wavelet de-noising parameters of 4 kinds of PD models under different voltage levels

2.2 超高频信号特征量提取

本文通过对小波去噪前后局部放电超高频信号分别进行小波包多尺度变换，提取多尺度小波系数的网格维数和能量参数组成两个综合特征矩阵，反映各放电模型局部放电特征［13-14］。据表2参数对局放超高频信号去噪后，将去噪前后局部放电超高频信号分别进行多尺度小波包分解，采用改进差盒计数法［10］计算多尺度分解系数的网格维数。计算方法如下：

对二维分形曲线y＝f（x），用尺度为r的网格覆盖分形曲线，所需网格数为Nr需满足：

式中D为网格维数即分形曲线的分维数。改进DBC用一个网格状栅格来覆盖分形曲线，栅格的尺度定义为r。若第i个栅格内曲线段最小值与最大值分别为 fmin（i）和 fmax（i），覆盖该曲线段的网格数 Nr可得。

式中r′＝r／L；L为曲线的采样点个数。则覆盖全部分形曲线的网格数为：

计算出对应于不同尺度r的Nr，求出log（Nr）-log（r）拟合直线的斜率，其负数为分形曲线 y＝f（x）的网格维数。本文分形曲线为多尺度小波系数与小波系数个数的关系曲线。

其次，计算多尺度能量系数。方法如下：

假设被测信号 s＝｛si：i＝1，2，…，n｝经小波包分解后的全部系数为 c＝｛ci：i＝1，2，…，n｝，其总能量为：

任意分解空间的系数 ak＝｛akj：j＝1，2，…，n1｝的能量为：

则该分解空间的多尺度能量参数定义为：

信号N层小波包分解后的多尺度能量参数的向量为 E＝｛Ek：k＝1，2，…，2N｝且多尺度能量参数向量中各参数已归一化；多尺度网格维数的向量为D＝｛Dk：k＝1，2，…，2N｝。二维曲线的网格维数在 （1，2）之间。则对多尺度网格维数向量中参数进行归一化计算即求实际网格维数与1间差值。多尺度能量参数向量与网格维数向量构成局部放电超高频信号的归一化特征向量。参考小波去噪时小波尺度和小波层数的选取原则，经统计选取Dept＝4，db8时聚类效果和模型识别最优。表3为四层小波包分解多尺度特征参量与对应频带。

表3 局部放电超高频信号四层小波包分解多尺度特征参量Tab.3 Multi-scale characteristic parameters of PD UHF signals using 4-layer wavelet packet decomposition

3 模糊C-均值聚类算法

为验证超高频特征参量能有效表征油纸绝缘4种放电类型，本文采用模糊C-均值聚类算法（Fuzzy C-Means algorithm，简称为 FCM）［15-17］，分别对局部放电样本数据的32个特征量进行聚类分析及识别。

模糊C-均值聚类算法建立起样本对类别的不确定性的描述。FCM算法的c个模糊组由n个数据的向量集 X＝｛x1，x2，…，xn｝组成，在非相似性指标的价值函数最小的前提下，计算每组的聚类中心。FCM聚类算法的目标函数为：

式中 V＝｛v1，v2，…，vc｝是聚类中心向量；U＝［uik］c＜n是隶属度矩阵。对于任意 k（1≤k≤n），隶属度矩阵需满足以下条件：

式（8）中，uik为 xk属于第 i类的隶属度；dik＝‖xk-vi‖2是样本第i类中心向量vi与xk的欧几里德距离；m是模糊度权重，取值区间为［1，∞），它影响模糊隶属度矩阵的模糊度。FCM聚类算法步骤如下：

（1）选定需聚类个数 c（2≤c＜n），模糊度权重m，最大迭代次数 tmax和容许误差 ε（0＜ε＜1），随机产生初始化模糊隶属度矩阵 U（0）＝［uik］c＜n；

（2）按照公式（11）计算 V（k）；

（3）按照式（12）修正模糊隶属度矩阵即计算 U（k+1）；

（4）若满足聚类终止条件‖U（k+1）-U（k）‖ ＜ε或迭代次数等于tmax，迭代计算结束，显示识别结果和识别时间。否则，令k＝k+1，返回至第2步重复进行计算。

FCM算法通过迭代计算来修正聚类中心，使得误差平方和目标函数最小。FCM算法采用拉格朗日乘数法，不依靠初始的聚类中心，是动态聚类算法。

4 识别结果分析

本文采用FCM算法对表征典型油纸绝缘缺陷的4种局部放电模型试样超高频样本特征参量进行聚类和识别。特征参量矩阵由超高频信号16个能量参数和16个网格维数组成。为验证初始聚类中心对结果无影响，每次随机选取聚类中心并连续进行聚类30次的条件下，比较FCM算法对4种放电模型超高频特征参量的识别效果。参考文献［12］FCM参数选取m＝2并在同参数下运行30次并获取识别率。

由表4可知，对去噪前4种放电信号特征参量的识别平均值均高于65%，证明本文所采用的算法适用于该数据类型且FCM算法能正确识别4种局部放电类型；对比表4、表5去噪前后识别效果，识别率存在微小波动，各放电模型的识别率平均值均远高于去噪前，充分表明小波去噪能够有效提高正确识别率；小波包多尺度超高频网格维数和能量参数能够有效表征4种放电模型特性。

表4 去噪前信号特征参量识别率Tab.4 Recognition ratios of characteristic vectors before de-noising signals

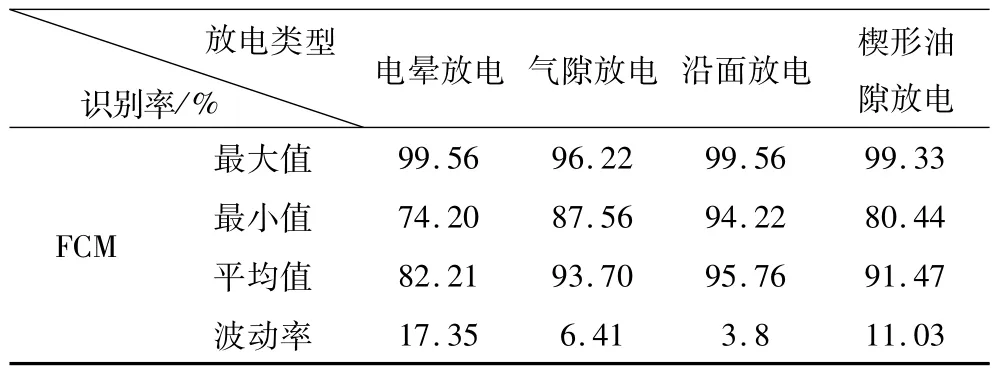
表5 去噪后信号特征参量识别率比较Tab.5 Recognition ratios comparison of characteristic vectors after de-noising signals

对比分析表5、表6可知，小波去噪后FCM算法的特性指标：正确识别率、最小识别率、识别稳定性和收敛性均明显高于去噪前算法识别结果。小波去噪有效提高了FCM算法的识别率和识别稳定性。结合模糊聚类不需要训练样本和直接通过学习实现自动分类的特点综合进行分析，小波去噪优化了FCM算法的对超高频信号的识别和在线应用。

表6 去噪前后算法特性指标Tab.6 Characteristic indexes of both algorithms with and without de-noising

5 结束语

为有效识别电力变压器油纸绝缘缺陷、评估绝缘状态，结合局部放电信号能较好反映变压器内部绝缘状况的特点。本文通过引入小波算法对局部放电超高频信号进行去噪的方法，研究FCM算法诊断油纸绝缘缺陷方法的适用性，得出以下结论：

（1）针对变压器绝缘内部放电形式和特点，有效模拟变压器油纸绝缘缺陷，确保试验与放电模型的一致性，搭建4种典型油纸绝缘局部放电模型，并提取局放超高频样本数据；

（2）选取最优小波参量对超高频信号进行去噪，分别提取去噪前后信号小波包多尺度16个能量参数和16个网格维数组成的两个综合识别矩阵；对比去噪前后识别结果表明，小波去噪能够有效提高模糊聚类算法的正确识别率、最小识别率、识别稳定性、算法稳定性和收敛性；验证了超高频信号小波包多尺度能量参数和网格维数能有效表征四种局部放电模型特性；

（3）FCM算法通过迭代计算修正聚类中心，使误差平方和目标函数达到最小。对比四种局部放电模型去噪前后特征参量识别结果。结果表明，模糊C-均值聚类算法能对局部放电超高频未去噪信号进行有效分类，验证了模糊算法对油纸绝缘缺陷识别的适用性。为局部放电超高频信号特征参量有效应用于油纸绝缘系统状态诊断提供依据，并为拓展变压器寿命预测和状态评估理论奠定基础。