基于自适应多尺度形态学和CEEMD的谐振接地故障选线研究*

陈奎，杨炼，王洪寅，万新强

（1.中国矿业大学 信息与电气工程学院，江苏 徐州221008；2.江苏省宿迁供电公司，江苏宿迁223820）

0 引 言

小电流接地电网中，最易发生的单相接地故障发生率远远超过其他故障，由于故障电流小、接地系统的复杂性、零序电流互感器特性的影响、谐波分量的影响、中性点接地方式的不同和测量精度的影响，导致接地故障选线困难，谐振接地时更是如此。消弧线圈的接入虽然使接地电流显著减小，但是引起了故障特征不明显，给选线带来了许多困难。

目前国内外选线方法基本分为暂态法和稳态法。与稳态法相比，暂态故障的特征量要大十几倍到几十倍，因此学者们对于暂态法的研究更为关注。常用的暂态信号特征提取方法有：暂态能量法、数学形态学、相关分析法、小波分析、Prony算法、经验模态分解等。利用暂态能量法进行选线，由于消弧线圈的补偿，造成各线路故障电流很小，容易造成选线装置误判［1］。数学形态学在图像处理和非线性滤波时具有很好的效果，选择合适的结构元素是滤波处理关键所在［2］。相关分析法，当接地电阻很大时，其准确度难以保证［3］。小波分析的小波基函数难以选择，其对选线准确性有很大影响，而且不具有自适应性，一旦分解尺度和小波基确定了，它的分析效果与分辨率就是一定的［4］。Prony对噪声十分敏感，极易受到噪声的干扰，算法在模型阶次的确定上的问题也还没有得到很好的解决，而且它对高频信号的拟合效果不行［5］。EMD具有良好的时频特性和自适应性，然而其端点效应和模态混叠可能会导致结果严重失真［6］。

基于上述问题，针对小电流谐振接地故障选线问题，提出了自适应多尺度复合形态滤波和CEEMD相结合的选线方法，不仅克服了小波变换时小波基选择困难的问题，还改善了一般形态滤波器的滤波效果并解决了EMD的模态混叠问题。

1 形态学滤波［7］

1.1 形态学基本原理

数学形态学是一种基于随机集和积分几何的处理分析非线性信号的工具，这种方法首先通过逐个考察信号各部分间的关系并进行检验，然后得到信号各部分之间关系的集合，最后确定信号结构。电力系统信号分析只涉及到一维信号，所以此处只介绍一维离散情况下的形态变换。

定义1：设 ()f x为定义在Zn上的离散函数，结构元素B为Zn上的有限子集，则四中基本形态变换定义如下：

f（x）关于B的腐蚀与膨胀运算分别为：

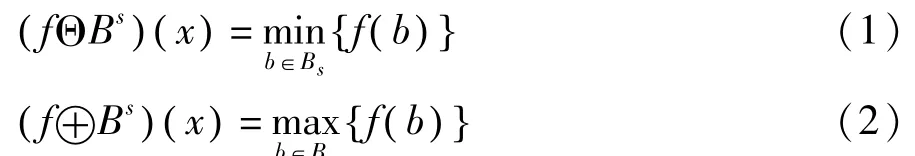
f（x）关于B的开运算和闭运算分别为：

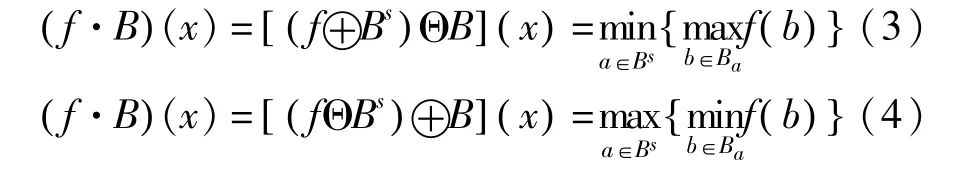
其中Bs＝{-b：b∈B}，即为B关于原点对称的集合；Bx＝{ b+x：b∈B，x∈ZN}，即为B关于点x的平移集合。

离散形式的腐蚀与膨胀运算相当于离散函数在滑动滤波窗内的最小值与最大值滤波。形态开闭运算有膨胀和腐蚀运算按不同顺序级联构成，开运算可以抑制或平滑信号的峰值噪声，闭运算可以抑制或平滑信号波谷的噪声。

1.2 自适应形态滤波

传统的形态开-闭和闭-开滤波器分别定义如下：

式中g为结构元素，它们通过不同级联的开闭运算构成，所以具有开闭运算的所有性质，然而却存在统计偏倚现象，并没有完全滤除脉冲噪声。

为解决上述问题，通过采用不同尺寸结构元素，构造广义开闭和闭开滤波器，定义分别如下：

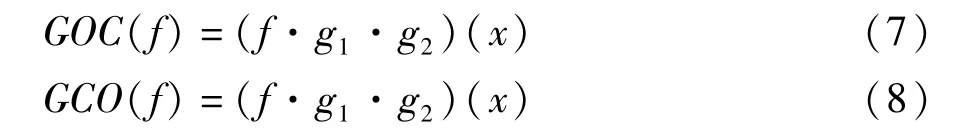
综合利用上述滤波器特点，有文献提出了自适应加权组合广义形态滤波器［8］，结构如图1所示。

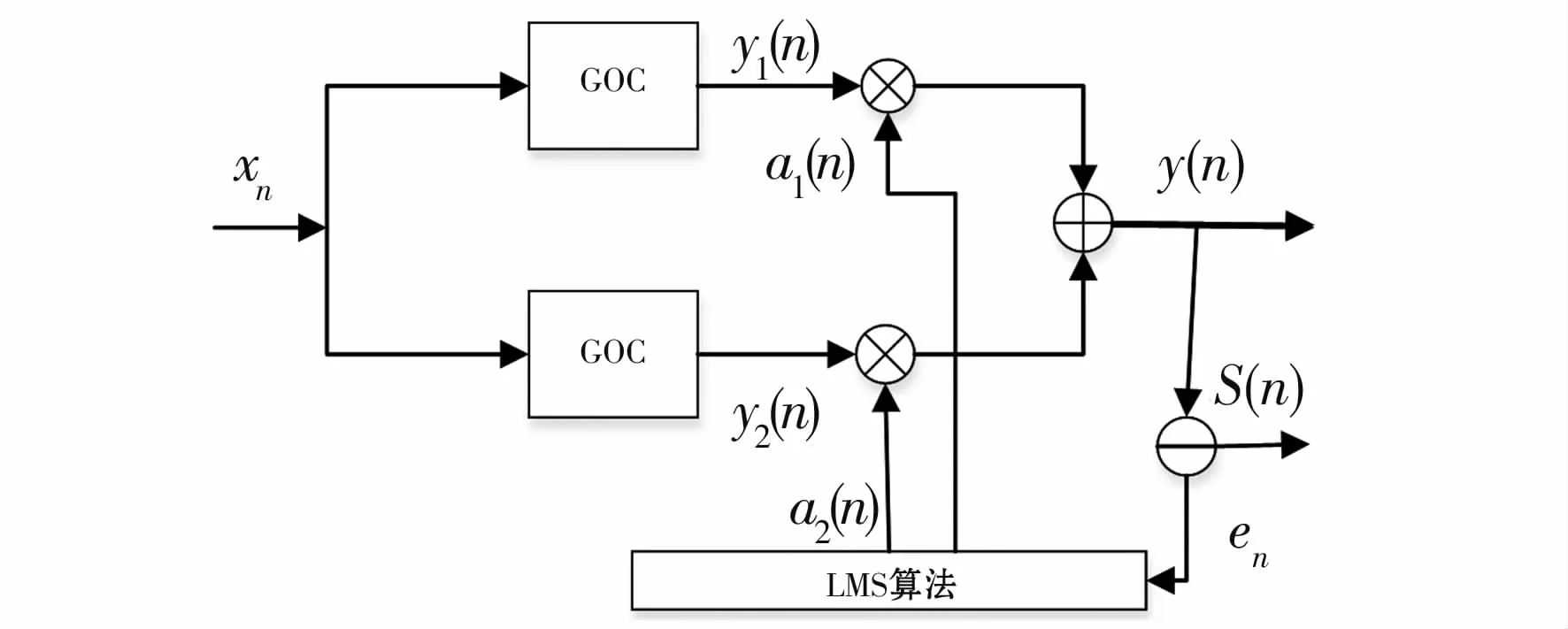
图1 自适应广义形态滤波器原理框图Fig.1 Principle block diagram of adaptive generalized morphological filter

其中输入信号 xn＝s0（n）+d（n），s0(n)为理性信号；dn为噪声；yn为滤波输出信号；sn是期望响应；en是误差信号；输出 y( n)＝a1(n) y1(n)+a2(n)·y2(n)。自适应形态滤波器的核心算法就是最小均方算法即LMS算法，权系数 ［a1（n），a2（n）］的调整完全依靠于这种算法，最后使得输出信号更接近理想值。

1.3 多尺度形态学分析

运用多尺度形态学分析［9］得到的结果往往只反映当前尺度下的有用信息，因此使用不同尺度的结构元素进行滤波更加有利于全面消除噪声干扰。自适应多尺度形态滤波的主要思想是利用大小不同的结构元素来提取信号信息特征，大尺度的结构元素的去噪能力较强，然而信号的边界会更加模糊：小尺度的结构元素去噪能力弱，但是信号的细节信息能够得到很好的保留。所以将不同尺度的信号结合起来可以实现更好的滤波效果。

结构元素的形状与大小对形态变换运算会产生很大的影响，相对而言，结构元素越复杂其滤除信号的噪声的能力就越强，越接近原始信号形状，则滤波效果就越好。综合以上考虑，本文采用了多尺度半圆形和三角型的结构元素进行自适应形态学滤波，有利于消除噪声干扰，同时尽量保留原始信号特征，减小失真。

在实际的电力系统配电网中往往存在由电磁干扰产生的一定强度的脉冲噪声以及其他外界因素产生的随机噪声，因此本文决定在原始信号加入幅值为5的正负脉冲干扰和标准差为0.1的随机噪声，假设原始信号为 x( t)＝sin( 2 π×50t)+sin( 2 π×100t)，采样点数为200，频率是1 kHz。图2～图4为传统（仅用单位三角形元素）和自适应多尺度形态滤波效果比较分析图。

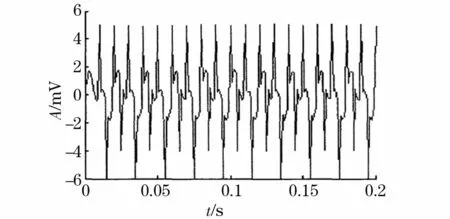
图2 加入噪声后的波形Fig.2 Waveform after adding the noise

图3 传统形态滤波后的波形Fig.3 Traditionalmorphological filtered waveforms

图4 自适应多尺度形态滤波后的波形Fig.4 Adaptivemultiscalemorphological filtering waveform

从上述波形图可以看出，传统形态滤波结果的波峰及波谷出现失真且存在一些畸变，而自适应多尺度形态学滤波却基本体现原始信号大致波形，且脉冲噪声得到了消除其效果要明显比前者好得多。

2 改进的HHT算法

2.1 互补集合经验模态分解

对于固有模态函数，可以用HHT变换构造解析信号，接着可以求出瞬时频率；对于不满足固有摸态函数条件的复杂信号，先要采用EMD方法将其分解［10］。任何复杂的信号都是由一些不同的固有模态函数组成，每一个固有模态函数无论是线性还是非线性、非平稳的，都具有相同数量的极值点和过零点，在相邻的两个过零点间只有一个极值点，而且上下包络线关于时间轴局部对称，任何两个模态之间是相互独立的［11-12］。

在上面条件的基础上，可采用EMD方法通过图5中的步骤对信号进行分解。由于上述假设条件，所以这种方法本身也存在着缺陷，这些问题主要集中在端点效应、模态混叠、筛分准则的确定以及样条拟合等方面。

本文通过CEEMD方法，利用成对添加白噪声来保证信号的完备性，使得分解结果很彻底，与EMD和EEMD相比，其使得模态混叠效应减轻了，添加噪声的集成次数也减小了，克服了能量泄露现象，同时还减少了虚假分量，而且还极大地提高了计算效率。具体步骤如下：

（1）在原始信号里成对地添加符号相反、大小相同的白噪声；

（2）利用前文所述的EMD方法分解添加白噪声后的信号，然后可以得到IMF分量；

（3）重复添加不同噪声，再进行EMD分解；

（4）对所有得到的IMF分量取平均值，得到最后的分解结果。

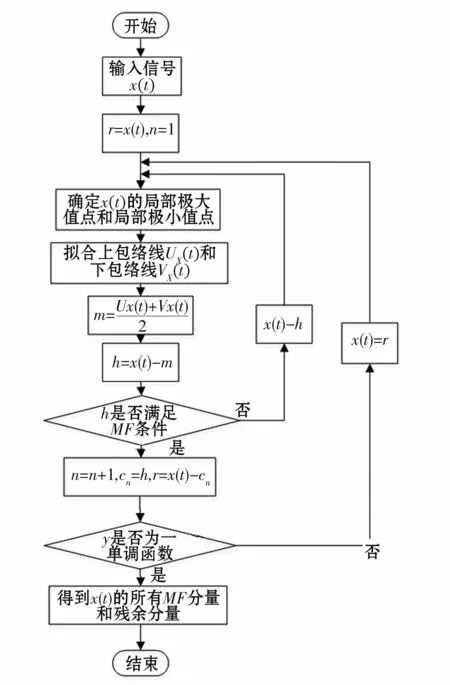
图5 EMD算法流程图Fig.5 Flow chart for EMD algorithm

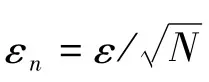
2.2 Hilbert变换

首先对N个IMF分量ci()t进行HHT变换得到：

构造解析信号：

其幅值函数为：

相位函数为：

瞬时频率为：

省略rn，那么原信号可以表示为：

上式即为原始信号的Hilbert谱分析［14］。

3 仿真分析

为了降低倒相和电流互感器饱和对选线结果的影响，本文决定选取故障发生前后各十分之一周期的零序电流进行CEEMD分解分析。三馈线的供配电系统原理图如图1所示，该系统采用过补偿方式，过补偿度为5%，经计算消弧线圈电感 L＝0.869 7 H，R＝30Ω。在MATLAB仿真中，线路的正序参数为：R1＝0.012 73Ω／km，L1＝9.337×10-4H／km，C1＝1.274×10-8F／km；零序参数为 R0＝0.386 3Ω／km；L0＝4.126 4×10-3H／km，C0＝7.751×10-9F／km。模型中线路长度分别为103 km、175 km、151 km。电源采用的是“Three-phase source”模型，电源功率为10 000 MVA，电压是110 kV，输出电压为11 kV。变压器额定容量为Sn＝20 MVA，短路电压Us%＝10.5，短路损耗ΔPs＝135 kW，空载损耗 ΔP0＝22 kW，空载电流 I0＝0.8，变比 Kt＝110／10，高低压绕组均为Y型联结。线路负荷均采用“Threephase Series RLC Load”模型，有功负荷分别为1 MW、0.2 MW、2 MW，仿真中的采样频率设为100 kHz，初始故障时间先设为0.04 s。系统仿真模型如图6所示。

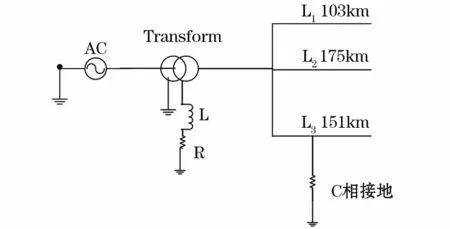
图6 仿真模型Fig.6 Simulation model

电力系统故障暂态信号中往往含有多种类型的噪声，而且各种噪声在成分和结构上也有很多不同点，非故障线路信号中可能存在与故障信号相似的突变量以及高频的电流分量，这些都能影响选线的准确度。因此为了更加有效地提取零序电流中的特征信号，必须对零序电流进行一定的滤波处理，抑制噪声对选线结果的干扰。

在对信号进行自适应多尺度形态学滤波后，再将处理后的信号进行CEEMD分解，根据上述原理可以得到多个IMF分量和一个残余分量。限于篇幅，文中只给出过渡电阻Rf＝0，故障时间t＝0.04 s时的故障线路L3和一条非故障线路L1的部分CEEMD分解结果波形图。

从图7和图8的CEEMD波形可以看出，随着分解过程的深入进行，得到的 IMF包含的振荡频率也会变得越来越低。

图7 L1的CEEMD分解波形Fig.7 CEEMD decomposition waveform of L1

图8 L3 CEEMD分解波形Fig.8 CEEMD decomposition waveform of L3

根据图9中L1、L2和L3的相位波形可以看出，经过CEEMD分解后的零序电流信号的相位在故障线路与非故障线路的相位存在一定的差异，对此，本文利用第一个高频CEEMD分量IMF1的相位关系得到选线判据。设各馈线处理后的信号在故障时刻的相角信息分别为 θ1、θ2、θ3，如果满足式（15），就可以判断出线路L1出现故障：

若满足式（16），则判断是母线故障：

在另外一方面，由于故障线路和非故障线路在幅值大小上存在差距，所以相角有时可能不满足上述关系，因此仅凭相位关系来进行选线判断很可能造成错误选线，为此还需要其他选线方法来弥补其不足之处［15］。另外，从上述图形可以看出，非故障线路与故障线路在故障后的1／4周期相位相差180°。由此，可以通过信号的极性来判断故障线路。本文还通过提取CEEMD的奇异点信息特征来实现上述极性判断的。

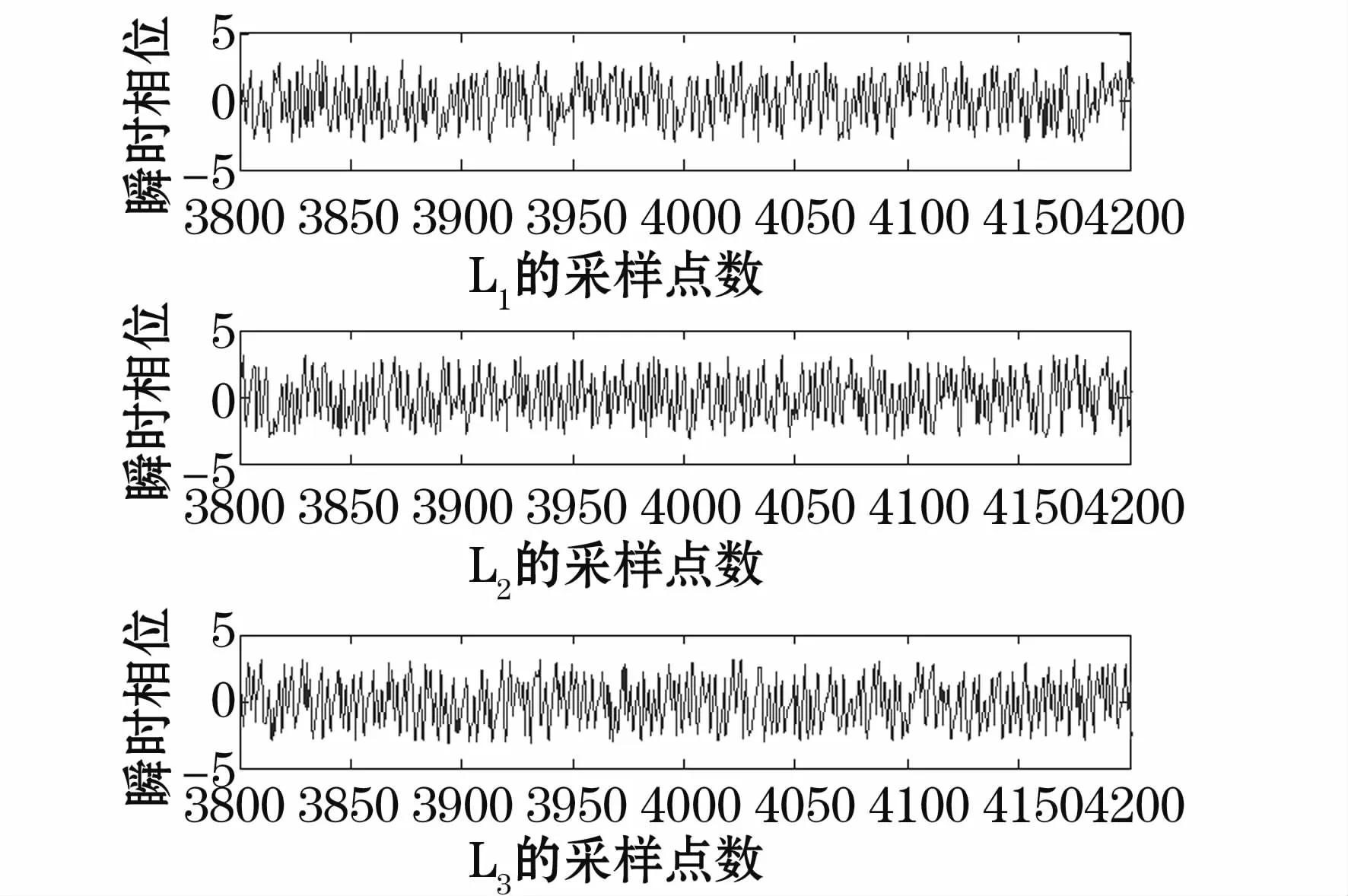
图9 所有线路的IMF1的HHT变换波形Fig.9 The HHT transform waveform of all transmission lines IMF1

4 选线机制

信号的突变可以体现在CEEMD分解得到的每个IMF分量中。由于这种方法的时频分辨率随着频率升高而增加，所以本文中利用高频分量来提取零序电流的奇异信息，即提取分解后的第一个IMF分量来进行故障选线分析。由于信号中的突变点的局部尺度很小，所以本文根据相邻极值点的间隔与极值差大小来实现上述的幅值与极性判断，利用一阶差分即可得到可靠选线判据［16］。

基于上述分析，本文选用的是一种自适应多尺度形态学与CEEMD结合的故障选线方法。根据小电流接地系统故障后，在暂态过程时，非故障线路与故障线路的电流相位与幅值都有差别，本文对故障前后1／10周期的电流信号进行数字信号处理，然后根据个馈线奇异点的一阶差分符号和大小来进行选线。故障选线算法详细流程如下：

（1）利用自适应多尺度多结构元素复合形态学对故障时收集的零序电流波形进行滤波处理；

（2）采用互补集合经验模态分解（CEEMD）方法对滤波后的故障发生前后1／10的信号进行分解处理，得到多个IMF分量和1个残余量；

（3）对所选取的高频IMF第一个分量的信号进行奇异性检测并进行HHT变换，确定奇异突变点且得到瞬时相位波形图；

（4）对第一个IMF分量进行一阶差分，然后计算奇异点处的结果，接着计算故障时刻的相位；

（5）若一条线路在故障时刻的相位与其他线路的相位差均大于90°且一阶差分值与其他线路相反，判断为故障线路，若不满足式且一阶差分相同，则判断为母线故障。以一阶差分极性为主要判据，相角为辅助判据。

5 算例分析

针对小电流单相经消弧线圈接地故障进行了大量仿真计算，实验研究了不同情况下的故障初始角、故障位置和过渡电阻对选线结果的影响。故障选线结果如表1所示，根据表中的数据可知，本文所提出的方法在不同故障初始角、不同位置和不同过渡电阻大小时均能正确选线。

表1 实验结果Tab.1 Experiment results

6 结束语

详细介绍了一种基于自适应多尺度复合形态滤波和CEEMD分解的配电网故障选线方法。通过多尺度多结构元素复合的形态学滤波器，能有效去除原始信号中含有的噪声干扰。本文采集数据选为故障前后十分之一的数据，这样能够克服电流互感器在单相故障1／4后容易饱和的缺点，同时通过提取最高频的IMF分量，保持暂态过程主要成分的信息，提高了选线精度。经过多次实验，可发现算法的选线正确率很高，本方法拓展了配电网选线的新思路。