基于小波和高阶PDE的电缆局部放电去噪研究
汪培培,莫付江,赵岗岗,陈惠,许梦素
(江苏大学 电气信息工程学院,江苏 镇江212000)
0 引 言
随着电力电缆线路在城市电网中广泛应用,其安全可靠性受到极大的重视。局部放电是反映电缆绝缘性能的重要表征,也是导致电力电缆绝缘故障的主要因素。因此,对电力电缆的局部放电信号进行监测,能够及时发现故障隐患与准确掌握电缆绝缘状态[1-2]。但是由于强烈的白噪声[3]、周期性窄带信号[4-5]以及随机脉冲信号等外部干扰因素,导致检测出的PD信号出现严重波形畸变。近年来,国内外学者对局部放电的抑制研究最多的是小波变换的阀值去噪方法[6-8],它是根据小波分解获得的各层系数来选择一个阀值;然后对细节系数进行作用处理。但是阀值的选择是一个难点,从某种程度上,去噪的成功与否主要取决于阀值的选取。由于四阶PDE去噪不依赖阀值的选择,利用扩散系数针对不同的区域采取不同的扩散平滑策略,具有较强的自适应性,已在图像去噪[9]和振动信号提纯[10]方面展开了较多的应用研究。
提出了一种基于小波和高阶偏微分方程的电力电缆PD信号去噪方法。主要是将小波变换较好的预处理和后处理平台与四阶偏微分方程相结合对PD信号进行提纯,并与传统小波阀值去噪方法相比,实验成果显示,本文方法更能有效的提炼出真实的电缆PD信号,误差小且信号边缘细节保留较好。
1 高阶偏微分方程
1.1 PDE去噪模型
继PERONA等提出的经典P-M各向异性扩散方程之后,2000年,Yu-Li[12]等人提出了以下的四阶偏微分方程:
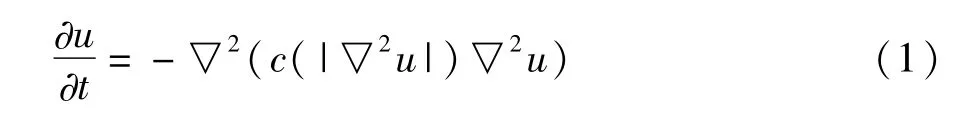
式中▽是哈密尔顿算子;▽2u是拉普拉斯算子;c(|▽2u|)是单调递减函数;c(|▽2u|)∈(0,1),具有如下性质:当|▽2u|→∞时,即在波形的边缘细节区域,c(|▽2u|)→0,扩散程度很小,从而保护波形的边缘细节;当|▽2u|→0时,即在波形的平坦区域,c(|▽2u|)→1,扩散程度较大,这样对于去除波形中的噪声非常有效。
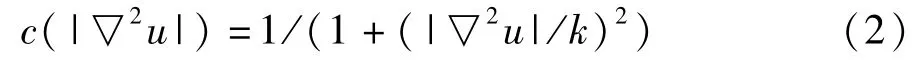
式中k表示迭代过程中的梯度阈值,当|▽2u|≤k时,函数扩散强度较大,可以抑制噪声;当|▽2u|>k时,扩散系数受到抑制,则起到保护波形边缘细节的目的。
1.2 方程的数值化
解式(2)对应的四阶PDE,就会达到对信号去噪的目的。将该偏微分方程进行简单的降维处理,就可以用于一维的PD信号去噪中来。令PDE中的变量 y为 0,重新令方程中的 u(x,y,t)=u(x,0,t),并记为u(x,t)即可。对该方程数值化,就可以迅速利用计算机软件编程求解,本文基于MATLAB进行编程。
对变量x和t划分网格,分别设H,τ,为空间步长和时间步长,令 xi=ih,tn=nτ,用平行于 x轴和 t轴的两组平行线建立网格。
依据微积分的基本原理:
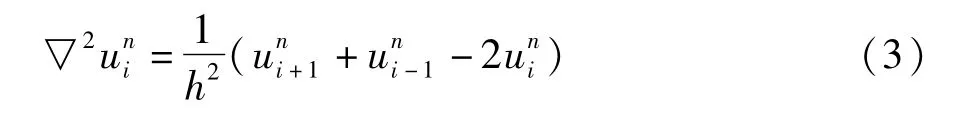
令 c(|▽2u|)▽2u=f(▽2u),则:

一方面:

另一方面:

依次将式(3)~式(5)代入式(6),就可以得到:

将含噪声的PD信号作为初始值,按照式(7)所给出的规律,依次迭代,顺序求出 u1i,u2i,…,u3i,经过合适的迭代次数,便可恢复出真实的PD信号。
2 最佳小波选择
选择合适的小波基对局部放电信号的预处理和后处理是至关重要的,目前采用最多的是相关系数法来选择最佳母小波[11]。即使含噪信号和各小波基之间的相关系数取最大值。相关系数表达式:
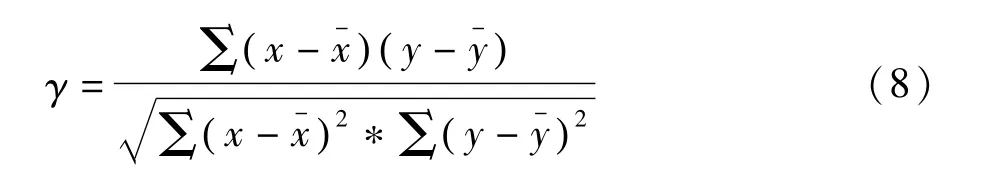
式中x表示噪声信号数据;y表示小波数据;x-与y-分别为x,y的平均值。利用式(8)计算出db系各阶小波和噪声信号的相关系数γ,所得结果如图1所示,可见db4小波基最为合适。
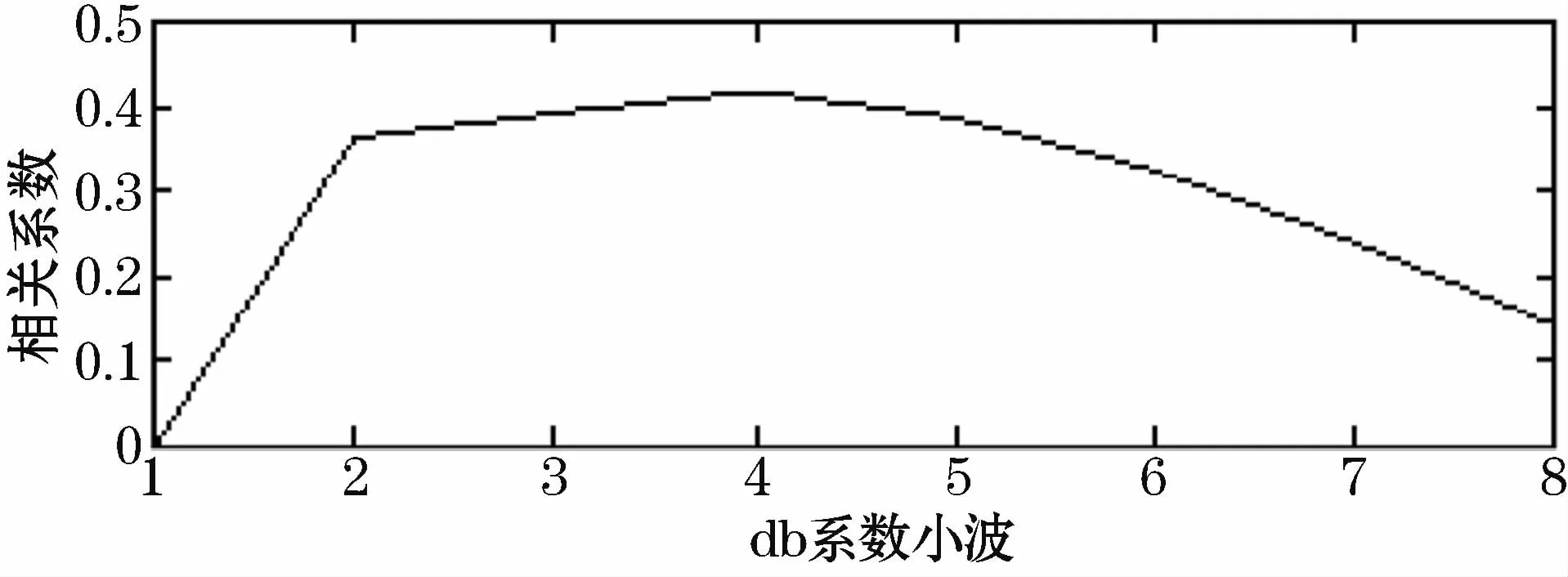
图1 db小波与PD信号相关系数Fig.1 Correlation coefficient of db wavelet and PD signal
3 基于小波和高阶PDE的去噪模型
本文结合了小波变换和高阶偏微分方程两种经典算法,具体的算法步骤是:
(1)首先输入采集到的局部放电噪声信号;
由于在设备运行监测中,存在大量噪声干扰,其中最主要的是白噪声和周期窄带干扰信号。因此,假定含噪信号为:

式中 s(t)是含噪信号;n(t)是白噪声信号;m(t)是周期窄带干扰信号;
(2)通过相关系数法选取合适的母小波,再选取合适的分解层数N,对采集到的噪声信号进行小波变换分解;
(3)对第N层低频子信号进行高阶PDE处理;
(4)计算去噪信号的信噪比SNR,重复步骤(3)、(4),直到某一次迭代输出的SNR值小于上一次迭代输出的SNR值,迭代终止;信噪比为:

式中powersignal表示PD信号的能量;powernoise表示噪声信号的能量;
(5)对第1层到第N层的各层高频子成分阈值处理;由于这些高频子成分含有信号的大部分噪声,主要局部放电信号很少,所以采用阈值处理可以使去噪后的波形相对平滑,不会出现较大的视觉失真,阈值k需要通过大量统计与分析得到;
(6)将低频子信号与高频子信号进行小波重构,获得去噪后的PD信号。整个去噪过程计算简单,运行速度快,能够更好地去除噪声且失真度较小,并较好地保留信号边缘。
4 PD信号去噪的仿真分析
PD信号的特点是幅值小,通常为毫伏级;持续时间短,通常为纳秒级;本文以常用的双(单)指数衰减模型、双(单)指数衰减振荡模型[13]为研究对象:

式(11)~式(14)中,α1和 α2是信号幅值系数;α1和α2为衰减常数;fc指振荡频率。图2给出了局部放电的原始信号,采样频率为2 000 MHz,时间以纳秒为单位。

图2 PD脉冲信号波形Fig.2 PD pulse signal waveform
由于大量噪声干扰的存在,使得检测到的PD信号已无法作为局部放电试验的依据,所以要模拟出被噪声污染的PD信号,上述已经给出了局部放电信号的数学模型,根据该数学模型,可以用MATLAB仿真出含有噪声的PD信号,在这里周期干扰信号m(t)取一个简单的正弦信号;此外,生成一个均值为0,的白噪声信号n(t),将这两种信号一起加入到p(t)中,仿真波形如图3所示。
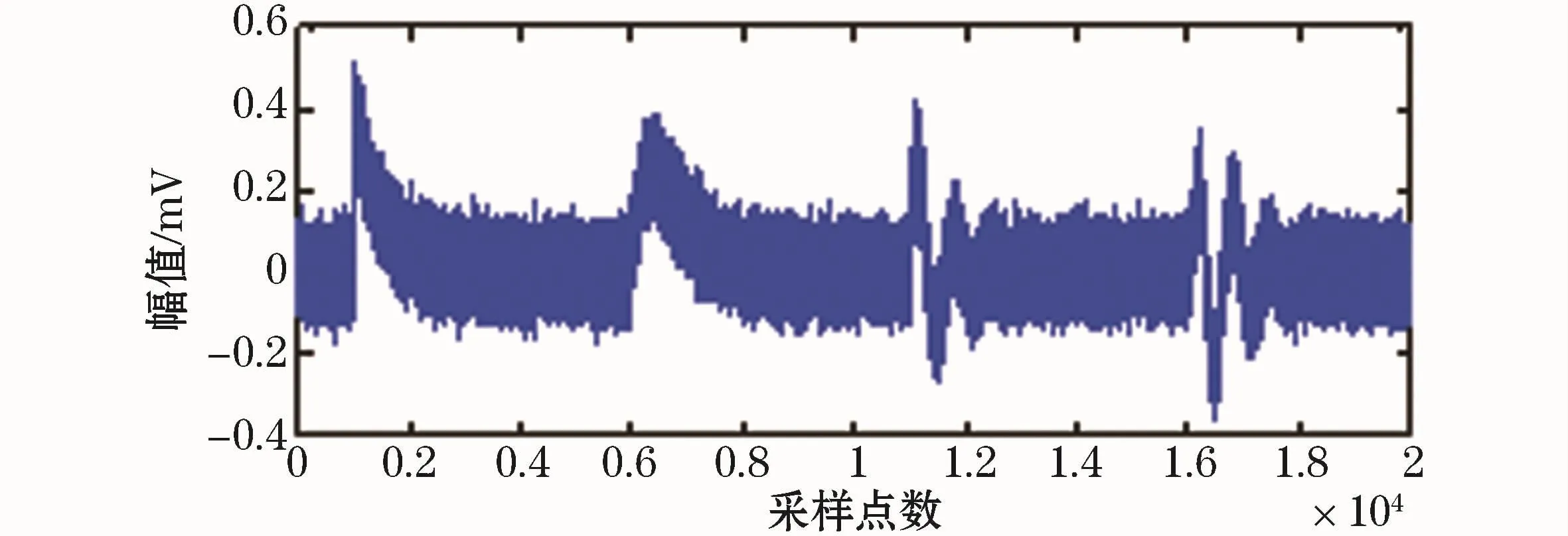
图3 含噪声的PD信号Fig.3 PD signal containing the noise
根据上述的去噪方法,采用db4小波基对含噪声的局部放电信号进行小波变换分解,分解为4层,如图4所示,低频子为 ca4,高频子依次为 cd4,cd3,cd2,cd1。

图4 小波分解的各尺度波形Fig.4 Scale waveform ofwavelet decomposition
从图4中可以发现,高频子成分含有信号的大部分噪声,而局部放电信号主要包含在低频子成分中。所以对第4层低频子ca4信号波形进行高阶PDE处理,迭代7次时,信噪比达到最大,迭代终止。同时采用传统小波分解阀值去噪方法对低频子ca4进行去噪处理,图5为两种方法去噪后的波形图,可以看出两种方法都能很好的去除噪声,但小波阀值去噪后波形的峰谷值较原信号明显缩小,局部波形畸变较大。
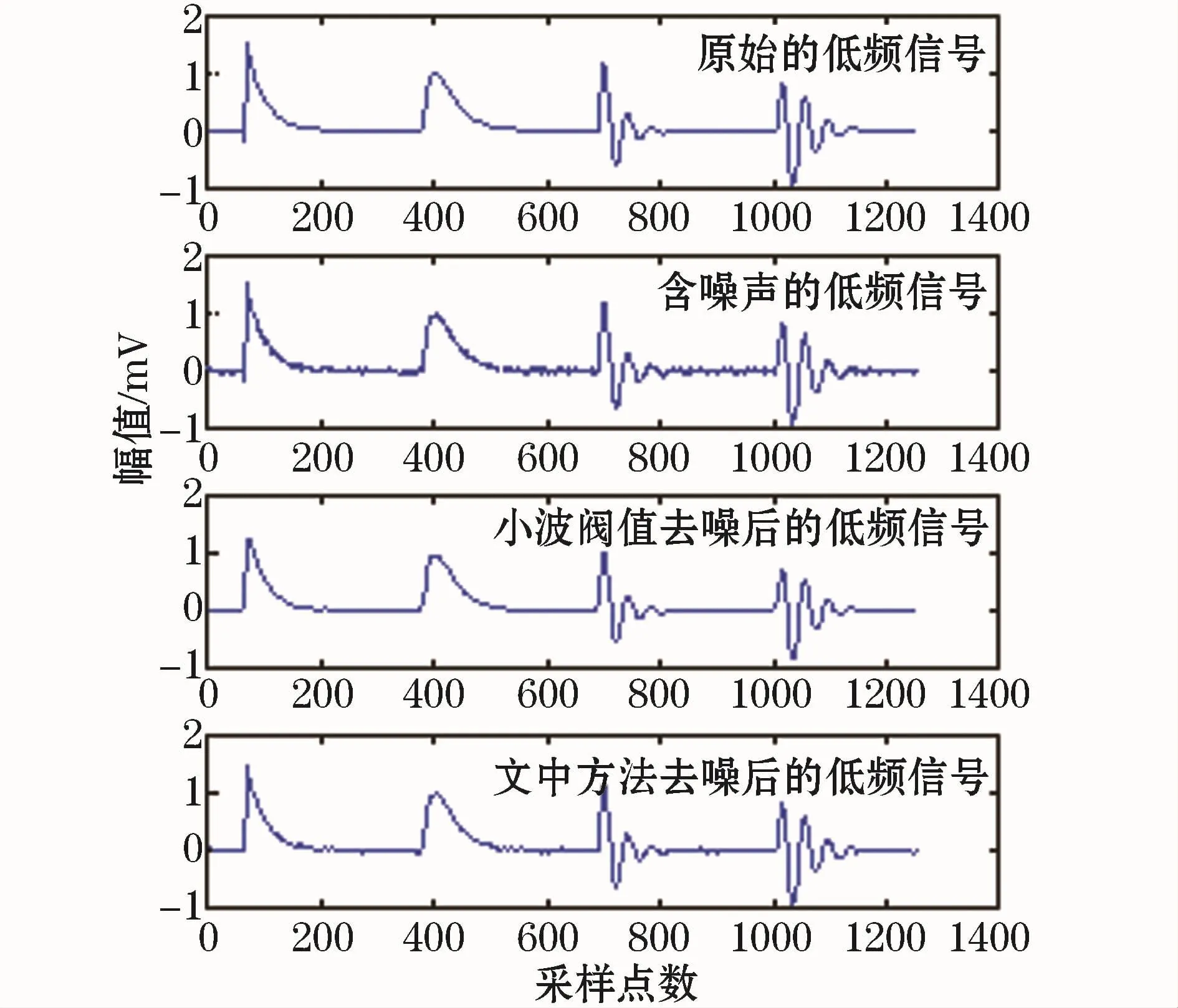
图5 低频子信号去噪前后的波形Fig.5 Waveform of low frequency signal before and after de-noising
将两种方法处理过的低频子信号与高频子信号进行小波重构,图6(a)为传统小波阀值去噪后的局部放电信号,图6(b)为结合小波和高阶PDE去噪后的局部放电信号波形。

图6 去噪后的PD信号波形Fig.6 PD signalwaveform after de-noising
从图6中可以看出两种方法都能基本去除噪声的干扰,但本文方法比较好地保留PD信号的边缘细节,畸变较小;而传统小波阀值去噪对信号的边缘细节部分过度抑制,从而导致信号峰值降低,局部放电信号波形畸变。结合两种方法去噪后的信噪比来看,如表1所示,文中方法去噪效果更佳优越一些,在信噪比上,基于小波的高阶PDE去噪方法要高于传统的小波阀值去噪。

表1 EVT试验情况简表Tab.1 EVT test conditions
表1中,S1为分解后的低频信号ca4;S2为重构后的整体PD信号。从表1中可以看出,SNR值并不是一直增大,而是先增大后减小,因此文中采用的迭代终止条件不仅提高了运行效率,还能防止波形失真,更有利于电力电缆故障分析。
5 结束语
文中利用小波变换较好的预处理和后处理平台,提出了小波与四阶偏微分方程相结合的电力电缆去噪方法,通过仿真研究,得出以下的结论:
(1)结合小波和四阶PDE对局部放电信号的去噪效果是十分明显的,从去噪后的PD信号波形可以看出,此方法可有效保留信号的边缘信息,且运算量较少,比其他传统小波阀值去噪方法更有利于真实的PD信号的快速提取;
(2)在采用四阶PDE迭代去噪的过程中,迭代次数并不是越多越好,实验表明,随着迭代次数的不断增大,SNR呈现先上升后下降的趋势,所以文章采用效果评价指数SNR作为迭代终止条件,可以使提炼出的信号更佳精确,波形畸变更小,以便于后续分析。

