基于下垂控制逆变器的虚拟发电机建模与特性研究*

司家荣，蔡国伟，孙正龙，任永平

（1.东北电力大学 电气工程学院，吉林 吉林132012；2.国家电网公司新疆电力科学研究院，乌鲁木齐830001）

0 引 言

近年来，为解决能源危机和缓解环境压力，风电、光伏发电等可再生能源发电技术飞速发展。分布式电源在电网比重越来越大，对电网经济性改善，运行方式的优化等方面有着积极的作用［1-3］。

分布式电源主要通过并网逆变器接入电网，跟传统的同步发电机相比，控制更加灵活、响应速度更快，但是缺点在于其阻尼不足和缺少惯性［4］。由于分布式电源比例的不断增加，传统的同步发电机装机比例将会减小，使得电力系统中转动惯量和旋转备用容量相对降低，这些不利于电网的安全运行。而且，分布式电源的并网逆变器的控制策略各不相同，电源输出的功率并不稳定，具有随机性和波动性，对电网稳定会产生不利的影响。如何通过有效合理的控制方法控制并网逆变器，将分布式电源安全可靠地接入电网成为研究的热点。

文献［5-6］中提出了并网逆变器联网时的下垂控制策略，可以使逆变器能够根据电网运行状态做出相应的调整，当电压或频率出现异常时能够及时作出响应，调整输出的有功功率和无功功率，从而改善电网的运行状态。但是下垂控制具有局限性，其只是模拟了同步发电机的下垂外特性，与同步发电机实际的运行特性还有差距。

要模拟同步发电机的真实运行特性，调速和励磁是两个重要的环节。文献［7-8］中从同步发电机的机械方程和电磁方程入手，在下垂控制基础上对并网逆变器的控制策略进行改进，使得并网逆变器在机理和外特性上更接近同步发电机，更好地模拟出同步发电机实际的运行特性，这种控制策略就是虚拟同步发电机（Virtual Synchronous Generator，VSG）技术。

虚拟同步发电机技术最早由欧洲学者提出，其本质上是一种应用在微电网控制领域的新型逆变电源［9］。目前，学者提出了多种虚拟同步发电机技术的实现思路。从控制策略上看主要分两类，一种是电流控制型，另一种是电压控制型。电流控制型的虚拟同步机相当于一个电流源，这种控制策略弊端明显，难以为电力系统提供电压和频率支持；电压控制型的虚拟同步机相当于一个电压源，其技术主要基于同步发电机机电暂态模型，模拟同步机的转子惯量和系统频率调整特性，实现频率的稳定性控制；而在电压调整方面，考虑无功-电压关系，实现对电压的稳定控制［4］。

基于VSG与同步发电机原理和结构的相似性，通过在Matlab／Simulink仿真平台中构建VSG的模型，根据其仿真运行特性，对现有控制策略的可行性进行验证。此外，通过仿真结果可对控制VSG运行的参数进行细致分析，为虚拟发电机高阶模型的搭建和励磁系统模型的完善提供帮助，为虚拟发电机技术今后在电网中的应用提供理论支持。

1 VSG的模型

1.1 VSG的原理

虚拟同步发电机（VSG）的原理是通过相应的控制策略来控制逆变器，模拟同步发电机的运行特性。其主电路结构如图1所示［4］。

图1 VSG主电路结构Fig.1 VSGmain circuit structure

图中，uabc＝［ua，ub，uc］T，iabc＝［ia，ib，ic］T，分别为VSG的三相输出电压和并网电流，ugabc＝［uga，ugb，ugc］T为电网侧三相电压，Udc为直流电压源，Ls为虚拟的同步电感。

由图1可知，VSG主要由两部分组成：主电路和控制单元。主电路与常规的并网逆变器结构相同，原动机用一个直流电压源代替、DC／AC变换器和滤波电路；而实现VSG的关键是控制单元，其中包括VSG的本体模型和控制算法，前者从机械运动及电磁角度模拟同步发电机，后者从有功调频和无功调压外特性上模拟同步发电机［10］。

如图2所示，VSG的控制单元通过控制算法来模拟同步发电机的运行特性。abc／dq为派克变换，将主电路中测量到逆变器侧电压和电流经派克变换，得到旋转dq坐标下的电压和电流d、q轴分量，θ为电角度；ma、mb、mc为经电流控制环得到的三相调制波。经测量装置得到电压电流瞬时值后，通过算法控制得到调制波，经过正弦脉宽调制（Sinusoidal PulseWidth Modulation，SPWM）生成脉冲信号控制开关管（IGBT）的通断。

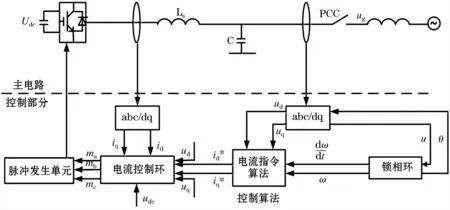
图2 VSG的控制单元Fig.2 Controlling unit of VSG

1.2 VSG本体模型

本体模型要根据同步发电机的阶次来建立，因此，不同阶次的发电机其VSG的建模也不同。国内外有学者提出用三阶、五阶等较高阶次的同步发电机模型来建立VSG本体模型，但是由于结构复杂，在实际应用中较难实现，所以本文采取发电机经典的两阶模型，主要由电磁部分与机械运动两部分组成。

电磁部分通过定子电压方程建模如下：

该模型忽略了定子电阻，只考虑了定子电路中电压-电流间的关系，但是并没有反映其中的磁链特性，所以存在一定缺陷。

针对这种情况，文献［8］中提出了新的模型：

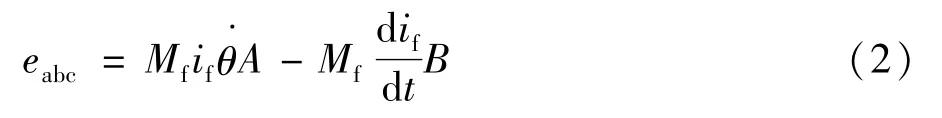
式中Mf为互感系数；if为励磁电流；θ为转子角度；A和B的定义如下：

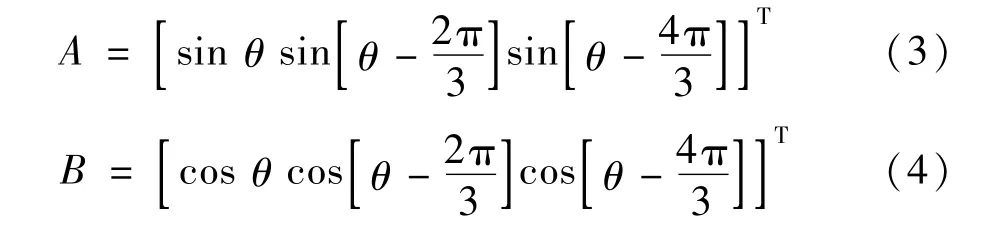
式（2）体现的模型考虑了同步发电机的电磁暂态特性，虚拟定子和转子之间的耦合度也得到体现，更准确的反映了同步发电机的运行特性［5］。

对于机械部分的建模，目前较为一致，利用转子运动方程，可得模型如下：

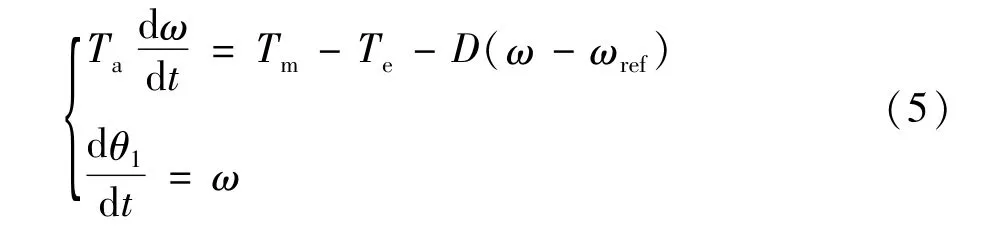
式中 Tm为机械转矩；Te为电磁转矩；ω为实际电角速度；ωref为额定电角速度；θ1为电角度；Ta为表征虚拟惯量的时间常数；D为阻尼系数。

VSG的阻尼特征和转子特性可以通过转子运动方程体现出来。由于反映转子转动惯量的机械时间常数的存在，使得VSG的动态过程中具有惯性；而阻尼系数D的存在使得VSG拥有阻尼功率振荡的能力［4］。

2 VSG控制系统的建模

2.1 有功-频率控制

同步发电机的频率与转子转速相关，由于其转子具有惯性，所以频率不会发生突变。VSG的控制算法中引入虚拟惯量来模拟同步发电机的转子运动特性，结合转子运动方程，可以得到有功-频率控制方程［7］：

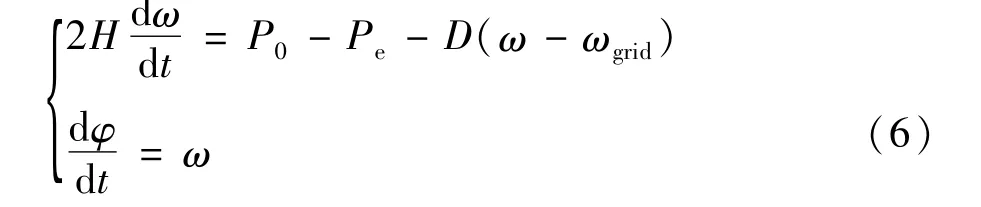
式中H为虚拟惯性时间常数；P0为逆变器有功功率给定值；Pe逆变器输出功率；D为阻尼系数；ω为逆变器侧角频率；ωgrid为电网侧角频率；φ为相位角。

当VSG并网运行在强电网时，其频率会被钳住在ωgrid，此时不需要VSG进行有功调频。如果在自治或孤岛模式运行时，就需要VSG能够进行有功调频［10］。通过模拟同步发电机的调速器，增加一个有功-频率下垂控制环节，可以模拟P-f的下垂特性：

式中ωref为角频率参考值；Dp为有功功率的下垂系数，反映了VSG的频率调节能力。

联立式（6）、式（7）可得：

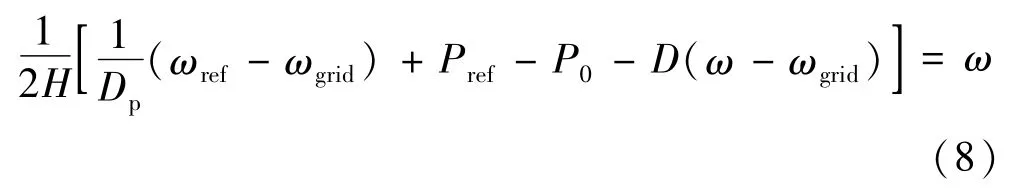
根据式（8）可建立有功-频率的控制框图，如图3所示。

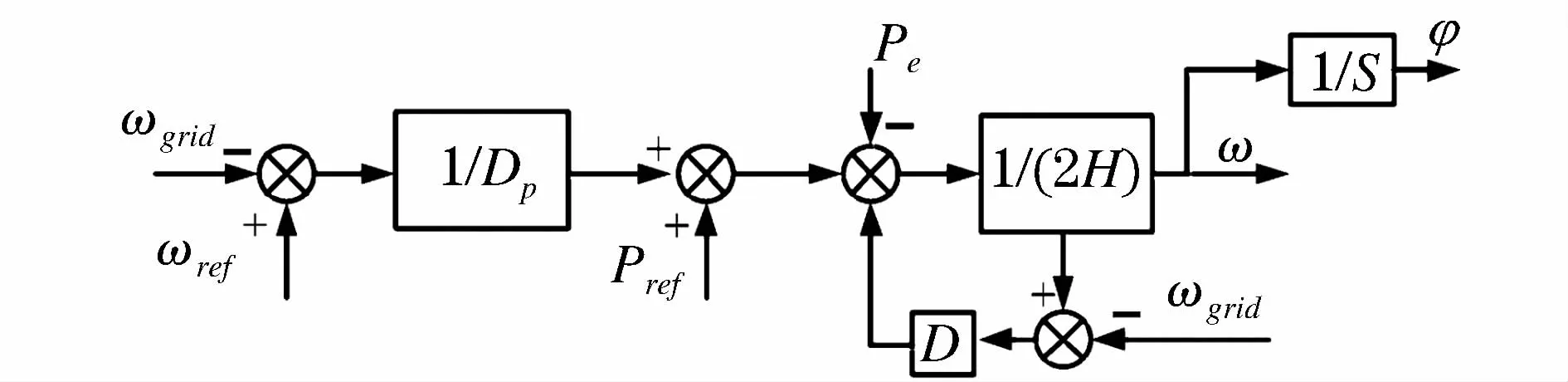
图3 有功-频率控制框图Fig.3 Active power-frequency control block diagram

当VSG工作在孤岛或自治模式时，阻尼部分D（ω-ωgrid）等于0，VSG的频率特性由下垂控制决定。

2.2 无功-电压控制

在同步发电机中，机组通过励磁系统来调节内电势，从而控制机端电压的稳定。而在VSG的无功-电压控制中，模拟同步发电机的励磁调节系统，用以维持并网点PCC电压稳定。

与有功-频率控制相似，VSG的无功-电压控制模拟实现无功功率和电压幅值的下垂特性，具体模型为［11］：

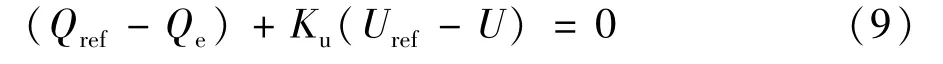
式中Uref为参考电压；U为并网点电压；Ku为无功功率的下垂系数，反映了VSG的电压调节能力。

图4为VSG无功-电压控制框图，其中K为积分系数；E为经过该控制得到的参考电压值。在实际应用中，可以将E与有功-频率控制得到的角度φ结合，得到参考电压的矢量表达。

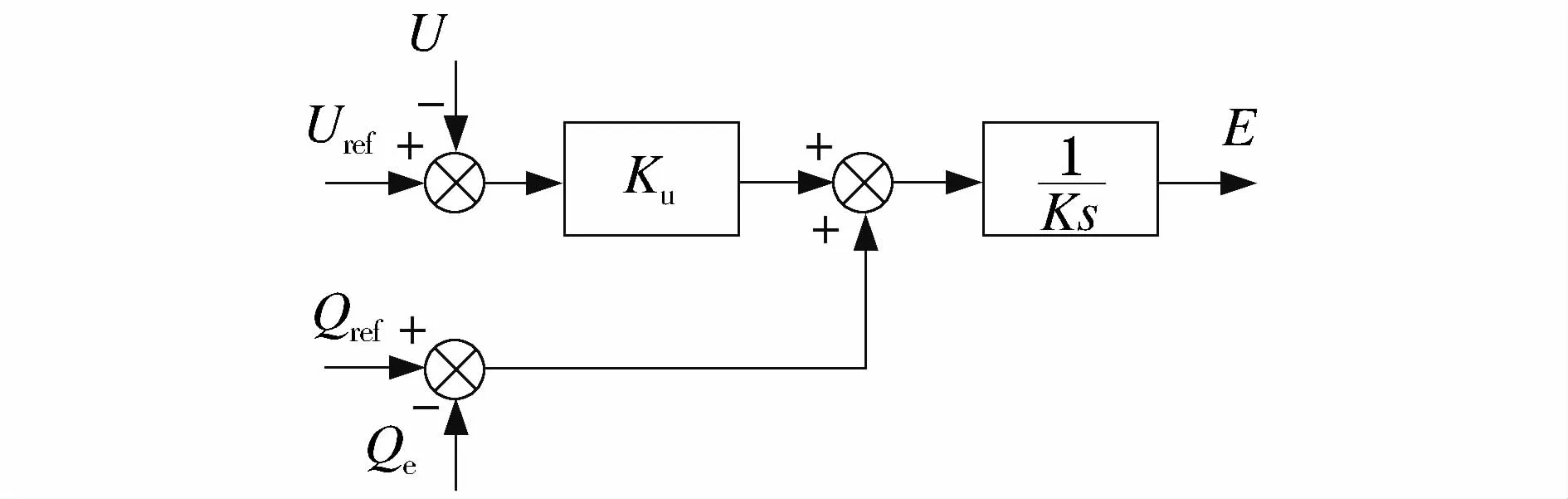
图4 无功-电压控制框图Fig.4 Reactive power-voltage control block diagram

在实际运行中，无功-电压的控制往往要比有功-频率的控制更加复杂。负荷变化、输电线路参数甚至是小的扰动都可能造成结果偏离控制，使得无功功率分配不合理。

针对以上问题，国内外学者也提出了相应的解决办法，有电压自恢复、利用虚拟阻抗减小电压降落、下垂参数自适应等改进的下垂控制方法［12-13］。

3 VSG并网稳定性分析

虚拟同步发电机VSG并网后，需要对其稳定性进行分析。由于VSG引入了虚拟转动惯量J和阻尼系数D，故与传统同步发电机静态稳定性分析方法类似，以单机无穷大系统为例，采用李雅普诺夫第一法（小干扰法）来分析［14］。

首先确定VSG的电磁功率表达式：

式中E为VSG逆变器输出电势；Ug为电网侧电压；X∑为逆变器到电网侧之间的电抗和；δ为E与Ug之间相位差。

其次将状态量在原来的运行情况上叠加一个小的偏移，此时状态量变为：

带入状态方程后，得其矩阵形式：

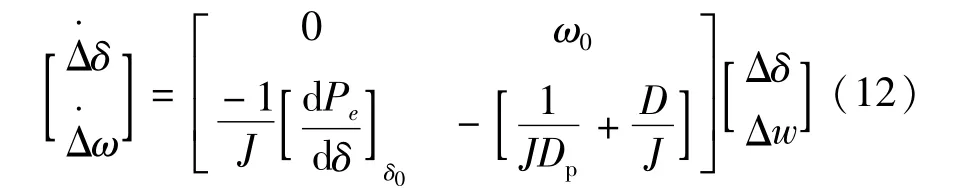
根据李雅普诺夫小干扰稳定性判断原则，若该系数矩阵所有特征值的实部均为负值，则系统是稳定的［15］。

文献［16］中提到：当有功功率设置为20 kW，无功率设置为0 kvar，Ls为2mH时，VSG的逆变器电势和其功角的稳定运行点为：Es＝314.13 V，δs＝0.063 rad。

式（13）为VSG在稳定运行点的比整步功率，虚拟转动惯量J、阻尼系数D以及有功功率下垂系数Dp对VSG稳定性都有影响。J越大，动态响应过程中的振荡频率越小，响应速度越慢，不利于系统的稳定；D越大，系统振荡衰减越快，有利于系统的稳定；Dp越大，系统振荡衰减越慢，不利于系统的稳定［17］。

4 仿真分析

虚拟同步机与下垂控制逆变器具有相似性，文献［18］中提到：虚拟同步发电机可以视为带有虚拟惯性的下垂控制器。所以在仿真时需针对虚拟惯性进行必要的控制，结合传统同步发电机的摇摆方程，可得虚拟惯性控制框图［19］，如图5所示。

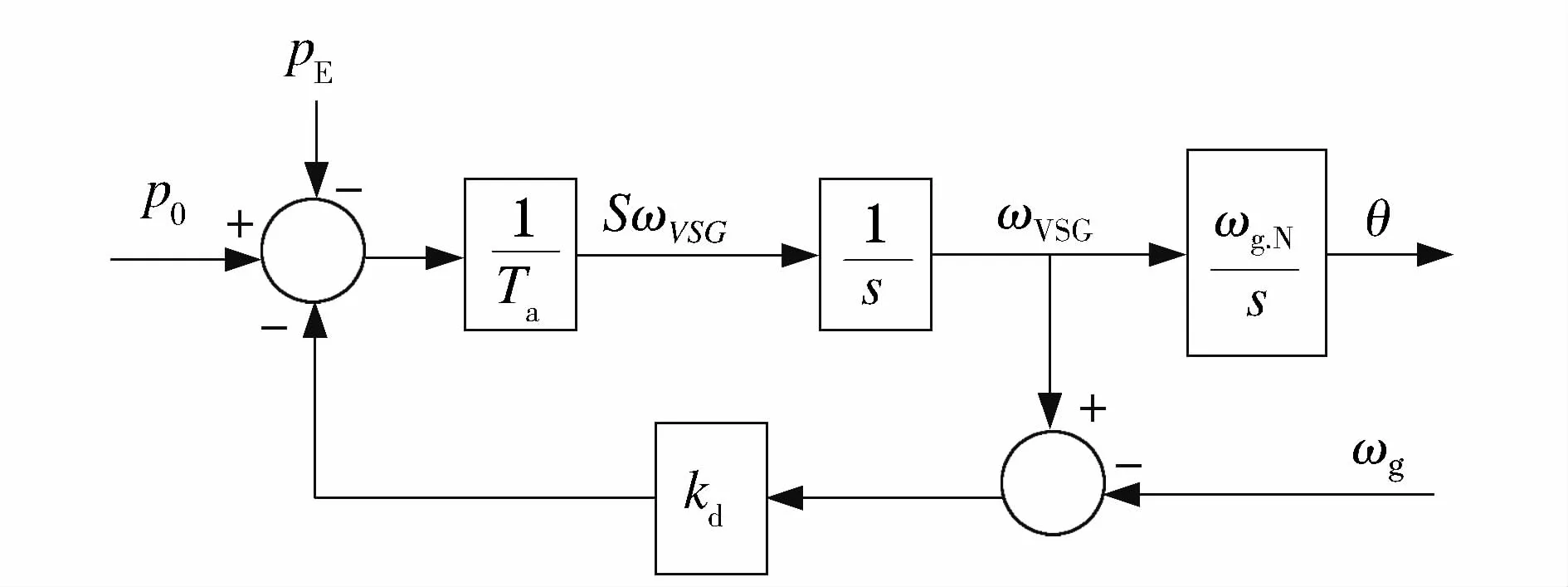
图5 虚拟同步发电机的虚拟惯性控制框图Fig.5 Virtual inertia control block diagram of VSG

图5中，Ta（＝2 H）为表征虚拟惯量的时间常数；kd为阻尼系数（与前文D含义一致），其倒数（kd）-1与下垂系数 Dp等价［16］；ωVSG为虚拟发电机侧角频率；ωg为电网角频率；ωg.N为额定角频率；P0为逆变器有功功率给定值；PE为逆变器有功功率输出值。

仿真过程中，VSG中关键参数的整定至关重要。对于表征虚拟惯量的时间常数Ta，类比传统同步发电机的定义，可按式（14）进行整定计算：

式中Sn为搭建的虚拟发电机的额定容量；J为虚拟转动惯量。阻尼系数D的整定可利用其与有功功率下垂系数Dp的关系来确定，利用电网中对频率质量的要求“允许频率偏移为 ±0.2 Hz～±0.5 Hz”，电网频率变化±1.0%时，有功功率变化±100%，再结合具体仿真中有功功率设定基准值确定Dp；同理在无功-电压下垂控制中，利用“允许电压偏移为±5%”的电压幅值质量要求，即电网电压幅值变化±5%，对应无功变化100%，结合无功功率基准设定值确定无功功率下垂系数Ku。

本文利用Matlab／Simulink仿真平台对虚拟同步机运行控制进行仿真。主电路采用图6所示的拓扑结构，直流电源Udc＝800 V，电网线电压为380 V，电感 Ls＝0.6 mH，滤波电容C＝1 500μF。

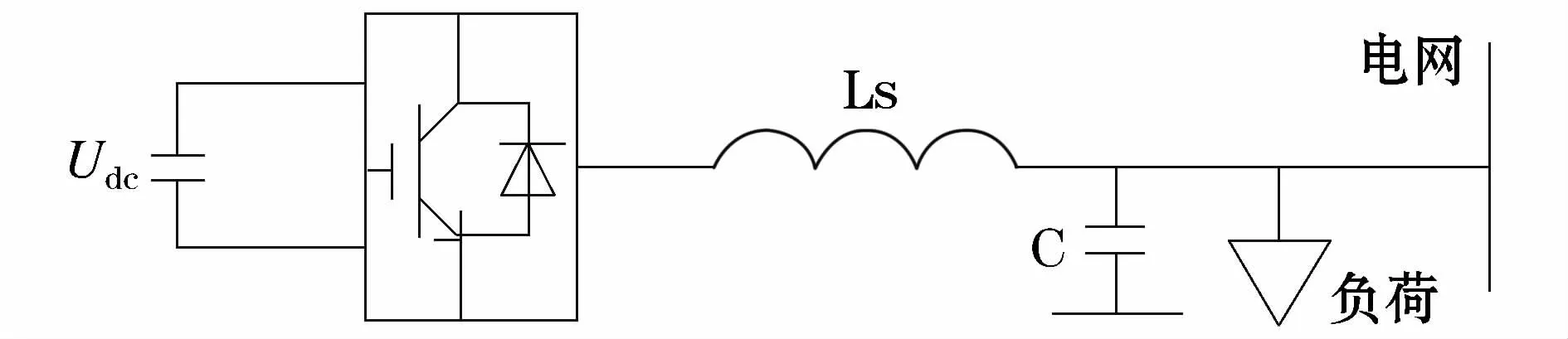
图6 单机无穷大系统拓扑图Fig.6 Topology of single-machine infinite bus system

图7为VSG在单机无穷大下动态仿真图。在初始时刻，逆变电源独立向10 kW的纯电阻性负载供电，电网公共母线电压设置为380 V，系统频率设置为50 Hz。由于所搭建的虚拟发电机容量并不大，将其惯性时间常数设定为1.0 s；PI参数中，电压环控制参数Kup＝10，电流环控制参数Kui＝100，载波频率取6 000 Hz。3.5 s时，将负载的有功功率提高至15 kW，负载的无功功率提高至2 kvar；6.5 s时，负载有功功率重新降到10 kW，无功功率重新下降到0。

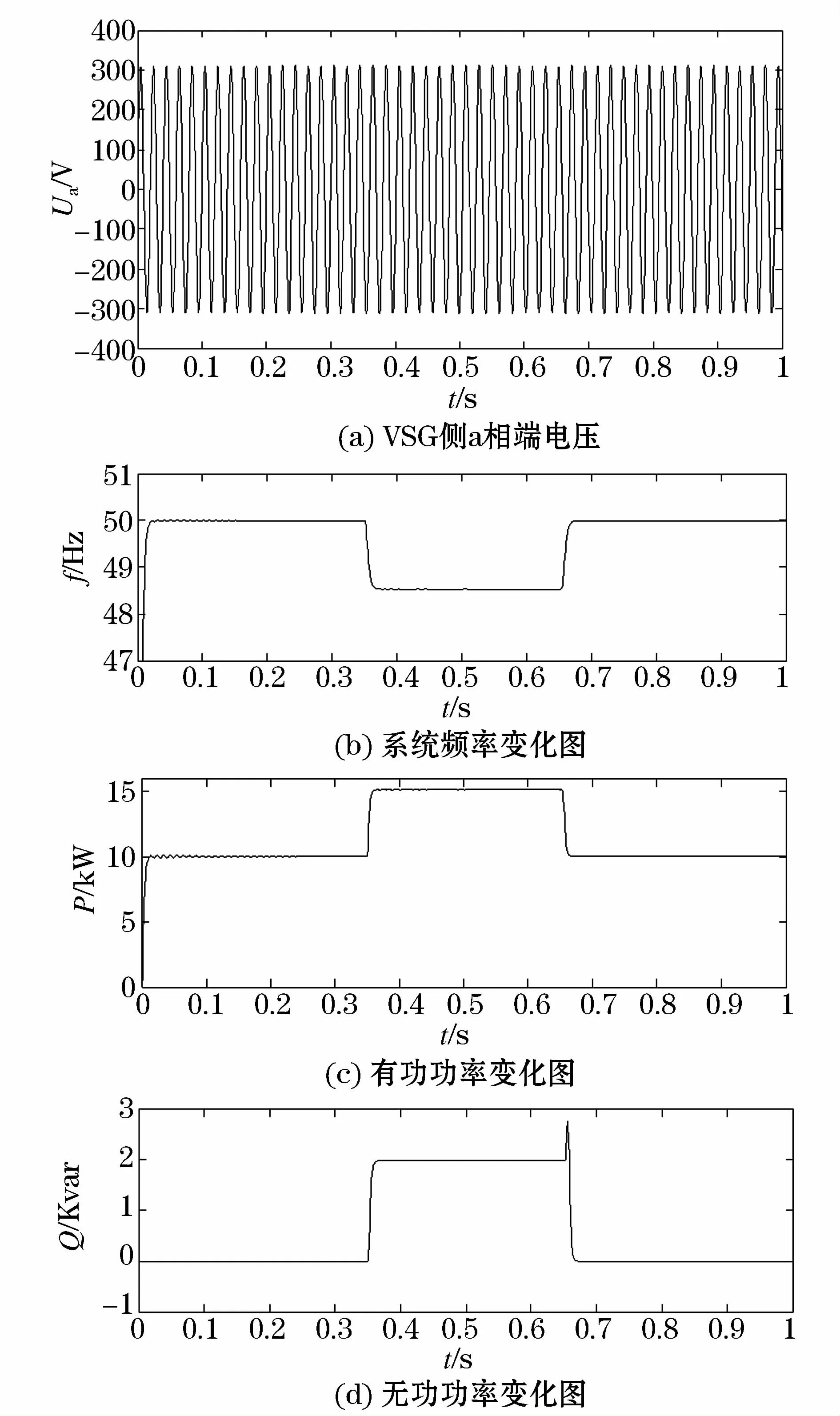
图7 VSG单机无穷大系统下动态仿真图Fig.7 Dynamic simulation diagram under VSG single-machine infinite bus system

从仿真图中可以看出，VSG输出的有功功率和无功功率能够快速跟随负载的变化。3.5 s时，负载有功功率增加，系统的频率发生下降，由有功-频率下垂控制特性决定；同理，因为无功-电压下垂控制特性，无功功率变化时，电压也随着变化。6.5 s时，敷在恢复初始状态，频率和电压也会随着恢复到初始状态。

仿真图中，动态响应波形变化较“陡”，虽然可以快速跟踪功率变化，但并不利于系统稳定运行。从外特性上看，虚拟同步发电机可以视为带有虚拟惯性的下垂控制器。所以对于虚拟惯性的控制十分重要。由于动态响应波形变化较“陡”，说明仿真过程中对虚拟惯性控制不够好，控制参数的设定并不理想，要结合虚拟发电机实际运行情况对参数进行改进，使波形变化更加“平缓”一些，进一步完善虚拟发电机的运行特性，使其更有利于电力系统的稳定运行。

只改变下垂系数，在其他仿真条件不变的情况下得到图8（Dp分别取2e-4和3e-4）。由图8可以看出，下垂系数影响频率的变化幅值：下垂系数越大，系统的频率变化幅值也越大。实际运行中，可以通过改变下垂系数来控制系统的频率变化幅值，给电网提供相应的频率支撑，体现了虚拟发电机控制的灵活性。

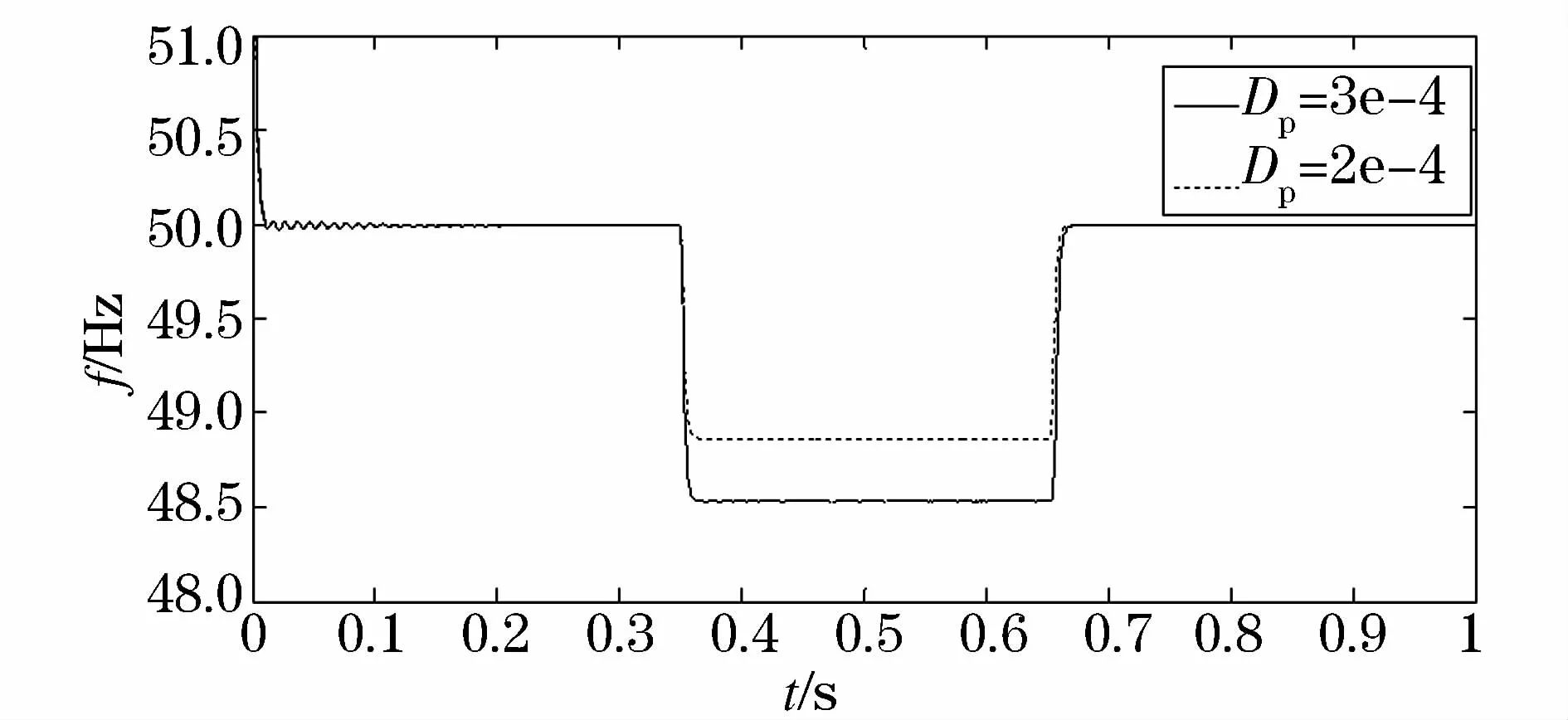
图8 下垂系数对频率的影响Fig.8 Effect of droop coefficients on frequency

只改变VSG的惯性时间常数，在其他仿真条件不变情况下得到图9。由图9可以看出，惯性时间常数影响频率的变化速度，图9（b）中Ta＝2 s的频率变化曲线相对于Ta＝1 s和 Ta＝0.5 s时更“平缓”，响应速度更慢，反应更“迟钝”；图9（c）中 Ta＝2 s时的频率变化曲线最“平缓”，恢复速度最慢；而Ta＝1 s时的频率恢复速度要比Ta＝0.5 s时更快，说明惯性时间常数的选择并不是简单的越大越好或者越小越好，不仅要考虑功率跟踪和频率响应的速度，还要考虑虚拟同步机的容量和实际输出的功率大小等因素。选择一个合适的惯性时间常数对于控制VSG的运行有重要的意义。

图9 惯性时间常数对频率的影响Fig.9 Influence of inertia time constant on frequency

5 结束语

基于逆变器下垂控制的虚拟发电机能够模拟传统同步发电机的外特性，并且在单机系统下能够快速跟踪负载功率变化，维持系统频率在允许范围之内。

虚拟发电机的控制参数设置具有灵活性，实际运行时要根据具体情况设定，选择合适的控制参数，可以给电网提供频率支撑，为VSG技术在电网中的应用提供了理论支持。