基于CPA和FSCC的自适应扰动观察法在MPPT中的应用*

李永刚，于德水，周一辰，庞春江，霍明霞

（1.华北电力大学，河北 保定071003；2.河南省济源供电公司，河南 济源459000）

0 引 言

近年来，发电需求的迅速增加和常规能源（如煤和石油）的匮乏使得可再生能源的发电迅猛发展。光伏发电因其普遍适用、免费、环保的优点以及较少的操作和维护成本低逐渐成为传统能源的理想替代［1］。为使光伏系统离线或并网发电运行时更加高效，需要一种适用性强且高效的最大功率点跟踪技术（MPPT）来捕捉时变条件下的最大功率点［2-3］。

目前文献中MPPT有传统的扰动观察法，电导增量法，恒定电压比法，模糊逻辑控制器（FLC），自寻优占空比法。这些控制方法的区别在于实际最大功率点振荡，收敛速度，复杂性，稳定性以及电气设备的成本［4］。电压扰动观察法可能是目前的MPPT算法中最常用的，因其算法较简便且仅需测量光伏电池的输出电压和电流。但在最大功率点稳态运行时会发生功率振荡造成损耗。电流扰动（CPA）相比电压扰动在MPPT附近时，仅需较小的步长追踪光伏最大功率点。所以有效减小最大功率点附近的振荡现象。局部短路电流（FSCC）能在跟踪初期将光伏阵列工作点电流调整到光伏最大功率点附近，以保证跟踪的快速性。局部短路电流法能实现光伏系统的快速启动，且成本低、容易实施。但不能保证始终工作在最大功率点。

为解决传统P＆O较大的功率损耗，并结合恒流启动提高MPPT跟踪速度，本文搭建了MPPT控制系统仿真模型，将电流扰动（CPA）和局部短路电流（FSCC）结合，利用恒流启动，引入温度调整系数，计算最大功率点电压补偿值，来提高启动速度和外界环境的敏感性［5］；利用自适应扰动法调整扰动步长，改善功率振荡。

1 光伏系统模型

1.1 光伏电池模型

PV电池的电特性与二极管PN结相似。它通过使用光子产生电子。它具有吸收太阳辐射，并将光子移动到电子直到它收敛的能力。

当负载接至PV电池时，电荷以直流电流形式流过它，直到光照结束。

太阳能电池的电压-电流关系为：

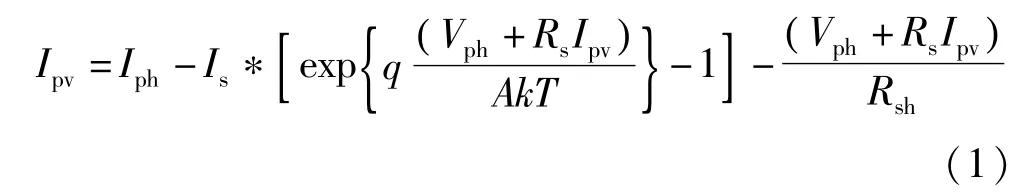
Vph和Iph分别表示光伏阵列输出电压和输出电流，Is为PN节间的反向饱和电流；q是电子电荷量；A是PN节的理想因数；K是玻尔兹曼常量；T是环境温度；Rs和 Rsh分别是电池的串联电阻和并联电阻［6］。

1.2 DC-DC升压电路

DC-DC升压电路用来优化光伏模块输出的功率，图1展示了升压斩波电路的结构。

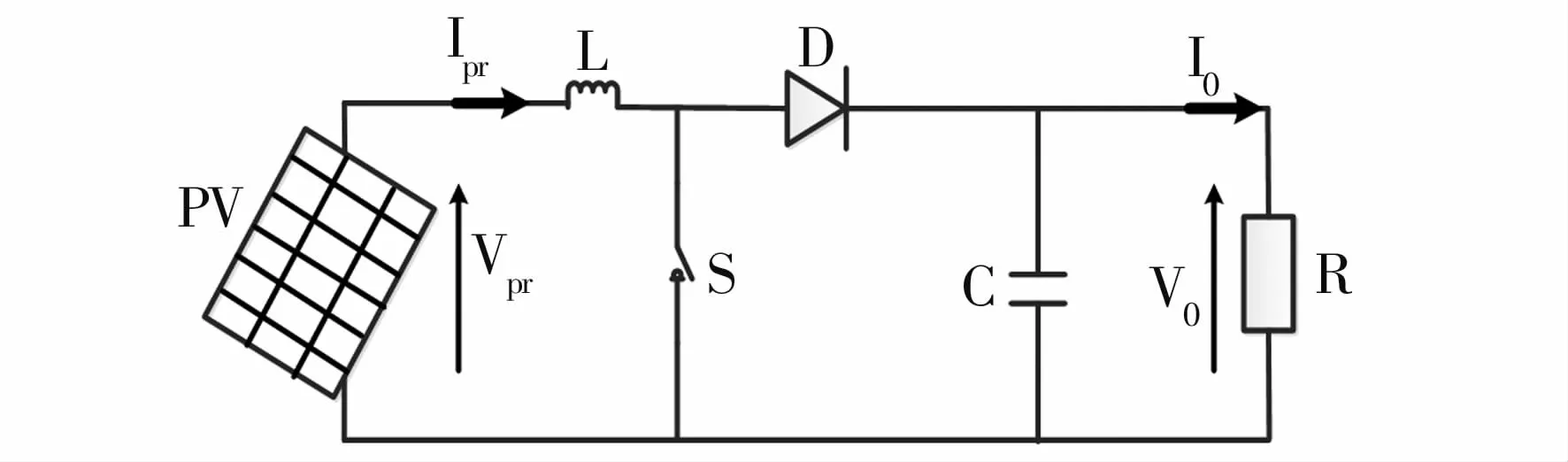
图1 DC-DC升压电路Fig.1 DC-DC boost circuit

其中s是主开关；L为滤波电感；C为滤波电容；R为电阻负荷。建立动态模型如下：

Ipv，Vpv，Vo和D分别为升压电路的输入电流，输入电压，输出电压以及输出占空比。假设Boost电路处于电流连续模式，当开关S闭合时，电感L中的电流会线性增大，此时二极管D关断。当开关S断开时，电感中储存的电能将会通过与二极管连接的RC电路消耗。

Boost电路处于稳定状态时，电感L平均电压在扰动周期T中为零；故Boost电路输出电压：

Boost电路工作在连续电流模式时L＞Lmin，

滤波电容最小值为：

式中f是开关频率；R是电阻负载。由上可知输出电压和输入电压的关系取决于占空比，假设传递效率η＝100%，则换流器的输入功率等于输出功率。从而电阻负载：

2 最大功率跟踪策略

2.1 改进型定步长扰动法

传统改进型定步长扰动法采用恒压启动，光伏阵列启动时首先对光伏阵列的开路电压进行采样，未考虑温度变化对输出特性的影响。根据图2知光伏阵列在特定温度和光照下存在一个最大功率点，且存在Um＝0.78·Uoc。将Um作为电压设定值，控制光伏阵列的输出电压由开路电压下降至电压设定值（随着输出电压下降，输出功率向MPP方向移动），最后改换为定步长P＆O。该算法的控制流程框图如图3所示。

图2 不同光照强度下的输出特性曲线图Fig.2 Output characteristics curveswith different intensities

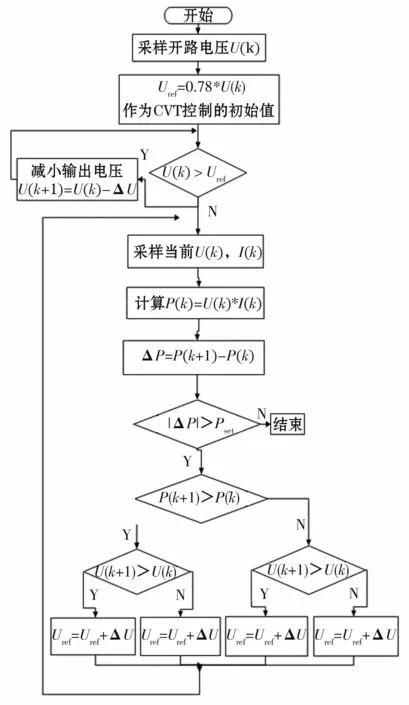
图3 传统改进型定步长扰动观察法Fig.3 Traditionalmodified step-perturbation observation method

2.2 基于CPA和FSCC的自适应扰动观察法

为使光伏系统启动时能快速跟踪到MPP，本文在系统启动采用局部短路电流法（FSCC）。即采样电流I（k）不满足：Im≦ I（k）≦ IM条件时。其中 IM和Im分别定义如下［6］：

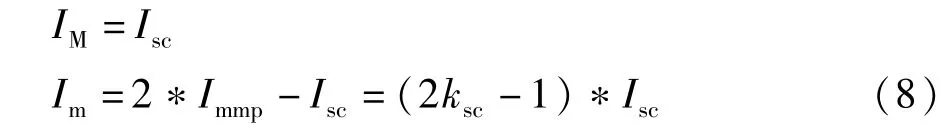
局部短路电流法能在跟踪初期将光伏阵列工作点电流调整到最大功率点附近，以保证跟踪的快速性。在不同的环境条件下最大功率点电流与短路电流之间的近似线性关系：

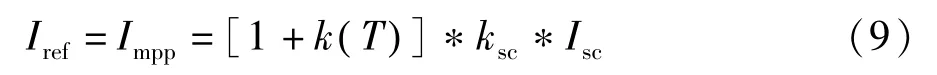
比例系数ksc一般在0.78～0.9之间。但在对控制方法的简化过程中，忽视了温度变化会使PV输出功率与最大功率点存在偏差，出现一定的功率损失。为解决此问题，本文在局部短路电流法启动过程中，系统将当前采样温度T（k）与前一时刻采样点T（k-1）比较。若偏差大于误差范围e（T），引入温度校正系数K（T）来校正电流参考值，其中温度校正系数约为 K（T）＝-0.405%／K；当温度差很小时，K（T）＝0。从而对控制信号进行调整［7］。

随着光伏输出电流增大，当采样电流I（k）满足：Im≦I（k）≦IM条件时，即工作点在最大功率点附近运行时，采用电流扰动法（CPA）。电流扰动相比电压扰动在最大功率点附近时，仅需较小的步长追踪光伏最大功率点。其中参考电流值如下。

若由于外界环境使光照强度迅速改变，

基于CPA和FSCC的自适应扰动观察法能减少在稳定状态下的最大功率点振荡的次数，并且将两种算法（CPA和FSCC）的优点结合起来追踪快速变化环境时的最大功率点，如图4所示。

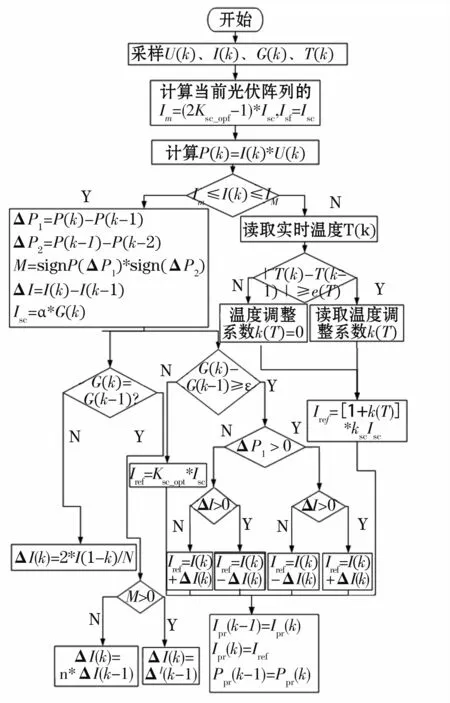
图4 基于CPA和FSCC的自适应扰动观察法流程图Fig.4 Flow chart of adaptive perturbation observation based on CPA and FSCC

短路电流值可根据光照强度变化而改变：

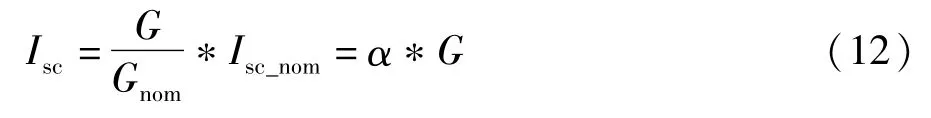
因此，一旦光照强度确定了，根据式（12）短路电流值就确定了。对于ΔI（k）可由变步长自适应扰动观察法［8］的 MPPT策略确定。减小 ΔI（k）可降低振荡引起的稳态损耗，因此电流扰动幅值是很重要的参数，需要进行优化。可变电流扰动步长ΔI（k）可根据光照强度变化值确定。当光照强度不变时，ΔI（k）可定义如下：

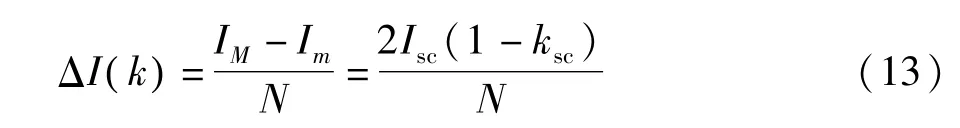
其中N为所需的最大迭代次数。当光照强度变化时，根据变量 M＝0时，ΔI（k）＝ΔI（k-1）。

M＞0时：

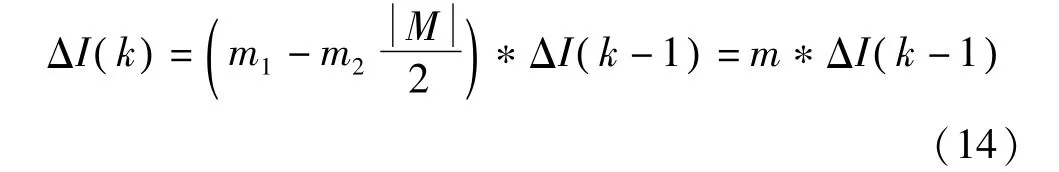
其中m1为扰动步长的减小因子且m2＝1-m1，变量M引起在最大功率点附近的工作点的振荡，定义如下：M＝signΔPpv1*signΔPpv2。

其中，Ppv1＝Ppv（k-1）-Ppv（k-1），Ppv2＝-Ppv（k-2）+Ppv（k-1）。为使工作点在MPP附近移动，扰动步长会因m1减小而减小，如表1所示。

表1 扰动步长动态值Tab.1 Perturbation step dynamic value

3 仿真实验与结果对比

3.1 仿真模型和仿真参数

MPPT控制系统仿真模型采样时间为10μs，采用了定步长Discrete算法。该光伏阵列开路电压21.9 V，短路电流 4.96 A，最大功率点电流 4.58 A，最大功率点电压17.5 V，温度为25℃，光照强度为1 000 W／m2时最大功率输出为80 W。光照强度为600 W／m2最大功率输出 48 W［9］。

为验证本文所提算法在提高光伏系统稳态输出的稳定性，温度为25℃，将光照强度在0.5 s时由1 000 W／m2突变到600 W／m2，观察 PV系统在两种MPPT算法控制下的输出功率。 图6（a）为光照强度，图6（b）为是本文提出的基于CPA和FSCC的自适应扰动观察法，图6（c）为改进型扰动观察法。表2表示光照突变时光伏阵列输出功率最大波动量和恢复稳定输出所需时间［10］。

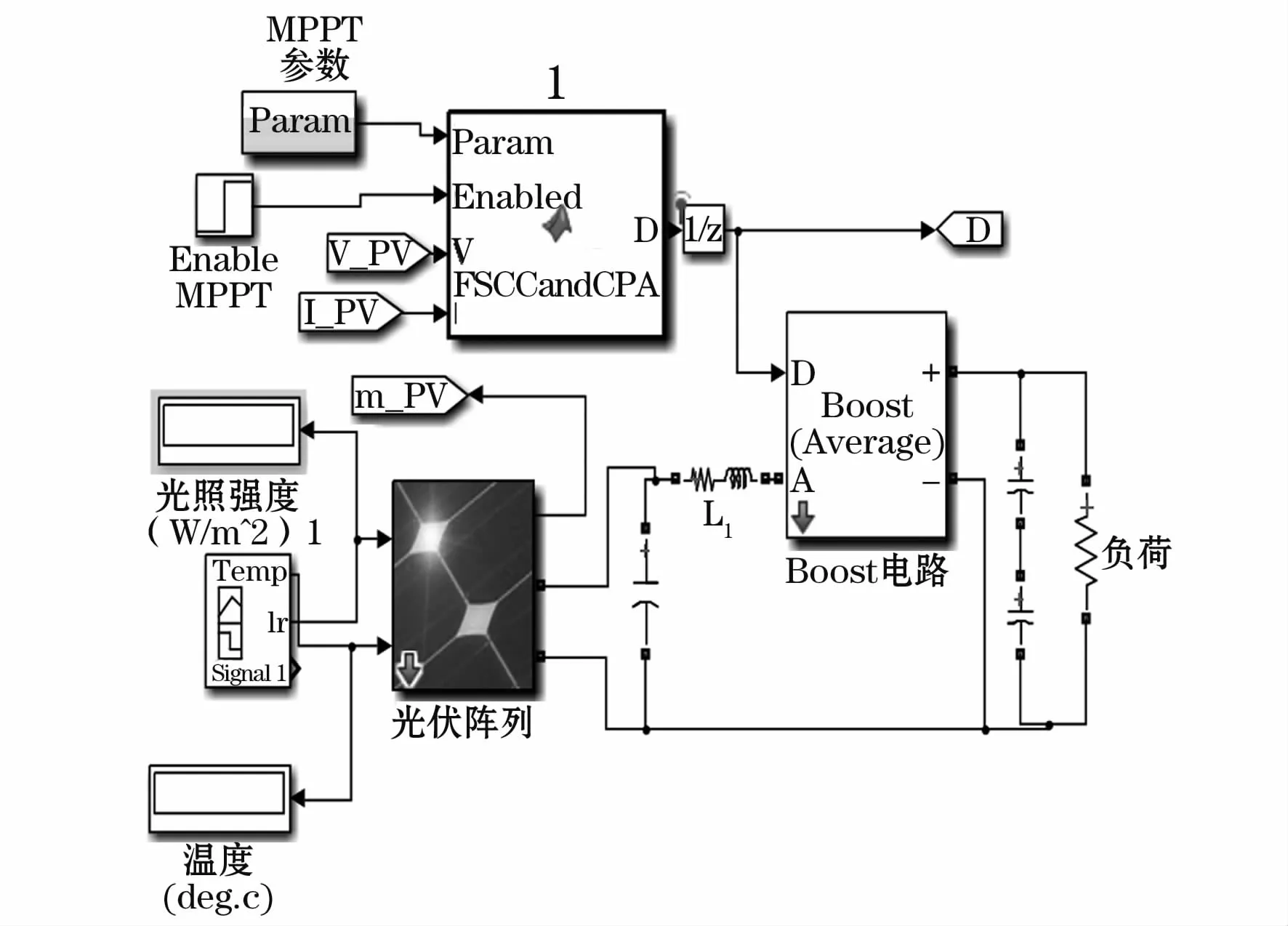
图5 MPPT控制系统仿真模型Fig.5 MPPT control system simulation model

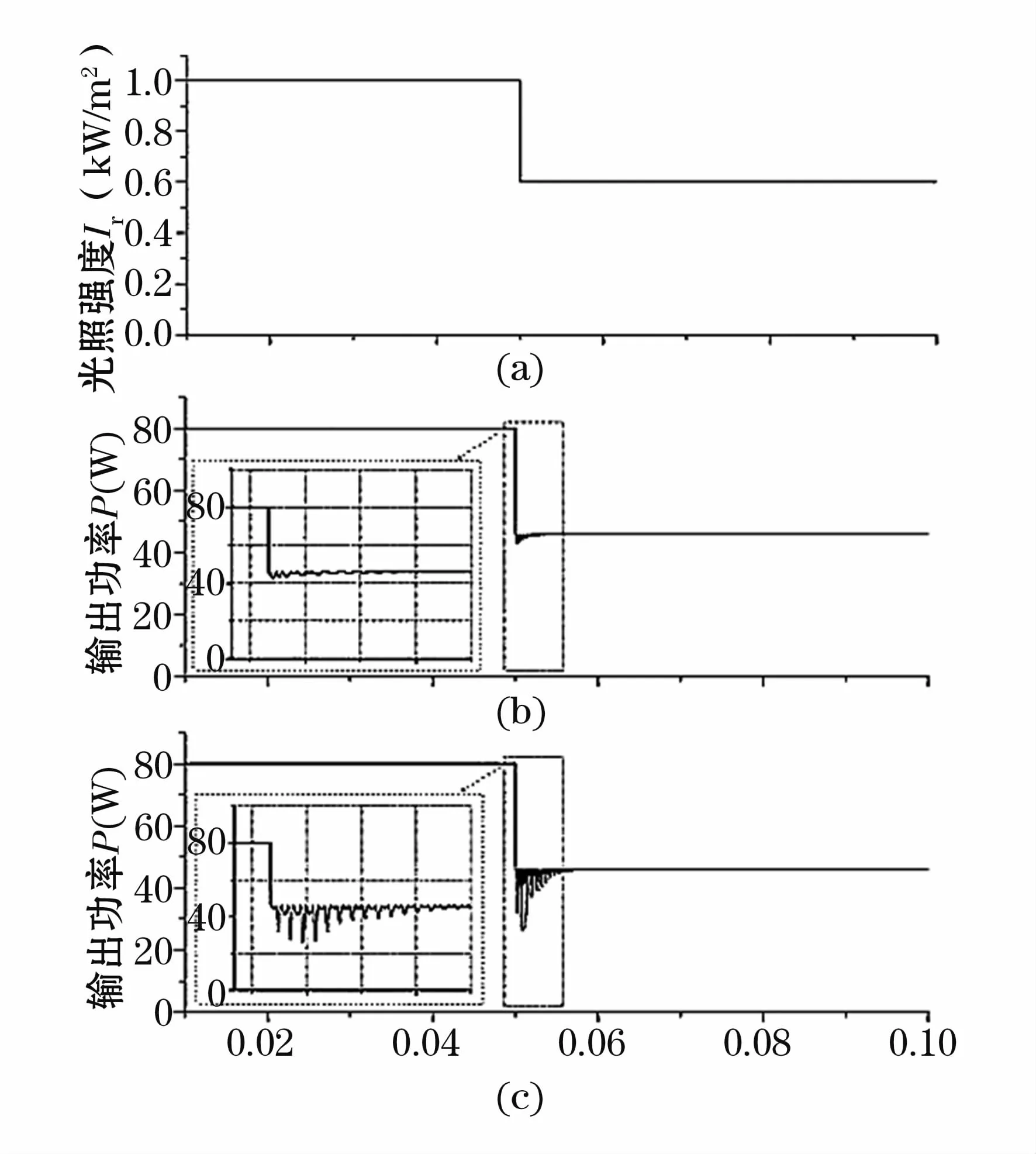
图6 PV系统在两种MPPT算法控制下的输出功率Fig.6 Output power of PV system under the control of two MPPT algorithms

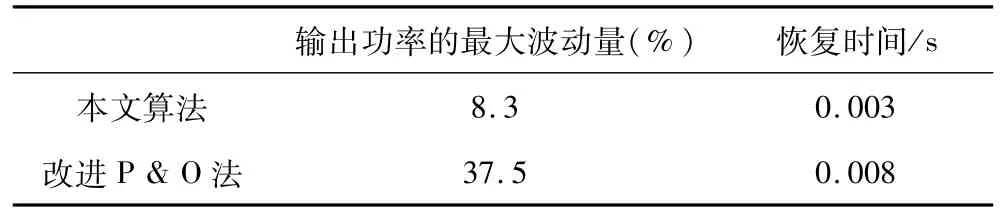
表2 输出功率稳定时的最大波动量Tab.2 Themaximum fluctuation when the output power is stable

从实验结果来看，当光照强度在0.05 s时由1 000 W／m2突变到600W／m2时，本文算法对光照强度变化的响应时间仅为0.003 s，快于传统改进法，能较快的跟踪到光照强度瞬时变化。由表3知改进算法稳态输出功率为480W时最大波动量达37.5%，而本文所提算法下仅为8.3%。本文所提算法最大率输出时波动量远低于传统改进算法，能很好解决功率稳态输出时的振荡问题。

表3 系统参数值Tab.3 System parameter value

为验证本文算法引入温度调整系数对改善系统启动时间和对外界温度变化的敏感性，将温度从24.25℃递增至25.5℃，光照强度恒为1 000W／m2，观察PV系统在两种MPPT算法控制下的输出功率。

从实验结果来看，如图7。当外界温度从24.25℃递增至25℃，图7（a）中启动时间约为0.06 s，而图7（b）仅为 0.04 s。图 7（a）输出功率低于正常最大输出功率80 W，在0.05 s到0.15 s期间，出现坡底后恢复正常。而图7（b）中输出功率比较稳定。可知引入温度调整系数可改善系统启动时间和对外界温度变化的敏感性，当外界温度不断变化时，本文算法与传统改进型扰动法相比，输出稳定性高，波动较小，具有很好的动态性能。

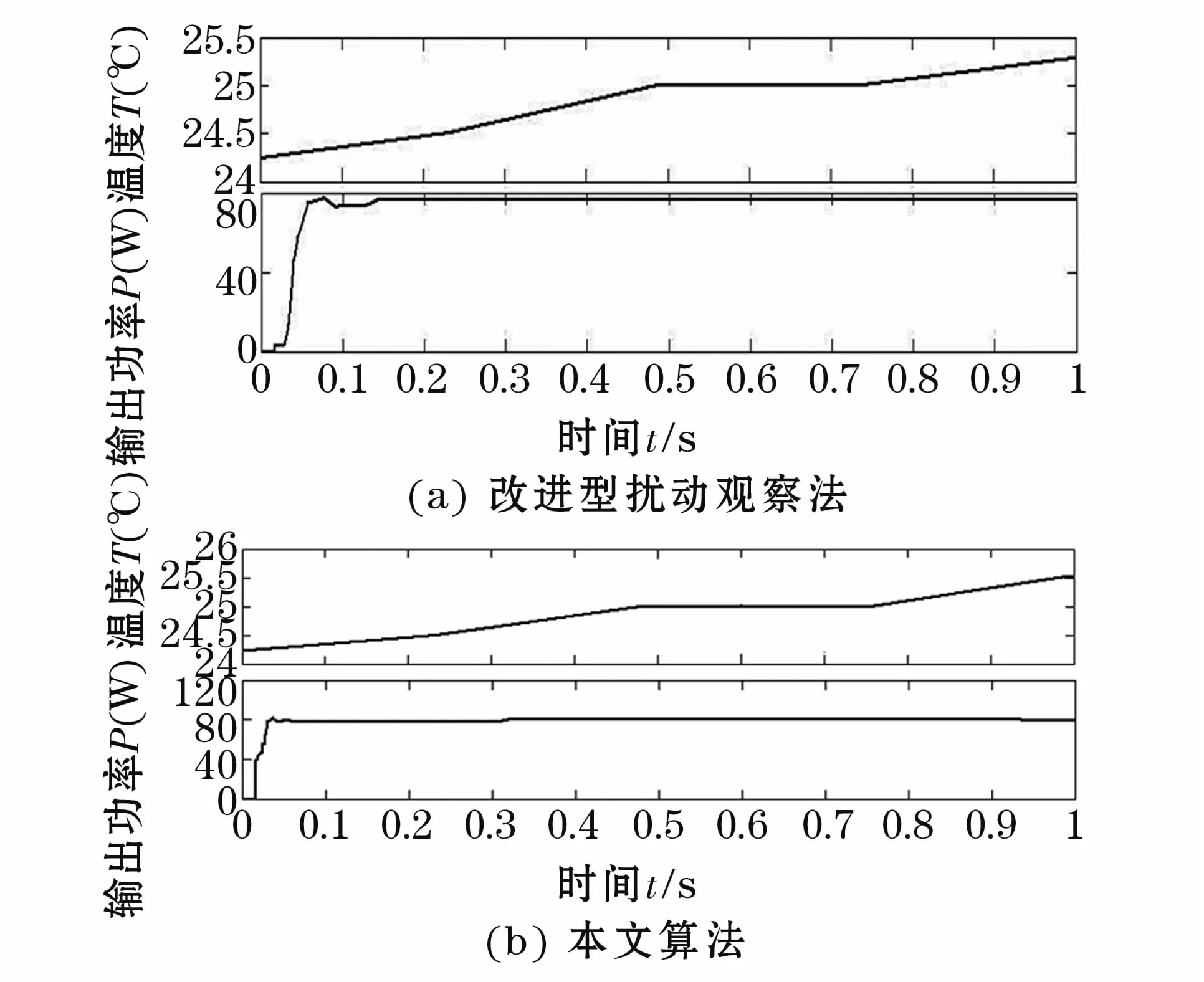
图7 光照强度为1 000W／m2，温度变化时PV系统的输出功率和输出电压Fig.7 Illumination of 1 000 W／m2，the temperature changes PV system output power and output voltage

4 结束语

相比传统改进型扰动观察法，所提出的方法可以通过FSCC进行快速启动，同时引入温度校正系数来算出最大功率点电压校正值，应对外界温度迅速变化。工作点能快速接近最大功率点，输出稳定性高，波动较小，具有很好的动态性能。启动完成后，结合CPA和FSCC的优点，利用自适应扰动法调整扰动步长，可以减轻系统在稳态时的功率振荡。仿真结果表明，该算法能有效削弱功率振荡现象。同时可快速跟踪外界温度和光照强度的变化。