基于重建策略的云工作流调度算法优化

林海涛,姜栋瀚

(海军工程大学 电子工程学院，武汉 430033)

基于重建策略的云工作流调度算法优化

林海涛,姜栋瀚

(海军工程大学 电子工程学院，武汉 430033)

为了进一步提高算法性能，提出一种改进的蛙跳算法，并与调度方案相结合，以期为云工作流资源分配提供最优调度。通过在蛙跳算法的局部搜索中加入重建策略，提高了数据随机性，有效避免了局部最优。研究了调度方案生成算法，与改进算法相结合得到接近最优的调度。利用Java模拟器进行仿真试验，并与粒子群优化算法和传统蛙跳算法作比较。实验证明，提出的方法可以在满足最长截止时间约束的情况下，使总执行成本最小化。

蛙跳算法；资源调度；云工作流；重建策略

0 引 言

基础设施即服务(IaaS)是云计算最基本的应用形式[1]。当用户提出应用请求后，IaaS通过管理中间件中的任务管理机制为任务分配虚拟化资源，其资源调度机制是影响云计算效能的关键。云计算中的按需配置和资源可用性使其成为执行工作流应用程序的理想选择。然而，工作流调度是一个非确定性多项式(non-deterministic polynomial，NP)问题，云计算环境的异质性和动态性又使问题进一步复杂化。资源调度高效算法是提升云工作流系统效能亟待解决的问题，也是云计算领域内的研究热点。

工作流是指将一组任务按照业务需求进行合理传递的工作流程。工作流中任务数量大小不等，但所有任务需要分配至不同的虚拟资源，并在合理的时间内完成。而云计算环境下，服务器被虚拟化成可在同一处理器上运行的多个虚拟机(virtual machine,VM)，不同的虚拟机具有不同的CPU、内存和带宽等资源。资源调度算法就是确定任务和虚拟资源之间的映射，以便满足一个或多个优化目标。

国内外已经提出了很多云计算环境下的资源调度方案，概括来说主要有2种：①基于最优化理论对云计算资源调度问题建模，以实现整个系统的性能最佳。例如文献[2]中通过动态箱包装，最小化在包装中使用的最大箱数，实现了云计算整体消耗的最小化；文献[3]中提出的自适应调度算法(adaptive scheduling algorithm，ASA)首先将任务从逻辑上分成若干类别，再根据不同资源的特点进行合理分配。上述算法在调度的过程中实现了整体效能的最优，被广泛应用于小规模的虚拟机部署方案。但是，在分布式系统上进行资源调度是NP问题，该问题无法在多项式时间内获得最优解。尤其在规模较大时，上述算法难以在有效时间内得到最优解。因此，另一种基于启发式的次优算法被提出。②基于启发式的次优算法，是指在可接受的范围内得到可行解来处理实际问题。例如文献[4]中提出了模拟退火算法(simulated annealing algorithm，SAA)，模拟物理学中的冷却过程通过内外循环使其达到热平衡状态。即用更优解替换原有解，经过多次迭代找到较好的分配方案；文献[5]中介绍了遗传算法(genetic algorithm，GA)，通过初始化、交叉和变异算子，经过多次迭代最终找到较优解；文献[6]提出的粒子群优化(particle swarm optimization，PSO)算法通过在空间中找寻适应度最优的粒子，找到最佳位置，从而更好地进行资源调度；在蛙跳算法(shuffled frog leaping algorithm，SFLA)中，通过子种群群内通信和群间通信，最差解不断定向跳跃至最好解的位置，它作为一个有效的算法被应用在各种资源调度中，如聚类、演化查询、排序优化、推荐系统等[7]。但是上述算法大多不具有约束能力，尤其在规模较大时，容易陷入局部最优，难以得到全局最优解。为了进一步提高算法性能，本文对SFLA进行了改进，以期为云计算资源调度建模提供思路。

1 问题描述

1.1 问题说明

执行一个大型工作流，首先将其分成多个小任务，并将其映射在虚拟资源上。云工作流的资源调度一般分为3个步骤：①提供可以用来分配给任务的可用资源；②将任务映射到满足需求的资源上；③按照之前的映射方案将任务分配到相应资源上运行。本文所提出的算法结合了资源提供和调度的问题，并将它们作为一个问题，使用改进的蛙跳算法加以解决。目的就是将工作流中的每个任务映射到更好的服务资源，使总执行成本最小化，并将完成时间保持在最后期限内。

工作流可以描述为有向无环图(T,E,D)，其中，点集合T表示业务应用的任务集合；E表示任务之间的依赖关系，即沿边缘方向的权重值(边缘权重)；最后期限D表示工作流应该完成的最长执行时间。虚拟机的处理能力根据每秒浮点运算次数来确定，并且可从云资源提供者处获得。基于虚拟机的处理能力，可以计算给定虚拟机上任务的执行时间。如果T1在任务图中位于T2之前，即在T2任务开始执行之前要完成T1任务，则从节点1到节点2存在有向边。没有传入边的节点表示进入任务，没有传出边的节点表示退出任务。一种工作流示例如图1所示。

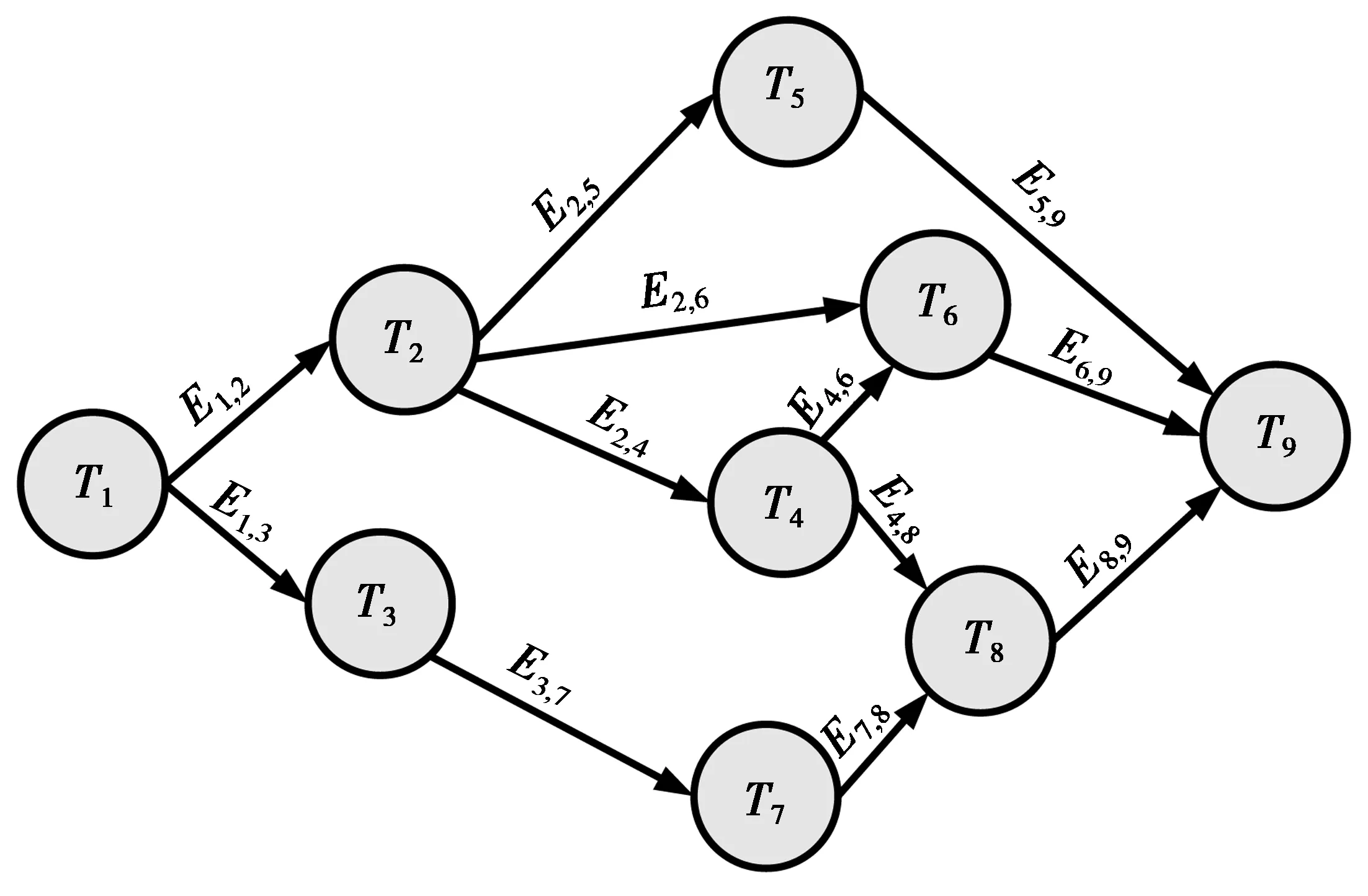
图1 一种工作流示例Fig.1 A workflow example

图2描绘了与图1任务图相对应的调度示例。

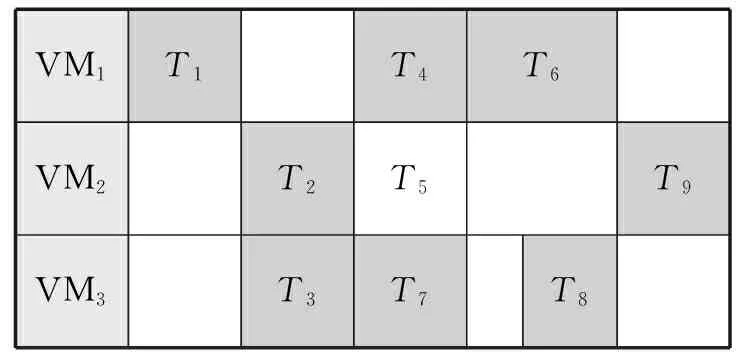
VM1T1T4T6VM2T2T5T9VM3T3T7T8

图2调度示例
Fig.2 Example of scheduling

工作流中常见的优化标准是任务完成时间的最小化、成本最小化、资源利用最大化、满足目标约束等。除此之外，还需要调度算法来协调工作流中的任务依赖性，即在某些情况下，只有当工作流中的前一个任务已完成执行时，才能执行下一个任务。另外，云计算环境对于工作流更为有益，因为它使用户能直接请求业务所需的资源，并且由用户控制的调度器来调度任务[8]。这使得用户能够仅在需要时分配资源，并且一旦分配，该资源可以随后用于执行多种任务。因此，高效的资源调度是在云中实现高性能的主要挑战[9]。假设各种类型的VM由IaaS提供商提供，用户可以根据需求按需租用它们。本文提出的调度算法定义任务和资源之间的映射，并列出了应租借的VM的数量以及应租用的时间长度。目的是使总执行成本最小化并将完成时间保持在期限内。

1.2 基于重建策略改进蛙跳算法

2003年，Eusuff和Lansey提出SFLA[10]，旨在模仿一群青蛙的行为，寻找随机分布在池塘里的石头上的食物。它汇集了基于遗传进化的模因演算法(memetic algorithm，MA)以及基于社会行为的粒子群优化(particle swarm optimization，PSO)算法，其已被用于解决诸如资源调度、车间作业生产调度等许多复杂的优化问题。

在传统的蛙跳算法中，初始种群由一组在池塘中寻找食物的青蛙组成。搜索食物包括2个交替的过程：①初始种群被分为若干个子种群，在子种群内青蛙进行群内通信；②子种群发展到一定阶段，它们之间进行群间通信。这个过程中，只有最差解被定向跳跃至最好解的位置。然而，由于种群是随机生成的，即使适应度最好的青蛙也可能不具有真正的全局性，从而易导致局部最优。越是食物密集的地方越容易陷入局部最优，并且搜索食物的青蛙的跳跃动作取决于个体的惯性运动，因此，在最好解的周围可能存在具有更多食物的位置。这可以通过更新最佳蛙的惯性矩来实现。

因此，我们设计了一种重建策略，重建策略流程如图3所示。在得到的最好解周围找随机位置，进行适应度比较。这种方法有助于最好解跳跃到其附近有更多食物的新位置。在每个模因中，对于每次迭代确定最佳和最差解。对于模因中的替代迭代，最好的青蛙试图重新建立自我地位以增强他们的位置，而最坏的青蛙努力通过所有迭代中的信息交互来改善他们的位置。该策略可以用于解决任何种类的离散或连续优化问题。对于任务调度，通过在最佳解决方案处搜索更好的位置来执行重建。如果适应度改进，则保留适配的解;否则，最好的青蛙保持在其原始位置。

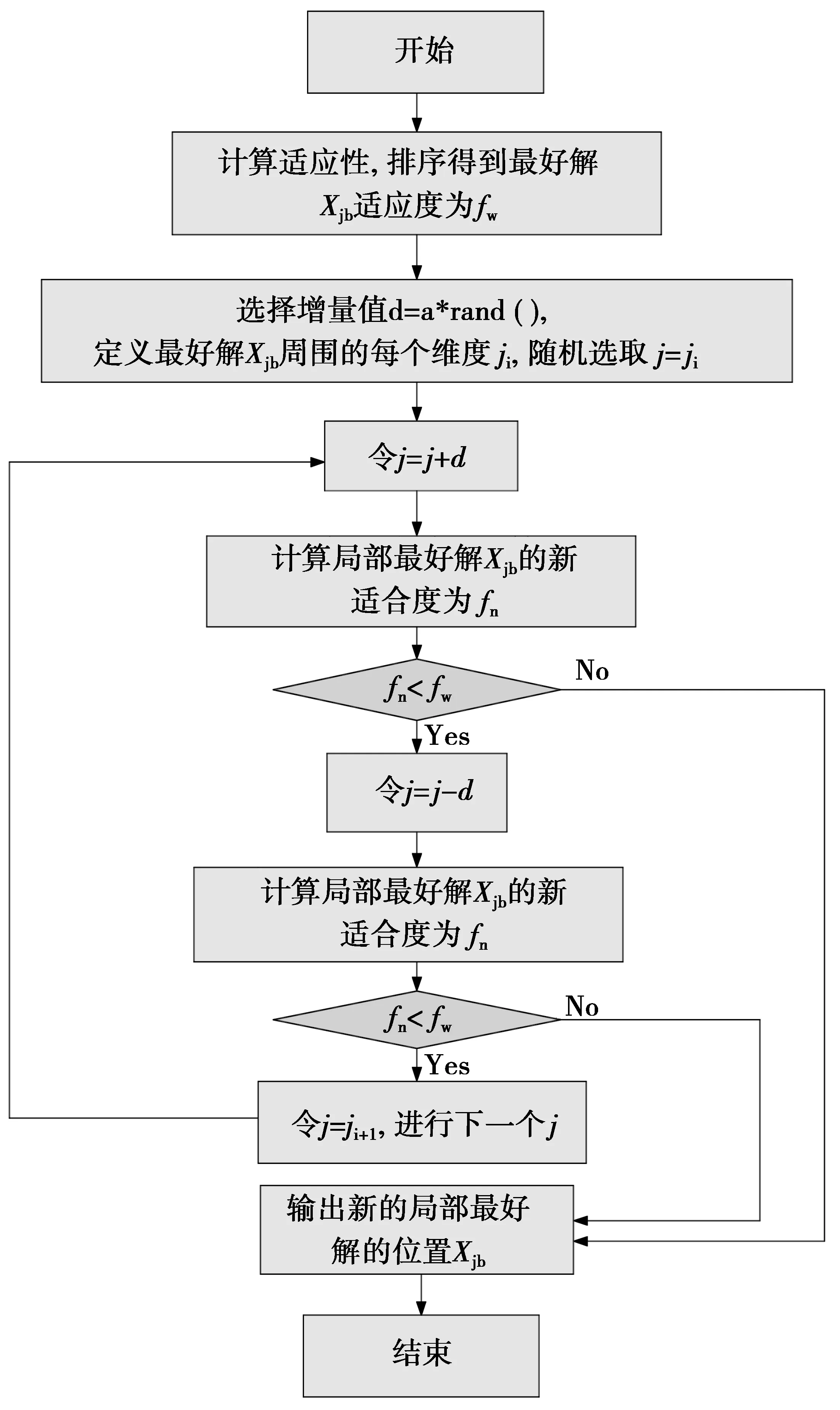
图3 重建策略流程图Fig.3 Reconstruction strategy flow chart

图3中，rand( )函数用来生成0到1之间的随机数；Xqb为全局适应度最好的青蛙，即全局最好解；Xjb为子种群中适应度最好的青蛙，即局部最好解；Xw为子种群中适应度最差的青蛙，即局部最差解；a是适合于该问题的常数值。

改进的蛙跳算法中的演变是沿着2个维度进行的：①通过在种群迭代进化期间恢复最好解的位置；②通过信息交换定期改善最差解的位置。因此，该算法已经被修改为如下所示。步骤1到步骤5保持原算法不变。

步骤1将青蛙的大小设置为d；

步骤2用随机位置初始化青蛙种群P，计算每只青蛙的适应度；

步骤3按照其适应度的降序对种群P进行排序；

步骤4确定全局最好解Xqb的适应度为fqb；

步骤5将P分成m个子种群；

步骤6对于每个子种群

①确定局部最好解Xjb的适应度为fjb，局部最差解Xw的适应度为fw；

②通过替代迭代尝试改善局部最好解的位置(即周期性n=2)；

③新的局部最好解Xn=重建Xjb；

④如果局部最好解Xn的适应度提高，用新青蛙替换原来的青蛙；

⑤使用(1)式相对于局部最好解Xjb，改善局部最差解的位置。如果适应度改善，更新局部最差解的位置。

跳跃步长为

Dd=rand×(Xjb-Xw)

(1)

新位置为

(2)

如果局部最差解的新位置改进，即适应度更高，则其代替最差解；

⑥否则，使用方程(3)相对于全局最好解Xqb，改善局部最差解的位置。如果位置改善，更新局部最差解的位置；

跳跃步长为

Dd=rand×(Xqb-Xw)

(3)

新位置为

(4)

⑦否则，使用新的随机生成的解决方案替换最差解；

步骤7将各进化后的子种群混合，按照其适应度的降序对种群P进行重新排序；

步骤8检查是否满足收敛要求。是，则结束算法；否则，转到步骤3。

在步骤6中，通过子种群内的迭代，确定最好解和最差解。对于子种群中的迭代进化，局部最好解尝试重建以增强他们的位置，而局部最差解努力通过所有迭代中的信息交换改善他们的位置。

2 资源调度方案

当前用于资源调度的解决方案面临成本效率比不高的问题，需要探索更好的解决方案。本文提出了一种基于改进蛙跳算法的方案，所述算法在最小化成本的同时，具有满足最后期限约束的能力。

2.1 问题建模

下面将调度问题建模为改进蛙跳算法问题，假设将第k个工作流中的d个任务调度到r个资源上。工作流被表示为青蛙，每只青蛙携带一个由d个记忆模块构成的模因，对应于任务工作流。第k个蛙F(k)表示为d个记忆值的向量。单元格的数量(即单元的维度)d，由工作流中的任务数量确定。青蛙的坐标范围和数量由资源的数量r决定。此外，可用资源的数量r表示搜索中允许青蛙移动的空间中的食物量。因此，坐标的值在0和其可用的资源数r之间。青蛙的位置代表任务到资源的映射。例如，一个青蛙是10维的，则其位置由10个坐标表示，因为它表示具有10个任务的工作流，坐标值如表1所示。如果有4个资源可用，那么青蛙的每个坐标可以具有在0～4的值。任务与资源的映射关系如表2所示，这里，第7坐标的值1.9表示任务7已经被映射到资源2。符号Mi指青蛙的第i个坐标，并且对应于工作流中的任务ti。

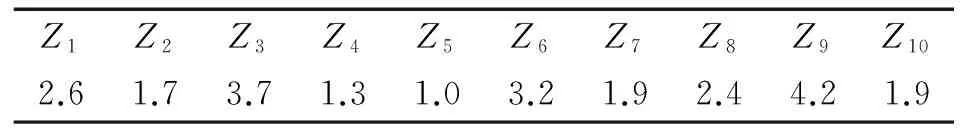
表1 坐标值Tab.1 Coordinate values

表2 任务与资源映射关系表Tab.2 Task and resource mapping relationship table

2.2 调度方案生成算法

本文所提出的算法目标是最小化工作流的总执行成本，并且满足用户要求的截止时间。使用改进的SFLA获得调度和资源供应问题的解决方案包括以青蛙形式生成调度方案，随后使用适应度函数计算蛙的适应度的值。适应度函数是基于优化问题的目标，因此，我们评估每个调度计划的总执行成本，并将其用作适应度函数。

假定最初v为应用程序租用虚拟机的数量，即在工作流中并行执行任务的数量。假设工作流中的任务集由数组T给出。用文献[11]中的方法计算每个资源上的任务ti所花费的时间，可以在初始虚拟机组集合(initial virtual machine，IVM)中计算。时间由n×v矩阵ETM表示，其中，n是工作流中的任务数量，v是IVM中虚拟机的数量。此外，工作流中的任务可以依赖于工作流中用于其输出的其他任务。因此，我们通过n×n矩阵DM表示工作流的依赖性，如果任务ti取决于任务tj(任务tj是子任务)，则DM[i][j]=1，否则为0。将任务的输出传送到其子任务所花费的时间存储在n×n矩阵TTM中。

通过遍历青蛙的每个记忆类型来评估青蛙的适应度，的维度对应于任务ti，并且其值对应于由IVM给出的虚拟机。任务开始的时间取决于它所依赖任务的完成时间和虚拟机可用的时间。算法使用的符号说明如表3所示。

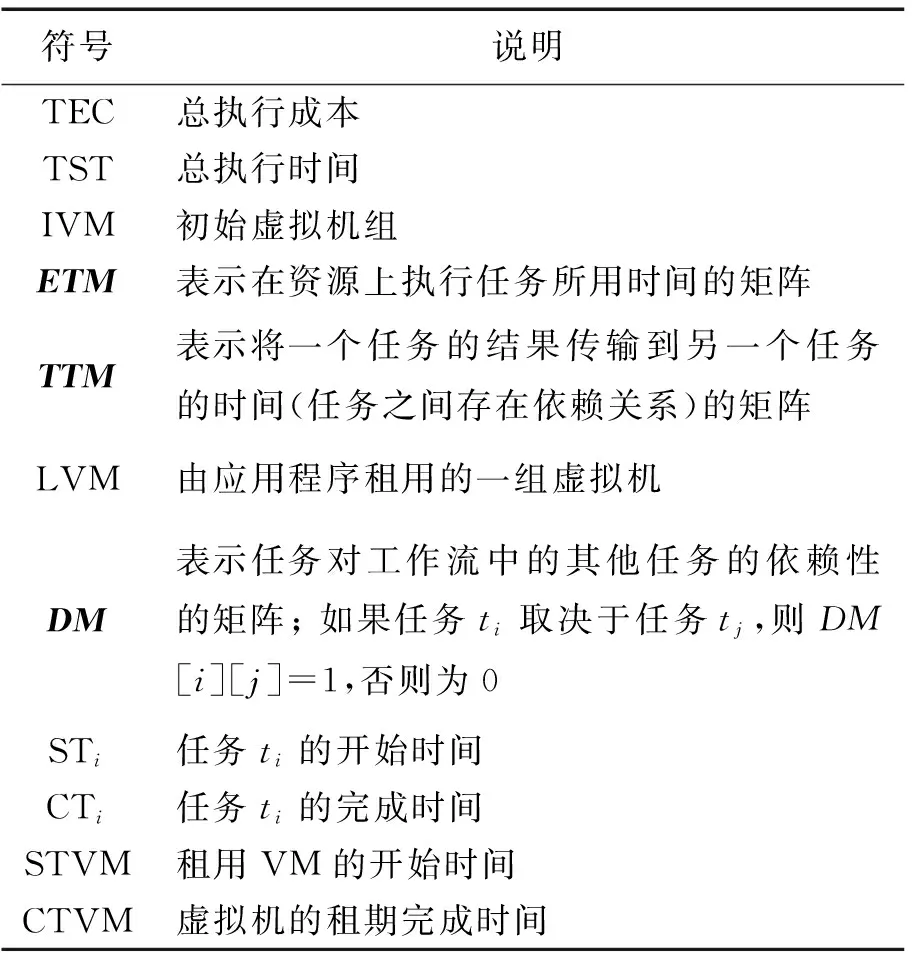
表3 符号说明Tab.3 Symbol description

算法伪代码如下。

输入：用户提交的工作流应用，设置初始虚拟机组。

输出：总执行成本和总执行时间。

1. 初始化参数TEC=0, TST=0, LVM=Φ: flag=0；

2. 计算时间ETM，TTM；

3. 添加依赖关系DM；

4. For 0 < id-1

i.初始化任务和虚拟机，令ti=T[i]，VM(i)= IVM[Mi]，flag=0

ii.for 0 < jd-1；//定义任务ti的开始时间

IfDM[i][j]==1,{flag=1; STi=max(STi,CTj,CTVM (VM(i))}

If flag==0 STi=CTVM(VM(i))

iii.在资源上执行任务所用时间exe_time=ETM(ti, VM(i))；

iv. for 0 < jd-1；//定义传送时间

IfDM[j][i]==1 and VM(j)< >VM(i)

Trans_time+=Trans_time+TTM[i][j]

v.任务在虚拟机上的总运行时间Tot_time (i, VM(i))=exe_time+trans_time

vi. CT(i, VM(i))=STi+ Tot_time (i, VM(i))；//任务的完成时间

vii. If VM(i)LVM, add it, STVM (VM(i))=STi；//租用VM的开始时间

viii. CTVM (VM(i))= Tot_time (i, VM(i))+STi；//虚拟机的租期完成时间

5. 计算每个VM的总执行成本和总执行时间，令cLVM；

i. TEC=TEC+((CTVM[c]-STVM[c])*Cost[c])

ii. if(CTVM[c]>TST)

该算法提供了需要为工作流租用的VM的数量。每个任务ti与一个虚拟机VM(i)相关联，VM(i)的开始和完成时间分别被给定为STVM和CTVM。此后，算法计算当前解决方案的总执行成本(TEC)和总执行时间(TST)。因此，对应于特定青蛙的调度方案由任务到VM的映射以及VM的开始和结束时间给出。

2.3 资源调度算法整体步骤

改进的SFLA和调度方案生成算法被组合以得到接近最优的调度。在改进的SFLA中，根据总执行成本来计算蛙的适应度，其通过使用上面给出的调度方案生成算法生成调度方案来评估。如果对应青蛙的调度时间超过最后期限，改进的SFLA用新的随机生成解替换该青蛙。以这种方式，改进的SFLA仅保留满足期限约束的调度方案。

步骤1利用调度方案生成算法产生工作流的原始调度；

步骤2通过改进的SFLA，保留满足期限约束的调度方案。

3 仿真分析

本文使用JAVA模拟器和3个不同大小的工作流来评估性能。每个模拟仿真进行25次，并且在SFLA和PSO算法中实现以作比较。控制参数如表4所示。

表4 控制参数Tab.4 Control parameters

假定从一个资源到另一个资源具有不同的任务执行时间[12]。工作流的最后期限是由对每个工作流执行的最小和最大执行时间的平均值得出。计算最大执行时间的方法是，租用最少时间的单个虚拟机，并在其上执行所有工作流任务[13-14]。通过对每个工作流任务使用一个最快类型的虚拟机来计算最小执行时间。

1)周期性参数“n”控制执行重建策略的频率，也就是最佳青蛙试图改善其位置的次数。n=1的值意味着最佳青蛙尝试在每次迭代中重新定位。本文进行了具有不同参数设置的一系列实验，最终确定了最佳参数组合。改进的蛙跳算法中，周期参数的取值为n=2，迭代次数定为50。

2)任务流的大小对总执行成本的影响。本研究在3种不同工作流程上进行：工作流1为Montage，工作流2为LIGO，工作流3为Cyber Shake。所有这些工作流具有不同的结构、不同的数据和计算特性。Montage工作流程是一个天文学应用程序，用于根据一组输入图像生成天空的自定义马赛克。大多数任务是I / O密集型，不需要高CPU处理能力。LIGO工作流程来自物理学领域，目的是检测引力波。此工作流主要是CPU密集型任务，需要大量内存。Cyber Shake用于通过生成合成地震图来区分地震危害，并且是具有高CPU和内存要求的数据密集型工作流。除了给出的3个应用工作流，再随机生成其他2个工作流：①具有少量任务(任务= 8)；②具有大量任务(任务= 150)。我们在仿真中设定云资源的时间为10，20和30单位，处理器统一设为4，使用的其他参数列于表5中。

表5 仿真参数Tab.5 Simulation parameters

图4描述了由PSO，SFLA和改进的SFLA获得的总执行成本。从结果中可以观察到，与PSO相比，SFLA能够将总执行成本平均降低约42%，改进的蛙跳算法平均降低约48%。

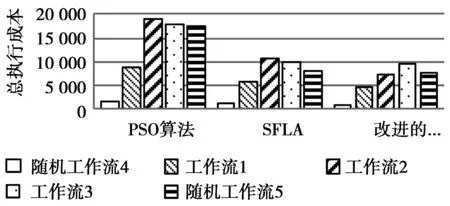
图4 总执行成本vs不同任务数的工作流Fig.4 Total execution costs vs workflow with different tasks

3)处理器数量对总执行成本的影响。本文进行了严格仿真来研究不同数量的资源对不同大小工作流程的影响。对于每个工作流，处理器的数量在1～10内选定；任务量的大小分别为100，200，300；处理器数量分别为 2， 4，6，8，10；最大迭代次数为50。仿真结果如图5所示。

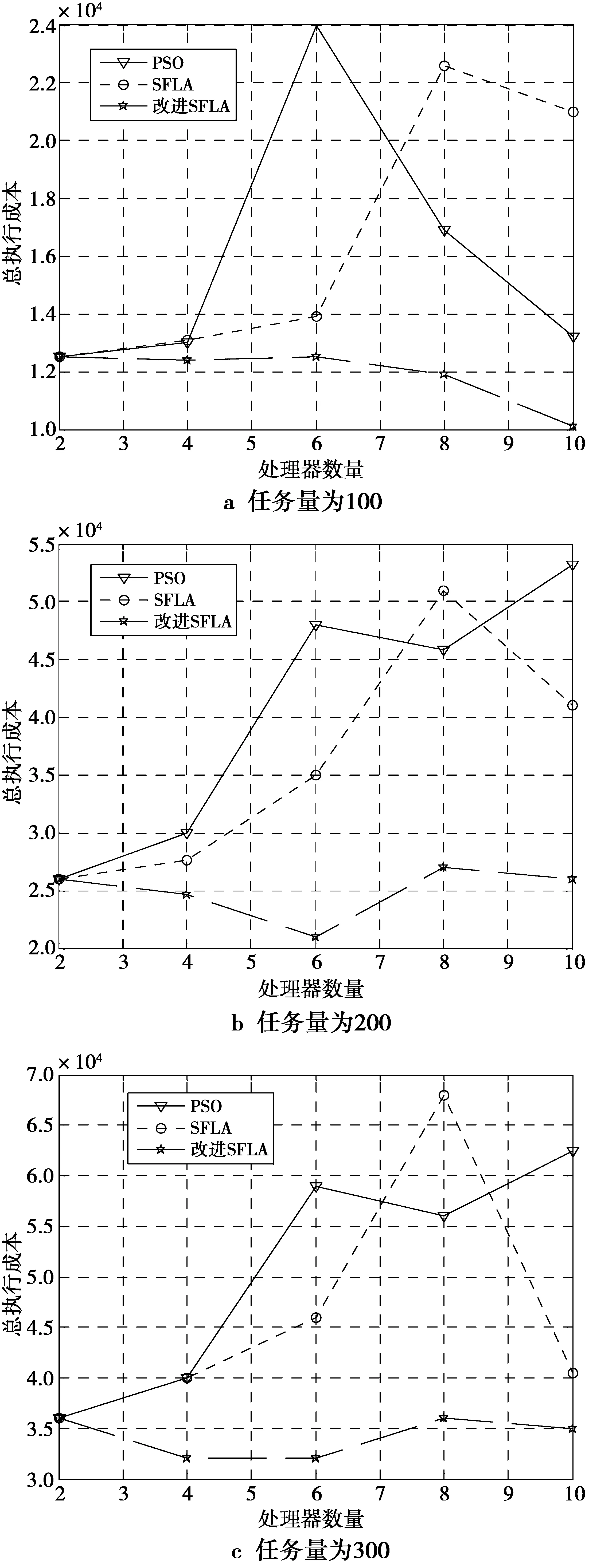
图5 总执行成本vs所使用的处理器的数量Fig.5 Total execution costs vs the number of processors used

从结果可以观察到，执行的时间随着用于工作流的资源数量的增加而增加。另外，可以看出，在某些情况下，PSO的性能优于SFLA，在其他情况下趋势逆转。然而，改进的蛙跳算法一直优于PSO和SFLA。在仿真期间，随着较高数量的资源被用于执行，总执行时间减少。这些结果没有列入，因为所有的时间规划都符合截止日期的限制。

4)算法的可扩展性评估。我们使用极大工作流的来验证算法的可扩展性，采用100个处理器，用于执行大小变化为300，500和1 000的随机工作流。极大工作流下的总执行成本比较如图6所示。

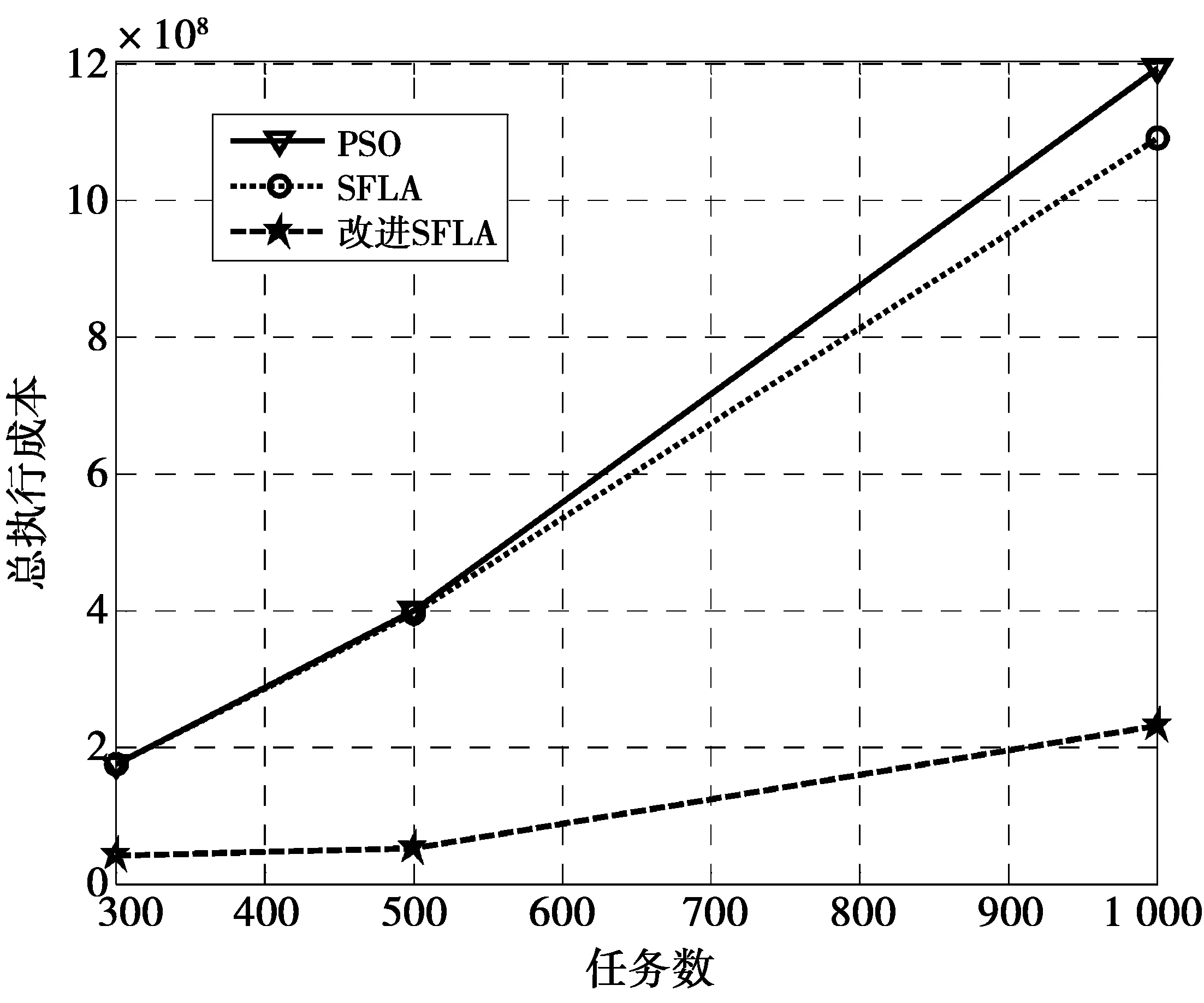
图6 极大工作流下的总执行成本比较Fig.6 Comparison of total execution costs under maximum workflow

从图6可以看出，随着工作流大小的增加，PSO和SFLA给出可比的性能。与PSO和SFLA相比，改进的SFLA将总执行成本平均降低了约78%，显示其巨大的性能优势。因此，本文所提算法是高度可扩展的，适于在IaaS云中执行较大的工作流应用。

5)不同算法的吞吐量比较。进行了仿真来研究不同数量的资源节点对吞吐量的影响。对于每个工作流，处理器的数量在1～10内选定，仿真结果如图7所示。

从图7中观察到，虽然处理器数目较少时，三类算法吞吐量相差不大。但是，随着处理器数目的增多，本文算法的优势体现出来，并且不断增强。这更适合于大数据时代的挑战，长远来看，本文算法的吞吐量更高。

6)关于鲁棒性和开销的推断。所提出的算法的鲁棒性可以从这样的事实推断，本文算法能够较好地满足具有不同数量的任务工作流的期限约束。此外，与PSO和SFLA相比，改进的SFLA能够将总执行成本降低高达78%，显示其良好的鲁棒性。另外，成本的减少会增加执行时间的开销，但是本文的算法对最小化执行成本是主要关注点，故而主要适用于优先考虑执行成本的情况。

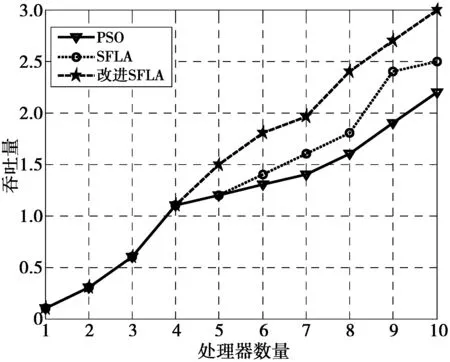
图7 不同算法的吞吐量比较Fig.7 Comparison of throughput of different algorithms

4 结 论

本文提出一种改进的蛙跳算法，用于云环境下的资源调度和调度。在满足指定目标约束的同时，优化工作流的总执行成本。对各种工作流进行了仿真，并且与SFLA和PSO算法的性能比较，仿真分析表明，改进的蛙跳算法在降低的工作流总体执行时间方面优于其他算法。

[1] ZOU D, XIANG Y, MIN G. Privacy preserving in cloud computing environment[J].Security & Communication Networks, 2016, 9(15):2752-2753.

[2] LI Y, TANG X, CAI W. Dynamic Bin Packing for On-Demand Cloud Resource Allocation[J]. IEEE Transactions on Parallel & Distributed Systems, 2016, 27(1):157-170.

[3] MA J, LI W, FU T, et al. A Novel Dynamic Task Scheduling Algorithm Based on Improved Genetic Algorithm in Cloud Computing[M].Berlin：Springer-Verlag , 2016:184-186.

[4] YOUNG L, MCGOUGH S, NEWHOUSE S, et al. Scheduling Architecture and Algorithms within the ICENI Grid Middleware[C]//RR Holman.UK e-science all hands meeting.Nottingham：Pergamon Press Ltd，2003:5-12.

[5] 贲可荣,张彦铎.人工智能[M].2版.北京：清华大学出版社, 2013：134-142.

BEN Kerong, ZHANG Yanduo. Artificial Intelligence. Second Edition[M].2nd.Beijing:Tsinghua University Press, 2013：134-142.

[6] ALRASHIDI M R, ELHAWARY M E. A survey of particle swarm optimization applications in electric power systems[J]. Evolutionary Computation, IEEE Transactions on, 2009, 13(4): 913-918.

[7] ZHU G Y, ZHANG W B. An improved Shuffled Frog-leaping Algorithm to optimize component pick-and-place sequencing optimization problem[J]. Expert Systems with Applications, 2014, 41(15):6818-6829.

[8] BOTTA A, DE DONATO W, PERSICO V, et al. Integration of Cloud computing and Internet of Things[J].Future Generation Computer Systems, 2016, 56(C):684-700.

[9] ZHANG Q, YU G U, YING X U, et al. Feature selection for SAR images using the hybrid intelligent optimization algorithm[J]. Journal of Remote Sensing, 2016，38(18)：110-119.

[10] EUSUFF M M, LANSEY K E. LANSEY, K. Optimization of Water Distribution Network Design Using the Shuffled Frog Leaping Algorithm. Journal of Water Resources Planning and Management[J].Journal of Water Resources Planning & Management, 2003, 129(3):210-225.

[11] JUVE G, CHERVENAK A, DEELMAN E, et al. Characterizing and profiling scientific workflows[J]. Future Generation Computer Systems, 2013, 29(3):682-692.

[12] KOZERA R, OKULICKADF, NOAKES L. Integrated Parallel 2D-Leap-Frog Algorithm for Noisy Three Image Photometric Stereo[C]//PR Jones.PSIVT 2015 Workshops. Berlin：Springer-Verlag，2016：73-87.

[13] 黄婷婷,梁意文.云工作流任务调度的模拟退火遗传改进算法[J].微电子学与计算机, 2016, 33(1):42-46.

HUANG Tingting, LIANG Yiwen.Improved Anomalous Improvement Algorithm for Task Scheduling of Cloud Workflow[J]. Microelectronics and Computer, 2016, 33(1): 42-46.

[14] FU X, YELIANG C, ZHU L, et al. Deadline based scheduling for data-intensive applications in clouds[J]. Journal of China Universities of Posts & Telecommunications, 2016, 23(6):8-15.

The National Natural Science Foundation of China(61302099)

Optimizationofcloudworkflowschedulingalgorithmbasedonreconstructionstrategy

LIN Haitao, JIANG Donghan

School of Electronic Engineering, Naval University of Engineering, Wuhan 430033, P.R. China)

In order to further improve the performance of the algorithm, this paper proposes an improved leapfrog algorithm, which is combined with the scheduling scheme to provide optimal scheduling for cloud workflow resource allocation. First of all, by means of joining the reconstruction strategy to improve the randomness of data the local search in the frog leaking algorithm the local optimal is effectively prevented. Secondly, we study the scheduling scheme generation algorithm, and get the optimal scheduling with the improved algorithm. Finally, the simulation experiment is carried out using Java simulator, and compared with the particle swarm optimization algorithm and the traditional frog leap algorithm. It is found that the proposed method can minimize the total execution cost while satisfying the longest deadline constraint.

frog leaping algorithm; resource scheduling; cloud workflow; reconstruction strategy

10.3979/j.issn.1673-825X.2017.06.017

2017-02-15

2017-06-05

姜栋瀚 457176001@qq.com

国家自然科学基金(61302099)

TN93

A

1673-825X(2017)06-0822-08

林海涛(1974 -)，男，山东潍坊人，副教授，博士，主要研究方向为网络规划与管理。E-mail：1174756267@qq.com。

姜栋瀚(1992 -)，男，山东烟台人，硕士研究生，主要研究方向为通信技术与网络。E-mail：457176001@qq.com。

(编辑：王敏琦)