基于最大相关波形延拓改进的EEMD方法

郭翠娟,李德冲,荣 锋,刘晓勇

(1.天津工业大学 电子与信息工程学院,天津 300387;2.天津工业大学 天津市光电检测技术与系统重点实验室,天津 300387)

基于最大相关波形延拓改进的EEMD方法

郭翠娟1,2,李德冲1,2,荣 锋1,2,刘晓勇1,2

(1.天津工业大学 电子与信息工程学院,天津 300387;2.天津工业大学 天津市光电检测技术与系统重点实验室,天津 300387)

针对经验模态分解(empirical mode decomposition，EMD)中出现的端点效应和模态混叠现象问题，提出了利用最大相关波形延拓改进聚合经验模态分解(ensemble empirical mode decomposition，EEMD)方法。利用最大相关波形法对原始信号的两端进行延拓，实现延拓数据在原信号边界处的平滑过渡，减小端点处包络线的拟合误差。针对EEMD中参数无法自动获取的问题，采用自适应EEMD对新信号进行分解，提高信号的分解精度。通过仿真分析和转子不平衡故障诊断实例研究表明，改进的EEMD方法不仅能够明显减少虚假模态分量、有效抑制模态混叠现象，而且较好地改善了端点效应引起的分解失真问题。同时与基于极值点对称延拓改进方法及基于镜像延拓改进方法相比，所提方法具有较高的分解精度。

聚合经验模态分解(EEMD)；端点效应；模态混叠；时频分析

0 引 言

经验模态分解(empirical mode decomposition，EMD)作为一种新的信号时频处理方法[1]，由于其具有较高的频率分辨率、良好的自适应性，使得其广泛应用于非平稳信号和非线性信号的分析，在机械故障诊断中也取得了很好效果[2-3]。但是EMD在分解过程中存在模态混叠现象、端点效应等问题，严重影响分析结果的准确性，制约着EMD在实际机械故障诊断中的应用。针对EMD分解过程中出现的模态混叠现象，宋立新等[4]通过EMD分解找到原信号中的不连续成分，并对除去该成分后的新信号重做EMD分解从而消除混叠现象，但结果会受到吉卜斯效应的影响。Li等[5]提出了利用小波进行信号预处理来滤除间断高频信号，然后再进行EMD分解，提高了分解效果，但是小波基的选择是一个难点。Wu等[6]利用白噪声的频谱均匀分布以及零均值的统计特性，提出了一种对小幅值白噪声和原始信号总体进行EMD分解的方法—聚合经验模态分解(ensemble empirical mode decomposition，EEMD)。虽然该方法很大程度上减少了无实际物理意义分量的产生，但是EEMD并未对EMD分解过程中端点处极值不确定的问题做有效处理，从而影响了EEMD对模态混叠的抑制效果[7]。在解决端点效应的问题上，李敏等[8]提出在原始信号2端点处进行对称性延拓，并结合信号序列加窗函数的方法，解决了信号包络拟合时的发散问题，但该方法对于非平稳信号分解效果较差。周龙宝等[9]提出神经网络延拓数据方法，有效解决了HHT(Hilbert-Huang trans from)中存在的端点效应问题，然而该方法需要较长的学习时间，效率较低。沈路等[10]直接利用端点附近的若干极值点对原始数据进行延拓，但并没有考虑信号内部极值点总体关系对信号延拓的影响。高强等[2]通过找到原始信号内部与端点处波形变化趋势最为相近的子波，并以该子波外侧数据作为端点处延拓数据的估计，使得分解结果没有出现明显的端点效应，但并未针对出现的模态混叠现象进行优化，使得经验模态分解后产生了很多无实际物理意义的分量。此外，还有最大Lyapunov指数拓延[11]、Volterra模型延拓[12]、多项式拟合[13]等针对端点处极值不确定的优化方法。这些方法的提出虽然一定程度上改善了EMD的分解效果，但它们在消除端点效应和模态混叠现象方面仍有不足[14]。因此，本文在分析EEMD分解过程中产生端点效应原理的基础上，提出一种利用最大相关波形延拓改进的EEMD方法，并进行了仿真信号和实测转子不平衡故障信号的验证研究。

1 方法的引入

1.1 EEMD方法

EEMD方法是EMD的一种改进方法。该方法通过给信号加入一定幅度的白噪声，利用白噪声频谱均衡分布的特点来均衡脉冲干扰等异常事件对信号的影响，较为理想地抑制了模态混叠造成的影响。由于每次EMD分解的白噪声是不同的，根据白噪声零均值的特性，当使用数量足够EMD分解的全体均值时，噪声会被抵消，从而使真实信号得以保留。

EEMD的具体流程图如图1所示。

图1 EEMD算法流程图Fig.1 Flow chart of EEMD algorithm

从EEMD算法流程图可以看出，该方法一共需要进行M次EMD分解。在每次分解前都需要在原始信号中加入随机的、相对独立的白噪声序列nm(t)，组成复合信号xm(t)=x(t)+T·nm(t)，T为白噪声幅值比例系数。每次分解得到I个本征模函数(intrinsic mode function，IMF)分量，最终通过求解M次对应的IMF分量均值作为EEMD分解得到的各IMF分量值。

EEMD方法需要2个重要参数：添加的白噪声幅值系数T和EMD执行总次数M。过大的噪声幅值会影响信号中高频成分的特性，导致分解出多余的分量并增大误差；噪声幅值过小的话，则不能有效抑制模式混叠影响。较大的M可以提高分解精度，但同时也会增加计算量。

Wu Zhaohua等[15]指出EEMD方法中EMD执行总次数M满足下面的统计规律

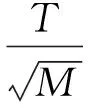
(1)

(1)式中：T为白噪声的幅值系数，也就是白噪声幅值标准差σ与原始信号的幅值标准差e0的比值系数；e为原始信号与EEMD分解得到的各IMF分量相对误差最大值。Wu等表明当e取1%时，分解效果已经非常理想。一般情况下取e=1%即可。因此，如果确定了T的取值，M的值便可以自动取得。本文采用文献[16]中T的取值标准T=X/4，X为EMD预处理分解得到的第一阶IMF分量与原始信号幅值标准差的比值。所以，只要预先设置好期望的e值，便可以自适应地获得T值和M值。该自适应算法的具体流程图如图2所示。

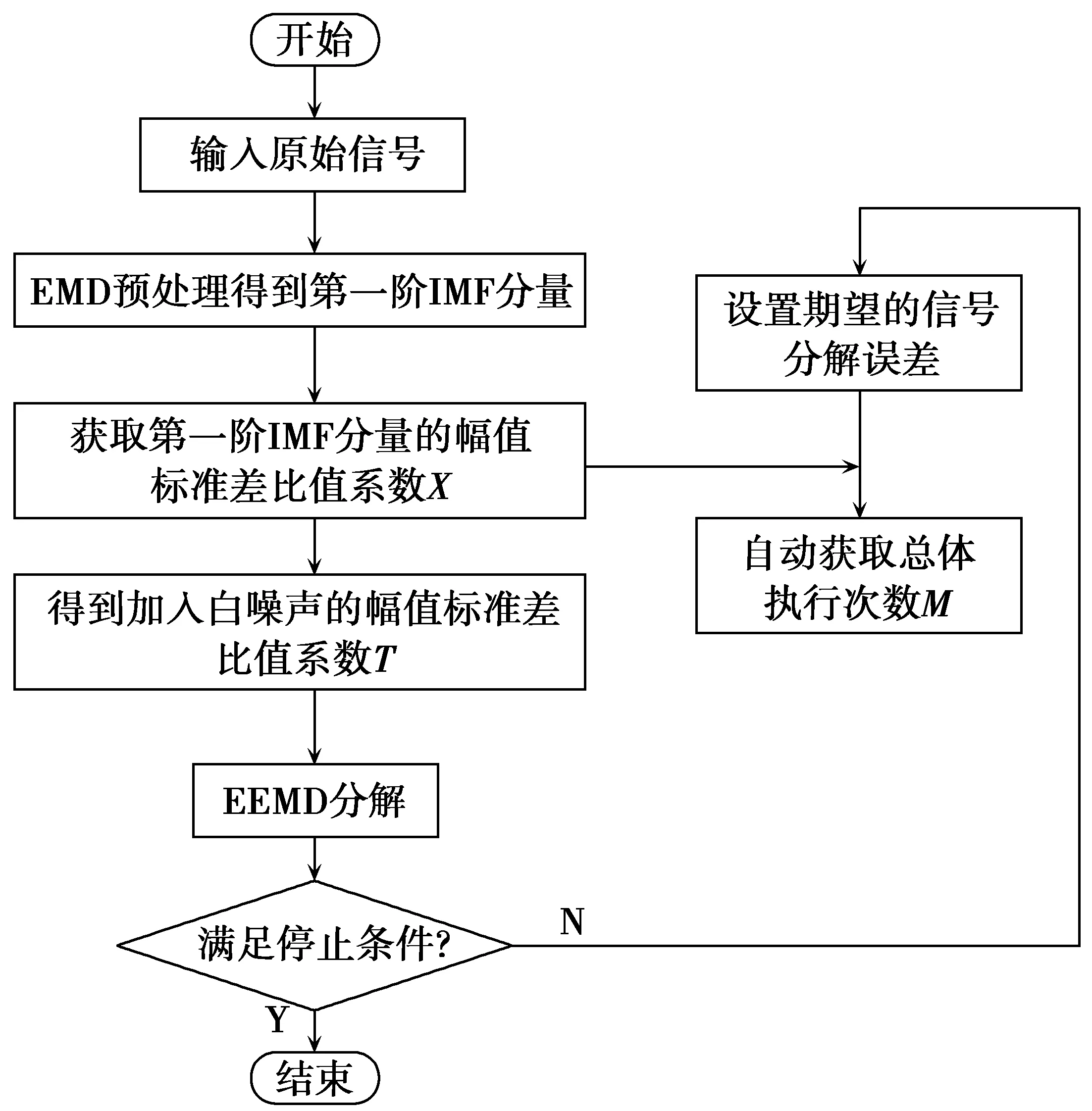
图2 自适应EEMD算法流程图Fig.2 Flow chart of adaptive EEMD algorithm

1.2 EEMD方法的端点效应和模态混叠问题

EEMD主要是通过多次的“筛选”过程来逐个解析得到IMF。在每一次的“筛选”过程中，要按照信号的上、下包络来得到信号的局部平均值。其中，针对信号的局部极大值和局部极小值采用3次样条插值算法可求得上、下包络。由于信号数据的长度有限，并且数据的2端点处的值不一定是极值，从而使得利用3次样条插值算法得到的上下包络在数据序列2端处有很大波动，而且这种波动在“筛选”过程中会逐级传递下去的，最终会干扰到整个数据序列，使得分解结果严重失真，造成端点效应。端点效应会使EMD分解产生许多虚假的IMF分量，同时造成同一IMF成分中包含不同的频率成分，严重影响EEMD方法抑制模态混叠的效果。

1.3 最大相关波形延拓法

最大相关波形延拓法(maximal correlation waveform extension，MCWE)的主要思想是通过定位信号内部与端点处波形相关系数最大的波形，然后截取出最相关波形外侧若干数据添加到端点处，从而获得端点处延拓的数据，并使得延拓的数据符合原信号内部的变化趋势。

具体步骤如下(以左端点为例，右端点类似)。

1)在信号的时域波形图中，设信号x(t)左端点为k0，过k0作一条水平的直线与信号的波形从左往右依次交于k1,k2,…,kn点；

2)以k0为起点，向右选取至少包含一个过零点、一个局部极大值点及一个局部极小值点的曲线段L0，并计算其数据长度为l0；

3)分别以k1,k2,…,kn为起点，取数据长度为l0的曲线段L1,L2,…,Ln；

4)分别求L0与各曲线段L1,L2,…,Ln的相关系数Ri，即

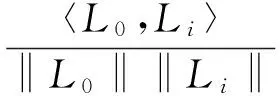
(2)

5)找到最大相关系数所对应的曲线段Li并定位其数据起点，取数据起点左边包含多个极值点的曲线段La作为左端点向外的数据延拓。其中，曲线段La的长度为la，可根据实际情况自行决定。

2 利用最大相关波形延拓改进的EEMD

本文将最大相关波形延拓和EEMD结合，提出了基于最大相关波形延拓改进EEMD的方法。首先通过最大相关波形延拓法对原始信号两端点处数据进行拓延；然后，针对包络线拟合中存在的“过冲”和“欠冲”表征，对3次样条插值法进行优化；最后，用自适应EEMD方法对新数据信号进行分解，并将截去延拓部分的分解结果作为最终数据结果，从而有效抑制端点效应和模态混叠现象。具体步骤如下。

1)对原始信号x(t)进行最大相关波形延拓，使得端点效应外移到延拓后的数据2端，从而减小端点效应对原始信号的影响；

2)根据自适应EEMD方法确定白噪声的幅值比例系数T和总体平均次数M，并将M组均值为零、幅值比例系数相等的随机白噪声序列加入到延拓后的信号中，得到M个随机的复合信号xm(t),m=1,2,…,M;

3)利用EMD算法对M个复合信号xm(t)进行分解，得到M组IMF分量{[C11,C21,…,CI1]，[C12,C22,…,CI2]，…，[C1M,C2M,…,CIM]}和M个余量[RI1,RI2,…,RIM]，其中每组共有I个IMF分量。在EMD分解过程利用优化过的3次样条插值算法：首先，用直线段分别将信号的极大值点和极小值点连接起来，形成上、下包络线段；其次，利用上、下包络线段求出2者的平均包络线段；最后，用3次样条曲线拟合平均包络线段得到信号的平滑均值包络；

4)得到M组IMF分量相应的均值{C1,C2,…,CI}和M个余量的均值Res，则x(t)可以表示为

(3)

(3)式中

(4)

5)原始信号x(t)的最终的分解结果为截断延拓数据后剩余的数据序列。

该改进的EEMD方法在继承自身抑制模态混叠优势的基础上，利用MCWE方法延长原始数据，来减小端点效应对分解结果的影响。

文献[1]提出使用IMF分量间的正交性指标(index of orthogonality，IO)作为EMD分解效果的评价标准。EEMD实质上是由多次EMD组成的，所以本文采用该标准评价改进EEMD方法的分解精度。IO值越小，相应的分解精度越高。

(5)

(5)式中：L为数据长度；I为分解得到的IMF分量的总个数。

3 仿真试验分析

为了验证EEMD改进方法的性能，设置一个仿真信号x(t)，解析表达式为

x(t)=cos[80πt+0.5sin(40πt)]+cos(360πt)

(6)

信号x(t)由幅值为1、频率为180 Hz的调幅信号a和基频为40 Hz，调制频率为20 Hz的调频信号b加合构成。采样频率为1 000 Hz，采样时间为0.4 s，得到如图3所示时域波形。

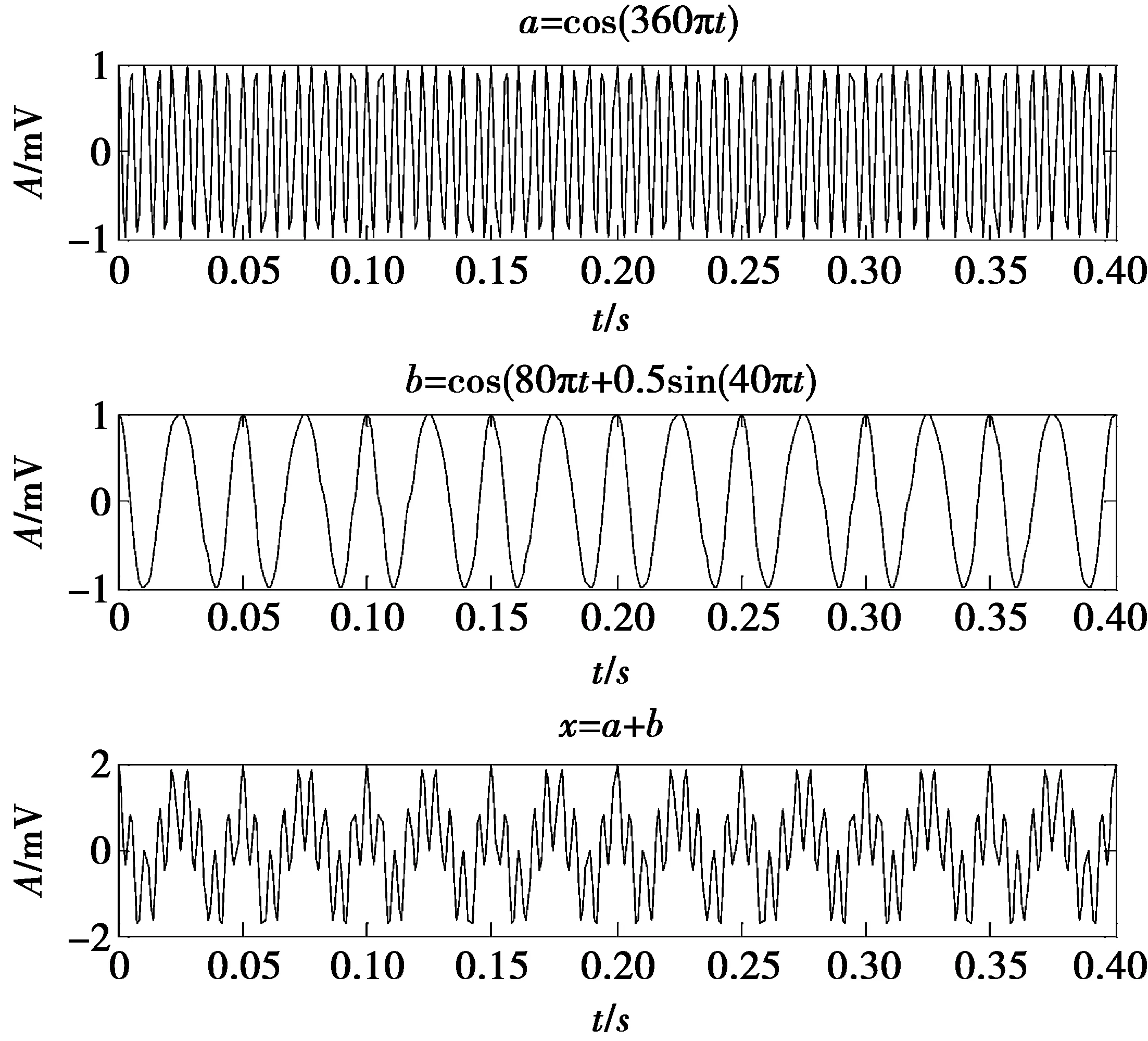
图3 仿真信号及其构成分量Fig.3 Simulation signal and its components

用基于MCWE改进的EEMD方法对仿真信号进行分解。首先应用MCWE将原始信号向2端各延拓50个点；然后设置e值为1%，则根据自适应EEMD获取该仿真信号高频成分的幅值标准差与原始信号幅值标准差比值系数为0.705，那么加入白噪声的幅值标准差比值系数为0.176，总体平均次数为310；最后截去EEMD分解后数据2端延拓的50个点，得到图4所示的3阶IMF分量和1阶余量Res。从图4中可以看出，各阶分量波形端点处没有发散现象。第1阶IMF比较理想地还原了仿真信号中频率为180 Hz的调幅信号；第2阶IMF分量与仿真信号中的调频成分相对应，其波形的间距有明显的变化，表现出显著的调频特性。前2阶IMF分量与仿真信号中对应成分基本一致，且端点处没有波动现象产生。尽管分解结果多出了原信号中没有的分量IMF3和余量Res，但其幅值较小，可忽略不计，表明改进的EEMD方法高质量地分离出仿真信号中各个组成成分，抑制了混叠效应。

图5为经改进后的EEMD分解仿真信号得到的Hilbert时频谱。由图5可见，仿真信号有2个频率成分：一个是近似平稳的180 Hz频率成分；另一个是跟随采集点数做近似余弦波形摆动的频率成分，基频大约为40 Hz，上下摆动最大频率为20 Hz，清晰地还原了仿真信号的调制特性。

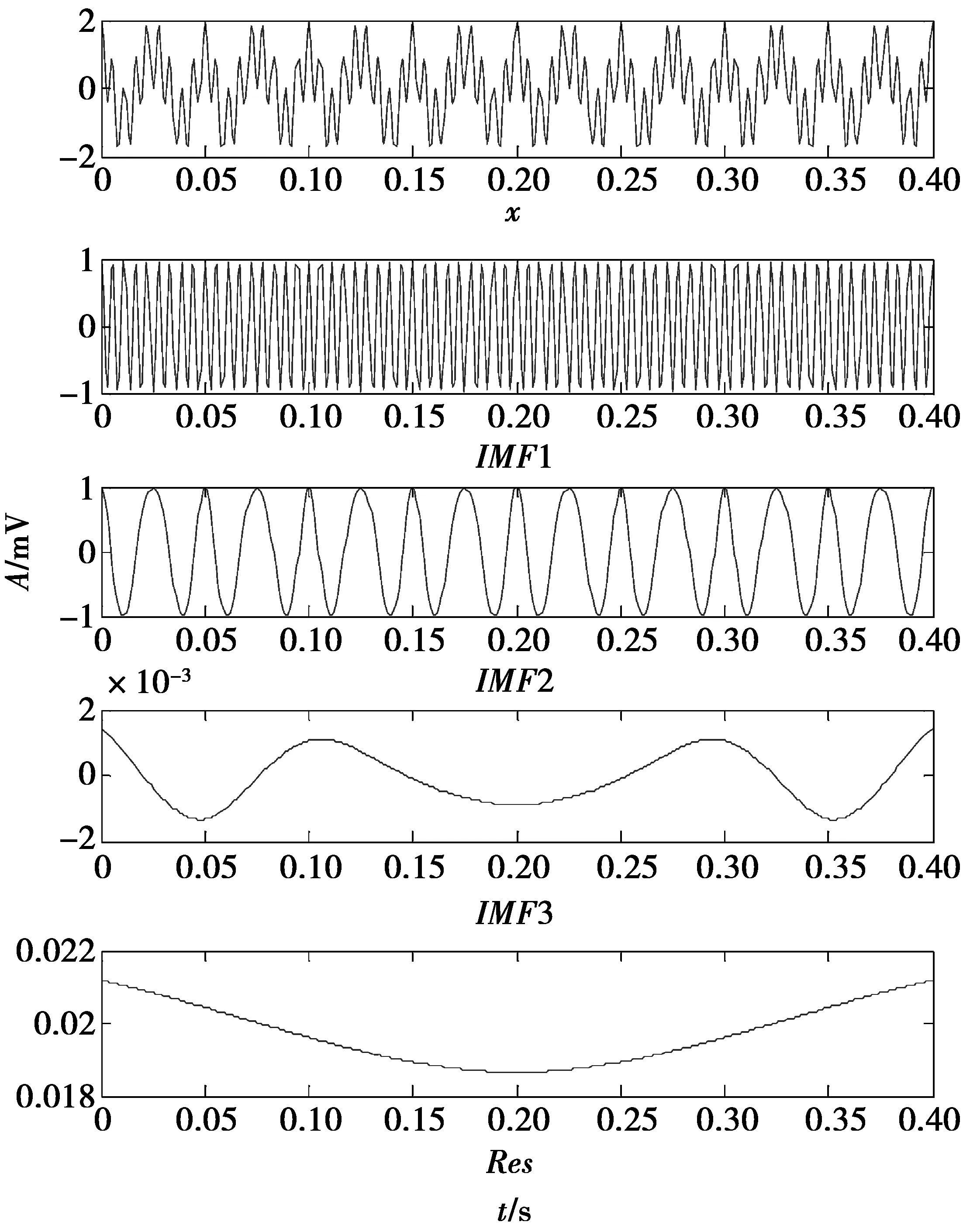
图4 改进EEMD方法的分解结果Fig.4 Decomposition results of the improved EEMD

图5 改进的EEMD分解的Hilbert时频谱Fig.5 Hilbert spectrum of the improved EEMD

为了验证改进EEMD方法的效果，分别用原始EMD和EEMD对仿真信号进行分析，得到图6和图7所示的时频谱。其中原始EEMD加入的白噪声幅值比例系数和总平均次数与本文改进EEMD方法中对应参数保持一致。对比相应结果图，利用EMD分解得到的Hilbert时频谱频率成分杂乱，有较多的虚假低频分量，在180 Hz频率2端处出现大范围的发散现象，这是由于端点效应和模态混叠的影响。利用EEMD分解得到的时频谱减少了虚假分量，表明EEMD有消除模态混叠的作用。但是由于端点效应的存在，使得得到的时频谱2端存在飞翼现象，模糊了特征频率，同时也影响了EEMD抗混频的效果。改进的EEMD方法分解得到的时频谱频率成分层次分明，分辨率高，基本没有虚假模态分量，两侧端点处几乎没有产生波动，说明改进的方法不仅有效消除了模态混叠现象，而且很好地解决了EMD和EEMD分解中的端点波动问题。

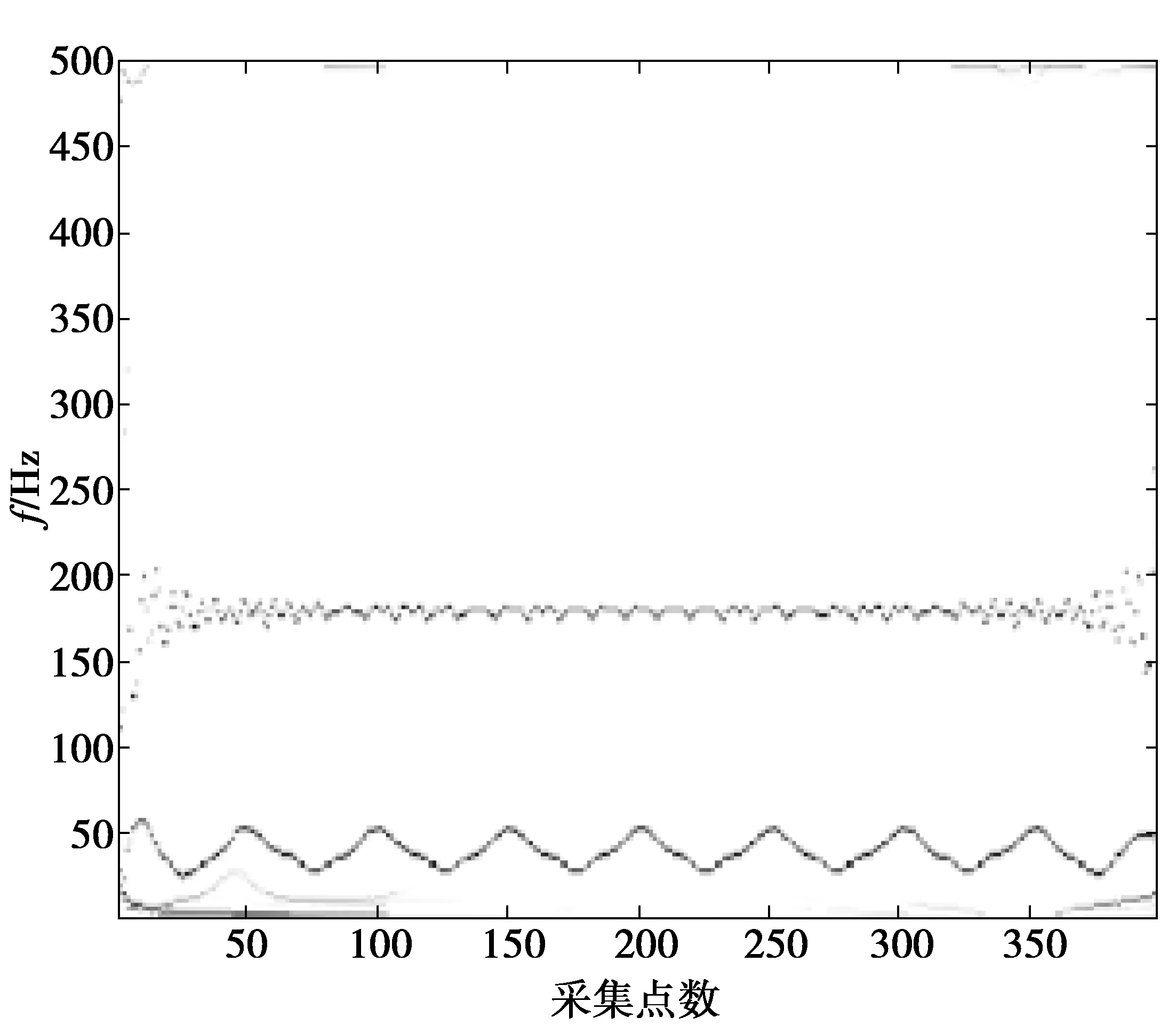
图6 仿真信号EMD分解的Hilbert时频谱Fig.6 Hilbert spectrum of EMD

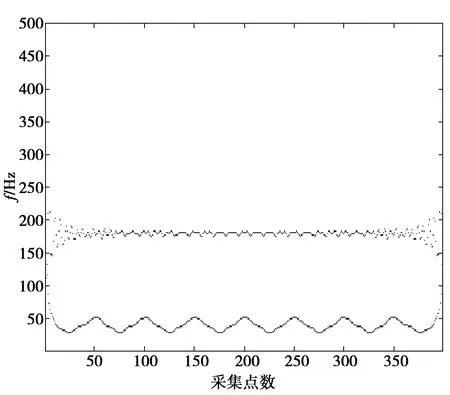
图7 仿真信号EEMD分解的Hilbert时频谱Fig.7 Hilbert spectrum of EEMD

为了更好地衡量3种方法的分解效果，计算相应的IO值，其结果对比如表1所示。

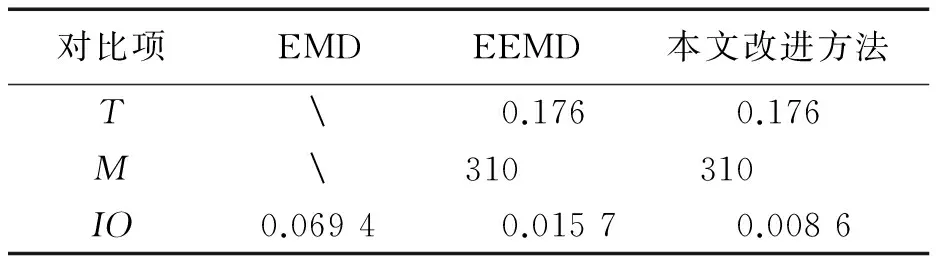
表1 3种分解方法结果对比Tab.1 A comparison between results of three decomposition methods

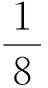
4 实测振动信号分析

为了分析本文提出的基于最大相关波形延拓改进EEMD方法的实用性，对东华DHRMT双跨转子实验平台的一组转子的实测数据进行分析。实验前人为制造转子不平衡故障。调节转子转速为1 025 r/min，则转子旋转频率为17.1 Hz。采样频率为1 kHz。选取采样时间为2.5 s，共2 500个采样数据点进行分析，得到如图8所示的转子振动信号的时域波形。

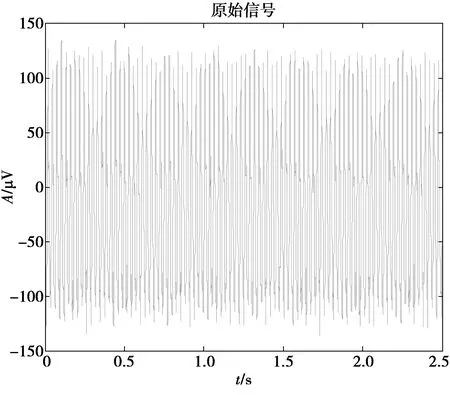
图8 实测振动信号Fig.8 Measured vibration signal

同样，首先应用MCWE向原始信号2端各延拓50个点；然后，将e的值设置为1%，则根据自适应性EEMD可自动获取该仿真信号高频成分的幅值标准差与实际信号幅值标准差比值系数为0.38，则加入白噪声的幅值标准差比值系数为0.095，总体平均次数90；最后截去EEMD分解后数据2端延拓的50个点，得到图9所示的6阶IMF分量和1阶余量。其中，IMF5为基频分量，表示转子的基频成分(约17.1 Hz)，波形为调频正弦波，幅值较小，波形2端并未出现大幅度摆动现象。IMF3和IMF4分别对应于转子频率的3倍频和2倍频分量，二者的幅值均高于基频幅值，尤其以2倍频最为明显。IMF6为0.5倍频分量，幅值较小。这些特性符合不平衡故障特征，而且三者的波形在端点处较为平稳，物理意义相对清晰。IMF1和IMF2为高频谐波成分，数据2端有轻微波动现象。因此，改进方法分解得到的各频率分量物理意义较为直观，端点效应不突出。

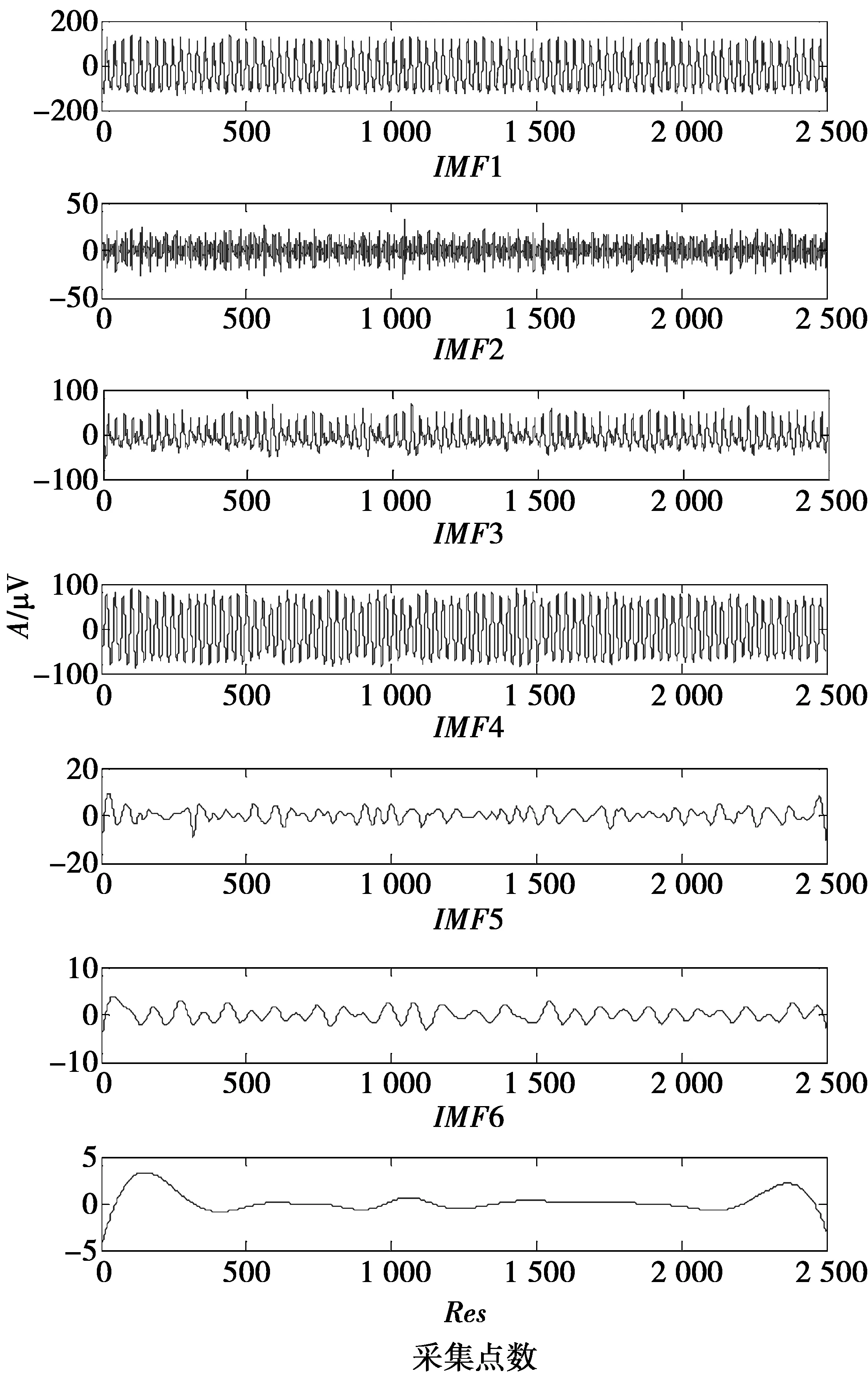
图9 基于最大相关波形延拓改进的 EEMD分解结果Fig.9 Decomposition results of improved EEMD method based on MCWE

为进一步验证本文所提方法的有效性，利用不同延拓方法改进的EEMD分解实测信号并得到对应的时频谱。这些方法均采用相同的白噪声幅值系数和总执行次数。各方法得到的时频谱结果分别如图10—图13所示。从图10—图13中可以看出，本文提出的EEMD改进方法得到的Hilbert时频谱清晰地描绘了基频的调频现象，基频、倍频等分界明显，虚假分量较少，频率相近的成分在端点处没有出现明显的交叉重叠，有较好的抑制端点效应效果。

原始EEMD获得的Hilbert谱端点发散严重，虚假频率分量较多，主要是端点效应影响了EEMD抑制模式混叠的效果。基于极值点对称延拓改进EEMD分解结果的Hilbert谱以及基于镜像延拓改进的EEMD分解结果的Hilbert谱相对原始EEMD得到的Hilbert谱谱线清楚，减少了虚假分量的产生，但由于端点效应抑制效果不是特别理想，依然存在部分频率成分交叉现象。

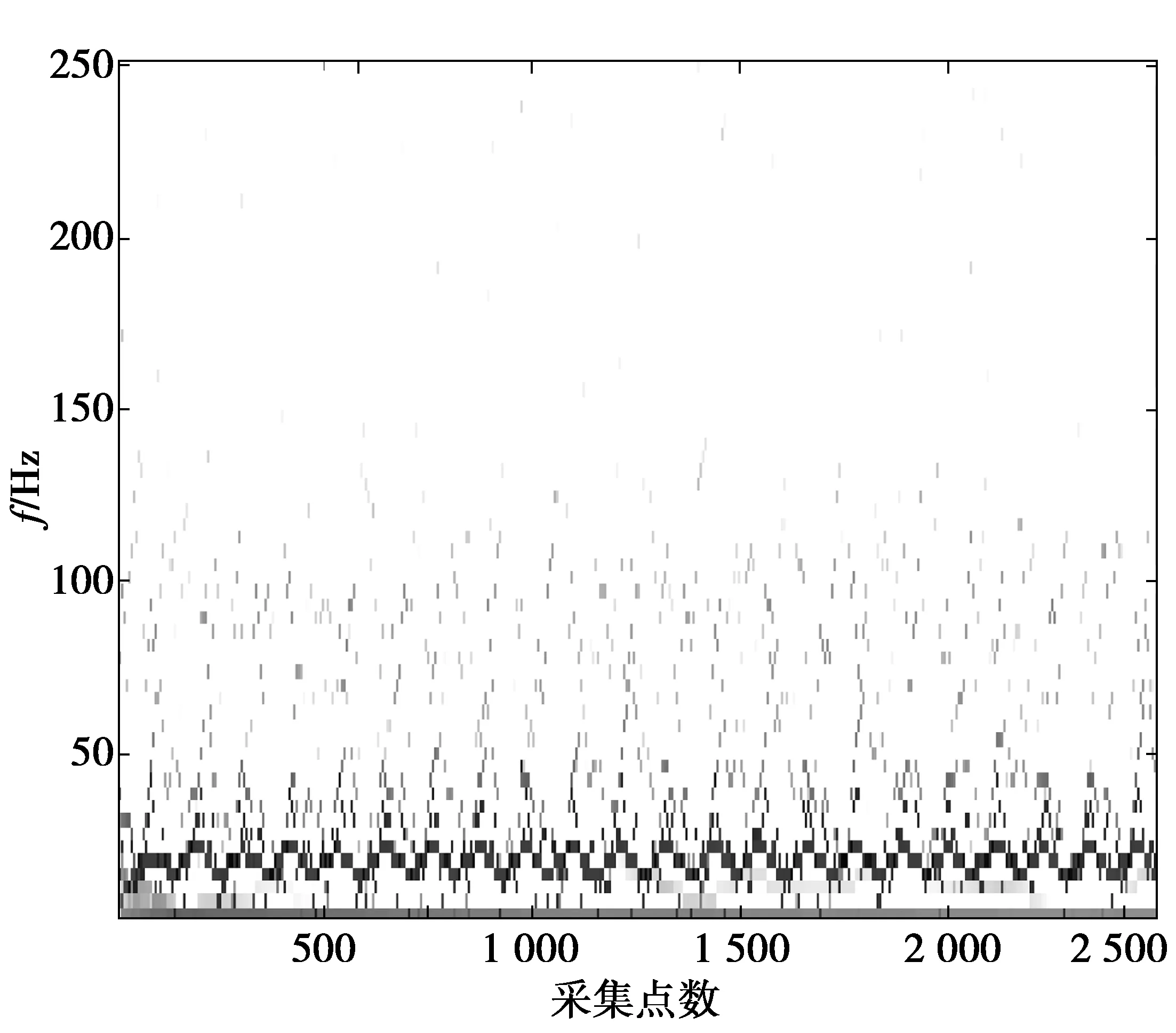
图10 基于最大相关波形延拓改进EEMD 分解的Hilbert时频谱Fig.10 Hilbert spectrum of improved EEMD method based on MCWE

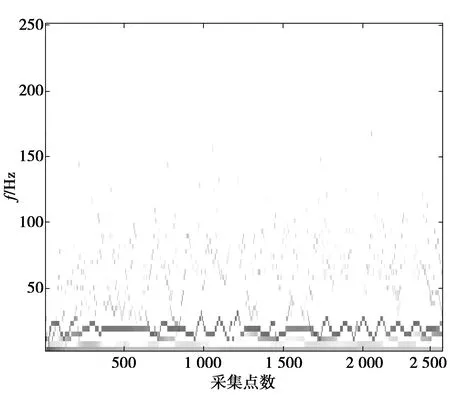
图11 EEMD分解的Hilbert时频谱Fig.11 Hilbert spectrum of EEMD

图12 基于极值点对称延拓改进的EEMD 分解的Hilbert时频谱Fig.12 Hilbert spectrum of improved EEMD method based on symmetrical extrema extension

计算各方法对应的IO值，如表2所示。

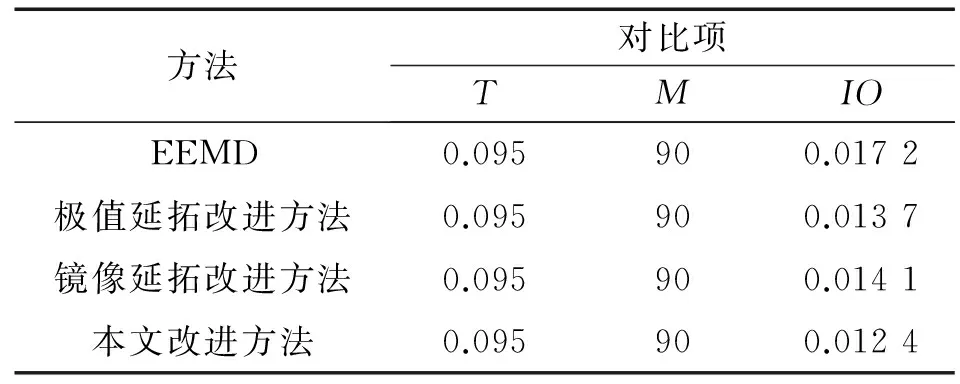
表2 不同方法正交性指标结果对比Tab.2 A comparison between the IO results of different methods

可以看出，本文所提改进方法相比于其他方法有较好的精确度，从而验证了本文改进方法在抑制端点效应和模态混叠方面有一定的优势。

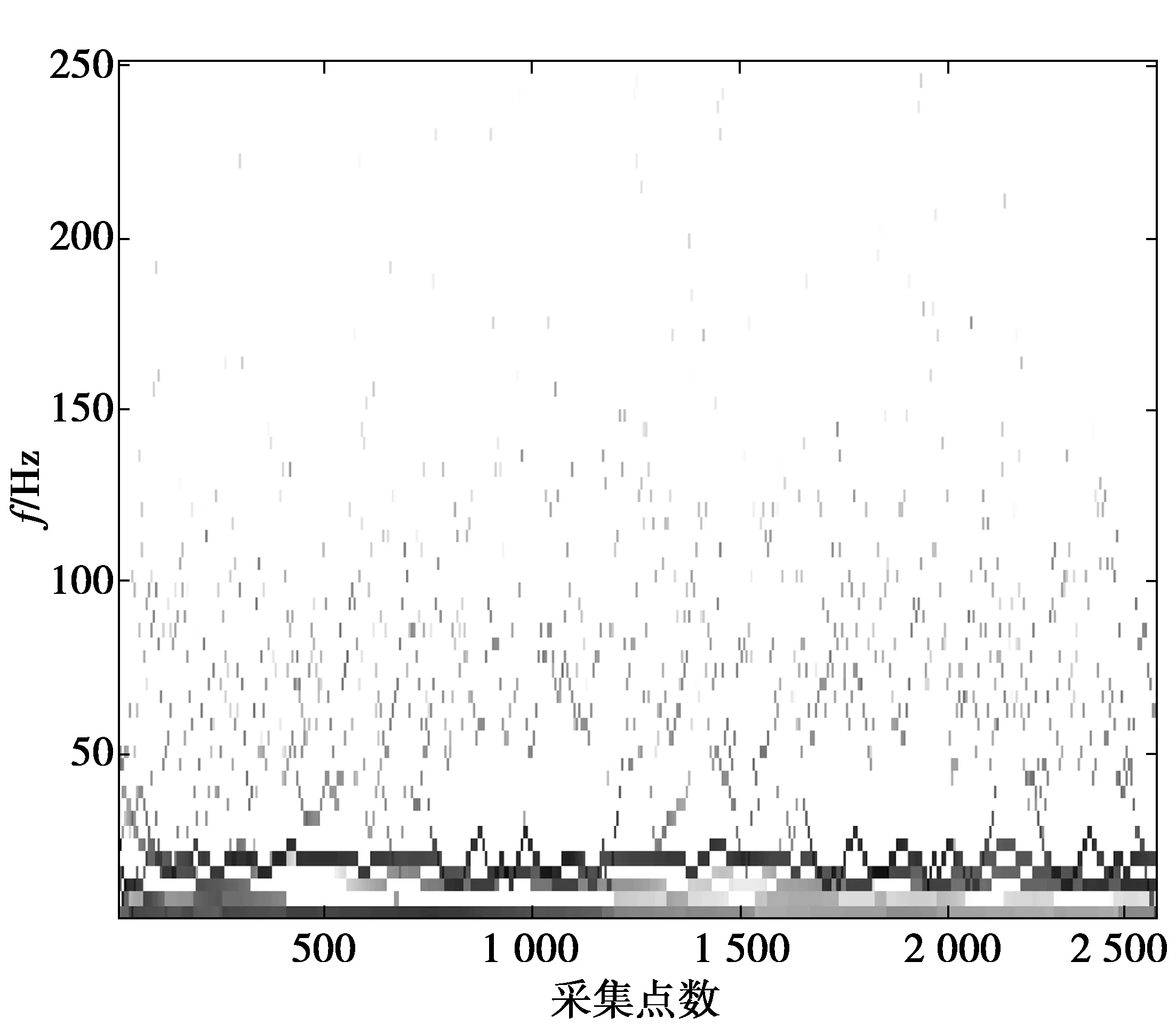
图13 基于镜像延拓改进的EEMD分解的 Hilbert时频谱Fig.13 Hilbert spectrum of improved EEMD method based on mirror extension

5 结 论

为了解决EMD分解中存在的端点效应和模态混叠问题，提出了利用最大相关波形延拓改进EEMD方法。该改进方法首先依据信号边界处的波形特征，找到信号内部与边界处波形相关性最大的波形，并以其外侧部分数据对原数据两端进行延拓；然后采用自适应EEMD算法自动获取添加白噪声幅值系数和EMD总执行次数对新信号进行分解。用改进的EEMD方法对仿真数据和实测振动信号进行分析，研究表明该方法能够明显减少虚假模态分量，有效抑制了模态混叠现象和端点效应，同时提高了分解精度，有很好的应用价值。

[1] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceeding of the Royal Society A Mathematical Physical & Engineering Sciences, 1998, 454(1): 903-995.

[2] 高强,段晨东,赵艳青,等.基于最大相关波形延拓的经验模式分解端点效应抑制方法[J].振动与冲击,2013,32(2):62-66.

GAO Qiang, DUAN Chendong, ZHAO Yanqing, et al. A maximal correlation waveform extension method for end effects reduction of empirical mode decomposition[J]. Journal of Vibration and Shock, 2013, 32(2): 62-66.

[3] LEI Yaguo, LIN Jing, HE Zhengjia, et al. A review on empirical mode decomposition in fault diagnosis of rotating machinery[J]. Mechanical Systems & Signal Processing, 2013, 35(1-2): 108-126.

[4] 宋立新,王祁,王玉静,等.具有间断事件检测和分离的经验模态分解方法[J].哈尔滨工程大学学报,2007,28(2):178-182.

SONG Lixin, WANG Qi, WANG Yujing, et al. Empirical mode decomposition method with intermittency test and separation[J]. Journal of Harbin Engineering University, 2007, 28(2): 178-182.

[5] LI Helong, YANG Lihua, HUANG Daren. The study of intermittency test filtering character of Hilbert-Huang transform[J]. Mathematics & Computers in Simulation, 2005, 70(1): 22-32.

[6] WU Z,HUANG N.Ensemble empirical mode decomposition:a noise assisted data analysis method[J].Advances in Adaptive Data Analysis,2009,1(1):1-41.

[7] 陈仁祥,汤宝平,吕中亮.基于相关系数的EEMD转子振动信号降噪方法[J].振动、测试与诊断,2012,32(4):542-545.

CHEN Renxiang, TANG Baoping, LV Zhongliang. Ensemble empirical mode decomposition de-noising method based on correlation coefficients for vibration signal of rotor system[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(4): 542-545.

[8] 李敏,程珩,张斌.EMD端点效应的处理方法研究[J].太原理工大学学报,2009,40(6):579-581.

LI Min, CHENG Heng, ZHANG Bin. Study on the method dealing with the end effect of EMD[J]. Journal of Taiyuan University of Technology,2009,40(6):579-581.

[9] 周龙宝,马景辉,李强.GA和RBF神经网络的Hilbert. Huang变换端点问题研究[J].计算机测量与控制,2012,20(2):447-450.

ZHOU Longbao, MA Jinghui, LI Qiang. Research of end effects in Hilbert-huang transform based on geneti algorithm and RBF neural network[J]. Computer Measurement & Control, 2012, 20(2): 447-450.

[10] 沈路,周晓军,张志刚,等.Hilbert-Huang变换中的一种端点延拓方法[J].振动与冲击,2009,28(8):168-174.

SHEN Lu,ZHOU Xiaojun,ZHANG Zhigang,et al.Boundary-extension method in Hilbert-Huang transform[J].Journal of Vibration & Shock,2009,28(8):168-174.

[11] 蔡艳平,李艾华,张玮,等.HHT端点效应的最大Lyapunov指数边界延拓方法[J].仪器仪表学报,2011,32(6):1330-1336.

CAI Yanping, LI Aihua, ZHANG Wei, et al. HHT end effect processing method based on maximum Lyapunov index boundary extension model[J]. Chinese Journal of Scientific Instrument, 2011, 32(6): 1330-1336.

[12] QIU Yan,WU Yafeng,LI Ye.Applying EMD decomposition of the Volterra model to extact mechanical fault feature[J].Journal of Vibration & Shock,2010,29(6):59-61.

[13] 刘慧婷,张旻,程家兴.基于多项式拟合算法的EMD端点问题的处理[J].计算机工程与应用,2004,40(16):84-86.

LIU Huiting, ZHANG Min, CHENG Jiaxing. Dealing with the end issue of EMD based on polynomial fitting algorithm[J]. Computer Engineering and Applications, 2004, 40(16): 84-86.

[14] 张梅军,陈灏,曹勤,等.基于SVM信号延拓的改进的EEMD方法[J].振动、测试与诊断,2013,33(1):93-97.

ZHANG Meijun, CHEN Hao, CAO Qin, et al. The improved EEMD method based on SVM signal continuation[J]. Journal of Vibration, Measurement & Diagnosis，2013, 33(1): 93-97.

[15] WU Zhaohua, HUANG N. A study of the characteristics of white noise using the empirical mode decomposition method[J]. Proceeding of the Royal Society A Mathematical Physical & Engineering Sciences, 2004, 460(2046): 1597-1611.

[16] 陈略,唐歌实,訾艳阳,等.自适应EEMD方法在心电信号处理中的应用[J].数据采集与处理,2011,26(3):361-366.

CHEN Lue,TANG Geshi,ZI Yanyang,et al.Application of adaptive ensemble empirical mode decomposition method to electrocardiogram signal processing[J].Journal of Data Acquisition & Processing,2011,26(3):361-366.

s：The National Natural Science Foundation of China(61405144); The Natural Science Foundation Project of Tianjin (15JCQNJC42100)；The Science and Technology Special Commissioner Project of Tianjin(16JCTPJC48100，16JCTPJ47200)

AnimprovedEEMDmethodbasedonmaximalcorrelationwaveformextension

GUO Cuijuan1,2, LI Dechong1,2, RONG Feng1,2, LIU Xiaoyong1,2

1.School of Electronics and Information Engineering, Tianjin Polytechnic University, Tianjin 300387, P.R. China;2.Tianjin Key Laboratory of Optoelectronic Detection Technology and Systems, Tianjin Polytechnic University, Tianjin 300387, P.R. China)

Aiming at the existing problems of end effects and mode mixing in EMD, an improved EEMD method based on MCWE(maximal correlation waveform extension) is proposed. Firstly, MCWE is used to achieve a smooth transition at the junction of an original signal and its extension and reduce the error of envelope near the ends of data. Secondly, in order to solve the problem that the parameters can not be obtained automatically in EEMD, the adaptive EEMD is used to decompose the new signal to improve the decomposition accuracy. Simulation results and rotor unbalance fault diagnosis examples show that the proposed new method not only can reduce false components and eliminate mode mixing in EMD, but also improve the decomposition distortion caused by end effect effectively. At the same time, it has higher decomposition accuracy compared with the improved EEMD method based on symmetrical extrema extension and the improved EEMD method based on mirror extension.

ensemble empirical mode decomposition (EEMD); end effects; mode mixing; time-frequency analysis

10.3979/j.issn.1673-825X.2017.06.010

2016-11-21

2017-09-23

荣 锋 471913480@qq.com

国家自然科学基金(61405144); 天津市自然科学基金(15JCQNJC42100)；天津市科技特派员项目(16JCTPJC48100，16JCTPJ47200)

TN911.7；TH165.3

A

1673-825X(2017)06-0768-08

郭翠娟(1975 -)，女，河北任丘人，博士、副教授。主要研究方向为旋转机械故障诊断和通信设备设计等。E-mail: guocuijuan@tjpu.edu.cn。

(编辑：张 诚)