一种任意比例LTS技术在DG-FETD中的应用

李 敏，沈微微，叶晓东，杨逸婷

(1.宿迁学院信息工程学院，江苏 宿迁 223800；2.南京邮电大学 电子与光学工程学院，南京 210033；3.南京理工大学 电子工程与光电技术学院，南京210094)

一种任意比例LTS技术在DG-FETD中的应用

李 敏1,2，沈微微2，叶晓东3，杨逸婷3

(1.宿迁学院信息工程学院，江苏 宿迁 223800；2.南京邮电大学 电子与光学工程学院，南京 210033；3.南京理工大学 电子工程与光电技术学院，南京210094)

不连续伽辽金时域有限元法(discontinuous Galerkin-finite element time domain，DG-FETD)便于处理多尺度电磁问题，但是由于精细结构或高介电参数媒质的存在，考虑到稳定性条件，整体时间步长的选取会受到最小剖分尺寸的影响，导致计算效率降低。针对该问题，在传统局部时间步长(local time stepping，LTS)技术的基础上提出一种基于蛙跳格式的任意比例LTS技术，该方法在求解多尺度问题时，减少了迭代所需时间，提高了不同时间步长选取的灵活性，同时随着未知量增加，其优势更加明显，结合数值算例，验证了该方法的正确性和有效性。

不连续伽辽金；多尺度；局部时间步长

0 引 言

近几十年来，时域有限元法(finite element method)因其便于模拟复杂外形及复杂媒质的特点，在计算电磁学中得到了越来越多的关注[1-2]。作为一种时域方法，时域有限元法具有可进行瞬时分析和宽带特性分析的优势，然而，其在每个时间步长都需要直接或迭代求解一个大型的矩阵方程组，尤其针对于多尺度电磁问题，是十分消耗计算资源和时间的，因此，时域不连续伽辽金法(discontinuous Galerkin time domain method)被提出，以便提高其计算效率和计算能力[3-4]。1973年不连续伽辽金有限元方法(discontinuous Galerkin finite element method, DG-FEM)最早由美国国家重点实验室的W.H.Reed和T.R.Hill[3]提出，它既可以像有限元法一样对目标模型进行非结构网格剖分，又可像有限体积分法一样单元之间采用数值通量[4](numerical flux)来传递。而不连续伽辽金时域有限元方法(discontinuous Galerkin-finite element time domain，DG-FETD)可以获得块对角特性的质量矩阵，对大型稀疏矩阵可直接求逆运算，同时易于并行计算，可处理非共形网格和使用分段连续基函数的特点。1999年，M.Y.Hussaini讨论分析了不连续伽辽金波传播问题；2014年，QIANG Ren和QING Huoliu等[5-6]讨论分析了基于EB的SETD-FETD结合的不连续伽辽金方法。

针对多尺度问题中DG-FETD稳定性受最小剖分尺寸影响导致整体时间步长的选取受到限制的问题，文献[7]提出基于蛙跳的局部时间步长(local time-stepping，LTS)迭代格式，即不同的区域选取不同的时间步长，此时，各区域时间步长只受各自区域网格的影响，在时间步长的选取上有一定的限制，本文给出任意m∶n型LTS迭代格式，其中，m，n为任意正整数，可根据实际问题更加方便地选取不同时间迭代步长，并结合实际算例验证了该格式的正确性和有效性。

1 不连续伽辽金时域有限元法

1.1 DG-FETD基本原理

本文中采用四面体的网格离散目标模型。不连续伽辽金时域有限元法用于求解麦克斯韦方程时，必须保证磁场和电场在分界面上的切向连续性，因此，我们引入了连续性条件，已知的连续性条件有2种，中心通量(central flux)和迎风通量(upwind flux)[8]，本文需要通过中心通量来加强相邻元胞在公共面上的场量的连续性，其具体的公式推导过程为

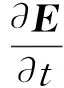
(1)

(2)

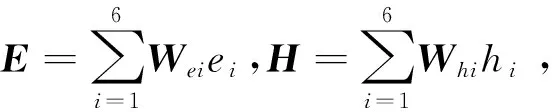
(3)—(4)式中：E+，H+表示相邻体在该面上电场和磁场；n表示元胞面的法向量。由(1)式和(2)式，采用伽辽金测试可得以下矩阵形式的半离散格式

(5)

(6)

(5)—(6)式中：

(7)

1.2 LTS迭代格式

对1.1节的半离散格式，在时间上采用蛙跳迭代格式为

(8)—(9)式中：Δt为选取的迭代时间步长；hn+1/2，hn-1/2分别表示n+1/2，n-1/2时刻的磁场强度；en,en-1表示n及n-1时刻的电场强度。

本文使用的是蛙跳的时间差分格式，与隐式差分格式相比，它的效果更好。因为其时间步长的选取可以通过CFL(Courant-Friedrichs-Lewy)条件计算出来，为了保证稳定性，必须使用最小剖分网格计算。针对多尺度问题中，DG-FETD稳定性受最小剖分尺寸影响导致整体时间步长的选取受到限制的问题，文献[9]提出基于蛙跳的局部时间步进(local time-stepping，LTS)迭代格式，即不同的区域选取不同的时间步长，此时，各区域时间步长只受各自区域的网格影响，提高了计算效率。它包含以下4个步骤。

步骤1计算最小时间步长，根据CFL条件，利用已知最小剖分网格的尺寸，计算出能满足整个区域稳定性条件所需的时间步长。

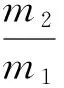
步骤3将所有网格分为2部分，根据步骤2的分组找出最佳的划分方法，达到最优的加速。在上述例子中，最优的划分方法是在第2组和第3组中间划分。

步骤4按照DG-FETD的方法对2个区域分别求解。

在LTS技术中最重要的一个部分就是对控制方程差分近似方法的改变。当整个求解区域选取Δt1，Δt22种大小的时间步长时，其中Δt1∶Δt2=m∶n，各自区域分别采用蛙跳迭代格式，此时，需要考虑2个区域分界面上的场值传递，下面以Δt=3Δt1=2Δt2为例介绍其迭代过程。

(10)

大部分实际应用问题都包含着更为复杂的结构，这时，固定比例的LTS技术效果就显得不够突出。我们通过改进，实现了任意比例的LTS技术，并将其应用在了DG-FETD中，取得了显著的效果。通过上面的描述，我们知道在LTS技术中，最重要的是时间上的近似，将需要用到的信息用已经存在的时间步内的信息近似，在每个时间上的衔接中加入嵌套循环，设1区域的未知量为e1和h1，2区域的未知量为e2和h2，若已知每个未知量n时刻的值，需求解n+1时刻的值，若Δt1∶Δt2=m2∶m1，即Δt=m1Δt1=m2Δt2，其中，Δt为实际的时间步长。1区域每个时间步应迭代m次，因电磁的未知量和磁场未知量分开计算，则1区域应计算2m1次，2区域应计算2m2次，具体实现步骤如图1所示。

通过引入LTS技术，在求解多尺度电磁问题时，DG-FETD能减少迭代所需的计算时间，更大地发挥优势，随着未知量的增加，这一优势会变得更加显著。

2 数值算例

为了验证本文提出的方法的正确性和有效性，算例1对半填充介质矩形金属谐振腔进行了分析，如图2所示。谐振腔尺寸是1 m×0.1 m×1 m，介质部分的相对介电常数是2，激励源是中心频率为300 MHz，带宽为400 MHz的调制高斯脉冲。计算区域中时间步长分别选取为Δt1=5.57 ps, Δt2=8.35 ps。

图3给出Δt=3Δt1=2Δt2与选取传统全局时间步长Δt1时的时域电场，结果吻合较好，表明所提出方法的正确性。

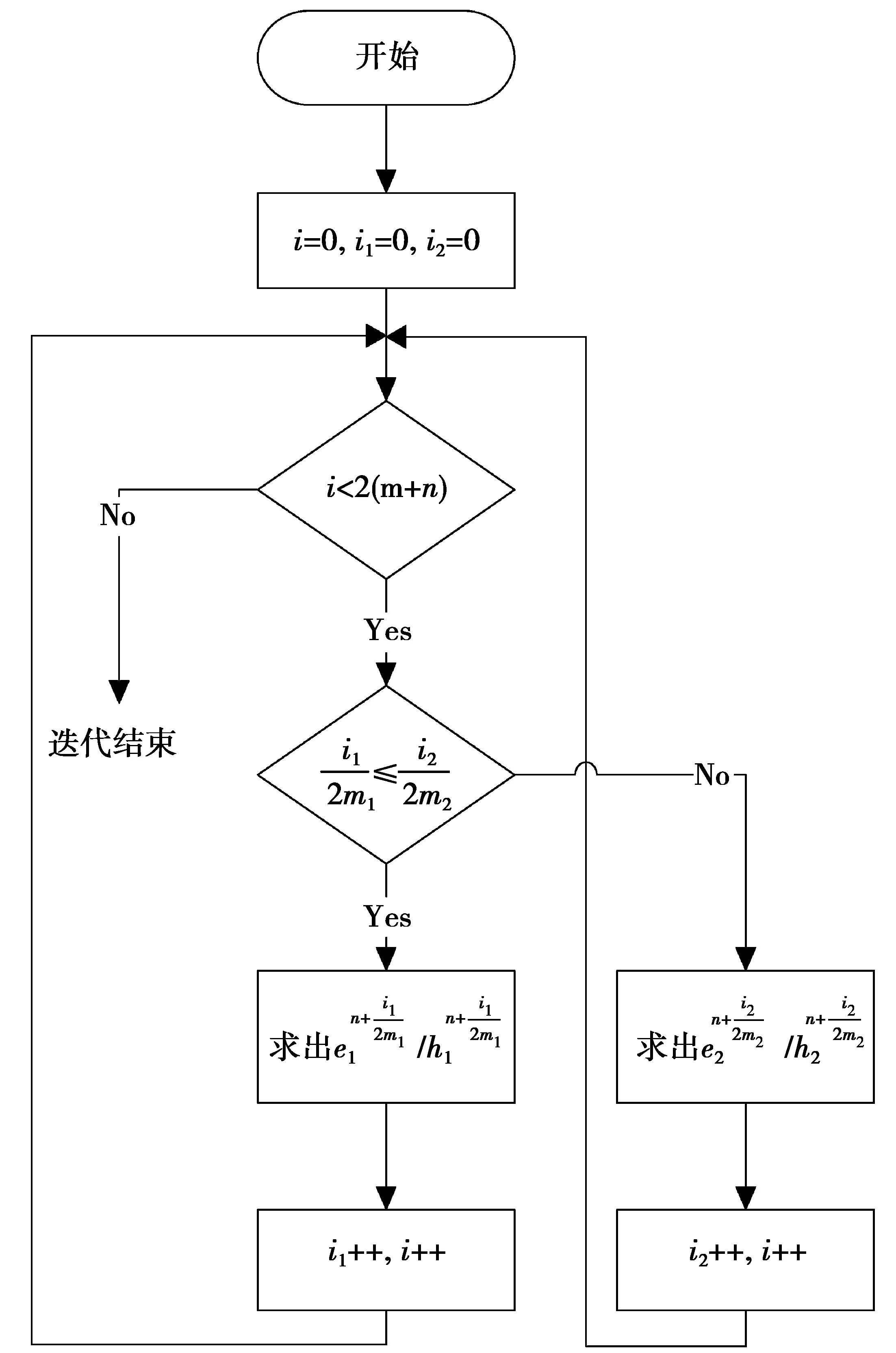
图1 LTS时间迭代流程图Fig.1 Flowchart for the time of iteration

图2 半填充介质谐振腔Fig.2 Half filled dielectric resonator

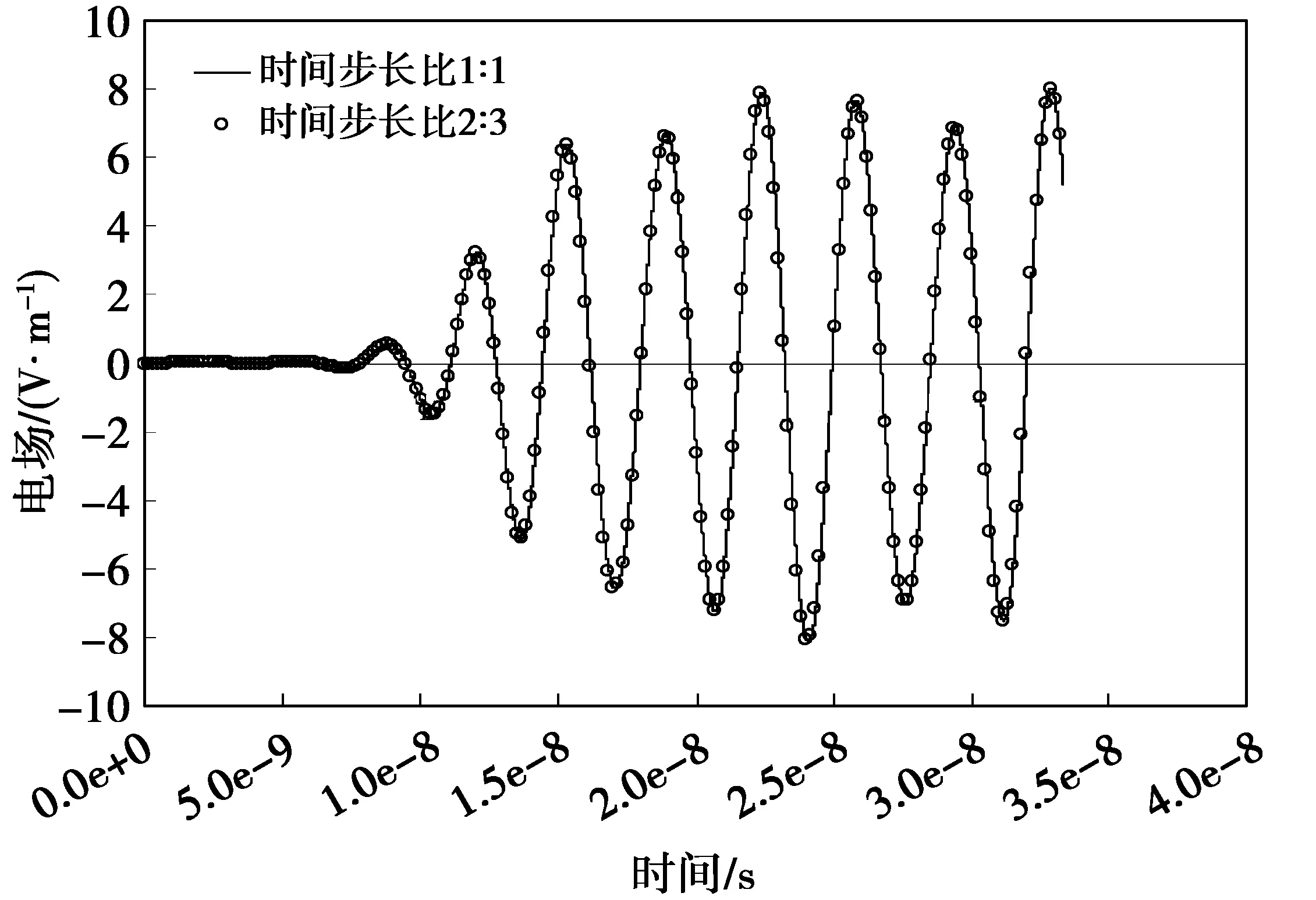
图3 时域电场比较Fig.3 Comparison of electric field in time domain

表1给出2种方法的计算时间比较，表明了所提出方法的有效性。

表1 计算时间比较Tab.1 Comparison of computation time

算例2是里面含有一个介质球的金属球，金属球半径为0.5 m，介质球半径为0.05 m，相对介电常数εr=9.0，在z=0 m处加入调制高斯脉冲，其中心频率为10 GHz，脉宽相关量为9，观察点为(0,0,0)。金属剖分尺寸为0.06 m，介质部分剖分尺寸为0.015 m，离散后得到22 989个四面体单元，未知量个数为267 260，分别用传统的DG-FETD和加入了LTS技术的DG-FETD计算该模型，其中，后者采用Δt1∶Δt2=1∶2.5的时间步长。

2种方法的时域电场波形如图4所示，吻合较好，可以证明此方法的正确性。本算例在四核8 GByte内存,主频为2 GHz，64位的台式机上运行，2种方法的计算资源对比如表2所示。在未知量个数相等的情况下，第2种方法在迭代时间上明显优于第1种方法，这也进一步证明了此方法的有效性。

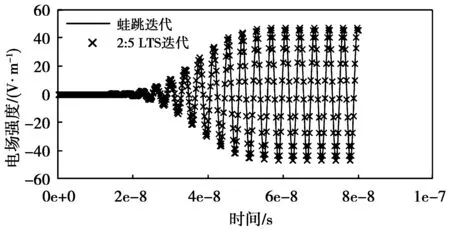
图4 LTS迭代与蛙跳迭代时域波形对比Fig.4 Comparison of time domain waveform between LTS and Leap-frog method表2 LTS迭代的DG-FETD与蛙跳迭代 DG-FETD计算资源对比Tab.2 Comparison of computation resource between iterative LTS method and iterative Leap-frog method for DG-FETD

迭代方法解析解/MHz谐振频率/MHz迭代步数迭代时间/s蛙跳迭代263.017262.460120001144LTS迭代(1∶2)263.017262.3176000645LTS迭代(2∶5)263.017262.2314800515

3 结 论

基于蛙跳的LTS技术的重点在于不同时间迭代步长区域交界面上的电磁场迭代处理方式，以便实现各区域时间步长只受各自区域的网格影响，并且保持各区域的显式迭代特性。本文在传统LTS技术的基础上通过引入任意比例LTS技术，提高了不同时间步长选取的灵活性，在求解多尺度电磁问题时，DG-FETD能减少迭代所需的计算时间，更大地发挥优势，随着未知量的增加，这一优势会变得更加显著，数值算例验证了该方法的正确性和有效性。

[1] JIN J M.The Finite Element Method in Electromagnetics[M].2nd ed. New York: Wiley, 2002.

[2] JIN J M，RILEY D J. Finite Element Analysis of Antennas and Arrays[J].Hoboken, NJ: Wiley, 2008: 56(8): 222-240

[3] HESTHAVENS J S, WARBURTON T.High-order Nodal methods on unstructured grids. I. Time-domain solution of Maxwell’s equations[J]. Comput Phys, 2002, 181(1): 186-221.

[4] COHEN G,FERRIE ′RES X,PERNET S.A spatial high order hexahedral Discontinuous Galerkin method to solve Maxwell’s equations in time domain[J].Comput Phys, 2006, 217(2): 340-363.

[5] REED W H, HILL T R.Triangular mesh methods for the neutron transport equation[M].Los Alamos: Los Alamos Scientific Laboratory Report LA-UR, 1973.

[6] CHEN J, LIU Q H.Discontinuous Galerkin Time-Domain Methods for Multiscale Electromagnetic Simulations: A Review[J]. Proceedings of the IEEE, 2013, 101(2):242-254.

[7] MONTSENY E, PERNET S, FERRIERES X,et al. Dissipative terms and local time-stepping improvements in a spatial high order discontinuous Galerkin scheme for the time-domain method for the time-domain Maxwell’s equations[J].Comput Phys，2008,227(14)：6795-6820.

[8] LI P, SHI Y, JIANG L J, et al. A Hybrid Time-Domain Discontinuous Galerkin-Boundary Integral Method for Electromagnetic Scattering Analysis[J].IEEE Transactions on Antennas & Propagation, 2014, 62(5):2841-2846.

[9] MONTSENY E, PERNET S, FERRIERES X, et al. Dissipative terms and local time-stepping improvements in a spatial high order discontinuous Galerkin scheme for the time-domain method for the time-domain Maxwell’s equations[J].Comput Phys，2008，227(14): 6795-6820.

[10] SCHOMANN S, GÖDEL N, WARBURTON T, et al.Local Timestepping Techniques Using Taylor Expansion for Modeling Electromagnetic Wave Propagation With Discontinuous Galerkin-FEM[J]. IEEE Transactions on Magnetics,2010, 46(8):3504-3507.

The Suqian Social Development Project Foundation(S201410)

ApplicationoflocaltimesteppingstrategywitharbitraryratioforthediscontinuousGalerkinFETDmethod

LI Min1,2, SHEN Weiwei2, YE Xiaodong3, YANG Yiting3

(1.School of Information Engineering, Suqian College, Suqian 223800, P.R.China； 2.College of Electronic and Optical Engineering, Nanjing University of Posts and Telecommunications, Nanjing 210033, P.R.China； 3.School of Electronic and Optical Engineering,Nanjing University of Science and Technology, Nanjing 210094, P.R.China)

The discontinuous Galerkin-finite element time domain(DG-FETD) method has the ability to deal with the multiscale problems. The size of time step is limited by the smallest spatial discretization of the simulation domain according to the stability condition when fine structures or high permittivity media occur. To handle this kind of problem, the local time-stepping technique with arbitrary ratio is proposed in the paper, which makes the selection of time step size more flexible and reduces the time of iteration. Numerical results demonstrate the correctness and efficiency of the proposed method.

discontinuous Galerkin; multi-scale; local time stepping

10.3979/j.issn.1673-825X.2017.06.005

2016-10-31

2017-06-01

沈微微 1105183311@qq.com

宿迁市社会发展(指令性)项目(S201410)

TN925

A

1673-825X(2017)06-0739-05

李 敏(1986 -)，女，山东济宁人，讲师，硕士，主要研究方向为时域电磁计算及其快速算法,超宽带辐射、散射理论与技术研究。E-mail:18800608557@163.com。

沈微微(1985 -)，女，江苏徐州人，硕士，研究方向为图形图像技术。E-mail: 1105183311@qq.com。

叶晓东(1967 -)，男，江苏南京人，副教授，主要研究方向为电磁场与微波技术，散射理论与技术研究。E-mail:yexiaodong@njust.edu.cn。

(编辑：王敏琦)