受分子寿命影响的中继最大可达传输速率

王嘉星，彭木根

(北京邮电大学 信息与通信工程学院，北京 100876)

受分子寿命影响的中继最大可达传输速率

王嘉星，彭木根

(北京邮电大学 信息与通信工程学院，北京 100876)

基于扩散的分子通信以分子作为信息载体进行信息的传输，分子在信道中做布朗运动，遵循菲克扩散定律。随着扩散距离的增加，分子浓度急速衰减，造成信道可达传输速率非常低，因此，可以采用中继传输来提高传输性能。鉴于扩散分子通信中继可达传输速率是业界研究的热点与难点，采用配体-受体结合机制，考虑分子寿命及分子到达概率等因素的影响，研究了基于扩散的分子通信中继信道对分子传输可达速率的影响，也探索了基于分子寿命的中继节点位置对中继可达传输速率的影响。仿真结果显示，随着分子寿命的增加，分子在信道中存在的时间增加，使得信道最大传输速率增大。同时，随着分子寿命的增加，中继节点需要靠向接收端，才能使信道最大传输速率达到最大。

分子通信；扩散；最大可达传输速率；分子寿命

0 引 言

分子通信是一种利用纳米设备进行信息传输的通信方式[1]。这些纳米设备具有计算、存储和驱动等功能，将这些纳米设备通过互联形成一个网络，称为纳米网络[2]。纳米设备在纳米网络间协同工作以克服各自的局限性。纳米机器之间通过信息分子的发射、传输和接收，达到信息交换的目的。这种想法受到自然界中细胞之间信息交换的启发。基于扩散的分子通信纳米网络技术具有广泛的应用前景，主要应用于生物医药及工业指示。分子通信中分子作为信息载体在流体介质中进行传输。由于分子做布朗运动，当接收端远离发射端时，分子的扩散将会发生严重的衰减，为此，分子通信的中继传输是一种重要的传输模式。

为了分析分子通信的传输性能，业界从信息论角度建立了基于扩散的分子通信传输模型以及相应的中继信道模型，且取得了初步进展。文献[3]分析了基于扩散的分子通信协作中继信道误码率性能，文献[4-9]利用不同的信道模型分析了基于扩散的分子通信信道容量，其中，文献[5]得到了关于分子通信信道容量的闭式表达式。文献[9-12]中介绍了有关于分子中继信道及多跳网络的研究。

目前有关扩散分子通信传输信息容量的研究还主要集中于特定的调制和编码方案，且不考虑分子扩散信道的记忆性及分子噪声特殊性的影响。文献[4]中考虑了码间干扰情况下，采用互信息最大化方法计算基于扩散的分子通信信道容量，但没有考虑信道中的噪声影响；而文献[13]中通过信道转移矩阵的方法计算基于扩散的分子通信信道容量，但没有考虑分子寿命的影响。为了克服已发表论文存在的问题，本文同时考虑码间干扰及信道噪声的因素，并且将分子寿命这一因素考虑在内，构建出普通二进制信道系统模型，并对其信道传输容量，即最大可达传输速率，进行分析推导。另外，中继节点的摆放位置对于中继信道最大可达传输速率有着重要影响。本文探求了增加中继节点后，中继对于扩散分子传输可达速率的影响以及基于分子寿命的中继节点位置对中继可达传输速率的影响。

1 系统模型

基于扩散的分子通信中继信道模型如图1所示。扩散分子通信与传统通信存在不同，信息的载体不再是电磁波，而是分子本身。这就使得分子通信的设备属于纳米级别，并且需要对分子类型进行相应的识别。同时，由于分子自由扩散，不需要额外的能量，因此，中继节点与接收端在进行信息解码时，不能按照传统的功率机制，而是需要对所接收到的分子数目或浓度进行阈值判断。本文建立的基于扩散的分子通信系统采用配体-受体结合机制，即接收端通过其表面上的化学接收器来识别信息分子。图1中，TN代表发射端；RN代表中继节点；RX代表接收端。中继节点与发射端、接收端位于同一直线上。发射端发射信息分子进入流体介质，分子做布朗运动在流体介质中自由扩散。同时，为了降低码间干扰的影响以及接收端的解码复杂度，中继节点采用异种分子解码转发方式进行信息传递。并且考虑到中继节点实际工作过程，假设其采用半双工方式进行通信。发射端与中继节点之间的距离为d12，中继节点与接收端之间的距离为d23。

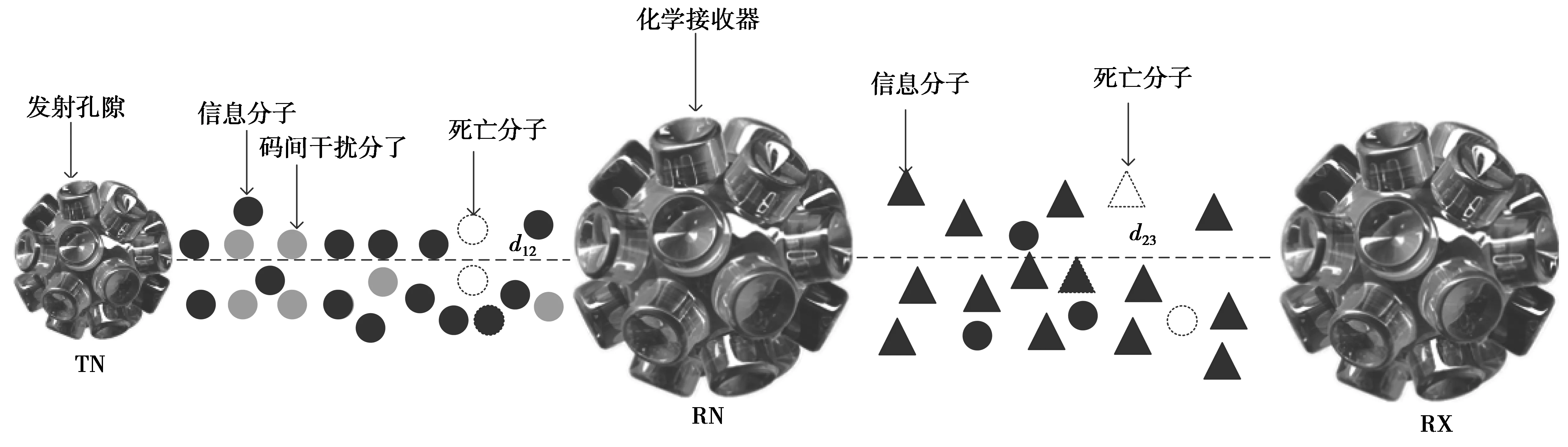
图1 基于扩散的分子通信中继信道模型Fig.1 Diffusion-based relay channel model for molecular communication

1.1 发射与接收过程

信号的发射和接收过程如图2所示。发射端通过发射孔隙将空间分为内外2个部分，允许信息分子自由出入。目前的研究分析并不依赖于精确的分子数目，而是通过信息分子的浓度变化来生成发射信号。发射端采用开关键控调节分子浓度发射二进制信号。接收过程通过接收端纳米机器上的化学接收器来实现。接收过程包括分子的捕获与释放。如果化学接收器上之前没有分子，则执行捕获反应；如果化学接收器上有分子，则执行释放反应。分子捕获速率为k+，释放速率为k-。每个时隙长度为T，在每一个时隙内只有一个符号信息被发送。

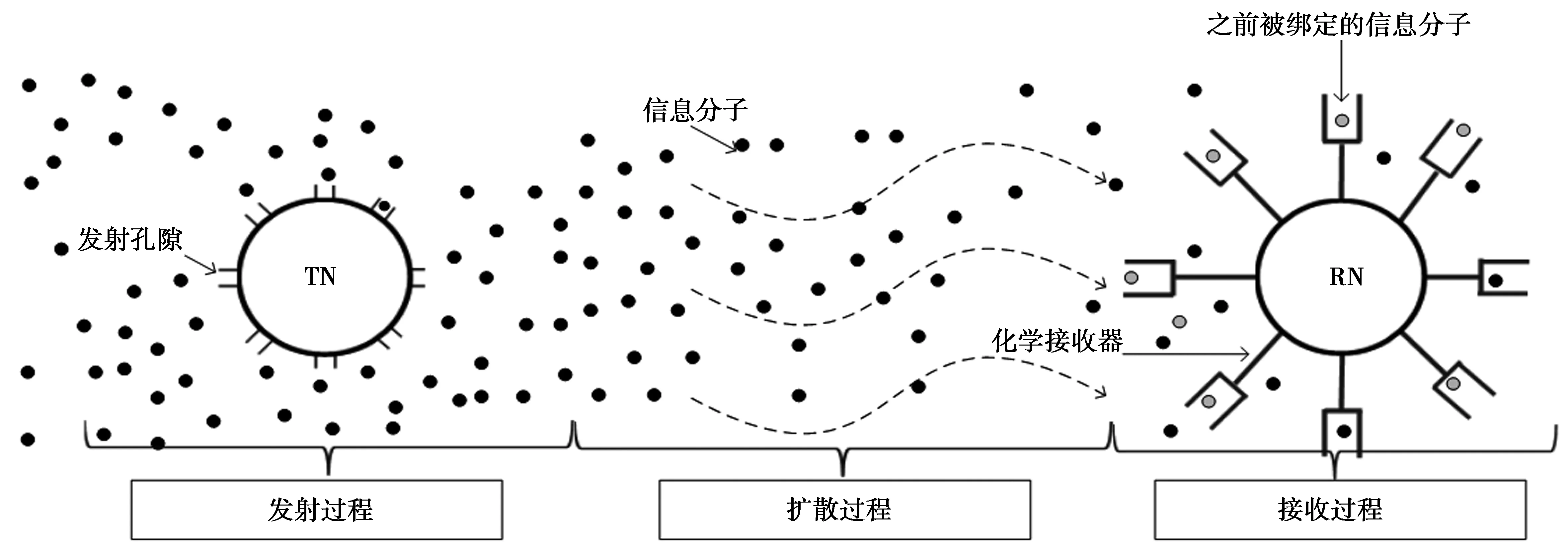
图2 分子的发射与接收过程Fig.2 Molecular emission and reception processes

1.2 基本传输过程

根据分子做布朗运动的扩散特性，考虑分子寿命和码间干扰的影响，则其满足Fick第一扩散定律

(1)

(1)式中：J表示扩散通量；D表示扩散系数；c表示分子浓度；d表示从发送端到接收端的距离；t表示扩散时间。

假设分子寿命服从指数分布，则

mn(u)=λe-λu

(2)

(2)式中，λ表示分子平均寿命的倒数。

如果分子的发射速率是常数Q，则分子浓度U(t,d)可以表示为

(3)

扩散浓度与距离的关系如图3所示。由图3可以看出，随着扩散距离的增加，分子浓度随之减小。在同一扩散距离处，时间越短，分子浓度越小，说明扩散是一个分子浓度累积的过程。

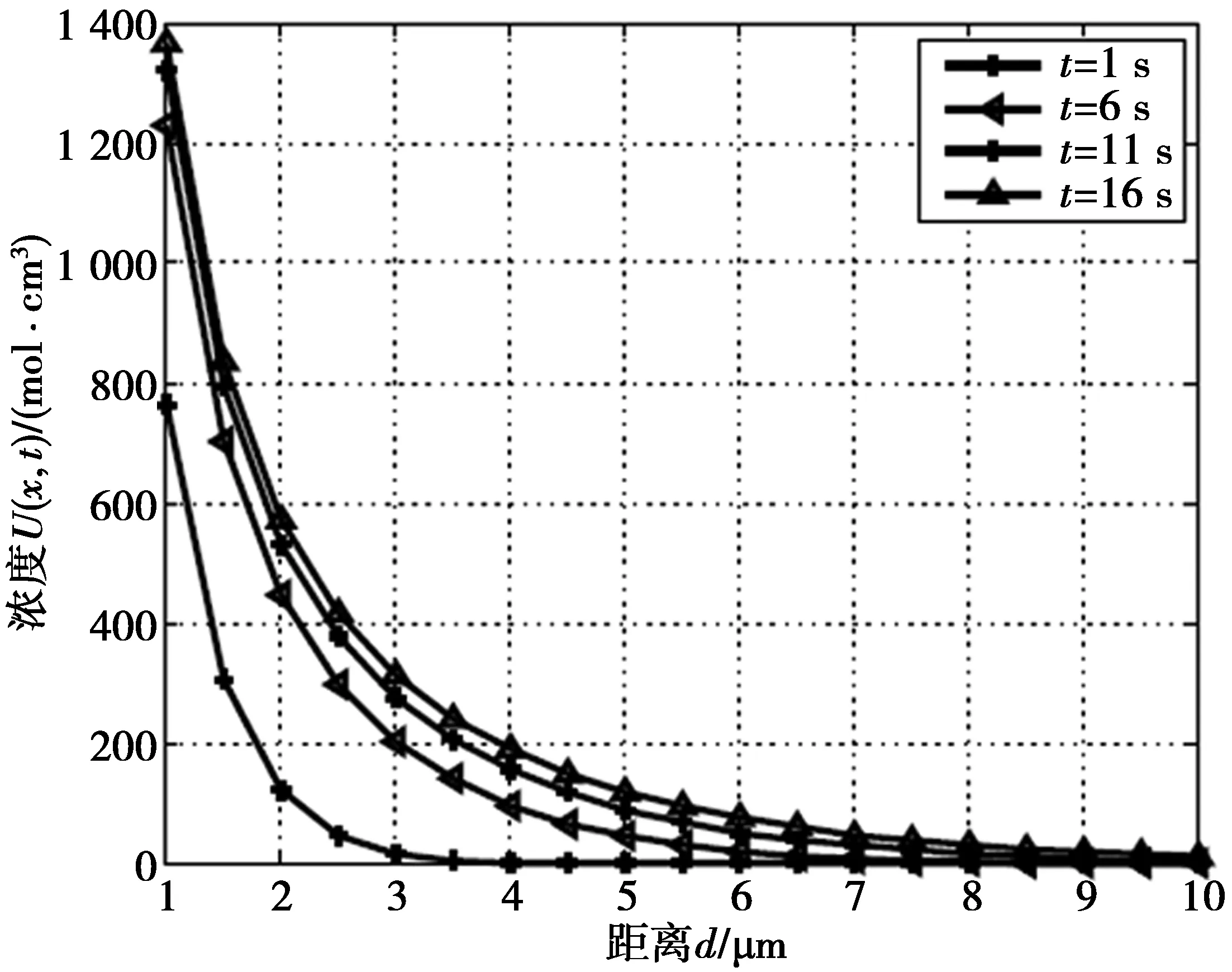
图3 浓度-距离关系图Fig.3 Relation between concentration and distance

由于分子扩散的堆积效应，使得信道中存在码间干扰。同时，由于分子布朗运动碰撞使得信道中存在分子热噪声n(t)。假设n(t)为加性高斯白噪声，均值为0。每个分子在时隙i发送，在时隙n到达的概率表示为

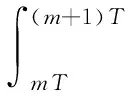
(4)

(4)式中，m=n-i。

(5)

2 中继信道最大传输速率

假设二进制信号发送的先验概率为p，当发送端分别发送二进制信号0和1时，接收端在第n个时隙检测到的概率分别为Pn和Qn，则

P[Yn=0|Xn=0]=Pn

(6)

P[Yn=1|Xn=1]=Qn

(7)

则错误概率分别为1-Pn和1-Qn。假设发送端和接收端有完美的时间同步机制。考虑码间干扰的影响，当时隙n≥2时，有

(8)

(9)

根据信息论基础，信道容量，即最大可达传输速率计算表示为

(10)

对于二进制离散信道，考虑时隙长度，信道最大可达传输速率(单位：bit/s)的计算表达式为

(11)

当n=1时，信道中不存在码间干扰，但存在噪声，因此假设

P1=p0，Q1=q0

(12)

互信息可以表示为

(13)

当n≥2时，互信息经推导可以表示为

(14)

中继节点前的信道最大可达传输速率(单位：bit/s)表示为

(15)

中继节点接收到的信息为

P(Y=0)=(1-p)Pn+p(1-Qn)

(16)

P(Y=1)=(1-p)(1-Pn)+pQn

(17)

经过中继节点之后，互信息可表示为

(18)

当时隙n≥2时，互信息推导所得为

(19)

中继节点后信道最大可达传输速率(单位：bit/s)表示为

(20)

最终信道最大可达传输速率可以表示为

C=min{C12,C23}

(21)

3 性能分析

3.1 参数设计

3.2 数值结果分析

中继节点对最大可达传输速率的影响如图4所示。从仿真结果上看，由下往上，每2条线作为一组进行对比。在没有中继节点的情况下，信道最大可达传输速率随着距离的增加逐渐减小，当在发射端与接收端中点位置(由于传输距离为80 μm，因此，中继节点位置在距离发送端40 μm处)加入中继节点之后，信道最大可达传输速率在中继节点加入的地方变大，也就是在相同传输距离的位置上，中继信道最大可达传输速率比直传信道的最大可达传输速率大，使得信道能够传输的信息量增加。

中继位置与信道最大可达传输速率的关系如图5所示。为了达到中继信道最大可达传输速率，随着分子寿命的增加，中继节点位置需要向接收端靠近。同时可以看出，最大可达传输速率随着分子寿命的增加而增大，这是因为在发射速率不变的情况下，信息分子在信道中的存活时间增加，使得信道传输容量增大。当分子寿命λ<0.4时，中继节点位置需要靠近发送端。中继节点的位置直接影响发射端到中继节点以及中继节点到接收端的距离。最终的信道最大可达传输速率取决于两跳中最大可达传输速率中较小的那一个。为了达到优良的性能，中继节点应当放在两跳信道最大可达传输速率相差不大的位置上。

图4 中继节点对可达传输速率的影响Fig.4 Influence of relay nodes on the achievable transmission rate

图5 中继位置与信道最大可达传输速率的关系Fig.5 Relation between the relay location and the channel maximum achievable transmission rate

4 结束语

本文介绍了基于分子扩散的非协作中继信道传输系统模型，研究了中继传输对扩散分子传输可达速率的影响，同时探求了在考虑分子寿命这一影响因素下的中继节点位置对中继可达传输速率的影响。中继节点采用异种分子解码转发进行信息传递，降低了码间干扰及接收端的解码复杂度。通过仿真可以看出，增加中继节点之后，相同传输距离上的信道最大传输速率比直传信道最大传输速率增大。而且，随着分子寿命的增加，中继节点的位置需要向接收端靠近才能使得信道传输速率达到最大。

[1] FARSAD N， YILMAZ H B，ECKFORD A， et al. A comprehensive survey of recent advancements in molecular communication[J]. IEEE Communications Surveys & Tutorials，2016，18(3)：1887-1919.

[2] AKYILDIZ F，PIEROBON M，BALASUBRAMANIAM S， et al. The internet of Bio-Nano things[J].IEEE Communications Magazine，2015 ，53(3)：32-40.

[3] WANG X， HIGGINS M D， LEESON M S，et al. Relay analysis in molecular communications with time-dependent concentration[J].IEEE Communications Letters，2015，19(11)：1977-1980.

[4] LIU Qiang，YANG Kun，HE Peng，et al. Channel capacity analysis for molecular communication with continuous molecule emission[C]//IEEE.Wireless Communication and Signal Processing(WCSP).Hangzhou，China ：IEEE Press，2013：1-6.

[5] PIEROBON M， AKYILDIZ I F. Capacity of a diffusion-based molecular communication system with channel memory and molecular noise[J].IEEE Transactions on Information Theory， 2013，59(2)：942-954.

[6] NAKANO T，OKAIE Y， LIU J Q. Channel model and capacity analysis of molecular communication with brownian motion[J].IEEE Communications Letters，2012，16(6)：797-800.

[7] EINOLGHOZATI A, SARDARI M, FEKRI F.Capacity of diffusion-based molecular communication with ligand receptors[C]//IEEE.IEEE Information Theory Workshop(ITW). New York：IEEE Press，2011：85-89.

[8] FARSAD N, MURIN Y, ECKFORD A，et al. Capacity limits of diffusion-based molecular timing channels[EB/OL].(2017-02-25)[2017-04-02].http://xueshu.baidu.com/s?wd=paperuri%3A%280cdf218824aa89912482e4c88ad46b94%29&filter=sc_long_sign&tn=SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Farxiv.org%2Fabs%2F1602.07757&ie=utf-8&sc_us=16879249461316764517.

[9] SINGHAL A, MALLIK R K, LALL B. Performance Analysis of Amplitude Modulation Schemes for Diffusion-Based Molecular Communication[J].IEEE Transaction on Wireless Communications，2015，14(10)：5681-5691.

[10] WANG X, HIGGINS M D, LEESON M S. Distance estimation schemes for diffusion based molecular communication systems[J].IEEE Communications Letters, 2015，19(3)：399-402.

[11] AHMADZADEH A, NOEL A, SCHOBER R. Analysis and design of two-hop diffusion-based molecular communication networks[C]//IEEE GLOBECOM. New York：IEEE Press，2014：2820-2825.

[12] NAKANO T，LIU J Q. Design and analysis of molecular relay channels: an Information theoretic approach[J].IEEE Transaction on Nanobioscience， 2010，9(3)：213-221.

[13] ATAKAN B，AKAN O B. On channel capacity and error compensation in molecular communication[J].Transactions on Computational Systems Biology X ，2008(5410)：59-80.

[14] ATAKAN B，AKAN O B. Single and multiple-access channel capacity in molecular nanonetworks[C]// International ICST Conference, Nano-Net 2009.Lucerne, Switzerland：Springer Berlin Heidelberg Press，2009:14-23.

s：The State Major Science and Technology Special Projects(2016ZX03001020-006); The National Natural Science Foundation of China (61361166005, 61671074); The Science and Technology Development Project of Beijing Municipal Education Commission of China(KZ201511232036); The National Program for Support of Top-notch Young Professionals

Relaymaximumachievabletransmissionrateaffectedbymolecularlifetime

WANG Jiaxing, PENG Mugen

School of Information and Communication Engineering, Beijing University of Posts and Telecommunications, Beijing 100876, P.R.China)

Diffusion-based molecular communication makes molecules as the information carrier for the information transmission, the molecules do Brownian motion in the channel, following the Fick’s law. With the diffusion distance increasing, the molecular concentration is rapidly attenuated, resulting in a very low channel achievable transmission rate. Therefore, relay can be used to improve the transmission performance. In view of the transmission rate in diffusion-based molecular communication relay channel is a hot spot in the field of research, this paper adopts the ligand-receptor binding mechanism, considering the molecular lifetime, molecular reach probability and other impact factors, and study the influence of achievable transmission rate in diffusion- based molecular communication, the paper study also investigates the effect of relay achievable transmission rate in the relay node location based on molecular lifetime. The simulation results show that with the molecular lifetime increasing, the time of the molecules in the channel increases, and the maximum transmission rate increases. At the same time, with the molecular lifetime increasing, the relay node need to approach to the receiver node so as reach the maximum transmission rate.

molecular communication; diffusion; maximum achievable transmission rate; molecular lifetime

10.3979/j.issn.1673-825X.2017.06.003

2017-04-21

2017-09-09

彭木根 pmg@bupt.edu.cn

国家重大科技专项(2016ZX03001020-006)；国家自然科学基金(61361166005，61671074)；北京市教育委员会科技发展项目(KZ201511232036)；全国杰出青年专业人才培养计划

TN929.53

A

1673-825X(2017)06-0726-06

王嘉星(1988 -)，女，河北石家庄人，博士研究生，主要研究方向为分子通信。E-mail:jx19882008@163.com。

彭木根(1978 -)，男，江西吉安人，教授，博士生导师，主要研究方向为无线通信理论，信号处理及协作通信等。E-mail:pmg@bupt.edu.cn。

(编辑：王敏琦)