基于改进克里金插值的室内定位位置指纹库构建方法

刘辉元，马金辉，黄 琼

(1.重庆市工业学校 网络信息中心，重庆 400043；2.重庆邮电大学 移动通信技术重点实验室，重庆 400065)

基于改进克里金插值的室内定位位置指纹库构建方法

刘辉元1,2，马金辉2*，黄 琼2

(1.重庆市工业学校 网络信息中心，重庆 400043；2.重庆邮电大学 移动通信技术重点实验室，重庆 400065)

当今社会对基于位置服务尤其是室内位置服务的需求日益迫切。位置指纹法利用室内无线信号强度来进行定位，具有方便快捷、低成本等优势，但构建一个细粒度的位置指纹库需要耗费大量的人力和时间。为提高位置指纹库的构建效率，提出一种基于改进克里金插值的位置指纹库构建方法。通过部分测量数据结合克里金插值法进行插值，并利用模拟退火算法提高理论变异函数拟合精度，进而估计出未测量点处的信号强度，提高插值精度和指纹库的构建效率。实验表明：相比反距离加权插值和传统克里金插值，该方法不但具有较高插值和定位精度，而且可将指纹数据人工采集工作量降低50%。

室内定位；位置指纹；克里金插值；模拟退火算法

0 引 言

近几年来，随着智能终端和通信技术的快速发展，基于位置服务[1]已成为日常生活不可或缺的重要元素。滴滴打车、摩拜共享单车等创新性服务都与定位技术的发展和应用息息相关。但由于室内空间的复杂性和特殊性，受部署难度、功耗、定位效率及精度的限制，室内定位技术还并不完善。

当前室内定位系统采用的相关算法主要分为基于测距和非测距两大类[2]。由于无线信号在复杂的室内环境中多径传播严重，具有较强的时变性，以及测量设备参考时钟的不精确性等，导致基于测距的方法在室内定位中存在实施成本较高，误差较大，稳定性较差。非测距类的主要为基于接收信号强度指示(received signal strength indication，RSSI)的位置指纹定位[3]，具有检测设备成本低，测量信号稳定性好，定位方法简单等优势。位置指纹定位法可分为2个阶段[4]，即离线构建位置指纹库阶段和在线匹配定位阶段。离线采集位置指纹来构建指纹库，一般通过人工测量来实现。而指纹库构建的准确性直接关系到在线阶段定位的精度，所以往往要尽可能布置大量参考点，每个参考点要进行多次测量来保证数据的准确性。当定位区域面积过大时，构建指纹库所耗费时间和人力将无法承受。

为解决这一问题，文献[5]提出采用矩阵填充的方法构建位置指纹库；文献[6]提出使用径向基函数插值法对指纹数据库进行插值；文献[7]使用重心拉格朗日插值计算参考点的信号强度；文献[8]提出根据信号传播模型估算未知点的指纹数据；文献[9]则采用克里金插值(Kriging interpolation)的方法构建指纹库。插值法可以减少人工采集工作量，考虑到室内无线信号强度的空间相关性，克里金插值通过变异理论考虑了整体空间对待测点的影响[10]，有更高的插值准确度。但传统克里金对理论变异函数的拟合往往采用经验法或最小二乘法，拟合度较低直接影响到插值精度。

因此，本文研究由模拟退火法(simulate anneal arithmetic，SAA)改进的克里金插值来进行位置指纹库插值构建，在传统克里金插值的基础上引入模拟退火法，提高变异函数模型的精度，进而通过对采集的位置指纹进行插值来构建细粒度、高精度的指纹库，以此降低离线阶段人工采集指纹数据的工作量。

1 位置指纹定位法

本文所使用的位置指纹定位系统由低功耗蓝牙 (bluetooth low energy，BLE)无线接入设备(access point，AP)、移动终端和服务器构成。利用位置指纹法[11]进行室内定位，需要先采集位置指纹数据存入数据库。定位时通过特定算法将待定位点的信号强度数据与位置指纹库中的指纹数据进行逐一匹配，从中找出最为相似的位置指纹获取定位结果。位置指纹定位法包括离线阶段和在线阶段，其工作原理示意图如图1所示。

图1 位置指纹定位工作原理示意图Fig.1 Schematic diagram of location fingerprint working principle

2 反距离加权插值法

反距离加权插值法在各个领域获得了广泛应用。其插值原理是利用空间的相近相似，即距离越近相似度越高，插值点与周围已知点的远近决定权重的大小，再取加权平均结果作为插值结果，其计算方法为

(1)

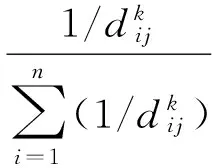
(2)

(3)

(1)-(3)式中：Zj为待插值点的特征值；Zi为周围已知点的特征值；m为周围已知点的数量；wij为周围点对待插值点的权重；dij为周围第i个已知点与第j个插值点间的距离；k为反比幂指数，反比幂指数k决定着权重值随距离改变的速率大小，实际使用时通常取为2。

反距离加权插值法拥有算法原理简单，易于实现，当数据量丰富和空间特征连续性较好时插值效果比较理想等优势。然而其加权平均处理的方法，仍会削弱区域内观测属性分布特征，难以进行精确的插值。

3 克里金插值法

克里金插值法，又被称作空间数据插值法[12]。该方法根据区域化变量和变异函数理论，探究随机性和空间相关性并存的空间数据，并进行最优无偏估计。与反距离加权插值法类似，克里金插值法同样采用加权平均的方式进行插值，计算公式为

(4)

(4)式中：Z*(x0)为插值点x0处的估计值；Z(xi)为n个已知点中xi处的测量值；λi为对应的权重。

与反距离加权插值不同，克里金插值法的权重系数λi不仅关注未知点和已知点2点间的远近关系，还通过变异理论从整体信号空间变异结构的角度来考量已知点间的关系及其对插值位置的影响，使插值结果更准确更符合真实环境。

3.1 区域化变量

区域化变量可理解为一个与在区域中所处位置有关的随机变量，本文中指定位区域内不同位置上的蓝牙BLE信号强度。在实验区域范围内点x和点x+h处的特征值Z(x)和Z(x+h)存在着一定的自相关性，其关联程度与距离向量h有关。

3.2 变异函数

变异函数反映了区域化变量的空间结构性变化和随机性变化[13]。区域化变量Z(x)的变异函数γ(h)可以描述Z(x)与Z(x+h)变异水平，理论变异函数的计算公式为

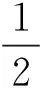
(5)

理论变异函数的计算需要通过尽可能多的测量数据来获得区域化变量的期望，但现实中进行室内定位时不可能对蓝牙BLE信号强度进行无限多次测量。因此，只能根据已测得的信号强度样本数据来估计出变异函数值，而这样得到的离散变异函数被称为实验变异函数，可按照(6)式来进行计算。

(6)

(6)式中，N(h)代表分离距离为h时的点对数目。实验变异函数以离散的形式给出了信号强度在当前各采样间距下的空间变异结构，但还需求出描述信号强度在任意间距下空间变异结构的理论变异函数。该过程可通过选取理论变异函数模型与现有实验变异函数拟合完成。传统克里金方法在确定理论变异函数模型中的参数时往往采用经验法或最小二乘拟合来实现，经验法仅能获得粗略信息，而最小二乘容易陷入局部最优解导致拟合精度较低。本文引入模拟退火算法提高变异函数模型的拟合精度，使模型能更准确地描述室内环境中蓝牙BLE信号强度的变异特征，进而提高模型的插值准确度。

3.3 插值点估计

由 (4) 式可知，要想求得Z(x0)的信号强度，关键就是要计算出权重λi的值。它的取值并非仅仅取决于2点之间的距离，而是通过变异函数在无偏性和最小方差条件下计算得到。在此条件下，可以推出普通克里金方程组为

(7)

待估系数λi的求解方程可用矩阵的形式可以表达为

(8)

(8)式中，变异函数值γ(xi-xj)可以通过拟合得到的理论变异函数来获得，求解矩阵方程得到权重系数λi(1≤i≤n)，代入(1)式得到估计值Z*(x0)，即为待估位置x0处蓝牙BLE信号强度的插值结果。

4 基于改进克里金插值的位置指纹库构建方法

为降低构建位置指纹库的工作量，首先在定位区域部分参考位置测量蓝牙BLE信号强度，根据(6)式计算出实验变异函数。本文引入较为成熟的模拟退火的方法来拟合得到理论变异函数，依(8)式计算出权重系数λi，进而可按照(4)式估计出待估位置处的信号强度值。下面介绍模拟退火法拟合理论变异函数的方法。

4.1 模拟退火法拟合理论变异函数

模拟退火法模拟了热力学中固体退火过程[14]，温度充分高的固体在缓慢降温的过程中，粒子排列渐趋有序，内能不断减小，最后达到基态。对给定的理论变异函数模型参数任意初始状态(C0,C,a)，利用扰动方法产生新的状态，根据状态接受函数确定是否接受该状态。通过不断迭代，温度缓慢降低，该算法可以有效地跳出局部极小解而最终趋于全局最优，同时可以避免复杂的求导运算和大型矩阵方程组求解，程序实现简单。

4.1.1 变异函数模型

对于克里金插值的理论变异函数模型，本文选取应用最为广泛的球状模型，具体形式为

(9)

(9)式中：C0为块金值；C为偏基台值；a为变程。

4.1.2 目标函数

随着样本点对之间的距离h的不断增大，其空间相关性减弱变异性增强，同时参加计算的样本点对数目逐渐减少会使样本反映的统计特性偏离实际，进而导致可靠性降低。因此，在所得的实验变异函数中，靠近原点处的点比远离原点处的点更为可靠。在拟合理论变异函数时，不同分离距离下的点应区别对待，对可靠性较高的点予以更高的权重，同时降低可靠性较低的点对模型参数确定时的影响。因此，本文在使用模拟退火算法对理论变异函数进行拟合时，采用的目标函数为

(10)

(10)式中：γ*为实验变异函数；n为分离距离的个数；hi为第i个分离距离。

4.1.3 新状态产生函数

模拟退火算法中通过对当前模型参数m=(C0,C,a)进行扰动得到新状态m′，这个扰动是由随机函数来控制的。本文的模型扰动是根据依赖于温度的似Cauchy分布[15]产生新模型，具体形式为

(11)

yi=Tsgn(μ-0.5)[(1+1/T)|2μ-1|-1]

(12)

4.1.4 状态接受函数

状态接受函数是算法免于陷入局部极值的关键。状态接受函数根据Metropolis准则[16]，当扰动后所得新状态的目标函数值较原状态低时，以概率1接受新状态下的模型参数；否则，以一定概率P接受新状态，可在[0,1]产生一个服从均匀分布的随机数μ，若P>μ则接受新状态，否则舍弃。状态接受函数为

(13)

(13)式中：E0为扰动前原状态的目标函数值；E1为扰动后新状态的目标函数值；q为常数。

4.1.5 退温函数

模拟退火法模拟高温物体，从较高的初始温度开始逐渐缓慢降温，退温函数为

T(k)=T0αk1/N

(14)

(14)式中：T(k)为第k次迭代时的温度；T0为初始温度；α,N为给定常数；k为迭代次数。

4.2 算法描述

使用模拟退火算法拟合理论变异函数的流程图如图2所示。

图2 模拟退火算法拟合理论变异函数流程图Fig.2 Flow chart of simulated annealing algorithm fitting the theoretical variogram

图2中，模拟退火算法拟合理论变异函数的具体步骤如下。

Step1初始化，随机设定变异函数模型参数m=(C0,C,a)，模拟退火算法具有鲁棒性，最终解不依赖于初始解的选取，可从任意初始解开始。

Step2根据(10)式计算目标函数值E0=E(C0,C,a)。

Step5计算ΔE=E1-E0。

Step6按照状态接受函数(13)式进行判断，若ΔE<0，则新模型参数m′被接受；若ΔE≥0，计算概率P=[1-(1-q)ΔE/T]1/(1-q)并取q=-5，产生一个随机数μ～U[0,1]，当P>μ时接受新模型参数m′，否则舍弃。

Step7当模型参数被接收时，置m=m′。

Step8在温度T下，将Step 3—Step 7的扰动和接收过程重复进行50次。

Step9根据(14)式缓慢降低温度，取T0=103，α=0.95，N=1。

Step10重复Step 3—step 9，直到满足收敛条件，即目标函数值E<0.01，或温度T(k)<ε，ε为某个大于0的小数，输出理论变异函数模型参数最优值。

5 结果与分析

5.1 实验条件

为了评估所提指纹库构建方法的性能，本文选取宽12 m,长20 m的典型室内环境进行实验，实验区域示意图如图3所示。在该区域内设置5个蓝牙BLE基站AP1～AP5，分别位于区域的中心和4个角落。其中，AP1～AP4固定在墙壁距离地面2.5 m位置处，AP5固定在距离地面3.5 m的天花板上。移动终端设备采用基于安卓系统的小米4(电信4G版)手机来检测、收集、存储蓝牙BLE信号强度数据。

将实验场地划分为240个边长为l m的正方形网格，取各个网格的中心点作为采样位置点，对蓝牙BLE信号强度进行逐点实测采集。每个采样点依次对AP1～AP5进行100次采样取均值，得到各点的RSSI指纹向量：

Ri=(Ri1,Ri2,Ri3,Ri4,Ri5),

i=1,2,…,240

(15)

(15)式中：Ri为第i个采样点的指纹向量；Ri1～Ri5为第i个采样点接收到的各个AP的信号强度。将所得240个参考样本点的指纹向量作为实验样本数据集。下面从插值精度和定位结果2个方面来验证基于改进的克里金插值法构建位置指纹库的精度和有效性。

图3 实验场景示意图Fig.3 Schematic diagram of experimental scene

5.2 插值精度分析

在实验样本数据集中进行随机抽取，分别取40，80，120，160，200个样本指纹数据作为已知点指纹集，对其余200，160，120，80，40个未知位置点分别通过本文所提算法、使用最小二乘拟合的传统克里金插值法和反距离加权插值法进行插值估计，并将估计误差定义为

(16)

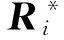
图4 3种算法的插值估计误差比较Fig.4 Comparison of three algorithms for interpolation estimation error

图4表明，在不同已知指纹数量下，本文方法的插值估计误差均小于传统克里金和反距离加权插值法，性能较传统克里金法有10%左右的提高。当已知指纹数量为120达到实验样本指纹总量一半时，即可使估计误差降至5%左右，并且随着已知指纹数量的增多估计误差稳步降低。本文方法充分考虑了信号空间变异结构对待测点的影响，已知指纹数量越多对室内无线信号环境的刻画越准确。

考虑到参考指纹位置分布对估计误差的影响，在实验区域内采用均匀抽取参考指纹点的方式进行克里金插值估计，结果如图5所示。

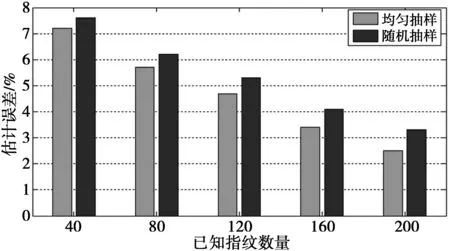
图5 均匀与随机抽样下克里金插值估计误差对比Fig.5 Kriging interpolation estimation error comparison of uniform and random sampling

图5表明，当参考指纹均匀分布于实验区域内时，本文方法插值估计误差进一步降低。这是因为此时参考样本可以更加充分地反映出室内环境中RSSI的空间变异结构，所得到的理论变异函数更加符合实际，对待测点的信号强度估计就更加准确。

5.3 定位结果分析

分别在实验区域内均匀抽取40，80，120，160，200个参考指纹点，采用上述3种插值方法构建出不同的完整指纹库，并将其与全部240个实验样本集所构成的位置指纹库作对比。在线阶段模式匹配采用K最近邻(K-nearest neighbor,KNN)算法来进行定位，其中K取为4。在实验区域内随机选取50个测试点进行定位，重复实验并统计定位平均误差，结果如图6所示。

图6 定位结果平均误差对比Fig.6 Mean error comparison of positioning results

由图6可知，较传统克里金和反距离加权插值法，采用本文方法构建位置指纹库时，在线阶段定位平均误差明显较低。仅需120个参考指纹，按照本文方法所构建的位置指纹库定位精度已经与逐点采样十分接近。因此，采用本文的位置指纹库构建方法可使离线阶段人工采集信号强度的工作量降低50%。

考虑到不同的模式匹配算法对定位误差的影响，再采用加权KNN(weighted KNN,WKNN)算法进行匹配定位。用120条指纹通过本文方法进行插值构建位置指纹库，并与240条指纹的全采样指纹库进行对比，并统计2 m和3 m内的误差累计概率，结果如表1所示。

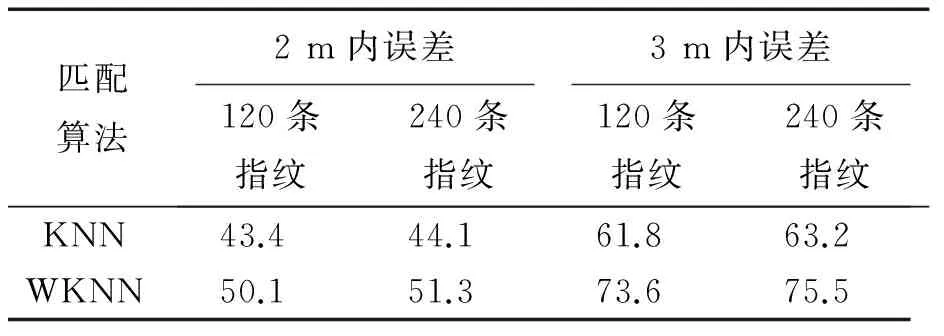
表1 KNN和WKNN的误差累计概率对比Tab.1 Error cumulative probability comparison between KNN and WKNN %

表1表明，采用不同的模式匹配算法时，本文方法依然只需约一半的参考指纹数量即可达到逐点采样的定位精度。而且，随着模式匹配算法性能的提高，采用本文方法所构建指纹库的定位精度也不断提高。

6 结束语

本文针对位置指纹室内定位技术中离线阶段位置指纹库构建工作量的问题，提出了一种基于改进克里金插值的指纹库构建方法。在定位区域部分，参考位置采集信号强度数据，结合克里金插值法进行插值，并采用模拟退火算法对实验变异函数进行拟合获取理论变异函数，提升离线阶段未测量点的信号强度插值精度，大幅降低指纹库构建所需的指纹采集数量。最后实验表明，所提方法在插值精度和定位精度方面均优于反距离插值和传统克里金插值，在保证定位精度的情况下可将位置指纹库构建工作量降低50%。

[1] 唐科萍,许方恒,沈才樑.基于位置服务的研究综述[J].计算机应用研究, 2012, 29(12):4432-4436.

TANG Keping, XU Fangheng, SHEN Cailiang. Survey on location-based services[J]. Application Research of Computers, 2012, 29(12):4432-4436.

[2] DALCE R, VAL T, BOSSCHE A V D. Comparison of Indoor Localization Systems Based on Wireless Communications[J]. Wireless Engineering and Technology, 2011, 2(4):240-256.

[3] KAEMARUNGSI K, KRISHNAMURTHY P. Analysis of WLAN’s received signal strength indication for indoor location fingerprinting[J]. Pervasive & Mobile Computing, 2012, 8(2):292-316.

[4] FARAGHER R, HARLE R. Location Fingerprinting With Bluetooth Low Energy Beacons[J]. IEEE Journal on Selected Areas in Communications, 2015, 33(11):2418-2428.

[5] 李文浩,李丽娜,徐攀峰,等.基于矩阵填充的室内定位位置指纹库构建[J].辽宁大学学报(自然科学版), 2015(4):325-329.

LI Wenhao, LI Lina, XU Panfeng, et al. Construction of Indoor Location Fingerprint Database Based on Matrix Completion[J]. Journal of Liaoning University, 2015(4):325-329.

[6] 夏英,王磊,刘兆宏.基于无线局域网接收信号强度分析的混合室内定位方法[J].重庆邮电大学学报：自然科学版, 2012, 24(2):217-221.

XIA Ying,WANG Lei,LIU Zhaohong.Hybrid indoor positioning method based on WLAN RSS analysis[J].Journal of Chongqing University of Posts and Telecommunications：Natural Science Edition,2012,24(2):217-221.

[7] 毛勤,曾碧,叶林锋.改进的室内移动机器人模糊位置指纹定位研究[J].计算机科学,2015,42(11):170-173.

MAO Qin, ZENG Bi, YE Linfeng. Research on improved indoor mobile robot fuzzy position fingerprint localization[J]. Computer Science, 2015, 42(11): 170-173.

[8] LI J, ZHANG B, LIU H, et al. An Indoor Hybrid Localization Approach Based on Signal Propagation Model and Fingerprinting[J]. International Journal of Smart Home, 2013, 7(6):157-170.

[10] 李方,王铁成,佟为明.基于空间变异理论的电子地图构建方法[J].哈尔滨工程大学学报, 2012, 33(6):715-719.

LI Fang, WANG Tiecheng, TONG Weiming. A method for radio-map construction based on the spatial variability theory[J].Journal of Harbin Engineering University,2012, 33(6):715-719.

[11] SWANGMUANG N,KRISHNAMURTHY P.An effective location fingerprint model for wireless indoor localization[J].Pervasive & Mobile Computing,2008,4(6):836-850.

[12] MANIRABONA A, FOURATI L C. A Kriged Fingerprinting for Wireless Body Area Network Indoor Localization[J]. Wireless Personal Communications, 2015, 80(4):1501-1515.

[13] LIU X, SHANNON J, VOUN H, et al. Spatial and temporal analysis on the distribution of active radio-frequency identification (RFID) tracking accuracy with the Kriging method[J]. Sensors, 2013, 14(11): 20451-20467.

[14] MEYSAMMOUSAVI S, TAVAKKOLI-MOGHADDAM R. A hybrid simulated annealing algorithm for location and routing scheduling problems with cross-docking in the supply chain[J]. Journal of Manufacturing Systems, 2013, 32(2): 335-347.

[15] SUN L X, XIE Y L, SONG X H, et al. Cluster analysis by simulated annealing[J]. Journal of Chemometrics, 2015, 10(4): 325-342.

[16] GENG X, CHEN Z, YANG W, et al. Solving the traveling salesman problem based on an adaptive simulated annealing algorithm with greedy search[J]. Applied Soft Computing, 2011, 11(4): 3680-3689.

The Key Industry Common Key Technology Innovation of Chongqing Municipal Science and Technology Commission (cstc2015zdcy-ztzx40008)

ConstructionmethodoffingerprintdatabasebasedonimprovedKriginginterpolationforindoorlocation

LIU Huiyuan1,2, MA Jinhui2*, HUANG Qiong2

1.Network Information Center, Chongqing Industry School, Chongqing 400043, P.R. China; 2.Chongqing Key Lab of Mobile Communications, Chongqing University of Posts and Telecommunications, Chongqing 400065, P.R. China)

In today’s society, the demand for location-based services, especially indoor location services, is becoming more and more urgent. Using the indoor wireless signal intensity to locate, the location fingerprint method has the advantages of convenience, low cost, and so on. But it will take a lot of manpower and time to build a fine-grained fingerprint database. In order to improve the efficiency, this paper proposes a method for constructing the database based on improved Kriging interpolation. The simulated annealing algorithm is used to improve the theoretical variogram fitting accuracy, and then the signal strength at the unmeasured points is estimated with measurement data. Compared with the inverse distance weighted interpolation and traditional Kriging interpolation, experimental results show that this method can not only effectively improve the construction efficiency and precision of interpolation fingerprint database, but also reduce the artificial workload of fingerprint data acquisition by 50%.

indoor location; location fingerprint; Kriging interpolation; simulated annealing algorithm

Signal Strength Database Interpolation by Kriging for a Wi-Fi Indoor Positioning System[J].Sensors,2015,15(9):21377-21393.

10.3979/j.issn.1673-825X.2017.06.007

2017-05-04

2017-09-30

马金辉 mjh602@foxmail.com

重庆市科委重点产业共性关键技术创新专项(cstc2015zdcy-ztzx40008)

TP391

A

1673-825X(2017)06-0751-07

刘辉元(1971 -)，男，四川南部县人，重庆市工业学校高级讲师。主要研究方向为无线传输、定位导航、物联网等。E-mail: 1317791201@qq.com。

马金辉(1989 -)，男，河南周口人，硕士研究生。主要研究方向为室内定位、蓝牙传输、智能家居等。E-mail: mjh602@foxmail.com。

黄 琼(1971 -)，女，四川西昌人，硕士，重庆邮电大学教授。主要研究方向为无线通信、室内定位、物联网等。E-mail: 307519688@qq.com。

(编辑：魏琴芳)