运用模态叠加法研究扩张式消声器的传递损失
钟庭生,李亚光,圣小珍,肖新标,杜几平,刘谋凯
(西南交通大学 牵引动力国家重点实验室,成都 610031)
运用模态叠加法研究扩张式消声器的传递损失
钟庭生,李亚光,圣小珍,肖新标,杜几平,刘谋凯
(西南交通大学 牵引动力国家重点实验室,成都 610031)
采用声学模态叠加法建立单腔扩张式消声器传递损失计算模型,然后通过Matlab编程实现单腔扩张式消声器传递损失的数值计算。在此基础上,比较声学模态叠加法、有限元法和基于平面波假定的经典公式法在计算单腔扩张式消声器传递损失上的差别,研究单腔扩张式消声器膨胀段尺寸对传递损失的影响。结果表明,对于平面入射波,声学模态叠加法可用于单腔扩张式消声器各频段传递损失的计算;增大膨胀段的半径能有效提高低频段的传递损失,但对高频段的影响较小;随着膨胀段宽度的增大,传递损失的峰值向低频移动,传递损失最大的频段向高频移动。
声学;单腔扩张式消声器;声学模态叠加法;传递损失;Matlab
飞机和汽车发动机的进排气系统、建筑物的通风和空调系统由许多管路组成,管路在换气、输送冷热气体的时候,也会传播噪声。消声器主要用于消除管道中的噪声,一般可以分为抗性消声器和阻性消声器两大类[1]。抗性消声器主要以声抗性原理使原在管道中传播的噪声遇到加装的消声器后,被反射回去,而不是将传播中的噪声能量消耗掉[1]。因为它具有明显的频率选择特性,所以特别适用于在管道噪声的频谱中具有明显的峰值特征的情况,一般适用于低中频段[1]。扩张式消声器是工程上常用的抗性消声器,其原理是通过膨胀段来改变声波传播路径上的阻抗,从而使入射波发生反射,反射得越多,则传到下游段的透射波就越少,就越能达到降噪的目的。
消声器的传递损失定义为消声器出口无反射时,消声器进口处的入射声功率级与出口处的透射声功率级之差[2]。消声器的传递损失反映了其本身的声波传递特性,不受声源、管道系统的影响。基于对入射波、反射波和透射波均作平面波假定的单腔扩张式消声器的传递损失经典公式为

式中R1为管道半径,R2为膨胀段半径,L为膨胀段的宽度,k=ω/c为声波的波数,ω为声波的圆频率,c为声速。但是,如果入射波不是平面波,且其频率高于消声器的截止频率,则基于平面波假定的公式就不能用,这时需要用声学模态叠加法、声学有限元法、声学边界元法等方法来计算它的传递损失。
国内外学者对消声器的传递损失进行了大量研究,Davis等将一维解析法引入到扩张式消声器的计算当中,并且给出了消声器传递损失的计算公式[3]。Munjal等利用传递矩阵法计算了消声器的传递损失[4]。Miles采用多维解析法计算了消声器的传递损失[5]。Ji等应用边界元方法计算了考虑运流效应的消声器传递损失,对于尺寸较大的结构,提出了基于阻抗矩阵的子结构边界元法[6]。Selamet等应用模态匹配方法计算了扩张式消声器的传递损失[7]。Wu等通过建立扩张式消声器传递损失的理论模型,探讨了不同进口弯角对消声器声学性能的影响[8]。宫建国等利用声传递矩阵法,计算了消声器的传递损失,分析了汽车消声器的声学特性,讨论了不同参数对消声器声学性能的影响[9]。王键等利用有限元法分析了扩张比、内插管长度以及扩张腔的个数等因素对抗性消声器声学性能的影响,表明改进消声器的结构参数可以有效提高消声器的传递损失[10]。
本文采用声学模态叠加法建立单腔扩张式消声器传递损失的计算模型,然后利用有限元法和基于平面波假定的经典公式法来验证该模型,最后利用所建立的模型讨论膨胀段的尺寸参数对消声器传递损失的影响。
1 运用声学模态叠加法计算传递损失
1.1 基本假设[1]
为使问题简化,对媒质和声波过程作如下假设和简化:
(1)媒质为理想流体;
(2)没有声扰动时,媒质在宏观上是静止的,同时媒质是均匀的;
(3)声传播时,媒质中的稠密和稀疏过程是绝热的;
(4)媒质中传播的是小振幅声波,各声学量是一级微量。
1.2 基本参数
如图1所示,假设圆形截面单腔扩张式消声器上游段和下游段的半径为R1,膨胀段的半径为R2,宽度为L,各段的轴线共线且各段内壁均为光滑刚性壁面。管内声场用柱坐标(r,θ,z)来描述。

图1 单腔扩张式消声器示意图
对于管内频率为ω的简谐波,其声压和空气质点速度幅值均是θ的周期函数,周期是2π,可以利用傅里叶级数分解为所有环向谐波分量的叠加,即

其中m是环向谐波指数。
所以本文只考虑入射波是环向谐波指数为m、径向模态阶次为s的模态声波[1–2]。

式中κ1,s为上游段的第s(s=0,1,2,…,)阶径向波数,可通过式(4)求得,即κ1,s为式(4)中κ的第(s+1)个非负实根[1–2],为上游段的第s阶轴向波数为声波的波数,vi1z为上游段入射波的轴向速度,Jm为m阶柱贝塞尔函数。
1.3 传递损失计算
一般来说,膨胀段对上游段是一个声负载,下游段对膨胀段是一个声负载,因而会引起部分声波的反射和透射。设在上游段有一入射波pi1和一反射波pre1,膨胀段有一入射波pi2和一反射波pre2,而下游段无限延伸,仅有透射波pt3。入射波是环向谐波指数为m、径向模态阶次为s的模态声波,所以反射到上游段、在膨胀段和下游段中的波关于环向角度θ的变化规律不变,但关于径向r和轴向z的变化规律要改变,反射到上游段、在膨胀段和下游段中的波可以看成是相应的声学模态波的叠加。如图1所示,假定坐标原点取在上游段和下游段的接口处,可以写出以下五种波的声压和质点速度表达式。
(1)上游段各处声压p1和质点轴向速度v1z

式中N1为上游段反射波所取的模态波的阶数,An为系数,κ1,n为上游段的第n阶径向波数,为上游段的第n阶轴向波数,ρ0为空气密度,其它同上。
(2)膨胀段各处声压p2和质点轴向速度v2z
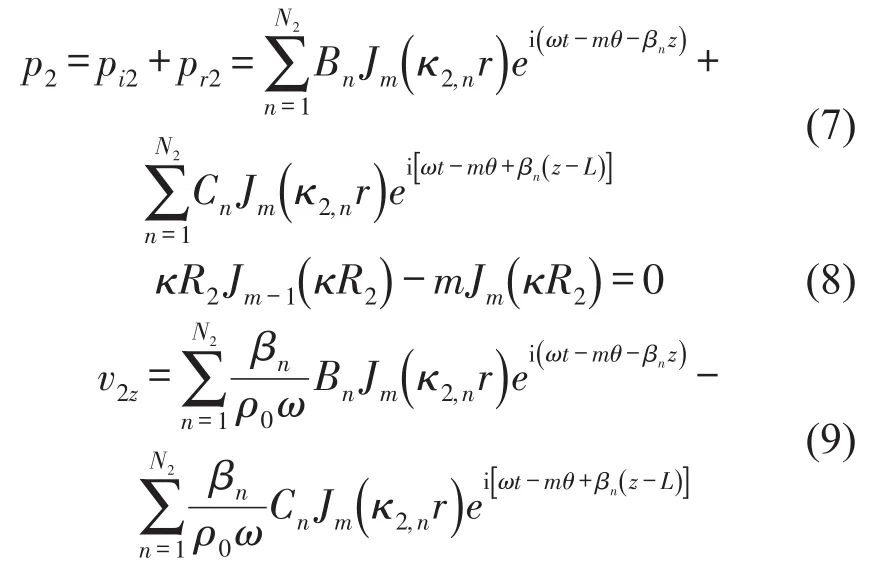
式中N2为膨胀段入射波和反射波所取的模态波的阶数,Bn、Cn为系数,κ2,n为膨胀段的第n阶径向波数,可通过式(8)求得,即κ2,n为式(8)中κ的第(n+1)个非负实根,为膨胀段第n阶轴向波数,其它同上。
(3)下游段各处声压p3和质点轴向速度v3z

式中Dn为系数,其它同上。
(4)边界条件
在上游段和膨胀段接口处(z=0)由声压连续条件得

将式(5)和式(7)代入式(12)得

由轴向质点速度连续条件得

将式(6)和式(9)代入式(14)得

在膨胀段和下游段接口处(z=L),由声压连续条件得

将式(7)和式(10)代入式(16)得

由轴向质点速度连续条件得

将式(9)和式(11)代入式(18)得

根据上下游段半径R1和需要计算的最大频率fmax从r=0到r=R1沿径向等间距(间距为dr)取N1个点,再从r=R1+dr到r=R2以同样的间距dr取(N2-N1)个点,再将这N2个点的径向坐标r(i)代入式(13)、式(15)、式(17)和式(19)得到 2(N1+N2)个含有2(N1+N2)个未知量的线性代数方程组,通过数值计算可求得这些未知量,再代入式(5)、式(6)、式(7)、式(9)、式(10)、式(11)即可得到不同位置的声压和质点轴向速度。
(5)计算传递损失
入射波和透射波的平均声功率分别为

单腔扩张式消声器的传递损失为

将式(3)代入式(20)得入射波的平均声功率,将式(10)、式(11)代入式(21)得透射波的平均声功率,再代入式(22)得单腔扩张式消声器的传递损失

2 数值计算与结果讨论
本文计算的单腔扩张式消声器各段内壁均为光滑刚性壁面,上下游段半径R1=0.05 m,空气密度ρ0=1.21 kg/m3,声速c=343 m/s,距离单腔扩张式消声器右端接口的距离Lz=0.01 m,只考虑入射波为平面波(m=0,s=0)的情况。
2.1 三种方法计算所得的单腔扩张式消声器传递损失的比较
图2给出了分别用声学模态叠加法、有限元法(LMS Virtural.Lab仿真计算)和基于平面波假定的经典公式法计算所得的单腔扩张式消声器传递损失的对比情况。其中膨胀段的截止频率上下游段的截止频率4 184Hz,单腔扩张式消声器的截止频率

图2 三种方法计算所得的单腔扩张式消声器传递损失的比较
由图2可知,对于平面入射波:
(1)声学模态叠加法与有限元方法计算所得的单腔扩张式消声器的传递损失基本一致,所以声学模态叠加法可用于计算单腔扩张式消声器在各频段的传递损失;
(2)低于单腔扩张式消声器截止频率时,起初声学模态叠加法与基于平面波假定的经典公式法计算所得的传递损失差别非常较小,随着频率接近fcut-off,差距增大;
(4)在频率小于单腔扩张式消声器的截止频率fcut-off之前,除了平面波外主要是非传播的高次波在起作用,且随着频率接近fcut-off,峰值向右偏移量越大,峰值的高度也有所增加,在频率大于fcut-off时,可传播的行波模式的高次波开始起作用,平面波下的传递损失的周期规律不复存在。
2.2 膨胀段半径对传递损失的影响
图3给出了膨胀段半径R2对单腔扩张式消声器(L=0.3 m)传递损失的影响云图。其中膨胀段截止频率最小的单腔扩张式消声器(R2=0.2 m)的截止频率fcut-off-R2=3.832c∕2 πR2=1 046Hz ,上下游段的截止频率fcut-off-R1=3.832c∕2 πR1=1 046Hz ,截止频率最小的单腔扩张式消声器的截止频率fcut-off-R=min(fcut-off-R1,fcut-off-R2)=1 046Hz。

图3 膨胀段半径对单腔扩张式消声器传递损失的影响
由图3可知,单腔扩张式消声器的其他参数不变的情况下,对于平面入射波:
(1)低于截止频率最小的单腔扩张式消声器的截止频率前一个零点频率可用([2Lfcut-off-R/c]c/2L)来估算时,消声器的传递损失随着膨胀段半径的增大而增大;
(2)在消声器上下游段截止频率内,膨胀段半径对消声器的传递损失的影响较大,但随着频率的增大膨胀段半径对消声器传递损失的影响越来越小,高出一定频率后,膨胀段半径对消声器的传递损失基本没影响;
(3)低于消声器的截止频率的峰值频率不随膨胀段半径变化而变化。
2.3 膨胀段宽度对传递损失的影响
图4给出了膨胀段宽度L对单腔扩张式消声器(R2=0.08 m )的传递损失的影响云图。

图4 膨胀段宽度对单腔扩张式消声器传递损失的影响
由图4可知,单腔扩张式消声器其他参数不变的情况下,对于平面入射波:
(1)随着膨胀段宽度的增大,消声器传递损失的峰值向低频移动;
(2)随着膨胀段宽度的增大,消声器传递损失最大的频段向高频移动。
2.4 膨胀段宽度与膨胀段半径的比值对传递损失的影响
图5给出了膨胀段宽径比L/R2对单腔扩张式消声器(R2=0.08 m,Lz=0.01 m )的传递损失的影响曲线。
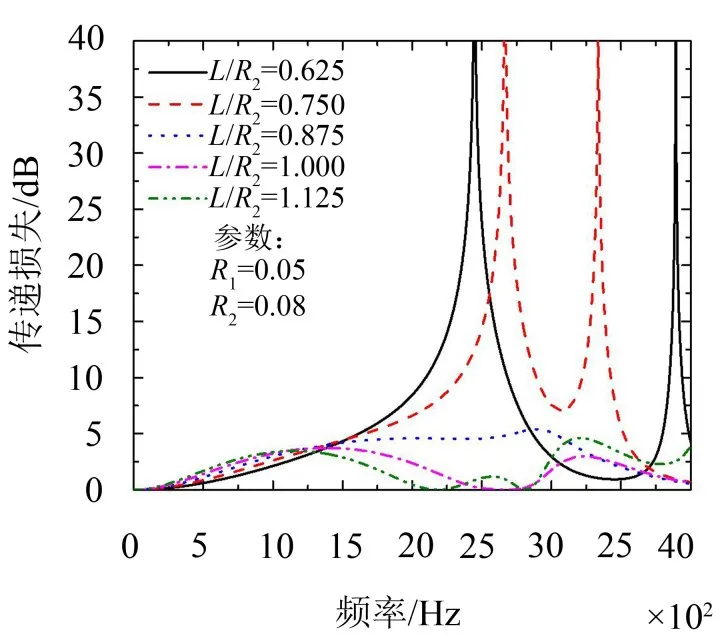
图5 膨胀段宽径比对单腔扩张式消声器传递损失的影响
由图5可知,当L/R2<0.82时没有完整的近似周期存在。根据基于平面波假定的经典公式可知,出现峰值的频率为


所以只有当L∕R2>0.82时才可能出现完整的周期,模态叠加法的结果与此吻合。
3 结语
本文利用声学模态叠加法计算了扩张式消声器的传递损失,并与有限元法和基于平面波假定的经典公式法计算结果进行比较,研究了消声器膨胀段的尺寸对其传递损失的影响。对于平面入射波,研究表明:
(1)基于平面波假定的经典公式法只能用于计算单腔扩张式消声器低于其截止频率时的传递损失,频率低于时,不但能简化计算还能得到较好的结果,声学模态叠加法(入射波可以是模态波)可用于计算单腔扩张式消声器各频段的传递损失,且可通过数值计算来辅助单腔扩张式消声器降噪的设计;
(3)随着单腔扩张式消声器膨胀段宽度的增大,消声器传递损失峰值向低频移动,消声器传递损失最大的频段向高频移动,可以通过改变膨胀段宽度来使其传递损失较大的频段包含噪声源的主要频段,从而达到降噪的目的。
[1]何琳,朱海潮,邱小军,等.声学理论与工程应用[M].北京:科学出版社,2006:145-153.
[2]季振林.消声器声学理论与设计[M].北京:科学出版社,2015:14-37.
[3]DAVIS D D,STOKES G M,MOORE D,et al.Theoretical and experimental investigations of mufflers with comments on engine exhaust muffler design[R].NACA,1192.Washington,DC,United States:US Government Printing Office,1954.
[4]MUNJAl M L.Veocity ratio-cum-transfer matrix method for the evaluation of a muffler with mean flow[J].Journal of Sound and Vibration,1975,39(1):105-119.
[5]MILES J.The reflection of sound due to a change in cross section ofacirculartube[J].TheJournalofthe Acoustical Society ofAmerica,1994,16:14-19.
[6]JI Z L,MA Q,ZHANG Z.Application of the boundary element method to prediction acoustic performance of expansion chamber mufflers with mean flow[J].Journal of Sound and Vibration,1994,173(1):57-71.
[7]SELAMET A,JI Z L.Acoustic attenuation performance of circular expansion chambers with offset inlet/outlet:I.Analytical approach[J].Journal of Sound and Vibration,1998,213(4):601-617.
[8]WU C H,WANG C N.Attenuation for the simple expansion chamber muffler with a right angle inlet[J].Journal of Mechanics,2011,27(3):287-292.
[9]宫建国,马宇山,崔巍升,等.汽车消声器声学特性的传递矩阵分析[J].振动工程学报,2010,23(6):636-641.
[10]王键,陈凌珊.结构参数对抗性消声器消声性能的影响分析[J].小型内燃机与摩托车,2010,39(3):86-88.
[11]詹福良.Virtual.Lab Acoustics声学仿真计算从入门到精通[M].西安:西北工业大学出版社,2013.
Study on the Transmission Loss of an Expansion Muffler Using Modal Superposition Method
ZHONG Ting-sheng,LI Ya-guang,SHENG Xiao-zhen,XIAO Xin-biao,DU Ji-ping,LIU Mou-kai
(State Key Laboratory of Traction Power,Southwest Jiaotong University,Chengdu 610031,China)
The acoustic modal superposition method is used to establish the trasmission loss calculation model for the single chamber expansion muffler.Its transmission loss is computed through Matlab programming.On this basis,the difference of the acoustic modal superposition method,the finite element method and the classical formula method in calculating the transmission loss of the single chamber expansion muffler is found.The influence of the size of the single chamber expansion muffler on the transmission loss is studied.The research indicates that,for the incident plane wave,the acoustic mode superposition method can be used to calculate the transmission loss of the single chamber expansion muffler in whole frequency range.Increasing the radius of the expanding section can effectively raise the transmission loss in low frequency range,but has small influence on the transmission loss in high frequency range.With increasing of the width of the expansion section,the peak values of the transmission loss shift to low frequency side and the frequency band of the maximum transmission loss moves to the high frequency side.
acoustics;single chamber expansion muffler;acoustic modal superposition;transmission loss;Matlab
TB535+.1
ADIO编码10.3969/j.issn.1006-1355.2017.06.041
1006-1355(2017)06-0206-05+215
2017-07-01
钟庭生(1990-),男,江西省赣州市人,硕士研究生,主要研究方向为轨道交通振动与噪声。
圣小珍,男,博士生导师。E-mail:shengxiaozhen@hotmail.com

