自然激励技术在时延相关白噪声激励系统中的应用

纪红刚，宋汉文

(1.广东省珠海市质量计量监督检测所，广东 珠海 519000；2.同济大学 航空航天与力学学院，上海 200092)

自然激励技术在时延相关白噪声激励系统中的应用

纪红刚1，宋汉文2

(1.广东省珠海市质量计量监督检测所，广东 珠海 519000；2.同济大学 航空航天与力学学院，上海 200092)

工况模态分析（operational modal analysis，OMA）是一种只基于输出数据进行系统模态参数辨识的技术。由于系统所受激励未知，通常假设其为互不相关的白噪声。自然激励技术（natural excitation technique，NExT）正是一种基于该假设的从响应数据中提取自由衰减信号的高效方法。然而对于真实工况，系统所受激励之间互不相关的假设过于严格，例如行驶的车辆等所受激励为时间延迟相关的白噪声。针对这类情况，基于复模态系统讨论NExT理论的适用性。结果表明，NExT是否适用取决于从相关函数中截取的用来进行OMA分析的数据段的位置，当数据段位于T＞ε区间内，NExT是适用的。在ε已知的情况下，可以基于NExT对系统进行工况模态分析。最后通过仿真进一步验证该结论。

振动与波；工况模态分析；自然激励技术；脉冲响应函数

有些研究对象或者无法施加人工激励，如在轨飞行器，或者人工激励代价昂贵或有破坏性，如桥梁、高耸结构、海洋平台，或者结构在工作状态下自身承受的环境激励不可测控，如机翼颤振、桥梁风振、机床切削颤振以及地震等情形，如何直接利用工况条件下的响应数据提取其模态参数，得到了众多学者的关注[1–3]。工况模态分析（Operational Modal Analysis，OMA）的提出及发展解决了激励不易获取的难题，它是一种只基于输出数据进行系统模态参数辨识的技术。

在OMA情形下，激励力是不可知的，通常假设为白噪声。基于该假设，James III提出了自然激励技术（natural excitation technique，NExT）[4–7]，该理论指出单输入白噪声激励下系统位移响应的互相关函数含有结构的各阶模态信息，并且证明了相关函数与系统脉冲响应函数具有相似的表达形式，可用于模态参数的时域辨识。这为环境激励下系统模态参数的提取提供了一条新的途径[8–10]。对于多输入情况下系统受环境激励时位移响应的互相关函数的数学表达以及模态参数辨识，钟军军等进行了研究[11–12]。对于NExT在复模态系统中的适用性，韩海明，秦飞等进行了一系列的探索[13–14]。

这些使用NExT理论进行模态参数辨识的工作，均是基于系统所受激励为互不相关的白噪声这一假设，该假设过于严格。在实际工况中，有些激励并不是完全互不相关的，例如列车行进时，后轮受到的路面激励与前轮始终有一个时间差，可以认为他们所受的激励是时间延迟相关的白噪声[15]。本文在NExT理论基础上，基于复模态系统的位移响应，探讨系统在受时间延迟相关白噪声激励下响应的相关函数与该系统单位脉冲响应函数之间的关系。以激励延迟的时间大小ε为分界点，分T＞ε以及0＜T＜ε两种情况，讨论了NExT理论的适用性。结果表明当从相关函数所截取的用于工况模态分析的数据段在T＞ε区间时，NExT是适用的；而数据段在0＜T＜ε区间时，NExT已经不可用。因此，在ε已知的情况下，可以基于NExT对系统进行工况模态分析。最后通过仿真证实了这一结论。

1 自然激励技术

N自由度线性时不变复模态系统强迫振动方程为

式中[M]、[C]和[K]分别为系统质量、阻尼和刚度矩阵；{x(t)}为系统稳态位移响应；{f(t)}为作用在系统上的激励。

如果系统在k点受的激励为fk(t)，则第i测点的响应为

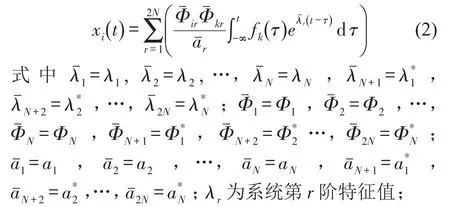
{Φ}r为系统的第r阶模态振型；diag为系统矩阵关于复振型在2N空间加权正交得到的矩阵；*为共轭运算。

当式(2)中的f(t)为在t=0处的单位脉冲函数即δ(t)函数时，就得到系统在k点激励i测点响应的单位脉冲响应函数hik(t)

若激励不只作用在k点，而是在L个激励点上都有，根据线性系统的叠加性，由式(2)可得i测点的响应为

第j测点响应的表达式同式(4)。由相关函数的定义，第i、j测点响应的相关函数Rij(T)可以写为

式中

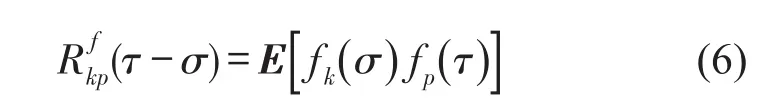
式中E[]为期望运算。

当f(t)为高斯白噪声时，f(t)的自相关函数为

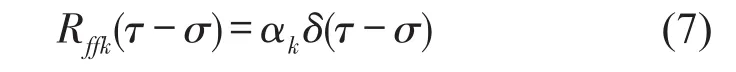
式中αk为常数，表示白噪声激励的强度。

假定在不同的激励点上，系统受的高斯白噪声激励互不相关，那么激励的相关函数将化简为

将式(8)及式(7)代入式(5)中，并利用δ(t)函数的性质进行化简得

2 时间延迟相关的白噪声

对于车辆一类的系统，正常前进时，后轮将间隔一定的距离，经历前轮所走过的路。这个空间上的距离在时间上体现为延迟。为描述这一情况，设系统在l和m激励点受到的白噪声激励分别为fl(t)和fm(t)，其中fl(t)与fm(t)有一个时间差ε，即

根据高斯白噪声的性质有

将式(11)及式(12)代入到式(5)得

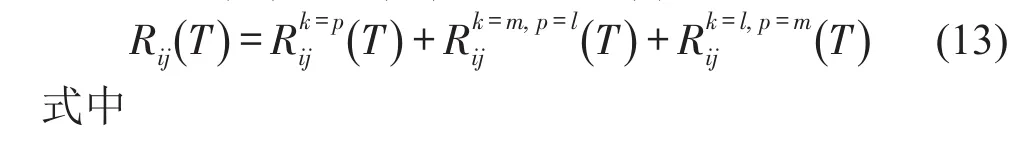
根据δ函数的性质，并注意积分的上下限，可以消去里面的一重积分。讨论σ及τ的积分上下限：

1.当T＞ε时，

此时，式(13)可以写为

2.当0＜T＜ε时，

此时，式(13)可以写为

对式(17)求积分得

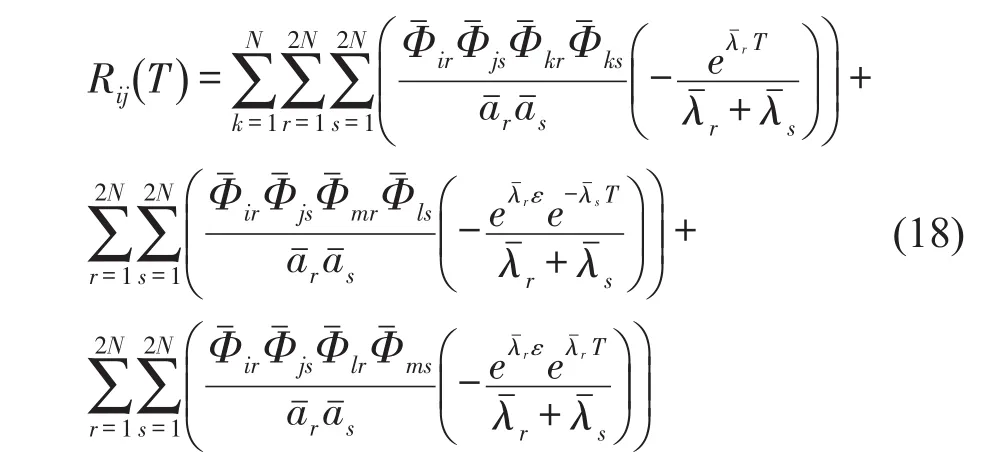
注意到式(18)中的第二项不是衰减的正弦波的叠加，不能写成与脉冲响应函数相似的表达形式，因此NExT理论在此时不再适用。

综上所述，受时延相关白噪声激励系统的响应的相关函数与系统的单位脉冲响应函数在0＜ε＜T时，不能写成与脉冲响应函数相似的表达形式，NExT理论在此时不再适用；但是在T＞ε时有着相似的表达形式，NExT理论依然适用。因此在已知ε的情况下，可以在工况下对结构系统进行模态分析。

3 仿真算例

如图1所示为6自由度系统。

图1 仿真系统

图1中，质量矩阵、刚度矩阵、阻尼比矩阵分别为

f1(t)为服从N(0,8080)的高斯白噪声，其余力为0。f3(t)与f1(t)的相关函数Rf3,f1如图1所示。

图2只给出了Rf3,f1的前3 s曲线，从图中可以看出f3(t)滞后f1(t)的时间为1 s。

将f1(t)及f3(t)作用在系统上，采集系统响应作响应的相关函数，取第1 s至第2 s之间的数据段进行工况模态分析。稳态图如图3所示。

从图3中可以清晰地看到6阶模态。将仿真给定的频率与辨识的频率进行比较，如表1所示。

从表1可以看到，频率辨识的可信度非常高。另外，辨识的振型如图4所示，为了便于比较，将给定的振型与辨识的振型均按其2-范数进行归一化处理。

在图4中，粗虚线为给定的系统固有振型，细实线为辨识的固有振型。粗虚线与细实线吻合得很好。

表1和图4表明，系统在受时延相关的白噪声激励时，在已知时延大小ε时，基于NExT进行工况模态分析是正确合理的。

图2 f3(t)与f1(t)的相关函数Rf3,f1

图3 工况模态分析稳态图

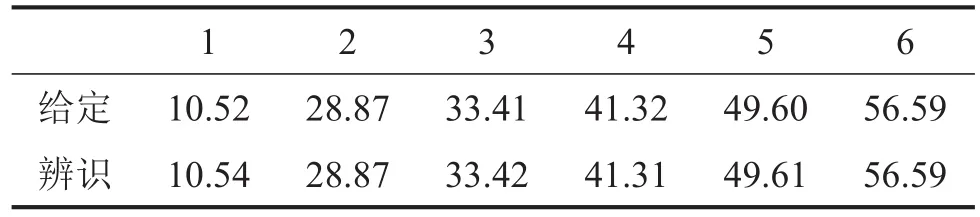
表1 给定的与辨识的固有频率/Hz

4 结语

本文在自然激励技术的基础上，基于复模态系统讨论了受时间延迟相关白噪声激励下系统单位脉冲响应函数与响应的相关函数之间的关系。给出了NExT的适用性条件，即从相关函数中所取的用于OMA分析的数据段需位于T＞ε区间。并且在已知激励间时间延迟ε的情况下，基于NExT对系统进行了工况模态分析。本文的方法进一步拓展了NExT的适用范围，具有一定的工程意义。

[1]BRINCKER R.Some elements of operational modal analysis[J].Joural of Shock and Vibration,2014,2014(4):1-11.

[2]刘志红，仪垂杰，尹志宏.多变量AR建模方法在工作模态参数辨识中的应用[J].噪声与振动控制，2007，27(4)：19-21.

图4 给定的与辨识的固有振型

[3]BRINCKER R,VENTURA C.Introduction to Operational Modal Analysis[M].New York:John Wiley and Sons,2015.

[4]JAMES G H,CARNE T G,VEERS P S.Damping measurements using operational data[J].Journal of Solar Energy Engineering,1996,118(3):190-193.

[5]JAMES III G H,CARNE T G,LAUFFER J P.The natural excitation technique (NExT) for modal parameter extraction from operating structures[J].Modal AnalysistheInternationalJournalofAnalyticaland Experimental ModalAnalysis,1995,4(10):260-277.

[6]JAMES III G H,CARNE T G,LAUFFER J P.The natural excitation technique (NExT) for modal parameter extraction from operating wind turbines[J].NASA STI/Recon Technical Report N,1993,93(4):260-277.

[7]JAMES G H.Extraction of modal parameters from an operating HAWT using the Natural Excitation Technique(NExT)[A].Proceedings of the 13th Energy-Sources Technology Conference and Exhibition(ETCE)on Wind Energy[C].New Orleans,Louisiana,USA:1994:23-26.

[8]李雷.工况模态分析在时变航天器结构中的应用[D].上海：复旦大学，2011.

[9]CARNE T G,JAMES G H I.The inception of OMA in the development of modal testing technology for wind turbines[J].Mechanical Systems and Signal Processing,2010,24(5SI):1213-1226.

[10]BROWNJOHN J M W,MAGALHAES F,CAETANO E,et al.Ambient vibration re-testing and operational modal analysis of the Humber Bridge[J].Engineering Structures,2010,32(8):2003-2018.

[11]钟军军，董聪.多自由度系统自然激励技术的统一模型[J].计算力学学报,,2013，30(3)：449-454.

[12]钟军军，董聪.单输入多自由度系统自然激励技术的解析格式[J].振动、测试与诊断，2013，33(4)：547-549.

[13]韩海明，沈涛虹，宋汉文.工况模态分析的EMD方法[J].振动与冲击，2002(4)：71-73.

[14]秦飞，宋汉文，王文亮.基于现代谱估计理论的工况模态分析[J].振动与冲击，2002(4)：74-79.

[15]ZHANG Y,ZHANG J.Numericalsimulationof stochastic road process using white noise filtration[J].Mechanical Systems and Signal Processing,2006,20(2):363-372.

Application of Natural Excitation Technique in the Structures under Time-delay-correlative White Noise Excitations

JI Hong-gang1,SONG Han-wen2
(1.Guangdong Zhuhai Supervision Testing Institute of Quality and Metrology,Zhuhai 519000,Guangdong China;2.School ofAerospace Engineering andApplied Mechanics,Tongji University,Shanghai 200092,China)

Operational modal analysis(OMA)is a technique for system modal parameter identification based on outputonly data.Since the excitation of the system is unknown,it is usually assumed to be an independent Gaussian white noise.The natural excitation technique(NExT)greatly promotes the development of OMA,which is an efficient method for extracting free attenuation response signals from output-only data.However,for real systems,the assumption of the independent excitations is over-strict.For example,the excitations of the traveling vehicles are time-delay-correlative white noises.Therefore,the applicability of NExT in this case is discussed based on the complex modal system.The results show that the applicability of NExT depends on the time delayε.When the data fragment cut from the correlation function of the system responses locates in the interval ofT＞ε,NExT is valid and otherwise,the NExT is invalid.Finally,a simulation is done to testify the conclusion.

vibration and wave;operational modal analysis(OMA);natural excitation technique(NExT);correlation function

O321；O327

A

10.3969/j.issn.1006-1355.2017.06.042

1006-1355(2017)06-0211-05

2017-04-14

纪红刚（1973-），男，吉林省人，工程师，主要研究方向为振动测试与模态分析。

宋汉文，男，教授，博士生导师。E-mail:hwsong@tongji.edu.cn