粒子滤波方法在转子典型故障诊断中的应用

刘晓强，荆建平，李亚伟，杨广振，贾 林

（1.上海电气电站设备有限公司 上海汽轮机厂，上海 201100；2.上海交通大学 机械系统与振动国家重点实验室，上海 200240；3.上海交通大学 船舰设备噪声与振动控制技术国防重点学科实验室，上海 200240；4.中国航发商用航空发动机有限责任公司，上海 200240）

粒子滤波方法在转子典型故障诊断中的应用

刘晓强1，荆建平2,3，李亚伟2，杨广振2，贾 林4

（1.上海电气电站设备有限公司 上海汽轮机厂，上海 201100；2.上海交通大学 机械系统与振动国家重点实验室，上海 200240；3.上海交通大学 船舰设备噪声与振动控制技术国防重点学科实验室，上海 200240；4.中国航发商用航空发动机有限责任公司，上海 200240）

转子的故障诊断是当前转子动力学的一个难点。针对这个问题，提出基于粒子滤波方法的转子典型故障诊断方法。针对Jeffcott转子建立不对中、裂纹和弯曲复合故障模型，并构建基于粒子滤波器的参数估计方程。通过在转子实验台上模拟故障对算法进行验证，结果表明：粒子滤波方法对于转子故障有较高的识别能力，可以诊断单一故障和多重故障。与传统的转子故障诊断方法相比，它不依赖于经验和故障事例，同时可较精确地估计故障参数。

振动与波；转子动力学；故障诊断；粒子滤波；参数估计

随着人们对旋转机械转速、效率的要求越来越高，旋转机械正朝着高速、轻型、大功率、大载荷方向发展，这可能导致各种故障的发生，如果不能及时发现和处理，会使机械设备可靠性降低、失去生产功能，造成数百万、上千万的经济损失，甚至会导致机毁人亡的重大事故。

当前对于转子故障的诊断基本是采用基于振动信号特征结合经验的诊断方法[1]，如轨迹诊断法、频谱诊断等，这些方法往往包含过多人为的判断。近些年虽出现了一些智能诊断方法[2]，如神经网络、专家系统等，但其诊断精度多依赖于大量的故障事例和故障数据，往往缺乏实际的可操作性[3]。而且，两种方法都很难诊断出复合故障。因此有必要寻求一种更为强有力的方法对故障实施有效的诊断和防治。

粒子滤波是一种基于蒙特卡罗思想的非线性、非高斯系统滤波算法[4–7]。它通过预测和更新来自于系统概率密度函数的采集，来近似非线性系统的贝叶斯估计，在处理非高斯、非线性时变系统的参数估计和状态滤波问题方面有独特的优势和广阔的前景。目前粒子滤波在目标定位与跟踪领域得到了深入研究，同时它在系统辨识、参数估计、自动控制以及动态系统中的故障诊断等领域也得到了广泛的应用。将粒子滤波方法应用到转子故障诊断中，不仅可以丰富转子故障诊断的手段，同时可以提高诊断能力。

1 转子模型

以本特利转子（见图1）为研究对象，将其视为Jeffcott转子（见图2）。

图1 本特利转子

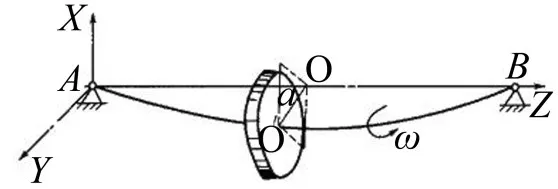
图2 Jeffcott转子

转子的质量、刚度和阻尼分别用m、c、k表示。转盘的不平衡量为e，转速为ω。通过实验和计算得到转子的系统参数如下：

集中质量：m=0.943 kg

阻尼系数：cx=12.33，cy=10.91N·s/m

刚度系数：kx=41 308，ky=37 043 N∕m

不平衡量：e=23.6 μm，θ0=335 °

噪声方差：R=3.6×10-3，Q=1×10-5

根据转子动力学的知识[8]，通过对转子典型单一故障进行归纳总结，建立起多故障状态下的转子运动微分方程。方程中x、y为圆盘中心在水平和竖直方向上的振动位移。

1.1 不对中故障模型

联轴器不对中包括了平行不对中和角度不对中，其统一的动力学方程如式(1)所示[9]

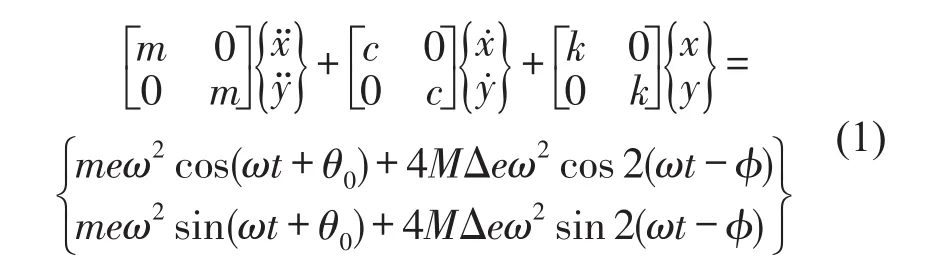
式中Δe、φ为故障参数不对中量大小和相位。

1.2 裂纹故障模型

对于裂纹转子的动力学行为分析，目前已有较多的模型。本文采用考虑裂纹开闭效应的方波模型如式(2)－式(4)所示[10]

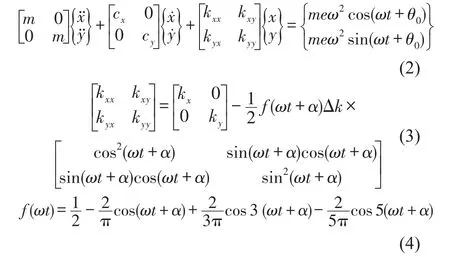
式中Δk、α为故障参数裂纹的大小和相位。

1.3 弯曲故障模型

转子弯曲包括了初始弯曲、热弯曲和摩擦热弯曲，其统一的运动微分方程为

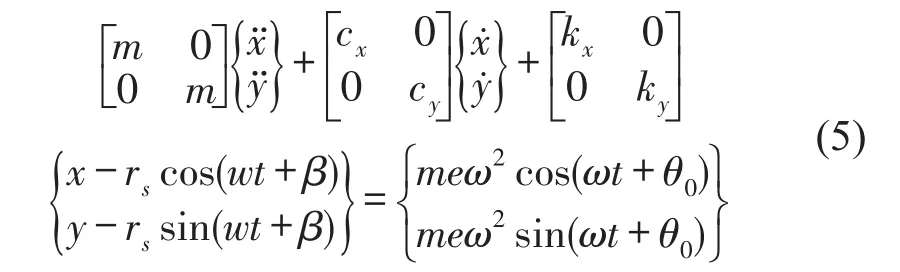
式中rs、β为转轴在圆盘处的弯曲量大小和相位。

1.4 复合故障模型

不对中故障主要表现为联轴器对转子系统所施加的附加弯矩；裂纹故障主要表现在对转轴刚度的影响上，引入了交变刚度；弯曲故障主要表现在转轴变形对弹力的影响上。同时考虑不对中、裂纹和弯曲三种故障，建立其复合故障对应的转子运动微分方程如下[11]

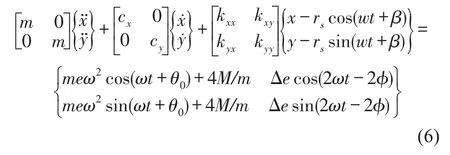
2 粒子滤波（PF）

2.1 粒子滤波算法

对于离散时间动态系统，均可用如下模型描述。

状态模型为xk=fk(xk-1,wk)

观测模型为zk=hk(xk,vk)

式中x为系统状态向量，z为系统输出向量；w和v为零均值白噪声向量序列，协方差分别为Q和R。

我们的目的是根据观测数据递推，估计出状态后验概率分布p(x0:k|Zk)，特别是滤波概率分布p(xk|Zk)，最终实现状态估计。Zk={z1,…,zk}表示直到k时刻的所有观测量。粒子滤波器的本质是用有限的样本近似任意状态的后验概率密度。k时刻的后验概率密度可以近似为

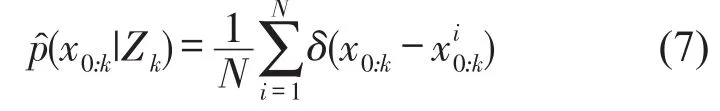
但从后验概率中很难直接采样，所以引入一种容易采样的已知概率分布函数q(x0:k|Zk)，称为重要性密度函数，该函数的选择也是粒子滤波器中的一个重要问题，一般选择状态转移概率密度函数p(xk|xk-1)作为重要性密度函数。

基本粒子滤波器的实现步骤如下所示（设定粒子数为N）：

（1）初始化取k=0，采样即根据先验概率p(x0)分布采样得到

（2）重要性权值计算。设定k:=k+1，采样

计算重要性权值如下

（5）判断是否结束，若是则退出本算法，否则返回步骤（2）。

2.2 重采样算法

重采样方法的基本思想是通过对后验概率密度再采样Ns次，产生新的支撑点集保留或复制具有较大权值的粒子，剔除权值较小的粒子[12–13]。

图3为重采样原理的示意图[14]。k-1时刻的先验概率密度由若干权值为N-1的粒子近似表示(图中仅画出10个粒子)，经过系统观测后(第一步)，重新计算粒子的权值较符合实际情况的粒子（即波峰处的粒子）被赋予较大的权值（图中表示为面积大的粒子），而偏离实际情况的粒子(即波谷处的粒子)被赋予较小的权值(图中表示为面积小的粒子)。第二步即是重采样过程，权值大的粒子衍生出较多的“后代”粒子，而权值小的粒子相应的“后代”粒子也较少，并且“后代”粒子的权值被重新设置为N-1。第三步是系统状态转移过程，预测每个粒子在k时刻的状态。第四步则是k时刻的系统观测过程，与第一步一致，并且通过若干粒子的加权得到目标状态的最终表示。

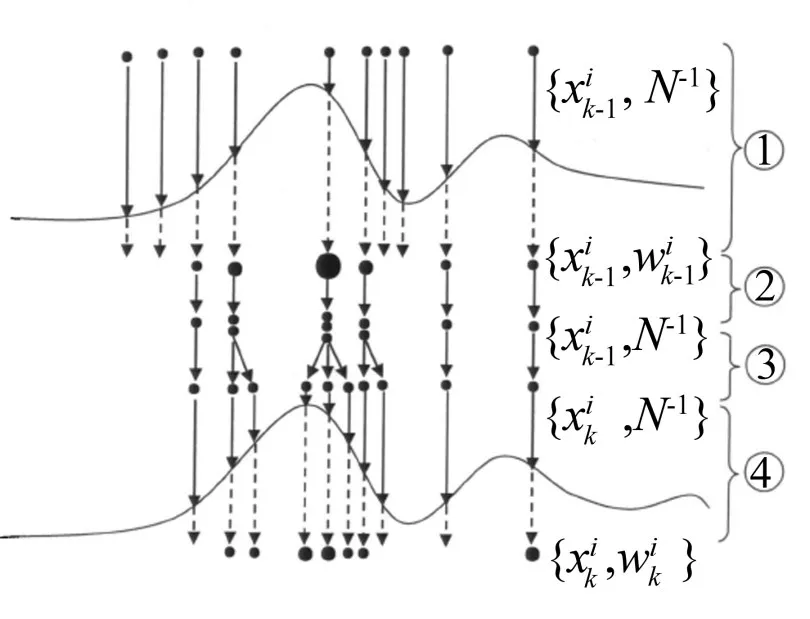
图3 重采样原理示意图

目前广泛应用的重采样算法包括多项式重采样算法、分层重采样算法、系统重采样算法、权值优选重采样算法。以上重采样算法在重采样过程中去掉权值小的采样点的同时仅复制了权值大的粒子，因而会造成粒子匮乏。线性优化重采样算法正是充分利用权值小的粒子进行重采样，其主要思想是：在需要重复某个采样点的时候，通过将该采样点和被抛弃的采样点进行适当的线性组合而产生新的采样点。线性组合方式如下

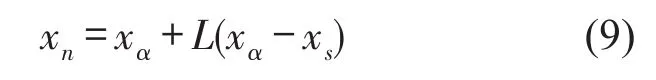
式中xn是通过组合方式产生的新采样点，xα为被重复选取的采样点，xs为被抛弃的采样点，L为(xα-xs)的合适步长。

设N为采样点个数，m为采样空间维数，ω为任一采样点领域空间内采样点的分布概率，则抛弃点到该点的合适步长为

3 粒子滤波在转子故障诊断中的应用

如果将待识别的转子故障参数作为状态向量来估计,那么就可以根据振动测量信号来识别转子的故障参数，判断是否具有故障以及具体故障的类型和严重程度。转子系统故障诊断实际上是通过对其运动微分方程中的故障参数做参数估计而实现的。粒子滤波算法运用在转子系统故障诊断时，需要注意以下几点：

首先，需要建立转子系统的运动微分方程，并将故障参数扩展到微分方程的状态变量中，建立参数估计方程。

其次，粒子滤波前需要选择合适的粒子数目和粒子初值。理论上粒子数目越多计算结果越精确，但是过多的粒子数目会降低计算速度，一般粒子数目满足允许的估计误差即可。粒子初值包括了状态初值和故障参数初值，状态初值指的是转子振动状态（位移、速度）值，一般选择满足测量信号初始值为均值、噪声协方差为方差的高斯分布数据（针对高斯噪声情况）；而故障参数初值一般根据经验选择或者根据均匀分布概率密度选择。

再次，在做粒子滤波运算时，为避免粒子的退化现象，需要选择合适的重采样算法。如果初始粒子数目足够且先验概率分布较为准确，适宜选择多项式重采样算法、分层重采样算法以及系统重采样算法。为了保证粒子的多样性，同时又不增加粒子数目，可以选择线性优化重采样算法。根据多重故障模型，构建对应的故障参数估计方程如式(11)。由于在短时间内故障参数是常数，所以其关于时间的导数值为0。在实际诊断中，参数估计方程中的转子系统参数选择为实际测量值[14]。

图4 不对中转子时基和频谱

4 实验验证

4.1 故障模拟

在本特利转子实验台上分别模拟多种故障。通过在联轴器结合面的局部安装垫片来模拟不对中故障；通过电火花加工裂纹轴来模拟裂纹故障；通过加工弯曲轴来模拟弯曲故障；通过在弯曲轴的基础上电火花加工裂纹来模拟弯曲裂纹复合故障。启动以上四种故障形式的转子，将转速分别稳定于1 200 r/min、300 r/min、720 r/min、300 r/min，测量不同故障形式下的圆盘处振动位移，其时基和频谱图如图4、图5、图6、图7所示。

从以上图可以看出不同故障的转子具有不同的时域和频域图，下面通过粒子滤波的方法来识别出不同的故障参数就可以进行故障诊断。

4.2 故障诊断

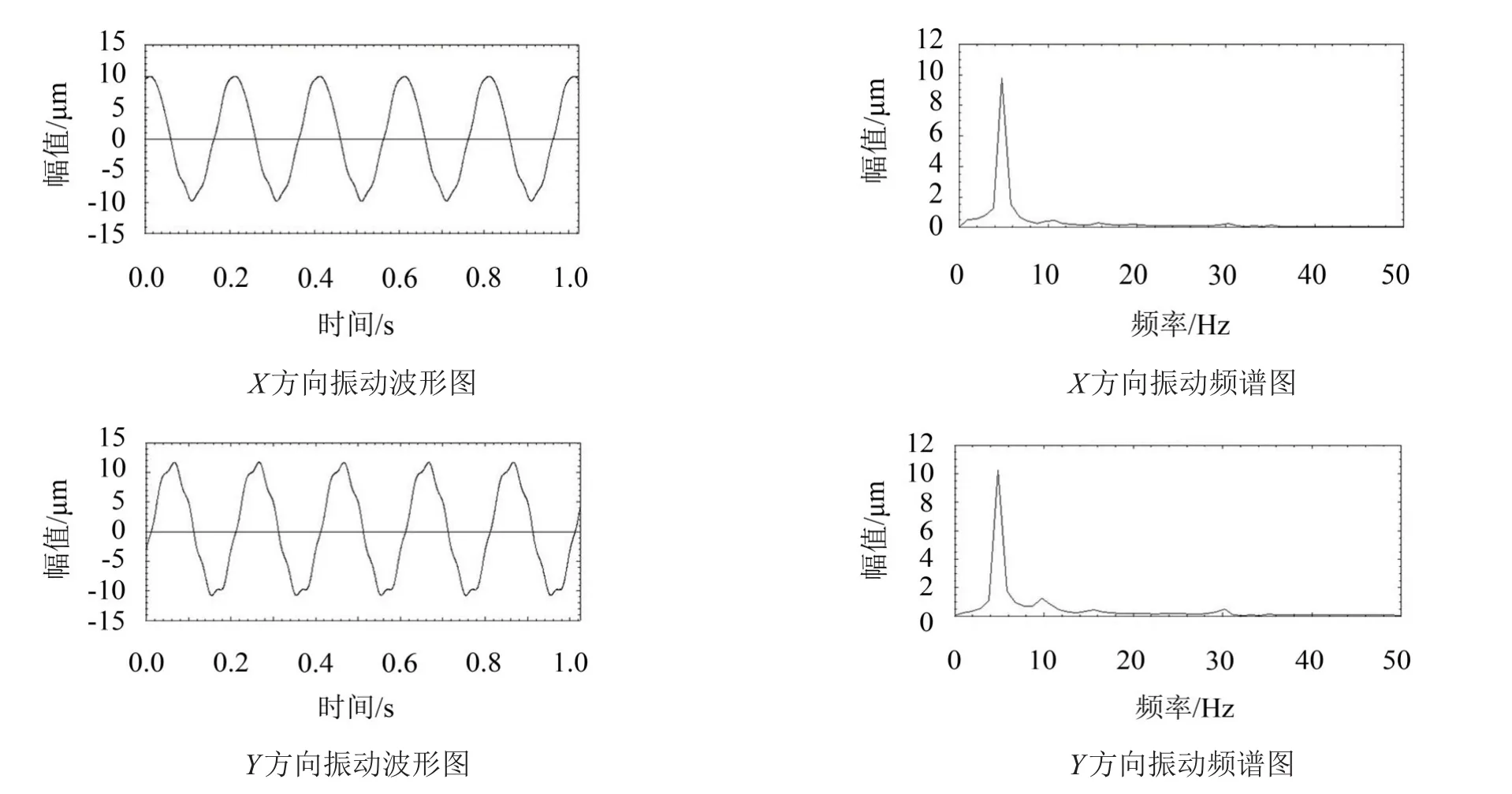
图5 裂纹转子时基和频谱

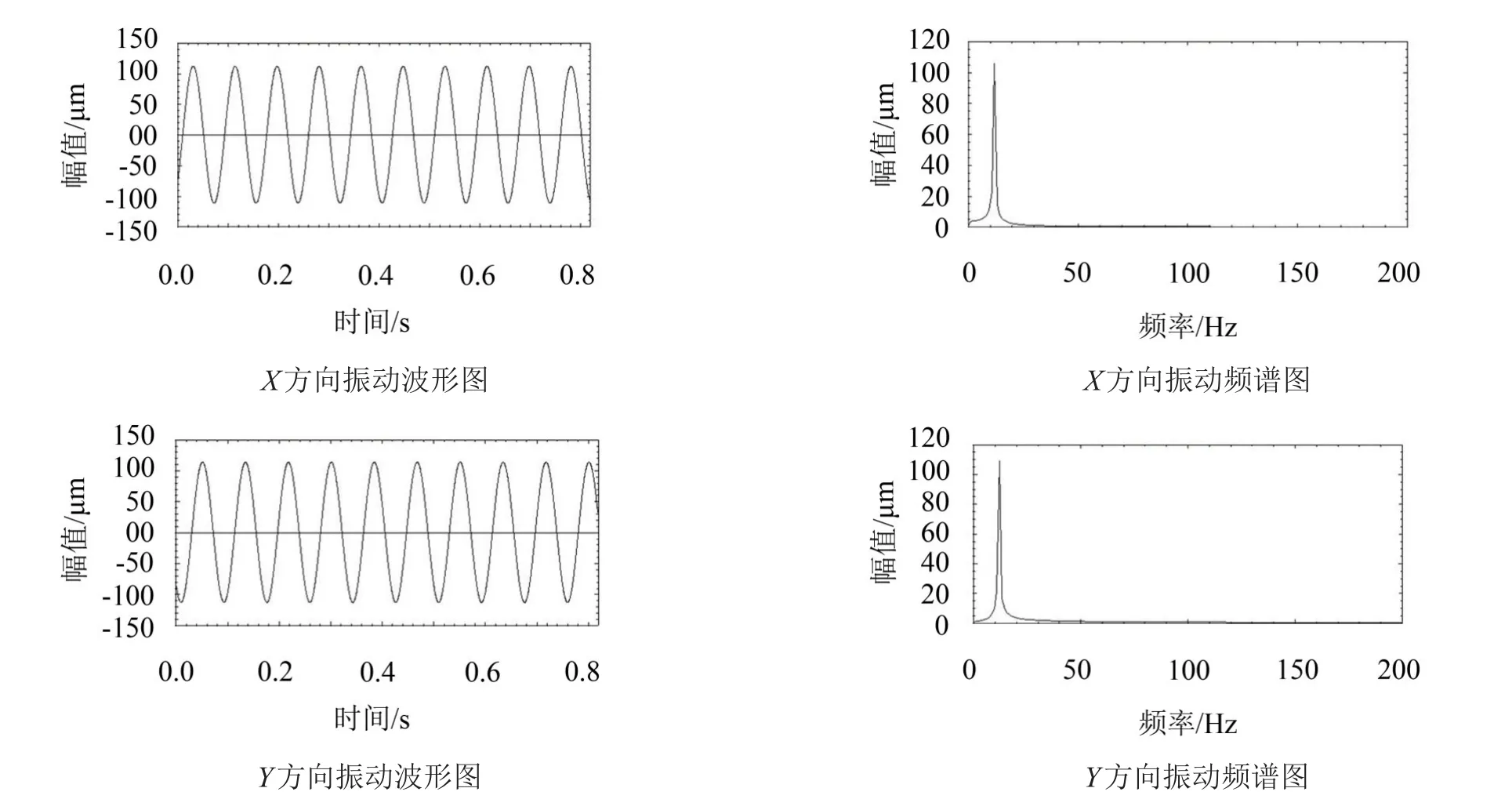
图6 弯曲转子时基和频谱

由于多故障转子系统故障参数增多,为了保证滤波结果的精确度，必须选择足够数目的粒子。但粒子数目过多会影响计算速度。这里，粒子数目选择为10 000，每个粒子初始权值相同。粒子的振动状态初值选择为高斯分布数据，其均值为以测量信号初始值[x(0),y(0),(x(1)-x(0))/T,(y(1)-y(0))/T]，方差为噪声协方差R。

粒子不对中参数Δe、ϕ分别选择为在区间上满足均匀分布的数据；裂纹参数Δk、α分别选择为在区间[0,0.3 k]、[0,2 π]上满足均匀分布的数据；弯曲参数γs、β分别选择为在区间 [0,200 μm]、[0,2π]上满足均匀分布的数据。这样初始化的粒子可以诊断出转子系统的单一故障和多重故障。

采用基于线性优化重采样的标准粒子滤波算法分别对不对中故障振动信号、裂纹故障振动信号、弯曲故障振动信号以及弯曲裂纹复合故障振动信号进行故障诊断。其诊断结果如下：

(1)不对中故障诊断结果

从粒子滤波结果（见图8）可以看出，经过有限步的计算，当量不对中量幅值Δe估计值收敛于19.6 μm，弯曲量幅值γs几乎收敛于0，而交变刚度幅值Δk收敛于1 047 N/m，约为转轴刚度的2.5%。交变刚度幅值没有收敛于0，是因为较小的交变刚度对转子的振动影响很小。计算结果说明了转子具有不对中故障。

(2)裂纹故障诊断结果

在数据获取层，主要的数据获取来源为制造设备的智能电器控制设备，可采集用电设备的负荷、室内温湿度、光线情况、人体活动情况等。各智能传感设备获取的数据通过第三方云数据平台汇总，传输到数据存储层。

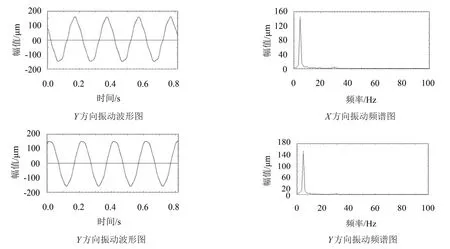
图7 弯曲裂纹复合故障波形图和频谱图

从粒子滤波结果（见图9）可以看出，经过有限步的计算，当量不对中量幅值Δe估计值几乎收敛于0，弯曲量幅值γs收敛于0，而交变刚度幅值Δk大约收敛于5 000 N/m，约为转轴刚度的12%。计算结果说明了转子具有裂纹故障。

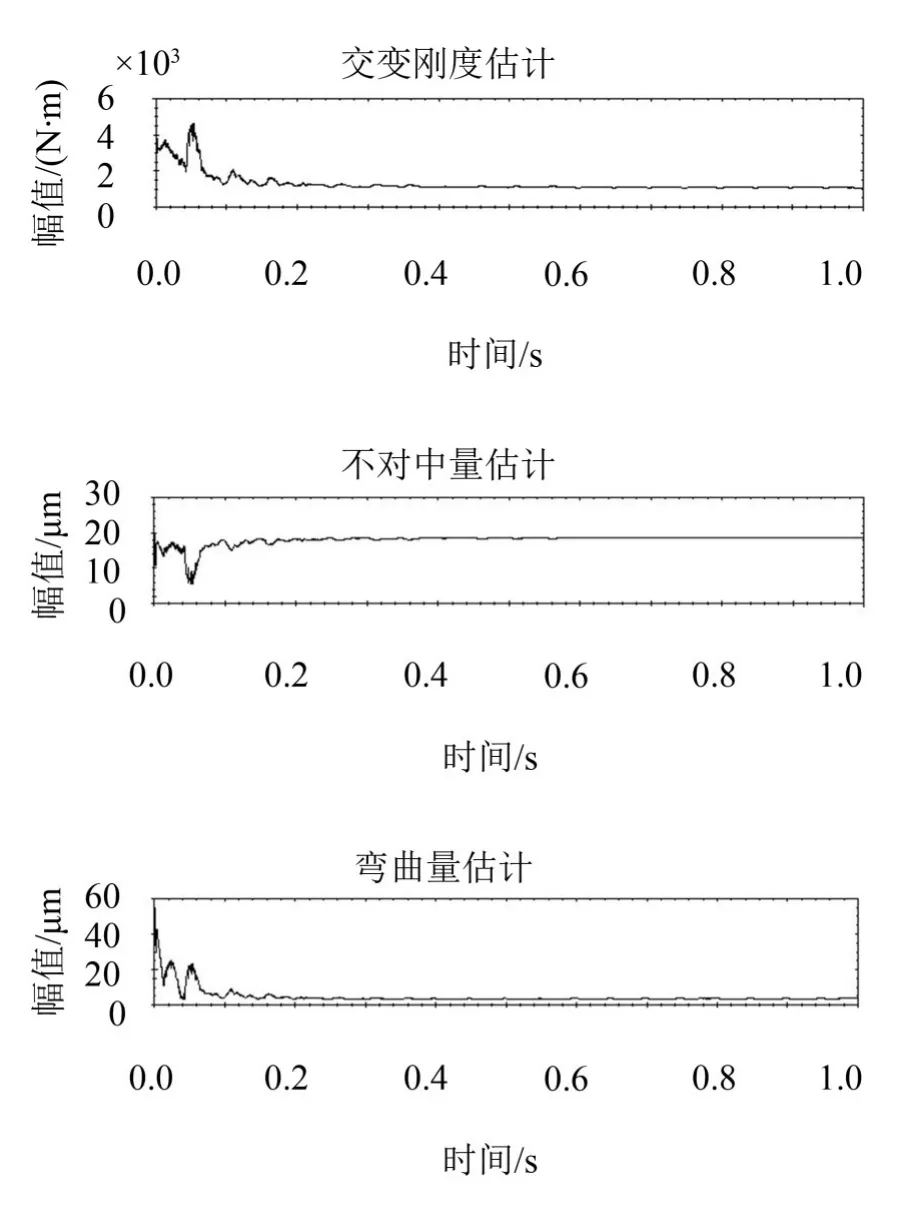
图8 不对中故障粒子滤波结果

(3)弯曲故障诊断结果

从粒子滤波结果（见图10）可以看出，经过有限步的计算，当量不对中量幅值Δe估计值几乎收敛于0，弯曲量幅值γs收敛于84.8 μm，而交变刚度幅值Δk收敛于1 415 N/m，约为转轴刚度的3.5%。同样，交变刚度幅值也没有收敛于0。计算结果说明了转子具有弯曲故障。

(4)弯曲裂纹复合故障诊断结果

图9 裂纹故障粒子滤波结果

从粒子滤波结果（见图11）可以看出，经过有限步的计算，当量不对中量幅值Δe估计值几乎收敛于0，弯曲量幅值γs收敛于86 μm，而交变刚度幅值Δk大约收敛于5 000 N/m，约为转轴刚度的12%。计算结果说明了转子同时具有弯曲故障和裂纹故障。

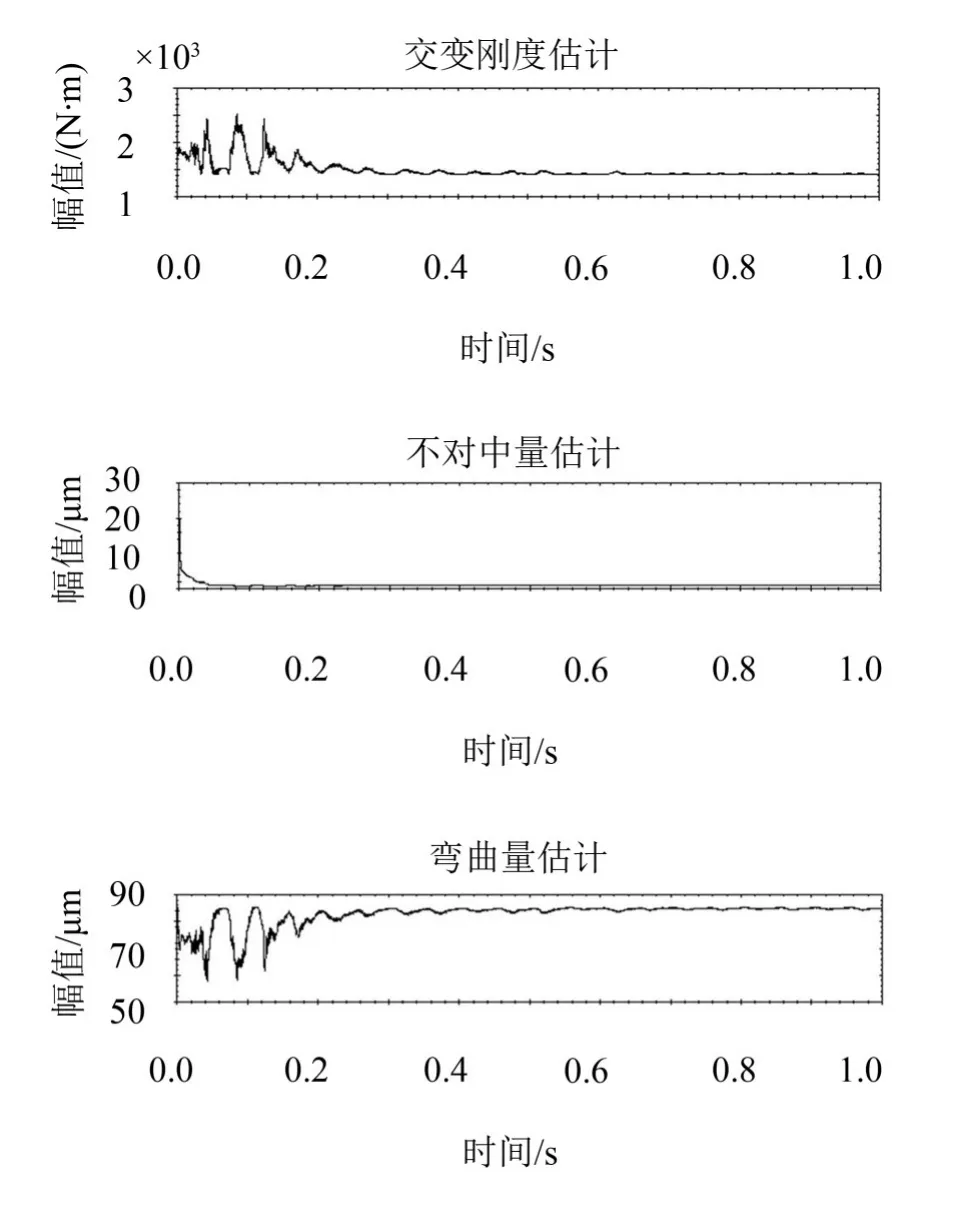
图10 弯曲故障粒子滤波结果

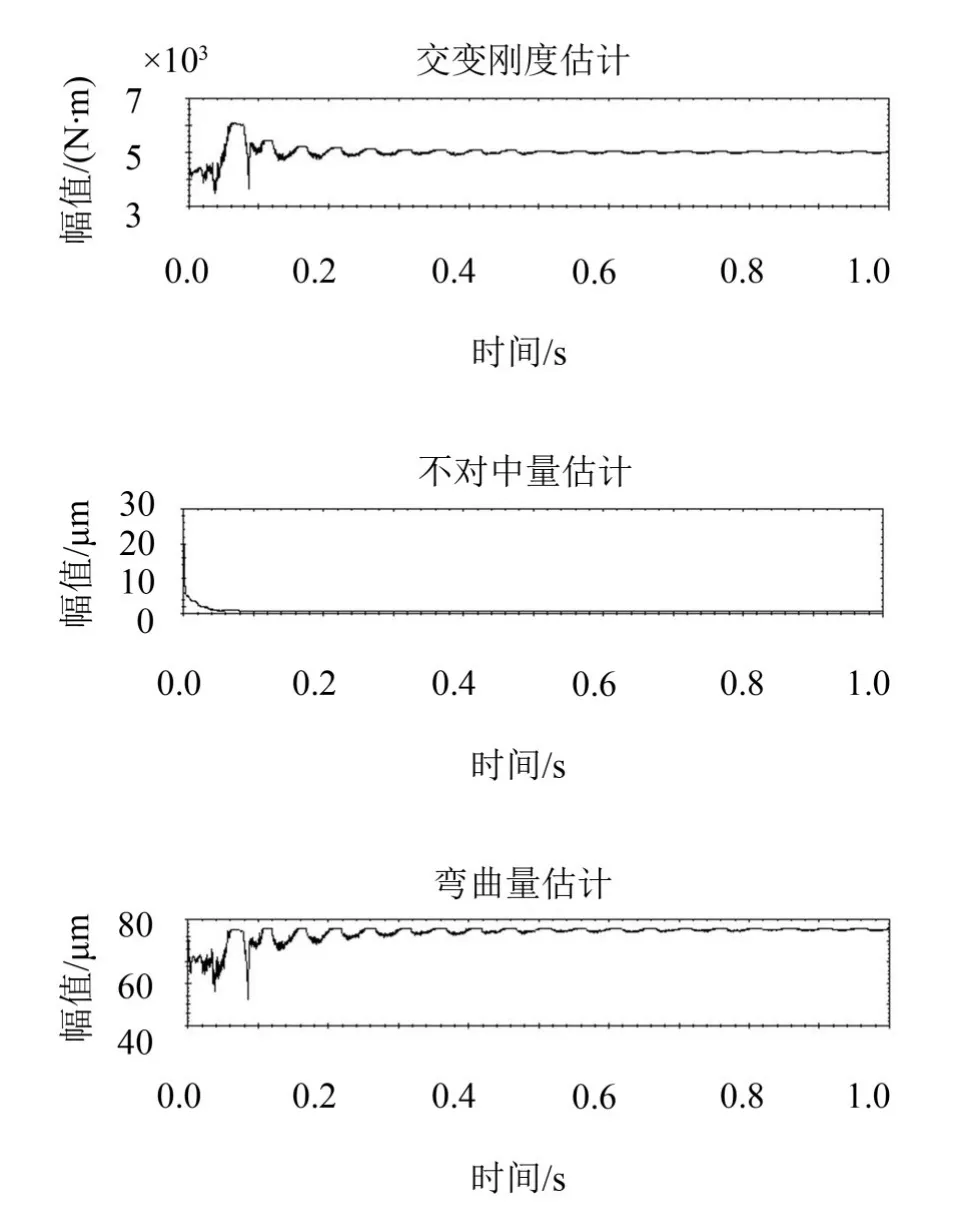
图11 弯曲裂纹故障粒子滤波结果

5 结语

针对Jeffcott转子，通过归纳总结不对中、裂纹和弯曲故障，建立起多重故障状态下的转子运动微分方程。根据多重故障模型，构建了基于粒子滤波的参数估计方程。在本特利转子上分别模拟不对中、裂纹、弯曲以及裂纹弯曲复合故障，对于参数估计方程应用粒子滤波算法实现对转子的故障诊断。结果表明：粒子滤波方法对于转子故障有着较强的识别能力，不仅可以诊断出单一故障，同时可以诊断多重故障。与传统的转子故障诊断方法相比，它不依赖于经验和故障事例。同时，可以较精确地估计故障参数，对旋转机械的安全运行起着很好的保障作用。

[1]陈进.机械设备故障诊断技术及其应用[M].上海：上海高教电子音像出版社，2003.

[2]何正嘉.机械设备非平稳信号的故障诊断原理及应用[M].北京：高等教育出版社，2002.

[3]荆建平,张传斌,孟光.基于多模型估计的转子裂纹故障诊断方法[J].汽轮机技术，2007，49(1)：1-4.

[4]DOUCET A,GORDON N,KRISHNAMURTHY VK.Particle filters for state estimation of jump markov linear systems[J].IEEE Trans.on Signal Processing,2001,49:613-624.

[5]CHEN T,MORRIS J,MARTIN E.Particle liters for the estimation of a state space model[C].Proceedings of European Symposium on ComputerAided Process Engineering,2004,(13):131-140.

[6]吴宝成.粒子滤波重采样算法研究及其应用[D].哈尔滨：哈尔滨工业大学，2007.

[7]冯驰，王萌，汲清波.粒子滤波器重采样算法的分析与比较[J].系统仿真学报，2009，21(4)：1101-1105.

[8]闻邦椿.高等转子动力学：理论、技术及应用[M].北京：机械工业出版社，1998.

[9]黄志伟，周建中，张勇传.水轮发电机组转子不对中-碰摩耦合故障动力学分析[J].中国电机工程学报，2010(8)：88-93.

[10]邹剑，陈进，董广明.含初始弯曲裂纹转子振动特性[J].上海交通大学学报，2004，38(7)：1218-1221.

[11]李振平.多故障转子系统若干非线性问题的研究[D].沈阳：东北大学，2002.

[12]杨珺.粒子滤波算法研究及应用[D].西安：西安理工大学，2008.

[13]冯驰，王萌，汲清波.粒子滤波器重采样算法的分析与比较[J].系统仿真学报，2009(4)：1101-1105.

[14]贾林.基于多模型估计的转子典型故障诊断与参数识别方法研究[D].上海：上海交通大学，2013.

Application of Particle Filter Method to Typical Rotor Fault Diagnosis

LIU Xiao-qiang1,JING Jian-ping2,3,LI Ya-wei2,YANG Guang-zhen2,JIA Lin4
(1.Shanghai Turbine Company,Shanghai Electric Power Station Equipment Co.Ltd.,Shanghai 201100,China;2.State Key Laboratory of Mechanical System and Vibration,Shanghai Jiaotong University,Shanghai 200240,China;3.Defense Key Disciplines Laboratory of Ship Equipment Noise and Vibration Control Technology,Shanghai Jiaotong University,Shanghai 200240,China;4.AECC CommercialAircraft Engine Co.Ltd.,Shanghai 200240,China)

The rotor fault diagnosis is a difficult problem of rotor dynamics.In this paper,the Particle Filter(PF)based method for typical rotor fault diagnosis is proposed.The model for a Jeffcott rotor with misalignment fault,crack fault and bending fault is built.Based on the model,the equation for fault parameter estimation is set up based on the PF.Via the fault simulation on Bently rotor,it is proved that this proposed method is effective in both single and multiple fault diagnosis.Meanwhile,it can estimate the fault parameters precisely.

vibration and wave;rotor dynamics;fault diagnosis;particle filter;parameter estimation

TH212；TH213.3

A

10.3969/j.issn.1006-1355.2017.06.035

1006-1355(2017)06-0173-07

2017-04-17

刘晓强(1971-)，男，黑龙江省肇源市人，高级工程师，副总工程师。主要研究方向为汽轮机监测与控制。E-mail:liuxq@shanghai-electric.com

荆建平(1969-)，男，博士，教授，博士研究生导师。主要研究方向为振动噪声分析与控制。E-mail:jianpj@sjtu.edu.cn