非均匀梁结构减振降噪吸振装置的多目标优化设计

熊夫睿，叶献辉，冯志鹏

（中国核动力研究设计院 核反应堆系统设计技术重点实验室，成都 610041）

非均匀梁结构减振降噪吸振装置的多目标优化设计

熊夫睿，叶献辉，冯志鹏

（中国核动力研究设计院 核反应堆系统设计技术重点实验室，成都 610041）

非均匀梁结构广泛存在于汽车、航空、船舶等工业领域中。开展非均匀振声分析和优化，对实现结构的整体减振降噪具有重要意义。引入一类含平动和转动自由度的吸振装置，首先建立沿轴向几何尺寸非均匀的梁结构振声分析数学模型。该数学模型中吸振装置和非均匀梁的运动方程相耦合。运用传递矩阵方法，对耦合系统进行频域内的振声响应分析，提出表征结构在频域内的振声优化指标。应用多目标粒子群算法，对耦合吸振装置的非均匀梁结构的振声指标在频域内进行多目标优化。优化变量包括吸振装置的个数、刚度参数、布置位置等。在5 Hz至800 Hz频段内对吸振装置进行多目标优化设计，实现非均匀梁结构在该频段内的减振降噪。

振动与波；非均匀梁；吸振装置；多目标优化；传递矩阵法；减振降噪

非均匀梁结构在工业中有着广泛使用。许多机械部件，如舰船的壳体、多级火箭、吊车臂等都可以通过非均匀梁进行结构动力分析的简化建模。针对非均匀梁结构的减振降噪研究十分必要。关于非均匀梁的结构动力学相关研究近年来主要包括：孙建桥通过传递矩阵的方法研究了一类非均匀梁的振声耦合响应[1]；文献[2]通过微分变换的办法研究了广义弹性支承下非均匀梁的响应问题；作为动力学问题中最核心的问题之一，动力系统的稳定性问题一直是学者关注的热点，文献[3]提出了一种基于1阶连续振动函数的非连续梁在外载荷下的稳定性判断条件；针对非均匀梁结构减振考虑的尺寸优化在文献[4]中进行了详细讨论。

为实现非均匀结构的减振降噪设计，首先需要对结构的响应进行快速精确的求解。作为一种半解析的方法，传递矩阵法在求解板、梁、壳等结构的动力学问题中有着较多应用[5]。传递矩阵法通过巧妙地应用结构已有的解析解，利用适当的组合每个子系统之间的精确解，从而以较小的计算量实现结构的动力分析，特别是模态和简谐响应分析。通过传递矩阵方法，文献[1]和文献[4]报道了几何非均匀梁结构的振声研究和减振优化。

吸振器作为一类振动控制的元器件，在低频振声控制中有着广泛的应用[6–7]。由于吸振器对振动的控制和调谐不需要外界能量供应，因此属于被动控制的范畴。吸振器的优化设计原理可简单概括为通过调节其质量和刚度参数，使之在外激励作用下发生共振，从而将外激励的能量最大化地转化为吸振器单元的机械能，进而起到对主结构的减振目的。

应用吸振装置对非均匀梁结构进行减振降噪优化和设计，特别是针对多个目标的研究，在现阶段的报道中还比较少见。本文引入一类含平动和转动自由度的吸振器，通过对吸振器的参数和安装位置进行调整，对非均匀梁结构的振声指标进行多目标优化。

1 非均匀梁-吸振器耦合动力学模型

变截面非均匀梁结构的运动方程可采用欧拉-伯努利梁模型，欧拉-伯努利梁模型适用于截面长高比较大的板梁结构，其振动方程为

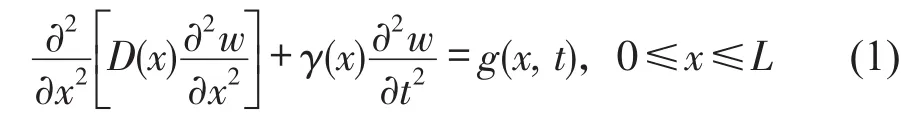
其中D(x)为沿梁轴向的刚度；γ(x)为梁轴向单位长度质量分布；g(x,t)为结构所受外载荷；w(x,t)为结构的振动位移。在求解中，非均匀梁结构的结构参数分布可认为是分段连续的，梁结构形状见图1。为运用传递矩阵方法求解结构的模态信息，可将结构的质量和刚度分布近似为

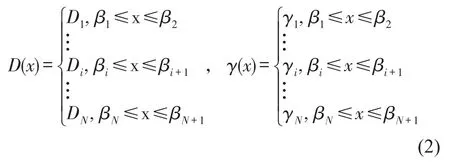
其中每段的质量和刚度分布认为是均匀的常数，则每一段结构的自由振动方程可写为

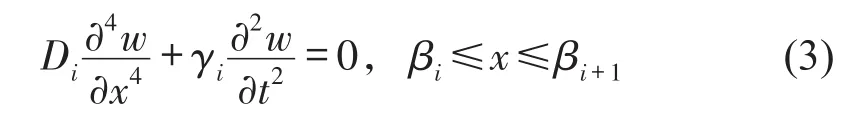
含平动和转动自由度吸振器的非均匀梁结构的示意图见图1。

图1所示的非均匀梁满足沿轴向几何参数分段连续的特性。由以上分析可写出某段含吸振器的均匀子结构的自由振动的特征方程

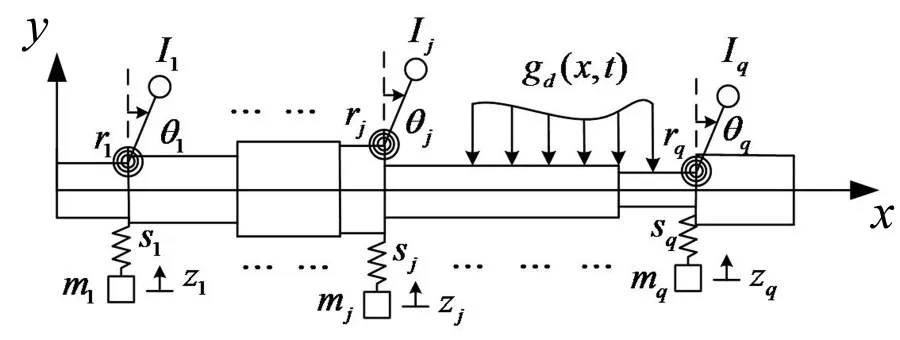
图1 含平动和转动自由度吸振器的非均匀梁结构

其中si、ri、mi、Ii为安装在x=βi+1处吸振器的平动刚度、转动刚度、质量和转动惯量。Xi为梁的振动位移的空间分布函数。式(4)中后两个方程表示吸振器在平动和转动方向的运动。吸振器平动和转动自由度的幅值可通过梁结构在吸振器安装位置的振动解来表示

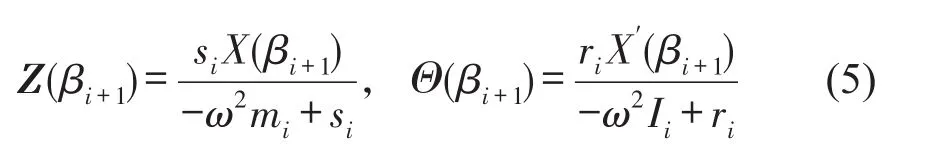
非均匀梁在吸振器安装位置的剪力和弯矩可分解为弹性结构变形的贡献和吸振器惯性力的贡献，即

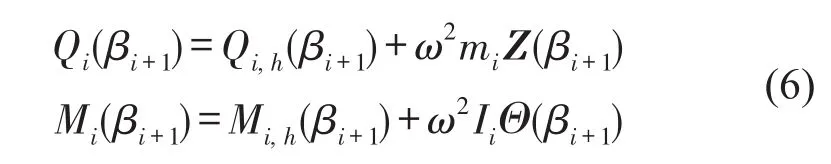
为建立每段均匀子结构之间的传递矩阵描述，引入描述均匀子结构两端振动信息的状态向量

通过整合式(4)中吸振器的运动方程，可得

由第i段梁振动而产生的从x=βi到βi+1处的振动信息传递可通过式(3)的解析解得出。式(3)的解析解为

式(11)可进一步通过矩阵方程来表示，即

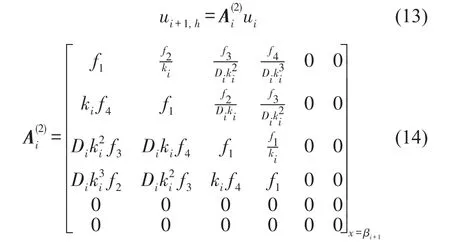
由式(8)和式(13)可推导出第i段梁在耦合吸振器后从x=βi到βi+1的传递矩阵，即

通过重复式(15)的构造过程，可将从第一段到最后一段均匀梁结构的传递矩阵表示出来。则可得到非均匀梁结构的整体传递矩阵

矩阵B是结构共振频率的函数，通过令矩阵B的元素满足响应的边界条件，可得到关于结构共振频率的代数方程，从而可求得结构的共振频率。该代数方程为超越方程，具有很强的非线性，需进行数值求解。表1给出在几种常见边界条件下，矩阵B应满足的超越方程形式。

表1 非均匀梁结构典型边界条件及频率方程

在求解出耦合系统的各阶共振频率后，结构的每阶模态可解析地表示为

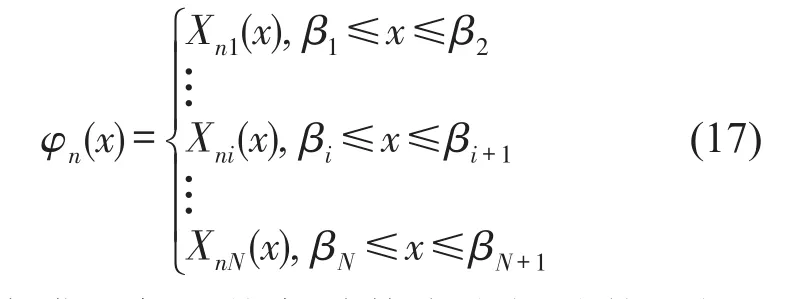
其中Xni(x)为满足每段均匀结构自由振动的通解。式(17)所示的模态函数需满足质量和刚度的归一化条件，且模态函数具有正交性[1]。

考虑吸振器惯性耦合作用的非均匀梁受迫振动方程为

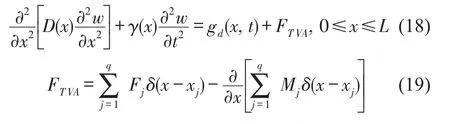
其中q个吸振器的耦合通过集中力的形式得以体现。每个吸振器的平动和转动运动方程为

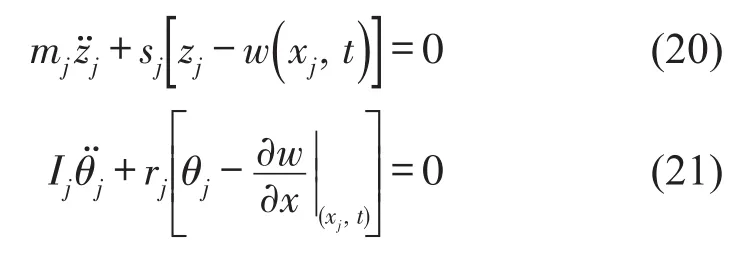
在简谐激励下，耦合系统的稳态解可写为

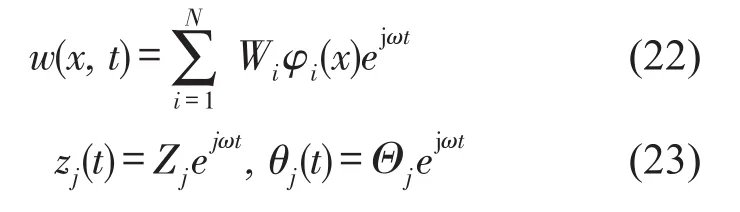
则吸振器作用在弹性结构上的力为

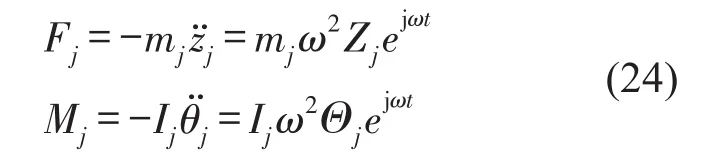
通过模态展开，并利用模态函数的正交性和归一化，可写出耦合系统关于模态坐标的矩阵方程，形式如下

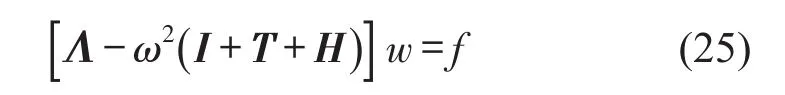
2 非均匀梁结构的声辐射

在结构简谐响应分析的基础上，本节利用简谐响应下的振动位移信息，分析结构在远场处的声辐射，为接下来的振声优化分析和设计提出优化指标。首先对模态函数进行波数变换

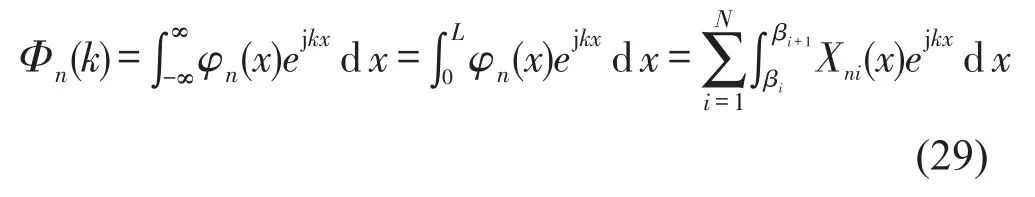
模态函数的波数变换本质上是其空间的傅里叶变换，在研究结构受迫振动下的弹性响应时，模态函数和振动速度的波数变换有着重要作用[1]。通过前节对结构在简谐响应情况下振动位移的分析，可得出其振动速度的解析解

则振动速度的波数变换为

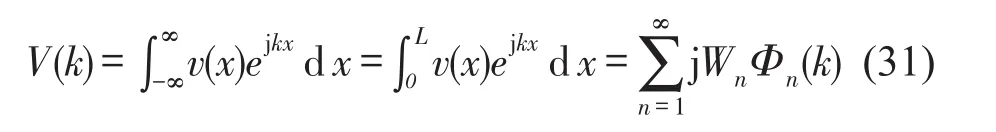
忽略结构周围声介质流体在结构上的作用力，仅考虑结构振动与流体介质的声耦合效应，可得出单位宽度结构在远场处由于结构振动而产生的辐射声能量

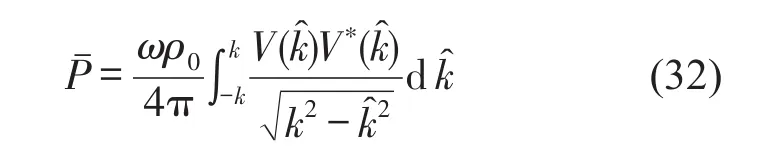
其中k=ω/c0为声波波数，c0为当地声速，ρ0为声介质密度，()*为共轭复数。在结构声学中，另一衡量结构振声信息的指标为声辐射效率，其定义为

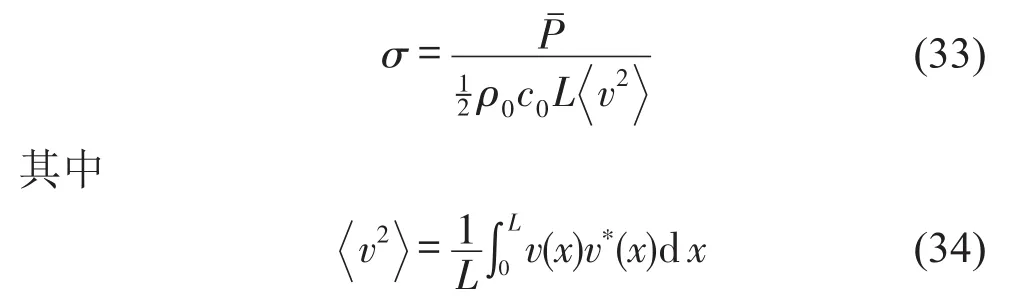
其为结构振动所产生的动能。辐射效率表征了结构在外载荷作用下振动和声辐射能量的比值，通常情况下为外激励频率的函数。在高频激励下，σ趋向于1。也就是说，高频振动的能量更容易以声辐射的形式传递出结构。在考虑结构振声优化时，通常需要降低σ来降低结构的声辐射。具体的优化思路可通过改变结构的尺寸、材料属性以及引入主被动控制等方式实现。

3 吸振装置的多目标优化设计

3.1 振声多目标优化指标和优化变量

基于前两小节提出的振声简谐响应分析，可求得耦合系统在频域内的振声信息。通过调节吸振器的参数和安装位置，可实现频域内减振降噪的多目标优化设计。定义优化参数向量

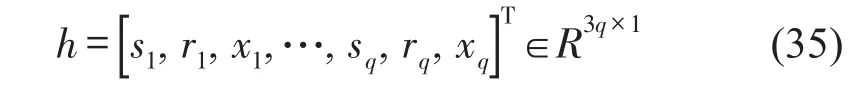
其中si、ri、xi为第i个吸振器的平动刚度、转动刚度和安装位置，q为吸振器的布置个数。

定义如下振声优化指标

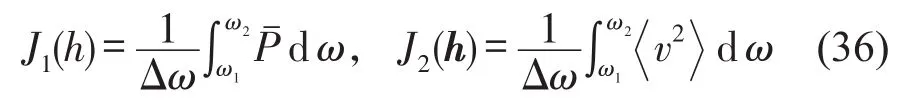
其中Δω=ω2-ω1为优化频段的带宽，为结构的辐射声能量和振动能量，其表达式分别在式(32)和式(34)给出。为避免结构静刚度过低，定义如下约束

结构的基频表征了其在静力作用下的强度，是作为结构完整性保障的一项重要指标。在式(35)定义的参数空间内，吸振器振声多目标优化问题可表达为

其中h*为满足帕累托集合定义的多目标优化解集。Q为参数空间的搜索范围。arg{}为满足优化问题定解条件的声明。min[J1，J2]表示将两个优化指标同时降低。最优解需满足式(37)所定义的约束条件。

3.2 多目标优化算法

应用多目标粒子群算法求解式(38)中定义的多目标优化问题。多目标粒子群算法(Multi-objective Particle Swarm Optimization)通过借鉴生物种群中的迁徙现象，对所提优化问题进行演化式的迭代计算求解[8]。在参数空间中，通过某一粒子的位置和速度，表征该粒子的当前状态。其优化迭代的关系满足如下方程

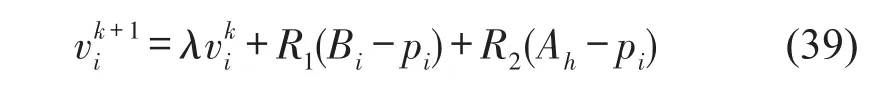
式(39)描述了种群中每一个粒子在演化过程中不断寻优的过程，通过设定种群数和迭代次数，可提高种群在参数空间中的覆盖率，进而找出更多的帕累托集合点。

为防止算法出现陷入局部极小的情况，在算法中引入变异算子，变异算子通过随机更改一定数量的粒子位置，使得每次迭代搜索的初始条件略有不同。每次迭代中能够变异的粒子占整个种群数的百分比定义如下

其中pr为变异比例，gen为当前迭代数，gmax为总迭代数。可以看出，随着迭代次数的增加，变异的比例呈指数形式衰减。这意味着变异过程主要发生在优化计算的头几次迭代，也就是当算法还不能确定帕累托集合位置的时候。优化算法的计算量和优化变量数、粒子种群大小和迭代次数有直接关系。在本文的计算中，选粒子群数目为100，迭代次数为80。

应用多目标优化算法来求解方程式(36)至式(38)中所定义的优化问题。优化变量包括减振器的刚度和安装位置，优化变量的定义见式(35)。

4 吸振装置的多目标优化结果

针对一类两边固支的非均匀梁结构，本节给出了吸振装置的优化设计方案和优化结果。研究对象的几何形式如图2所示，该结构由6个均匀子结构构成。每段均匀梁结构的截面均为矩形，截面宽度为单位宽度，截面高度从左往右分别为1.2 mm、2.3 mm、3 mm、2 mm、1.2 mm、0.8 mm。在如图2虚线所示的区间内受到均布简谐外载荷作用，载荷幅值为10 N。通过传递矩阵方法提取耦合结构的前25阶模态进行简谐响应计算。

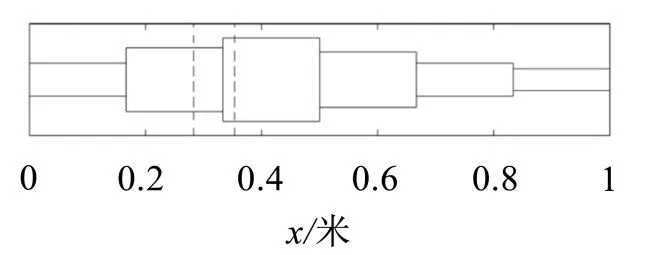
图2 非均匀结构的截面高度分布和受外载荷区域

为研究吸振器布置数量对优化结果的影响，计算了含2至5个吸振器情况下的结构频域响应。优化变量的可调范围为平动刚度从1×106N/m到9×106N/m，转动刚度从1×106N·m/rad到9×106N·m/rad，安装位置为0到1 m。表2给出了不同吸振器个数情况下优化后吸振器的参数和安装位置。

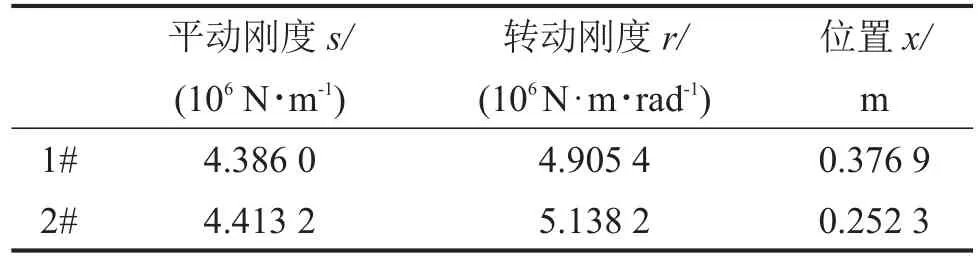
表2 2组吸振器的优化结果

表3 3组吸振器的优化结果

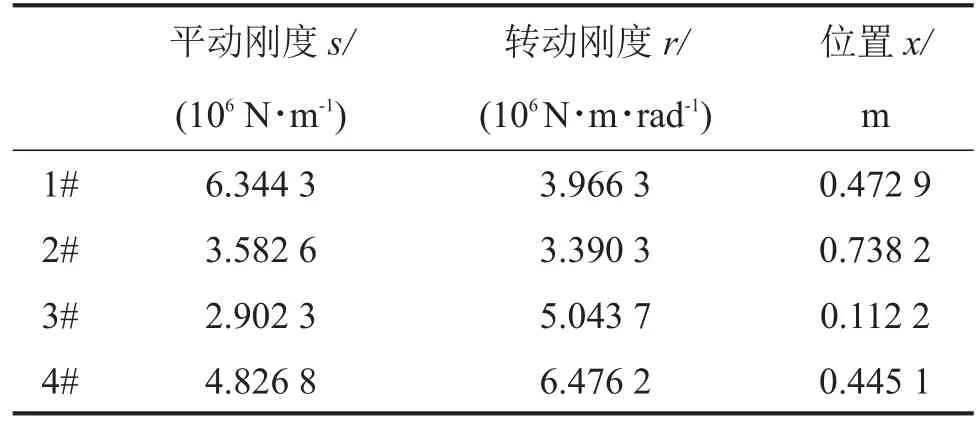
表4 4组吸振器的优化结果

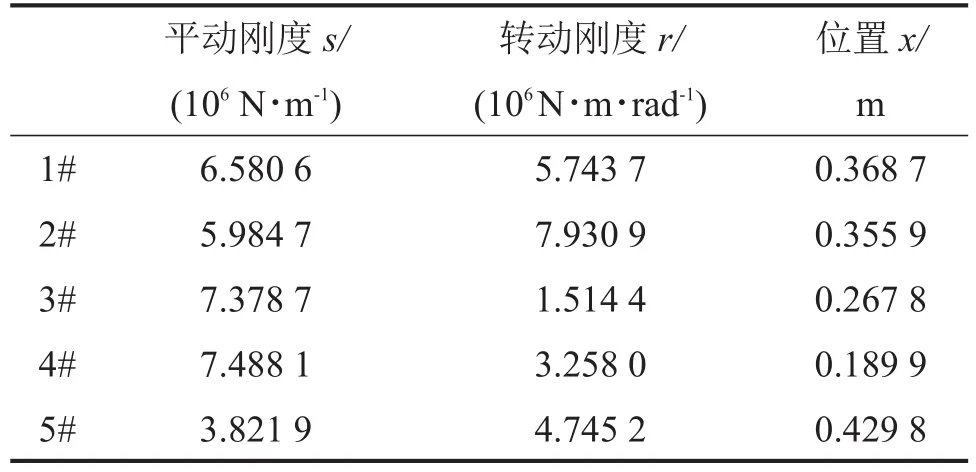
表5 5组吸振器的优化结果

通过对这些吸振器优化后的耦合系统的模态分析可以看出，吸振器的引入使得结构的模态呈现向低频处更加密集分布的趋势。针对2至5个吸振器最优布置的工况，表6给出了耦合系统前10阶的共振频率。

不同数目吸振器优化后对应的目标函数见表7。表7所示不同组数吸振器优化布置的参数分别对应表2至表5。由表7可见，对于不同数目的吸振器，根据式(36)中的优化指标来衡量，优化后的吸振器的引入均能显著降低非均匀梁结构在频域内的声辐射水平和振动能量。此外，对于不同数目的吸振装置，优化后结构的振声响应指标基本保持在相同水平。

图3至图6给出了从2组到5组吸振器优化后耦合结构在5 Hz～800 Hz频段内的声辐射功率和振动能量的响应。实线为原结构的振声频域响应，虚线为引入吸振装置后耦合系统的频域响应。可以看出，除个别共振区域外，在5 Hz～800 Hz频段内，吸振器的优化布置均能有效降低结构的振声响应。此外，吸振器的引入使得结构的模态向低频迁移，且低频处的模态密度较原结构更大。

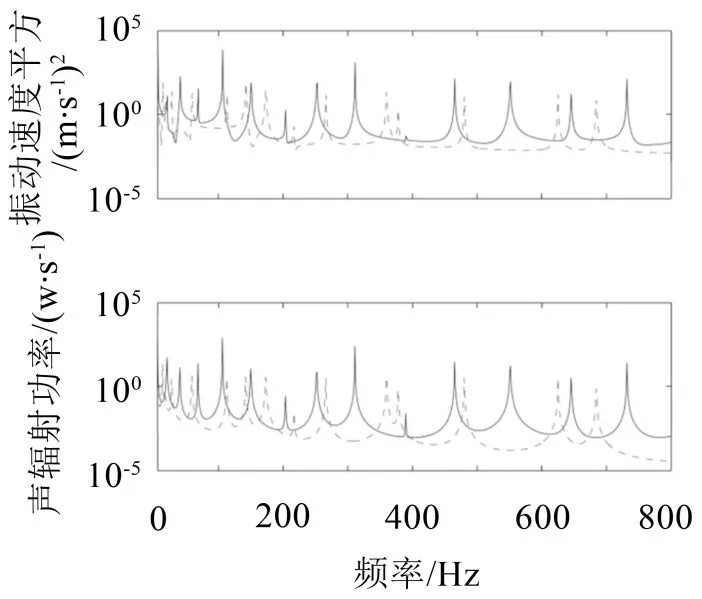
图3 最优吸振器为2组工况下耦合结构的振声响应

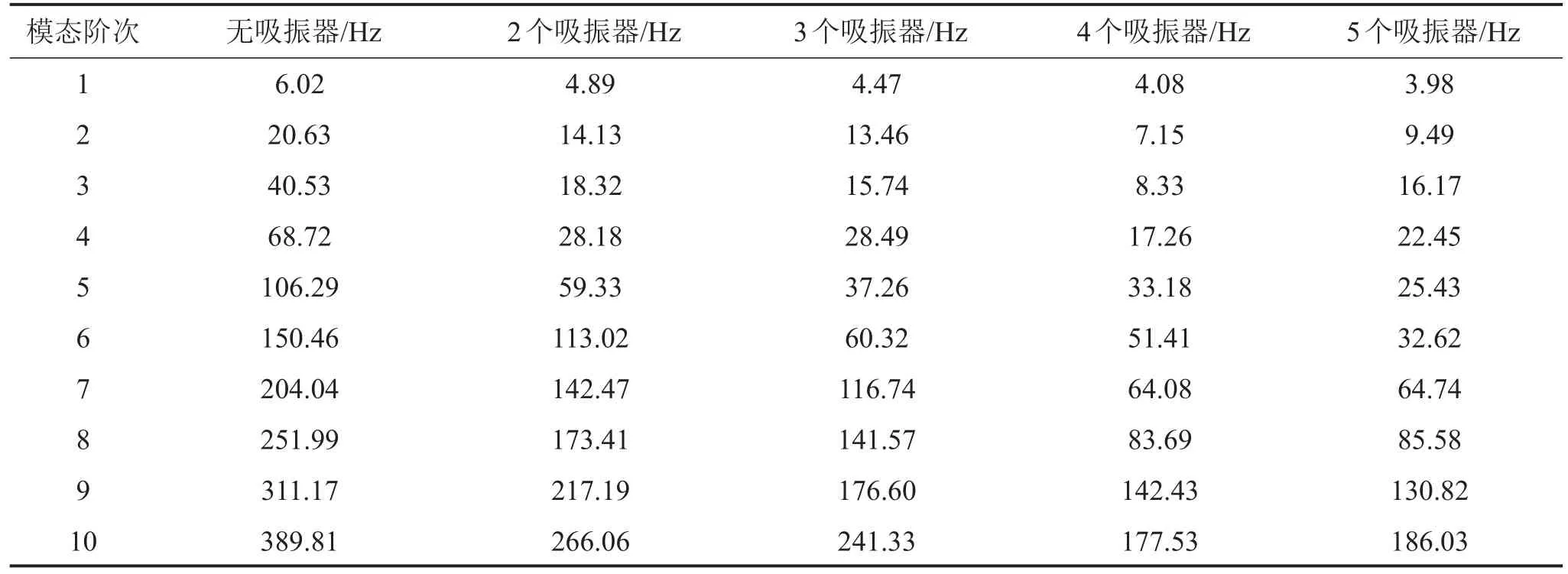
表6 不同组数吸振器工况下耦合系统前10阶共振频率分布

表7 不同吸振器组数最优设计所对应的目标函数值

图4 最优吸振器为3组工况下耦合结构的振声响应

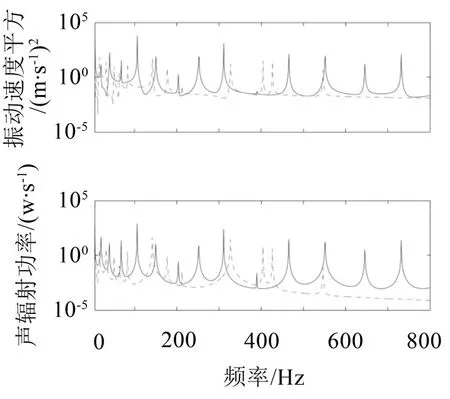
图5 最优吸振器为4组工况下耦合结构的振声响应

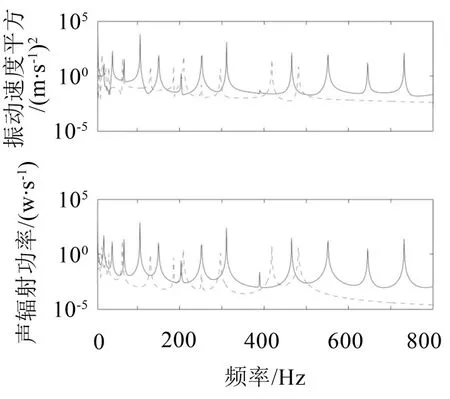
图6 最优吸振器为5组工况下耦合结构的振声响应

5 结语

本文针对非均匀梁结构的减振降噪问题，提出了一种含平动和转动自由度的吸振装置。建立了求解耦合了吸振装置的非均匀梁结构振声分析的传递矩阵模型。应用多目标粒子群算法，通过对吸振装置参数和布置位置的最优设计，对耦合系统在频域内的振声响应指标进行了多目标优化。研究表明：

（1）吸振器的引入使得非均匀梁结构的共振频率向低频段靠拢，且模态密度在低频段呈现更密集的分布；

（2）从优化结果可以看出，除共振峰处外，优化后的吸振装置可使结构在5 Hz～800 Hz频段内的振声响应在高频部分显著降低；

（3）由表7中的振声指标可以看出，不同数目吸振装置布置在优化算法的调参下，其最优布置基本保持相同的振声水平。

[1]SUN J Q.Vibration and sound radiation of non-uniform beams[J].Journal of Sound and Vibration,1995.185(5):827-843.

[2]HO S H,CHEN C K.Analysis of general elastically end restrained non-uniform beams using differential transform[J].Applied Mathematical Modelling,1998,22(4-5):219-234.

[3]AU F T K,ZHENG D Y,CHEUNG Y K.Vibration and stability of non-uniform beams with abrupt changes of cross-section by using C1 modified beam vibration functions[J].Applied Mathematical Modelling,1999,23(1):19-34.

[4]XIONG F R,HE M X.Multi-objective optimization of non-uniform beam for minimum weight and sound radiation[J].Transactions of Tianjin University,2017（1）:1-14.

[5]LU J,XIANG Y,HUANG Y,et al.Transfer matrix method for analyzing vibration and damping characteristics of rotational shell with passive constrained layer damping treatment[J].Acta Mechania Solida Sinica,2010,23(4):298-311.

[6]刘玉霞，周信，肖新标，等，列车车轮吸振器减振降噪性能研究[J].噪声与振动控制，2015，35(3)：1-4.

[7]周奇郑，王德石，李永哲.考虑振声耦合的平板结构振声特性优化研究[J].噪声与振动控制，2015，35(3)：87-91.

[8]KAVEH K D,ABTAHI A R,TAVANA M.A new multiobjective particle swarm optimization method for solving reliability redundancy allocation problems[J].Reliability Engineering and System Safety,2013,111:58-75.

Multi-objective Optimal Design of VibrationAbsorbers for Noise and Vibration Reduction of Non-uniform Beam Structures

XIONG Fu-rui,YE Xian-hui,FENG Zhi-peng
(Key Laboratory of Design Technology of Nuclear Reactor System,Nuclear Power Institute of China,Chengdu 610041,China)

Non-uniform beam structures are widely applied in the industries of auto,aerospace and ship building.So,vibro-acoustic analyses and optimizations of non-uniform beam structures are of important significance for the noise and vibration reduction of the whole structures.In this article,a type of vibration absorbers with translational and rotational DOFs is introduced.First of all,the mathematical model for vibro-acoustic dynamic analysis of the non-uniform beams with variable geometric size in the axial direction is established.In this model,kinematic equations of the vibration absorber and the nonuniform beam are coupled.Then,transfer matrix method is applied to perform the harmonic analysis of the coupled system.Structural vibration and noise radiation indices are proposed to characterize the vibro-acoustic optimization for the vibration absorbers in frequency domain.The optimization problem is solved via the multi-objective particle swarm optimization(MOPSO)algorithm.Optimization variables include the number of vibration absorbers,stiffness parameters and absorber locations.Through the optimization of the vibration absorbers in the frequency domain of 5 Hz-800 Hz,vibration and noise reduction of the non-uniform beam is realized.

vibration and wave;non-uniform beam;vibration absorber;multi-objective optimization;transfer matrix method;vibration and noise reduction

O326；O328；TB532

A

10.3969/j.issn.1006-1355.2017.06.040

1006-1355(2017)06-0199-06+215

2017-04-18

国家自然科学基金青年基金资助项目(51606180)

熊夫睿(1990-)，男，成都市人，博士，主要研究方向为非线性动力学、振动控制、多目标优化。E-mail:xfr90311@gmail.com