综合交通枢纽车致振动响应特性研究

崔聪聪,雷晓燕，张 凌

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

综合交通枢纽车致振动响应特性研究

崔聪聪,雷晓燕，张 凌

（华东交通大学 铁路环境振动与噪声教育部工程研究中心，南昌 330013）

针对“站桥合一”的大型综合交通枢纽工程，研究在不同行车速度和不同线路工况下候车厅楼板以及大跨度悬挑结构的振动响应传递规律，研究列车高速过站时站房结构的动力响应，分析客运站各个楼层的动力响应规律、车致振动在客运站内的传播衰减规律。首先，以南昌西站站房结构为例，利用无砟轨道双层梁模型对轮轨力进行数值模拟，采用有限元法建立列车-轨道-站房耦合系统整体动力学分析模型，在有限元模型上施加不同工况的列车荷载，研究结果表明正线列车所致振动响应远小于到发线列车所致振动响应，双线行车所致振动响应约为单线行车的两倍，车致振动沿着与线路垂直方向和楼层高度方向快速衰减，车致振动沿着框架柱传递振动响应，但是轴柱中心线的振动响应小于跨中的振动响应。车致振动响应沿着高度方向呈现指数衰减。车致振动响应的垂向振动、横向振动存在量级上的差异，因此综合交通枢纽车站的振动舒适度问题可以主要关注竖向振动。

振动与波；综合交通枢纽；车致振动；动力响应；衰减特性；振动水平评价

高架车站既不是单纯的房屋建筑，也不是单一的桥梁结构，而是房建与桥梁融汇在一起的一种特殊结构。按照结构体系不同，轨道交通高架车站可分为“建桥合一”和“建桥分离”两大类。综合交通枢纽的大跨度楼板结构自身的阻尼小，跨度大，大部分采用正线与站房结构分离形式。到发线由于车速低，采用“建桥合一”的形式。因此高架车站作为一种新的建筑形式，有必要对其振动特性以及舒适性进行研究。

朱志辉等以天津西站为研究对象，建立列车-轨道-站房耦合系统整体力学分析模型，考虑列车与客运站之间的动力相互作用，研究列车高速过站时列车和站房的动力响应[1]。马莉建立了车辆-无砟轨道-桥梁模型，使模型能够适用于车辆-无砟轨道-站房结构的耦合振动分析[2]。邓世海考虑了车辆与结构的耦合作用，通过动力仿真软件对新杭州东站进行数值模拟分析，求得结构的振动响应[3]。邓子铭通过将“车辆-桥梁-结构”相互作用系统分解为“车辆-桥梁”系统和“桥梁-结构”两个系统对新长沙站进行结构仿真，提取结构在列车荷载作用下的振动响应[4]。

以往的车致客运站振动响应主要关注轨道层的振动响应，而关注候车厅楼板与大跨度悬挑商业夹层楼板振动传递与衰减规律的研究很少。为此本文以南昌西站为研究背景，将用无砟轨道双层梁模型进行数值模拟得到的轮轨力加载到有限元模型上，从时域、频域方面分析不同行车速度和不同线路工况下的车致振动响应特点。

2 综合枢纽车站计算模型

南昌西站主体由下到上依次为地下层、轨道层、高架层、高架夹层。站房主体最高点距离地面41.7米，建筑外墙南北进深为385.5 m东西宽133 m，设有站台12座，其中基本站台2座；旅客到发线22条，正线4条。候车厅层位于整个站房结构地上二层，标高约8.5 m，通过伸缩缝将南昌西站候车厅楼板划分为三个区域,南昌西站东西方向柱网尺寸为18 m+18 m+18 m+25 m+18 m+18 m+18，南北为22 m+30 m+51.5 m+53 m+42 m+42 m+53 m+51.5 m+30 m+22 m。具体有限元图见图1。

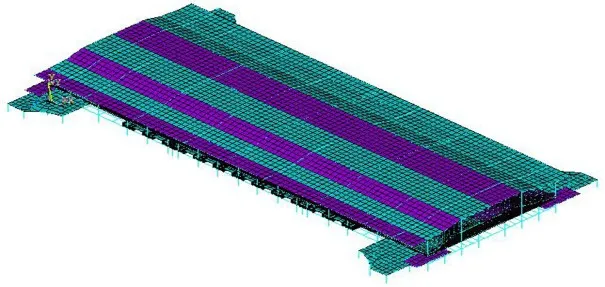
图1 南昌西站有限元模型

3 客运站结构的动力特性分析

3.1 有限元模型的建立

南昌西站综合交通枢纽站房有限元模型中钢轨用空间梁单元BEAM188模拟；钢轨扣件和轨道板支座采用弹簧阻尼单元COMBIN14模拟；轨道梁采用实体单元SOLID45模拟；上部结构中的梁、柱和杆件采用BEAM181单元进行模拟，各层楼板采用SHELL163单元模拟。

3.2 确定性列车荷载作用下结构振动响应分析

无砟轨道连续弹性双层梁模型的振动微分方程为[5]

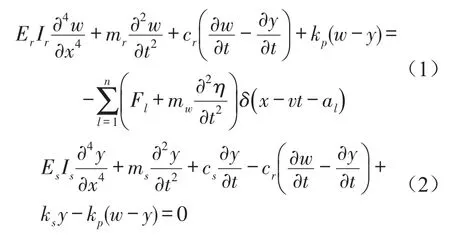
其中Er、Ir为钢轨弹性模量和水平惯性矩；w(x,t)为钢轨竖向挠度；Es、Is为轨道板弹性模量和水平惯性矩；y(x,t)为轨道板竖向挠度；mr为单位长度钢轨质量，ms为单位长度轨道板质量；cr为轨下垫板和扣件阻尼；kr为轨下垫板和扣件刚度；cs为轨道板下基础阻尼；ks为轨道板下基础刚度；δ为Dirac函数，v为列车运行速度，Fl为第l个轴重，Mw为第l个车轮质量，al为t=0时第l个轮对距原点的距离，n为轮对总数，为轨道随机不平顺值。

轨道结构双层梁模型见图2。

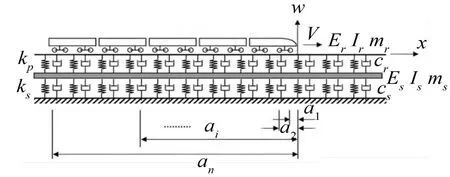
图2 轨道结构连续弹性双层梁模型

傅里叶变换后容易求得钢轨的位移、速度、加速度以及轮轨作用力，具体见图3。

从钢轨的位移、速度、加速度时程曲线中均能辨别出列车行走的痕迹。在量级上与多数的文献结果相符，说明加载与计算方法均具有可靠性。

利用无砟轨道双层梁模型对轮轨力进行数值模拟，车轮动压力数值模拟见图3（d）。

因为本文主要关注大跨度楼板、大跨度悬挑结构的振动衰减规律，因此主要研究竖向加速度响应。具体线路布置图见图4。线路1、2、3、4、5、7各表示一条到发线，线路6表示两条正线。

工况一：到发线运行工况为列车在线路1以60 km/h、120 km/h、180 km/h、240 km/h的不同速度通过枢纽车站。正线列车运行工况为列车在线路6中的一条线路以180 km/h、200 km/h、240 km/h、300 km/h的不同速度通过枢纽车站。

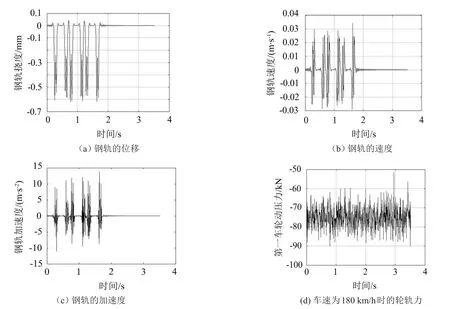
图3 钢轨各响应参数时程曲线

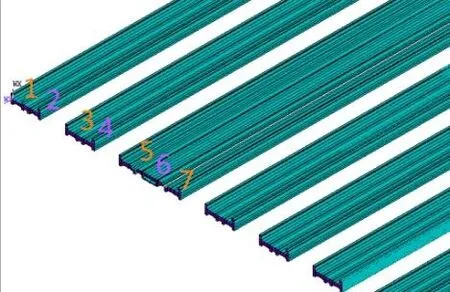
图4 具体线路布置图

工况二：列车在到发线线路1以240 km/h的车速通过枢纽车站。列车在到发线线路1、2同时以240 km/h的车速通过枢纽车站。

工况三：正线上列车在线路6中的一条线路以300 km/h的车速通过枢纽车站、正线上列车在线路6中的两条线路以300 km/h的车速通过枢纽车站。

工况四：两条正线上列车在线路6以300 km/h的车速通过枢纽车站以及相邻两条到发线上列车在线路5、7同时以240 km/h的车速匀速通过车站。

工况五：所有正线上列车以300 km/h的车速通过枢纽车站，正线两边到发线上列车以240 km/h的车速匀速通过枢纽车站。

工况六：所有到发线上列车以240 km/h的车速通过枢纽结构，所有正线上列车以300km/h的速度通过枢纽车站。

工况七：不相邻到发线上双线行车，即线路2、4上的列车以240 km/h的车速通过枢纽车站。

工况八：相邻到发线上的双线行车，即线路2、3上列车以240 km/h的车速通过枢纽车站。

以下所有的数据表中的数据单位均为cm∕s2。

工况介绍：如图5所示为建立的有限元模型剖面图。

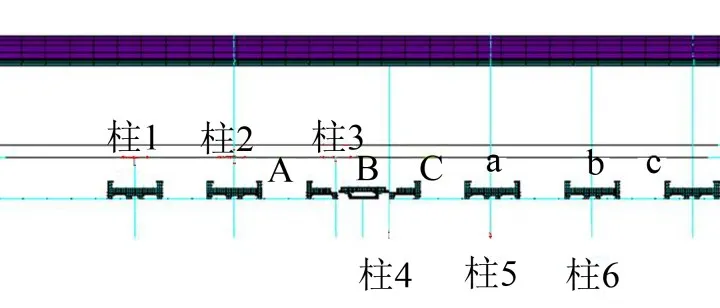
图5 模型的剖面图

柱1、2、3、4、5、6为框架柱，因为轮轨力通过框架柱传递振动响应，因此本文所指的距正线距离是指到柱4的距离，所指的到发线距离均是指到柱1的距离。

点A、B、C为楼板处到到发线（框架柱1）距离为24 m、48 m、60 m的点，a、b、d为楼板处到正线（框架柱4）距离为24 m、48 m、60 m的点。

工况四、工况五、工况六、工况七、工况八中关键点振动响应介绍：到发线关键点1位于柱1正上方的跨中楼板处，关键点2位于柱1正上方的大跨度商业夹层处，关键点3位于柱4正上方的跨中楼板处，关键点4位于柱4正上方的大跨度商业夹层处。

3.2.1 不同列车行驶工况下振动衰减规律

表2为到发线列车在不同行驶速度工况下不同结构层的响应。正线列车通过综合交通枢纽车站时在不同行驶速度工况下不同结构层的响应见表3。正线列车、到发线列车在单双线行车时不同结构层的响应见表4。

表2 不同行驶速度下的响应/(cm·s-1)

表3 不同行驶速度下的响应/(cm·s-1)

从以上分析可以看出：对于正线轨道而言，轨道上没有竖向支撑与上部结构相连接，振动响应不能直接传至上部结构，只能通过站台梁传到两侧轨道再通过两侧轨道的竖向支撑传至上部结构，这种传递方式导致列车在正线上运行时楼板上方振动响应小。列车的振动响应沿着高度的方向迅速衰减。

双线行车工况下大跨度商业夹层与候车厅层楼板竖向加速度差不多为单线行车工况下的两倍，正线上列车即使双线行驶，运行时传递给上部结构的振动响应也偏小。不同工况下正线、到发线关键点的振动响应见表5。

通过上述表格可以看出：工况四与工况五说明四条正线、四条到发线上列车同时运行与两条正线、两条到发线列车同时运行竖向加速度差别不大，工况五竖向响应最大值并不是工况四的两倍，因为两条轨道相距较远，激励叠加程度较小，所以竖向响应有所增加但程度不大。工况七表明相离线路同时行车时的响应并不是单独线路行车时的两倍，说明相离线路之间的影响不大，工况八说明相邻线路行车影响较大。

工况六为全部线路行车时的工况，是对楼板响应最不利的工况。用此工况下的振动响应可以进行舒适度评价。

为了充分分析综合交通枢纽振动激励的传播和形成机制，分析综合交通枢纽结构局部振动特性、频谱响应、共振机理及影响因素。需要综合选取不同楼板跨度，不同结构层的关键点进行分析。

表4 单双线行车时的响应/(cm·s-2)

表5 正线、到发线的关键点振动响应/(cm·s-2)

3.2.2 不同楼板跨度工况下楼板中央的振动衰减规律

当到发线上列车、正线上列车匀速通过枢纽结构时不同跨度楼板的振动响应见表6。

将振动响应用图6、图7直观表示如下。

图6 距到发线距离不同时的振动响应

通过以上分析可以看出，对于不同跨度的楼板，楼板中央的振动衰减规律一致。

无论是正线上行车还是到发线上行车，25 m大跨度楼板的振动响应比18 m大跨度楼板的振动响应大。

3.2.3 列车在到发线上以及正线上通过枢纽车站时不同轴柱中心线处的振动响应规律

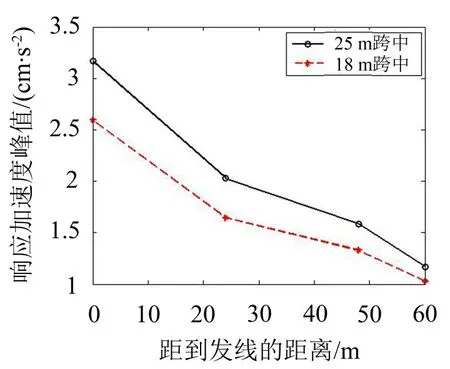
图7 距正线距离不同时的振动响应

当列车在到发线上、正线上以匀速通过枢纽结构时不同轴柱中心线处的振动响应见表7，将振动响应用图7直观表示。

通过以上分析可以看出到发线上列车通过时以及正线上列车通过时，通过轴柱中心线传递的振动响应。

但是通过与表2中到发线上列车以180 km/h的速度通过时楼板的振动响应对比，可以看出轴柱中心线处的振动响应小于跨中的振动响应。

3.2.4 不同结构层的振动衰减

选取综合交通枢纽车站有限元模型屋顶层顺轨中部关键点，选取靠近线路的站台中部关键点进行分析。所选取的关键点在水平方向差距不大，用于研究振动在竖直方向的衰减规律。

当到发线上列车以180 km/h的速度通过枢纽车站时各结构层关键点在横向、竖向的振动响应见表8。衰减图见图8。

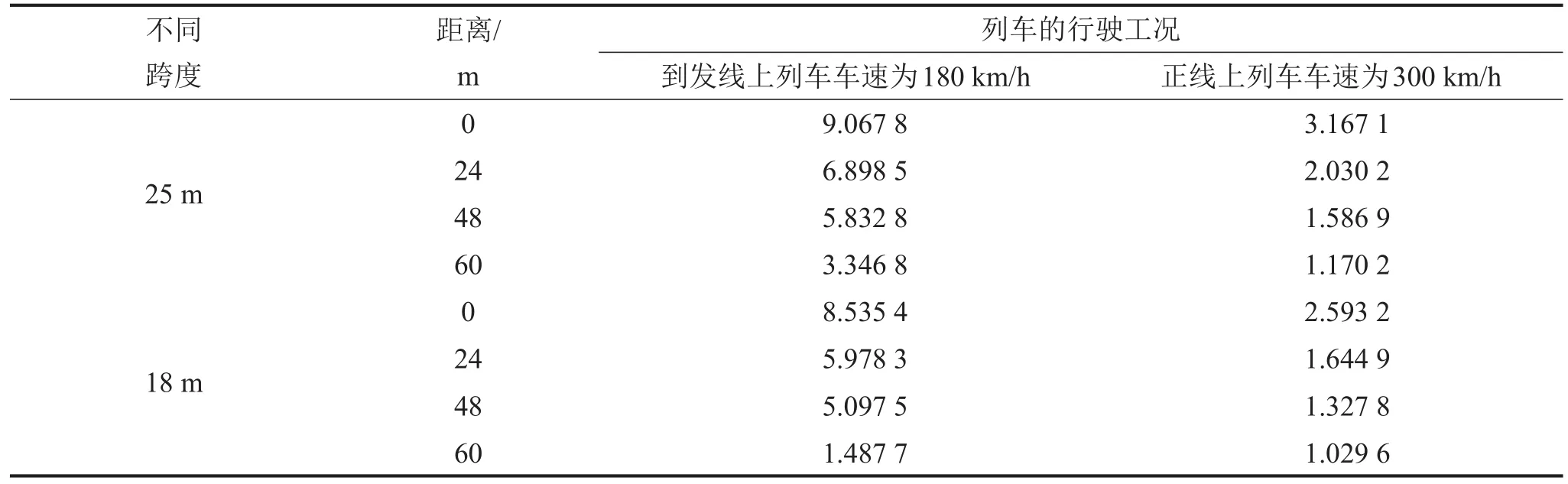
表6 不同跨度工况下枢纽结构的振动响应/(cm·s-2)

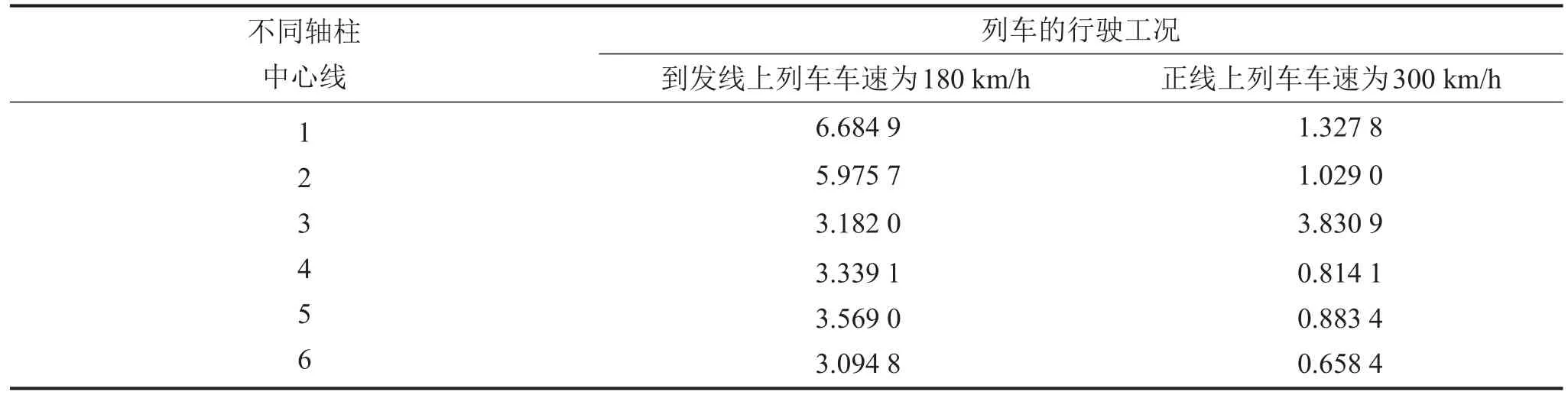
表7 不同轴柱中心线处的振动响应/(cm·s-2)

表8 不同结构层的响应/(cm·s-2)

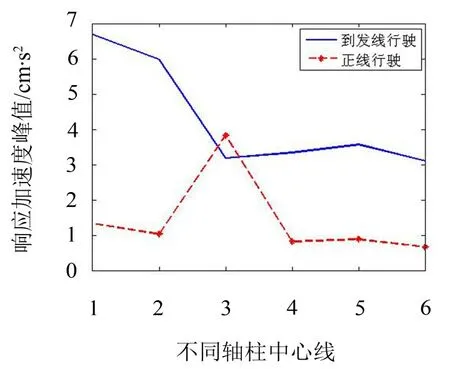
图8 不同轴柱中心线的振动响应

通过枢纽车站各结构层关键点在横向、竖向的振动响应可以看出横向振动响应远小于竖向振动响应，沿着高度的方向车致振动呈现指数衰减，见图9。

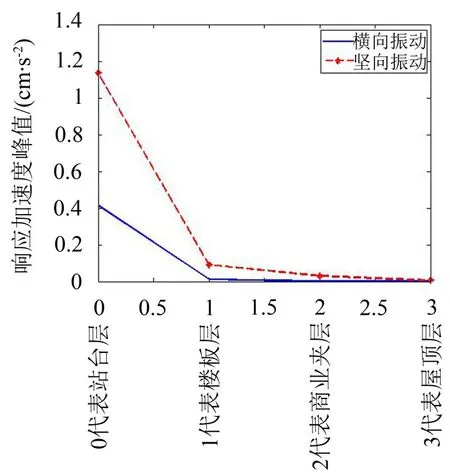
图9 关键点沿着高度的方向振动衰减规律

4 振动水平评价

4.1 时域分析

选取典型荷载工况下的楼板关键点，直观分析楼板的垂向振动与横向振动响应见图10。同一结构层不用距离处的时域加速度响应见图11。

通过典型荷载工况的时域分析可以直观地看出关键点在竖向的振动响应与横向振动响应存在量级上的差距，振动响应随着距离的增大迅速衰减。

图10 不同方向的振动响应

图11 不同距离的振动响应

4.2 频谱分析

为了分析候车厅楼板的振动特性，选取到发线上列车以行驶速度240 km/h、正线上列车以行驶速度240 km/h、正线上列车以行驶速度300 km/h单(用红线表示)、双（用蓝线表示）线通行综合枢纽车站时，楼板层与相应的大跨度悬挑商业夹层典型频谱图进行分析，见图12。

通过频谱分析可以看出无论是正线上列车还是到发线上列车引起的振动传至候车厅楼板与商业夹层的频谱主要以1到20 Hz的低频振动为主。到发线上行车引起的振动幅值远大于正线上行车引起的振动幅值，双线行车作致振动的幅值为单线行车的两倍。车致振动幅值沿着高度的方向迅速衰减。

4.3 振动水平评价

为了分析列车通过时楼板振动水平在频域上的分布，对振动响应信号进行1/3倍频程分析，得到振级频谱曲线。

典型工况下关键点的振级频谱曲线，以到发线上列车以车速240 km/h单线行驶时楼板层、大跨度悬挑商业夹层为例，垂向加速度振级频谱图见图13、图14。

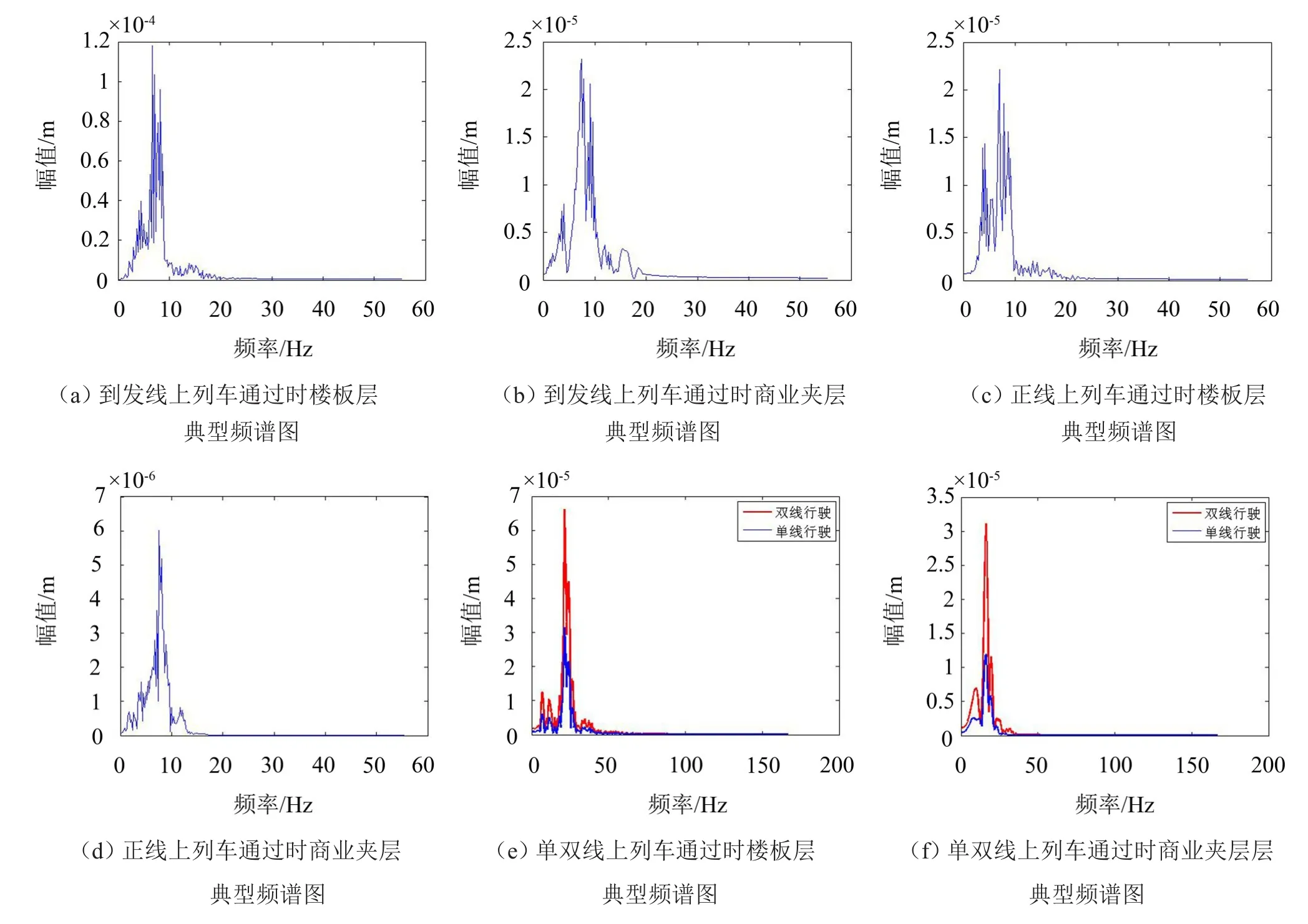
图12 楼板层与商业夹层典型频谱图

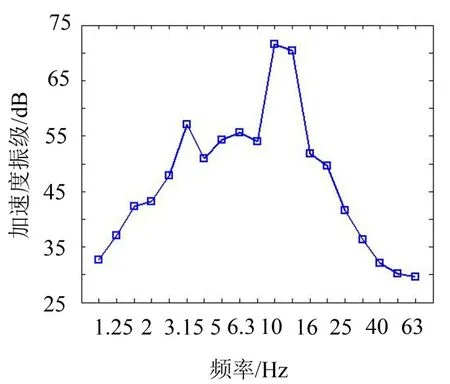
图13 楼板层垂向加速度振级频谱图

图14 商业夹层垂向加速度振级频谱图

通过振级频谱曲线可以看出，楼板在频率为3 Hz处竖向振动加速度振级出现第一次峰值。而大跨度商业夹层在频率为2 Hz处竖向振动加速度振级出现第一次峰值。大跨度商业夹层比楼板层较早出现振级峰值，其最大的垂向加速度振级分别为72 dB和56 dB，说明车致振动在垂直方向迅速衰减，与前面的研究吻合。

5 结语

（1）对于正线轨道而言，轨道上没有竖向支撑与上部结构相连接，导致列车运行时楼板上方振动响应小。列车的振动响应沿着高度的方向迅速衰减。双线行车所致振动响应差不多为单线行车时的两倍，四条正线上同时双线行车时的竖向响应最大值并不是两条正线上双线行车时的两倍，因为两条轨道相距较远，激励叠加程度较小，所以竖向响应有所增加但增加程度不大。

（2）相离线路上同时行车时振动响应并不是单独线路上行车时的两倍，相离线路之间的影响不大，相邻线路上行车影响较大。

（3）不同楼板跨度工况下中央楼板的振动衰减规律一致，25 m大跨度楼板的振动响应比18 m大跨度楼板的振动响应大。

（4）到发线上列车以及正线上列车均通过轴柱中心线传递振动响应，但是楼板中央的振动响应较轴柱中心线的振动响应大。

（5）枢纽车站各结构层关键点横向振动响应远小于竖向振动响应。沿着高度的方向车致振动振动呈现指数衰减。

（6）列车传至候车厅楼板与大跨度商业夹层的振动以0～20 Hz的低频振动为主。

（7）大跨度商业夹层比楼板层较早出现振级峰值，峰值频率接近人行荷载的频率，人致振动舒适度问题应该得到重视。

[1]朱志辉，官斌，余志武，等.列车-“站桥合一”大型客运站耦合振动响应分析[J]中国铁道科学，2014，35（5）：38-46.

[2]马莉，王澜.客运专线高架车站的减振设计研究[J].铁道建筑，2011(8)：15-18.

[3]邓世海，郭向荣，土慧慧，等.高速列车对建筑结构的振动影响[J].噪声与振动控制，2010，30(2)：72-76.

[4]邓子铭.新长沙站结构振动分析与振动控制研究[D].长沙：中南大学，2010.

[5]雷晓燕，仲志武.高速铁路无砟轨道振动分析[J].铁道工程学报，2009，1(124)：36-40.

Study on Vehicle-induced Vibration Response Characteristics of an Integrated Traffic Hub

CUI Cong-cong,LEI Xiao-yan,ZHANG Ling
(Engineering Research Center of Railway Environment Virbration and Noise,Ministry of Education,East China Jiaotong University,Nanchang 330013,China)

With the“station and bridge”large-scale integrated traffic hub as the project,the vibration response and vibration transmission law of the waiting floor and the large span cantilever structure under different train’s speed and different track conditions are studied.The dynamic response of the structure of the station,when the trains are passing by at high speeds,is studied.The dynamic response of each floor of the passenger station is analyzed.And the law of propagation and decay of the vehicle vibration in the passenger station is discussed.With the station structure of Nanchang West Station as an example,the numerical simulation of the wheel-rail force is carried out by using the double-layer beam model of ballastless track.The finite element method is used to establish the whole dynamic analysis model of the train-track-station coupling system.The results show that the vibration response induced by the positive trains is much smaller than that induced by the arrival trains;the vibration response of the double-lane traffic is nearly twice that of the single-lane;and the vibration induced by vehicles decays rapidly in the transverse direction and upward direction of the track.The vehicle induced vibration propagates along the frame column,but the vibration response in the shaft central line is smaller than that in the middle of the span.The vehicle-induced vibration decays exponentially in the upward direction.The vehicle-induced vertical vibration is much larger than the lateral vibration.Therefore,the problem of ride comfort improvement of the integrated traffic hub can focus on the vertical vibration.

vibration and wave;integrated transportation hub;vehicle induced vibration;dynamic response;attenuation characteristics;vibration level evaluation

O422.6

A

10.3969/j.issn.1006-1355.2017.06.030

1006-1355(2017)06-0144-07+172

2017-04-11

国家自然科学基金资助项目(51478184)

崔聪聪(1991-),女，山东省莱阳市人，硕士研究生，从事铁路环境振动与噪声研究。E-mail:18353121945@163.com

雷晓燕（1956-），男，江西省丰城市人，教授，博士，从事铁路环境振动与噪声研究。E-mail:xiaoyanlei2013@163.com