输电塔动力特性计算与模态试验研究

陈守海，谭 平，杨子玄

（东南大学 火电机组振动国家工程研究中心，南京 210096）

输电塔动力特性计算与模态试验研究

陈守海，谭 平，杨子玄

（东南大学 火电机组振动国家工程研究中心，南京 210096）

输电塔是国家电网的重要组成部分，具有结构高、跨度大、柔性强等特点，对风荷载反应灵敏。建立能反映输电塔动态特性的模型对风致振动控制至关重要。为研究输电塔理论模型的准确程度，分别建立3种输电塔实验模型，包括多质点模型、梁单元有限元模型和梁-杆混合单元有限元模型，并对其进行模态分析；同时采用锤击法，以单点激励多点响应（SIMO）的测试方法对输电塔实验模型进行模态测试。将各方案与测试结果进行比较分析，结果表明：梁-杆混合模型的求解精度高于另外两种计算模型的精度，能较好模拟输电塔的动力特性，是最优的输电塔模拟方案。

振动与波；输电塔；串联多质点模型；有限元模型；动力特性；试验模态

近年来，随着高压输电塔高度的增加，风损和风毁事故在世界各地频繁发生。研究输电塔风致动力特性并开展减振抑制技术研究已越来越重要。调谐质量阻尼器（TMD）具有结构简单、效果显著、造价低的特点，在大型结构体减振领域得到广泛应用。研究结果表明，结构体固有频率准确与否对TMD减振效果的影响很大。固有频率偏差5%，减振效果降低20%[1]。输电塔动力特性可以通过计算或实测的方法获取，在设计阶段，主要还是依赖于计算分析。因此，计算分析模型的准确性对于TMD减振设计至关重要。

输电塔常用的计算分析模型有：多质点模型[2–4]、梁单元模型[5–7]、梁-杆混合模型[8–9]。多质点力学模型将结构简化为多个集中质量单元串联而成的多自由度系统，它减少了结构的自由度数，计算量小，能够很快得到结构的内力和变形[10]。该模型计算效率高，主要用于输电塔线体系风振响应分析，但它计算不够精确，无法体现局部模态。梁单元模型和梁-杆混合模型均是有限元模型。梁单元模型是将所有杆件均用梁单元模拟，它同时考虑弯矩和轴力作用，求解结果较准确，适用于线性、大角度转动和非线性大应变等场合。但是结构刚度较难确定，模型存在整体刚度偏大的问题[11]。梁-杆混合模型是根据结构受力不同，将主材（横膈材、斜材）用梁单元模拟，辅材（次腹杆）用杆单元进行模拟。该模型能合理地降低模型的整体刚度，计算精度较高，同时也存在过程繁琐、工作量大的问题。这三种模型都有各自的优缺点和适用范围，在工程中都得到了广泛应用。

本文建立输电塔3种计算分析模型，将三种模型求解结果与试验模态分析结果比对，分析比较这3种模型在输电塔动力特性计算分析时的准确度。

1 模态分析方法

1.1 计算模态分析

结构受力作用时，其动力学方程为

式中M、C、K分别为结构的质量、阻尼、刚度矩阵，通常为n阶实对称矩阵分別为结构相对于地面的加速度、速度、位移列向量为结构所受外力向量。忽略阻尼，输电塔可以视为n个自由度无阻尼自由振动系统，方程为

该方程是常系数齐次微分方程组，特征方程为

其中A=（Aj）(j=1,2…,n)，是各个坐标振幅组成的n阶列阵。A具有非零解的充分必要条件是系数行列式等于零。

解此方程便可得到结构的固有频率。每个固有频率ωi对应于各自的本征向量A（i），满足

将求得的固有频率代入式（5）可得系统各阶主振型ϕ（i）。

1.2 试验模态分析

假设系统初始状态为零，对式（1）两边进行拉普拉斯变换，得到以复数s为变量的方程式

将s=jω代入上式，可得到系统在频域中输出响应和输入响应之间的关系式

其中H(ω)是实对称矩阵，对其进行相应的变换和推导可得

式中Ak表示第k阶留数；Pk为第k阶极点。上式分子、分母中分别含有模态振型信息和频率、阻尼信息。通过试验获得频响函数后，通过模态参数识别技术可以得到系统全部模态信息。

2 输电塔动力特性计算分析模型

以某酒杯型输电塔模型为例开展研究。塔高1.8 m，塔头宽度为0.80 m，根开0.40 m，塔体总质量为18.2 kg。该塔是由角钢与扁钢组合而成，主体横截面为正方形，无爬梯等附属结构，材料之间采用焊接。塔底部与地面之间采用钢钉固定。整体结构如图1所示。

图1 输电塔模型

2.1 多质点模型

多质点模型是基于集中质量法的一种简化求解方法，它将连续分布的质量集中在系统内的某些点上，各质量之间采用无质量的弹性连接[12]。简化模型是含有限个集中质量的多自由度系统，在对其进行模态分析时，只需将系统的质量矩阵M和刚度矩阵K代入式（2）便可。

2.1.1 简化模型的质量矩阵

由于塔架所受的外力主要是横向风载荷，塔架的每层横杆、横膈的平面内刚度比较大，在水平风载荷作用下，同一层塔架各节点之间的水平位移差值相对于它们的水平位移值都很小，所以可以将塔的一层视为一个质点[13]。质点位置宜选在平面刚度较大且质量聚集处。

根据塔的结构特点，将塔分为6层，每一层塔柱、横杆、斜杆质量集中到相应层上，质量集中在横杆处。图2为简化后的模型。

图2 输电塔多质点模型

由文献[12]可知，该模型的质量矩阵是一个对角矩阵，对角元素依次为各个质点的质量。质量矩阵为

各质点质量可用Ansys软件获得，相关数据见表1。

表1 简化模型参数

2.1.2 简化模型的刚度矩阵

在求解水平刚度矩阵[K]时，通常将塔架视为一个空间桁架结构，假定所有节点均为理想铰接，且在水平载荷和扭转载荷作用下，横截面不发生周边变形。具体求解方法如下：设结构分为i层，每层有j个节点。在每层节点上依次施加1/j的单位力，利用有限元软件求出各个节点两个方向上的位移uij和vij，取各节点位移的算术平均值作为该层集中质量的位移[14]。

节点位移向量记为

节段位移向量为

将求得的节段位移和某一节点的位移代入上式，即可求得节段的转角θ，从而得到模型的整体位移柔度矩阵[F]。通过对柔度矩阵求逆，可得简化模型的刚度矩阵[K]。

2.2 梁单元模型

在建立有限元模型的过程中，进行了如下假设：

(1)输电塔的整体结构全部是由杆件组成。

(2)杆件之间的连接方式均按刚性连接处理，且节点之间的距离等于杆件的实际长度。

(3)忽略地基对塔的影响，塔的底部视为全自由度约束。

ANSYS中的Beam188单元是基于铁摩辛柯梁理论的三维线性有限应变梁单元，它考虑了剪切变形的影响，求解精度较高。用梁单元Beam188模拟输电塔杆件，建立有限元模型如图3所示。

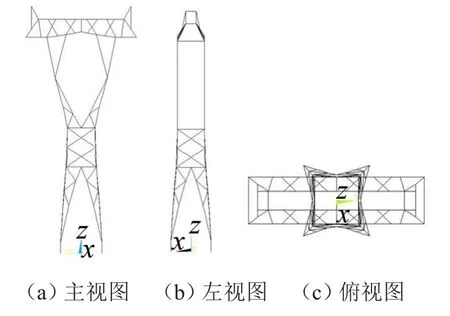
图3 输电塔有限元模型三视图

有限元模型包括7 060个节点、5 294个单元，模型总质量为18.26 kg。

2.3 梁-杆混合模型

梁单元模型是将所有的杆件均用梁单元来模拟，但是节点刚度较难确定，这会致使结构整体刚度偏大。为了更准确地模拟结构的实际刚度分布，根据结构中不同杆件的实际受力状况来确定杆件的单元类型。主材如橫膈材、斜材刚度及端部约束较大，主要承受轴力、弯矩和剪力，可用梁单元模拟；辅材如次腹杆刚度和约束较小，计算时不需要考虑自身内力，可以用杆单元模拟[9]。

Link180是一个轴向拉伸-压缩的三维杆单元，不考虑单元弯曲，该单元具有塑性、蠕变、旋转、大变形和大应变功能[15]。可以模拟辅材。

基于以上考虑，用梁单元Beam188模拟主材；用杆单元Link180模拟辅材。建立的有限元模型包括7 060个节点、5 294个单元，其中梁单元4 844个，杆单元450个。模型总质量为18.28 kg。建立的梁-杆混合有限元模型外形与梁单元模型相近，在此不再附图赘述。

3 输电塔试验模态分析

3.1 试验方法

锤击法是一种常用的模态测试方法，它覆盖频带范围宽，能激起被测系统的多阶模态，快速方便且可靠。本次测试采用锤击法中的SIMO（单点激励多点响应）法进行测量，测试系统包括：力锤、电荷放大器、加速度传感器、模态识别软件等。图4为测试系统原理图，图5为试验模态测点示意图，其中52号点为力锤激励点。

图4 测试系统原理图

图5 试验模态测点示意图

3.2 试验分析

为了减少随机误差，保证实验结果的准确性，在采集数据时对每个测点做5次测量取平均值。某测点的频响函数如图6所示。

图6 某测点的频响函数

在获得全部测点的响应数据后，通过模态识别软件，采用实模态的多项式拟合法对参数进行识别。

4 计算与试验结果比较

在工程计算分析中，通常重点考虑结构前3阶模态。现以模态测试结果为基准，3种理论模型前3阶固有频率对比见表2，振型对比见图7。

图7 振型对比

经对比得：

（1）计算与试验所得各阶模态振型相近，但三种模型计算所得固有频率相差较大。以试验结果为基准，3种模型中多质点模型最大误差为33.61%，误差最大。梁杆混合模型最大误差仅为8.12%，计算精度最高。

（2）多质点模型建模时，将各节段横截面视为刚性杆件，忽略局部变形影响，导致结构整体刚度偏大，固有频率计算结果大于真实值。此外，中心质点位移通过计算4个节点的平均值来获取，不能准确反映集中质点位移。梁单元模型全部采用梁单元模拟杆件，节点全部视为刚性节点，因而结构整体刚度偏大，结果大于实测值。

表2 不同计算模型固有频率对比

（3）梁杆混合模型合理地降低了整体刚度，误差最小。由于实验室输电塔模型根部并非完全刚性约束，因此测得固有频率会比真实值偏小，这意味着梁杆模型的实际误差会更小。

5 结语

本文以某酒杯型输电塔模型为例，建立了多质点、梁单元和梁杆混合有限元分析模型，并对其进行了计算与试验模态分析。研究发现：多质点模型计算误差最大，梁-杆混合单元模型精度最高，能较好地模拟输电塔动力特性。梁-杆混合单元模型虽然计算量大，但因其计算精度高，随着计算机技术的发展，该方法在输电塔动力特性分析领域将会得到广泛应用。

[1]陈永祁，彭程，马良喆.调谐质量阻尼器（TMD）在高层结构上应用的总结与研究[J].建筑结构，2013，43(2)：269-275.

[2]舒爱强，吴海洋，邹良浩，等.高压大跨越输电塔-线体系动力特性计算分析[J].土木工程学报，2010，43(S1)：224-229.

[3]张鹏，李宏男，宋钢兵，等.基于H_∞范数的输电塔结构动力优化[J].计算力学学报，2015，32(5)：608-612，618.

[4]瞿伟廉，殷惠君，陈波.输电线路动力分析的多质点模型研究[J].华中科技大学学报（城市科学版），2003，20(2)：1-5.

[5]汪江，杜晓峰，张会武，等.淮蚌线淮河大跨越输电塔有限元建模和修正研究[J].钢结构，2009，1(24)：21-24.

[6]李宏男，白海峰.输电塔线体系的风（雨）致振动响应与稳定性研究[J].土木工程学报，2008，41(11)：31-38.

[7]RAO N P,KNIGHT G S,LAKSHMANAN N,et al.Investigation of transmission line tower failures[J].Engineering FailureAnalysis，2010,17(5):1127-1141.

[8]邓洪洲，司瑞娟.特高压大跨越输电塔动力特性和风振响应分析[J].建筑科学与工程学报，2008，25(4)：23-30.

[9]周旸，苏桥磊.基于Ansys分析的高压输电塔结构动力特性研究[J].山西建筑，2014，40(35)：52-53.

[10]王肇民，马人乐.塔式结构[M].北京：科学出版社,2004：202-211.

[11]汪江，杜晓峰，张会武，等.大跨越输电塔有限元刚度模拟实例研究[J].特种结构，2009，26(2)：28-30，91.

[12]刘延柱，陈立群，陈文良.振动力学[M].2版.北京：高等教育出版社，2014：101-125.

[13]王肇民，PEIL U.塔桅结构[M].上海：同济大学出版社，1989：215-222.

[14]张庆华，顾明，黄鹏.格构式输电塔结构多质点简化模型研究[J].振动与冲击，2012，31(5)：148-152.

[15]刘浩.Ansys15.0有限元分析从入门到精髓[M].北京：机械工业出版社，2014：26-29.

Calculation and Modal Testing of Dynamic Characteristics of Transmission Towers

CHEN Shou-hai,TAN Ping,YANG Zi-xuan
(National Engineering Research Center of Turbogenerator Vibration,Southeast University,Nanjing 210096,China)

Transmission towers are the important parts of the state grids.They have the characteristics of high structure,large span,flexibility and sensitivity to wind loads.So,it is important to establish a model which can reflect these dynamic characteristics of the transmission towers for wind-induced vibration control.In this study,three kinds of experimental transmission tower models are established,including multi-DOF model,finite beam-element model and finite beam-rod mixed element model to testify the accuracy of the theoretical models.Modal analysis is carried out subsequently.Meanwhile,a hammering test based on Single-Input Multi-Output(SIMO)method is performed on the experimental transmission tower models.The computation results are compared with the test results.It is shown that the model using beam-rod mixed elements is the most accurate simulation model of the three.It can excellently simulate the dynamic characteristics of transmission towers.This model can be regarded as the optimal model for the transmission tower simulation.

vibration and wave;transmission tower;multi-DOF model;finite element model;dynamic characteristics;test mode

O241.82

A

10.3969/j.issn.1006-1355.2017.06.029

1006-1355(2017)06-0139-05

2017-03-29

陈守海（1993-），男，河南省信阳市人，在读硕士研究生，主要研究方向为结构振动控制。E-mail:1358722932@qq.com

谭平，男，硕士生导师，主要研究方向为机械动力学、机械振动噪声控制。E-mail:tanping@seu.edu.cn