扭力梁式后悬架模态与疲劳实验研究

黄志超，王九州，程 梁

（华东交通大学 载运工具与装备教育部重点实验室，南昌 330013）

扭力梁式后悬架模态与疲劳实验研究

黄志超，王九州，程 梁

（华东交通大学 载运工具与装备教育部重点实验室，南昌 330013）

扭力梁式后悬架是汽车行驶系统中重要的承重构件，在不同的行驶工况下，会受到不同幅值和不同频率的激励。在激励频率和扭力梁式后悬架固有频率接近或相同时，会产生共振，进而发生疲劳断裂。通过对扭力梁式后悬架进行模态实验，获得该结构的固有频率和模态振型。对同一型号的扭力梁式后悬架进行弯曲、扭转疲劳实验，得到其疲劳破坏的具体形式。对产生破坏的扭力梁式后悬架进行模态实验，对未损坏和损坏的扭力梁式后悬架各自的固有频率和模态振型进行对比分析，发现产生疲劳破损的扭力梁式后悬架在某一阶频率下的模态振型有较大变化，结构的固有频率值和固有频率分布的变化并不很大。

振动与波；扭力梁式后悬架；模态实验；疲劳实验；固有频率；模态振型

扭力梁式后悬架是汽车后悬架类型中的一种，它通过在非独立悬架上添加一根平衡杆来平衡车轮的上下跳动，保证车辆行驶平稳性，该悬架也被称为半独立悬架[1]。汽车在行驶的过程中，根据不同的行驶路况和行驶速度，扭力梁后悬架会受到不同幅值和不同频率的激励；在这些激励的作用下，扭力梁式后悬架最终会产生不同程度的结构断裂现象[2–3]，而这些轻微的破损如不能及时被发现，会对车辆带来一定的振动与噪音方面的问题。对于扭力梁式后悬架的研究，罗明军等在有限元仿真和实验结合方面进行研究[4]；范大力等针对扭力梁式后悬架的衬套刚度进行研究[5]；黄志超等通过喷丸工艺对扭力梁式后悬架进行强化，展开疲劳寿命方面的研究[6]。在模态分析理论，陈晗等针对应变模态与位移模态理论的区别进行相关研究[7]。徐浩轩主要对扭力梁式后悬架的动力特性进行了分析[8]。本文通过模态实验的方法，分别对未发生疲劳破坏和发生疲劳破坏的扭力梁式后悬架进行模态实验，对各自的固有频率和模态阵型进行对比，分析出疲劳破坏对扭力梁式后悬架固有特性的影响。

1 扭力梁式后悬架的模型

扭力梁式后悬架是汽车行驶系统中重要的承重构件，与车架、车轮和相关连接件相连，主要承载汽车后轴在各个方向传递给车架或车身的载荷。扭力梁式后悬架主要由横梁、扭杆、衬套、弹簧座、纵臂、轮毂架等结构组成，其组件的连接均是焊接。横梁截面一般有“U”或“V”形两种形状，该扭力梁式后悬架的横梁为“U”形，在横梁的内侧加装一根扭杆，加大横梁的扭转刚度。具体的三维CAD图如图1所示。各个部件的材料属性如表1所示。

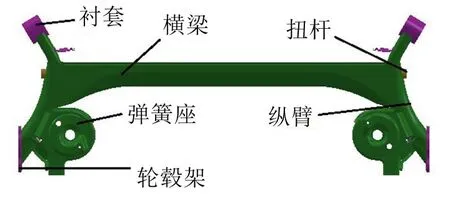
图1 扭力梁式后悬架三维CAD图

2 扭力梁式后悬架模态实验

2.1 位移模态分析理论

模态分析开始于20世纪30年代，最初用于测量飞机模态参数。经过近八十年的发展，模态分析理论已经非常成熟，包括位移模态分析技术、曲率模态分析和应变模态分析等理论。位移模态分析技术起源最早且最为成熟，其相关原理如下。

一般结构系统可以认为是一个n自由度系统，其振动方程为

对于有阻尼系统强迫振动，式（1）经过坐标变换{x}=Φ{q}得到

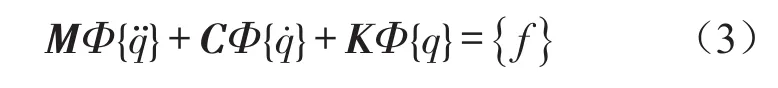
将上式两端左乘ΦT并利用正交性原理可得

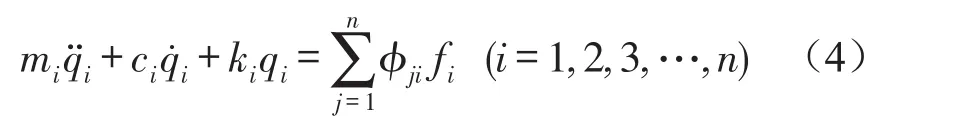
式中ci=αimi+βiki。mi称为模态质量，单位是千克，ki为模态刚度，单位是牛顿/米；ci称为模态阻尼，它的单位为千克/秒。α的单位是1/秒，β的单位是秒。

经过模态坐标变换后，比例阻尼系统自由振动方程成为

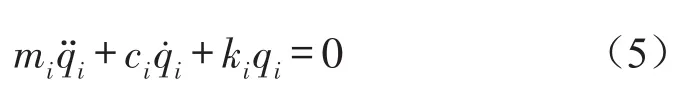
其中λi为第i阶特征值，Ωi为第i阶固有频率。

2.2 扭力梁式后悬架模态实验分析

扭力梁式后悬架的模态测试中，采用南京安正CRAS测试系统，该系统具有界面清晰、计算准确和易操作的特点，对提高整个模态实验的测试效率和测试准确性具有非常大的作用。

安正CRAS模态实验系统中，由力锤、力传感器等组成激振系统，加速度传感器、信号调理仪和数据采集器等组成数据采集系统，MaCras模态分析软件构成数据处理系统。

模态测试时需要对扭力梁式后悬架进行自由状态处理。用橡胶绳将扭力梁式后悬架对称悬挂，如图2所示。实验中的台架设施由刚性良好的材料制作；橡胶绳使用弹性良好的自行车轮胎代替，可以有效避免实验环境中的振动对模态实验的影响。

根据工程经验和CRAS测试系统使用说明可知，测试点位置的布置对于整个模态实验至关重要。如果测点布置不合理会严重影响整个模态实验的测试结果，造成人力，物力和经济上的浪费。经过大量的模态实验，总结出以下布点原则：

表1 扭力梁式后悬架相关材料参数

图2 扭力梁式后悬架悬挂方式

第一，为了能够准确反映扭力梁式后悬架的模态振型，布点轮廓要能够表现出部件的基本形状，图3为由CRAS软件建立的扭力梁式后悬架的模型，图中的数字标号即为图2中扭力梁式后悬架测试点的分布方式；

第二，在实际部件受力和易损坏部位，即关注部位，采用较大密度布置方式进行布置；

第三，对于测试部件，采用奇数布点原则，可避开测试对象的节点位置。一般一个部件的对称点处为该部件的节点，比如1/2、1/4处等。

整个模态实验采用单点激励、单点响应的测试方式，该方法具有测试思路清晰、方法简单的特点。并且由于采用单个传感器，减小了多个传感器对测试对象的影响。测试中采用力锤进行激励，用加速度传感器测量振动响应。

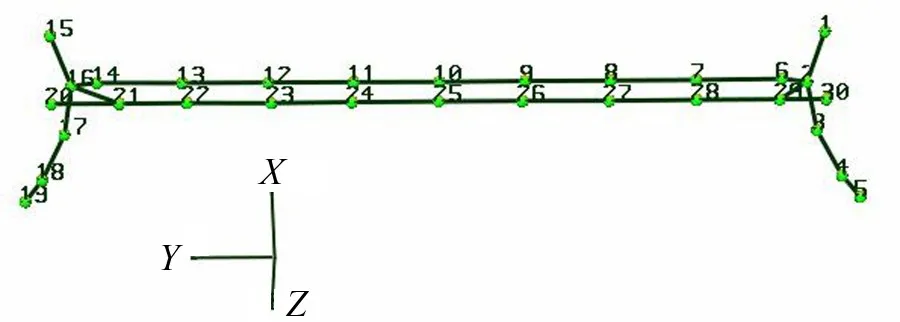
图3 扭力梁式后悬架模态实验模型

根据扭力梁式后悬架实际的运行工况，可以得知扭力梁式后悬架主要承受X、Z方向的激励，所以在模态测试过程中，分别对其X、Z方向进行测试。测试完成后通过查看模态振型正交性检验图来判别本次实验的有效性。根据线性振动系统特征值理论，任意两个特征向量应该是正交的。对于模态分析而言，任意两阶模态振型应该是正交的，即他们的矢量积应等于零。根据正交性准则可以判断扭力梁式后悬架模态实验的有效性。其固有频率和振型如图4所示。

从图4可以发现模态振型的正交性较好，证明扭力梁式后悬架模态实验测试结果是较准确的。

图4 模态正交性验证图

对扭力梁式后悬架模态实验的数据进行分析并整理，得到扭力梁0～500 Hz频段内的自由模态频率和振型，如表2所示。每1阶模态频率对应的模态振型如图5所示。

表2 扭力梁式后悬架模态实验固有频率及振型

图5 第1～7阶模态振型图

3 扭力梁式后悬架弯曲、扭转疲劳实验

汽车行驶在不平路面上，扭力梁式后悬架不仅要受到由车轮传递的纵向力，还要承受垂直方向上的交变位移载荷。因此对扭力梁式后悬架进行弯曲、扭转疲劳实验，可确定扭力梁式后悬架在承载纵向力和垂直方向交变位移载荷作用下的疲劳寿命，同时确定扭力梁式后悬架疲劳破坏的形式。

3.1 弯曲、扭转疲劳实验设备

对同规格、同型号的扭力梁式后悬架进行弯曲、扭转疲劳实验。图6、图7分别为弯曲疲劳台架实验机、扭转疲劳实验机及扭力梁式后悬架装载方式的示意图。

图6 弯曲疲劳实验机

图7 扭转疲劳实验机

施加载荷的大小按疲劳实验机公司提供的实验标准TL82431进行加载，标准TL82431如表3所示。

3.2 扭力梁式后悬架弯曲、扭转疲劳实验方案

按照扭力梁式后悬架疲劳标准TL82431对扭力梁式后悬架试样进行弯曲、扭转疲劳实验。扭力梁式后悬架的弯曲、扭转疲劳实验方案如表4所示。

在每种载荷水平条件下各进行三次台架疲劳实验。把扭力梁式后悬架安装在实验台架上后，进行弯曲、扭转疲劳实验。

3.3 实验结果以及破坏位置观察

试样进行弯曲疲劳实验后均未发生各种形式的损坏，表明扭力梁式后悬架满足弯曲疲劳实验的要求，但经扭转疲劳实验后，试样焊缝处均产生裂纹，具体实验结果如表5所示。

根据表2与表6中的结果，以及同阶模态振型图的对比，可以得出如下几点结果；

由表5中实验结果可知，该型号扭力梁式后悬架抗弯曲的能力比较强，而抗扭转的能力比较差，并且主要损坏部位为横梁与纵臂的焊缝处，说明两个不同零部件间的连接处是疲劳工况的易损处。

表3 扭力梁式后悬架疲劳标准TL82431

4 对出现疲劳破坏的扭力梁进行模态实验

采用与前面模态实验相同的测试方法，对发生疲劳破坏的扭力梁式后悬架进行自由模态实验，如图8、图9所示。通过模态实验，得到破损扭力梁式后悬架0～500 Hz内的固有频率和模态振型，见表6，各阶对应的模态振型如图10所示。

图8 破损件悬挂方式和布点

图9 扭力梁式后悬架破损位置

表4 弯曲、扭转疲劳实验方案

表5 弯曲、扭转疲劳实验结果

表6 破损的扭力梁式后悬架模态实验结果

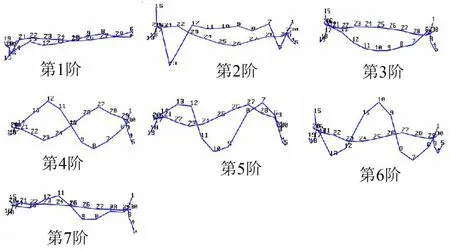
图10 第1～7阶模态振型图

根据表2与表6以及同阶模态振型图对比，可以得出如下几点结论：

(1)扭力梁式后悬架发生疲劳破坏前后的第1阶、第3阶、第5阶和第6阶的模态振型保持一致，固有频率发生小幅度的波动。

(2)扭力梁式后悬架发生疲劳破坏前后的第2阶固有频率发生小幅度的变动，但其第2阶模态振型由扭杆1阶弯曲变为扭杆和横梁均出现弯曲。经分析，扭力梁式后悬架发生疲劳破坏前后出现模态振型变化的原因是纵臂与横梁的焊接处产生疲劳破坏。

(3)扭力梁式后悬架发生疲劳破坏前后的第4阶模态振型未出现变化，但其固有频率由260 Hz变为250 Hz。而根据振动力学相关理论，结构的固有频率与结构刚度的平方根成正比例关系，可以判定第4阶固有频率的降低与焊缝的开裂有关。

(4)扭力梁式后悬架发生疲劳破坏前后的第7阶Z向的固有频率基本没变，发生疲劳破坏后的后悬架X方向的固有频率未能测到，并且第7阶的模态振型出现变化，横梁由4阶弯曲变为横梁中部2阶弯曲。

5 结语

(1)通过对扭力梁式后悬架进行模态实验分析，得到了该扭力梁式后悬架在自由状态下的固有频率和相应的模态振型。

(2)模态实验中，测点布置对于整个模态实验至关重要，为了尽可能得到更加准确的模态参数，对于对称结构，可以采用奇数布点原则，能够有效避开结构的节点对实验的影响。

(3)对扭力梁式后悬架进行疲劳实验，发现扭力梁式后悬架抵抗弯曲变形的能力较强，但是抵抗扭转变形时表现不是很好。

(4)分别对未破损和破损的扭力梁式后悬架进行模态实验，发现扭力梁式后悬架焊缝的微小损坏对扭力梁式后悬架的模态频率分布影响并不大，但对个别频率值和某些频率下的模态振型有一定影响。

[1]陈家瑞.汽车构造(下册)[M].北京：人民交通出版社，2006.

[2]何艳则.基于多体动力学的轿车扭转梁悬架运动学及NVH特性下的参数匹配优化研究[D].合肥：合肥工业大学，2009.

[3]KORONIAS GEORGE.Elastomultibody dynamics of RWD axle whine phenomena[D]. Loughborough Leicestershire:Loughborough University,2012.

[4]罗明军，宋立新，赵永玲，等.模态实验在后扭力梁上的应用[J].机械设计与制造，2013(8)：54-56.

[5]范大力，董大伟，丁渭平，等.衬套刚度对扭力梁悬架模态分布影响研究[J].噪声与振动控制，2015，35(6)：47-51.

[6]黄志超，管昌海，吕世亮，等.喷丸强化对提高汽车扭力梁疲劳寿命的研究[J].锻压技术，2016，41(4)：115-121.

[7]陈晗，宋汉文.应变模态分析及其与位移模态的关系研究[J].噪声与振动控制，2016，36(4)：7-13.

[8]徐浩轩.扭力梁悬架结构与运动特性分析[D].重庆：重庆大学，2012.

Experimental Study on Modals and Fatigue of Torsional Beam Rear Suspensions

HUANG Zhi-chao,WANG Jiu-zhou,CHENG Liang
(Key Laboratory for Conveyance and Equipment,Ministry of Education China,East China Jiaotong University,Nanchang 330013,China)

Torsional beam rear suspension is an important load-bearing component in automobile’s driving system.It is subjected to the excitations with different amplitudes and different frequencies under different driving conditions.When the excitation frequency and the natural frequency of the torsional beam rear suspension are close each other,the torsional beam rear suspension resonates,and then the fatigue fracture may occur.In this paper,through the modal test,the natural frequencies and the modal shapes of the torsional-beam structure are obtained.Then,bending and torsion fatigue tests of the torsional beams of the same type are carried out to get the specific forms of the fatigue damage.Finally,the modal experiments are carried out on the damaged torsional beam rear suspension.The natural frequencies and modal shapes of the healthy torsional beam rear suspension and the damaged one are mutually compared and analyzed.It is found that the torsional beam rear suspension with fatigue damage has a great change in the modal shapes comparing with the healthy suspension,but the frequencies and the frequency distributions of both structures are essentially the same.

vibration and wave;torsional beam rear suspension;modal test;fatigue test;natural frequency;modal shape

U463.3

A

10.3969/j.issn.1006-1355.2017.06.024

1006-1355(2017)06-0115-05

2017-05-22

国家自然科学基金资助项目(51565014)；江西省高等学校科技落地计划资助项目（KJLD13035）

黄志超（1971-），男，江西省抚州市人，博士生导师，主要研究方向为汽车后桥NVH。E-mail:hzcosu@163.com