动态保障结构下多级多层备件配置优化建模

周亮，李庆民，彭英武，李华

1.海军工程大学 舰船综合电力技术国防科技重点实验室，武汉 430033 2.海军工程大学 科研部，武汉 430033 3.海军工程大学 兵器工程系，武汉 430033

动态保障结构下多级多层备件配置优化建模

周亮1，李庆民2,*，彭英武3，李华3

1.海军工程大学 舰船综合电力技术国防科技重点实验室，武汉 430033 2.海军工程大学 科研部，武汉 430033 3.海军工程大学 兵器工程系，武汉 430033

针对作战编队执行长时间、远距离任务期间，编队后方保障站点变更的情况，结合部队维修保障的特点，基于可修复备件多级管理(METRIC)理论，通过计算编队剩余备件分布规律，建立了动态保障体系结构下基于时变可用度的三级两层备件保障模型。以备件储存空间为约束，可用度为目标，建立了分阶段边际优化模型。列举实例，采用分阶段边际算法对备件方案进行优化，对比分析了动态保障结构下和固定保障结构下装备可用度随时间的变化，并采用蒙特卡罗仿真方法对案例进行实验验证。案例结果表明：采取多个后方站点的保障方式能有效提高装备可用度；案例仿真实验结果与解析结果误差在4%以内。模型可为保障决策者制定备件方案提供辅助决策工具。

动态保障；可修复备件多级管理(METRIC)；剩余备件；分阶段；边际；蒙特卡罗仿真

备件是装备维修保障最重要的物质基础之一。作战编队是执行任务的基本作战单元，由保障单元和装备现场部署站点构成。随着战略需要，作战编队会经常性执行远距离、长时间任务。由于编队携带备件数量有限，任务期间需要后方基地站点保障，而由于编队行驶区域范围广，整个任务期间编队很难由一个固定后方基地站点进行保障，因而实行区域性就近保障，与传统固定不变的备件保障结构相比，将这种保障站点发生变更的备件保障系统称为动态保障结构系统。由于编队作战范围广，当编队由国内的后方基地站点保障时，后方基地站点不可修备件可立即向工业部门订购；当编队远离大陆本土由海外基地站点保障时，受地域条件限制，海外保障基地站点不可修备件无法及时得到补给。如飞机编队执行远距离作战任务时，在未行驶出第二岛链前，一直由国内基地保障；行驶出第二岛链后，由海外基地实施保障。

针对任务期间备件配置优化问题，国内外学者进行了一系列研究。文献[1]针对非稳态两级单层备件可修复系统提出了Dyna-METRIC模型。文献[2-3]在Dyna-METRIC模型基础上，将两级单层备件保障模型扩展成多级多层备件保障模型。文献[4-5]分别对Dyna-METRIC模型进行扩展，针对非稳态备件保障系统，建立了K/N冗余装备结构、站点维修能力有限条件下的备件配置优化模型。文献[6]对备件修复概率小于1的保障系统，将不全修复件等效为消耗件，建立了多层级不完全修复件近似可用度评估模型。文献[7]利用非平稳随机过程理论，研究并建立维修渠道数量有限条件下的备件配置优化模型。文献[8-9]针对任务期间携带备件数量受限的舰船，研究了串件拼修策略下舰船编队备件配置优化方法。文献[10-12]针对任务期间站点备件分配、管理问题，考虑备件送修分配优先级顺序，建立了备件分配与送修动态管理模型。以上研究均未考虑任务期间保障站点发生变更时的备件优化配置问题。

本文以作战编队执行远距离、长时间任务为背景，针对编队中装备部署现场站点仅具备LRU(Line Replaceable Unit)换件维修能力、保障单元站点对SRU(Shop Replaceable Unit)不可修的保障特点，采用理论建模与仿真验证相结合的手段，对编队后方保障站点发生变更情况下的备件配置优化问题进行研究。

1 问题描述及条件假设

1.1 保障过程

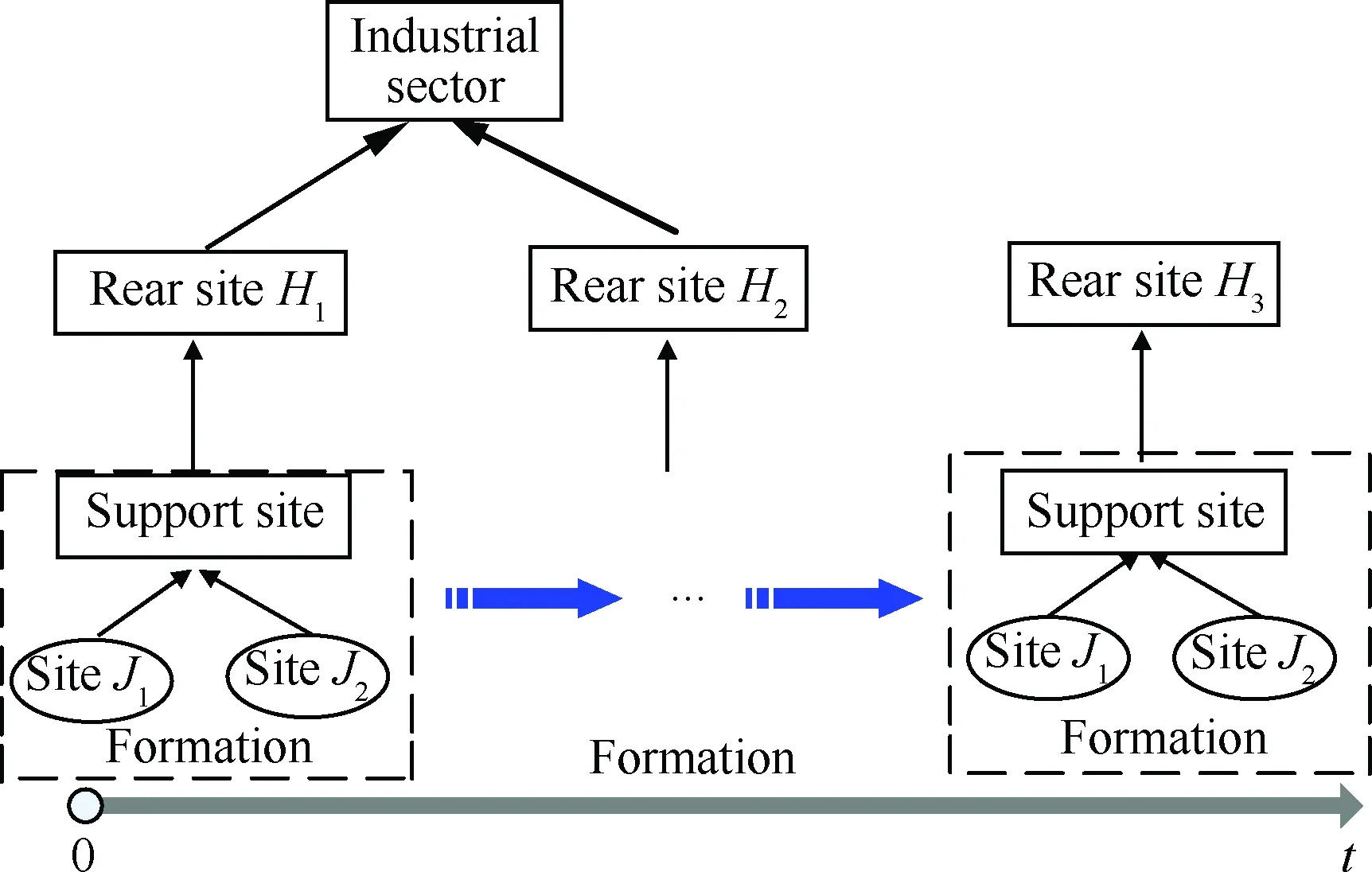
设由作战单元j和保障单元z组成的编队，依次在L1,L2,…,Ln,…,LN等区域执行任务，在L1,L2,…,Ln,…,LN等区域执行任务时对应的后方保障站点依次为H1,H2,…,Hn,…,HN，进入H2,H3,…,Hn,…,HN区域的计划时间依次为T1,T2,…,Tn-1,…,TN-1，编队由各后方站点保障的时间段如图1所示。编队在Ln区域执行任务时，一旦装备发生故障，若作战单元j在Ln-1区域执行完任务剩余备件大于0，则对装备进行换件维修，并将拆换下来的故障件送保障单元z进行修理，并向保障单元z申领备件;保障单元z判断送修备件是否可修，不可修的备件送Hn站点进行修理，同时向Hn站点申领备件;Hn站点收到送修备件后，判断备件是否可修，若可修则送修理车间修理，若不可修，则判断Hn站点属性，若Hn站点为国内站点，则不可修备件立即向工业部门订购，若为海外基地站点，则不可修备件等待任务结束后申领。

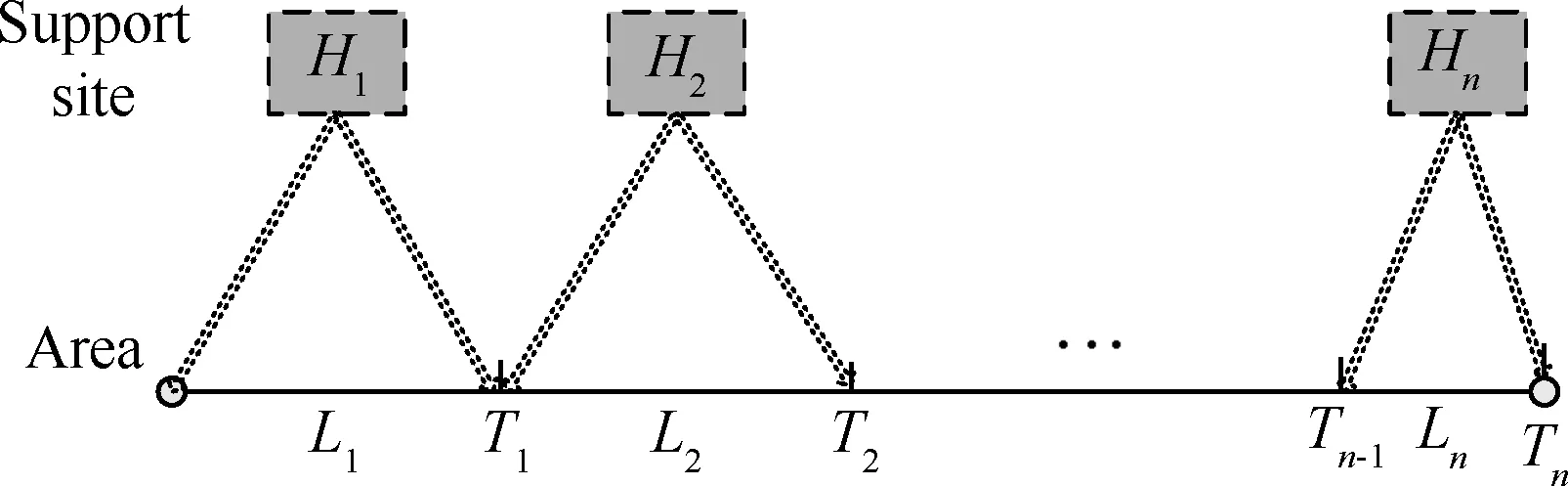
图1 不同区域编队后方保障站点Fig.1 Formation rear support sites at different regions

1.2 条件假设

结合编队执行任务后方站点变更时的备件保障流程，在建模时作如下条件假设：

1) 部件故障规律服从泊松分布。

2) 装备部署现场、保障单元、后方保障基地备件保障实行(s-1,s)连续补给策略。

3) 编队在同一区域执行任务期间，保障单元z到后方站点Hn运输时间恒定。

4) 编队中作战单元仅具备对装备中LRU换件维修能力，保障单元具备一定的LRU维修能力,不具备SRU修理能力。

5) 不考虑同级别站点备件横向补给。

6) 每个区域均由固定站点进行保障，不允许该站点以外的其他站点保障。

2 备件动态供应渠道建模

2.1 备件需求计算

1) 后方站点LRU需求率计算

编队执行任务期间，t时刻作战单元站点j中备件LRU的需求率为

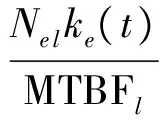
(1)

式中：下标l为第l类LRU；下标e为第e类装备；Ne l为装备e中LRU的装机数；ΜΤΒFl为第l类LRU平均无故障工作时间；ke(t)为站点j中装备e在t时刻工作的数量，当装备不工作时，ke(t)为0。

由于作战单元仅具备LRU更换能力，因此t时刻编队中作战单元对保障单元z产生的LRU需求为

(2)

式中：Echelon(1)为所有作战单元站点j的集合。

若在t时刻，编队后方保障站点为Hn，则后方站点Hn中由保障单元产生的备件需求为所有保障单元不可修的LRU数量,其表达式为

(3)

式中：Echelon(2)为所有保障单元z的集合；rzl为备件LRU在保障单元z的修复概率；πn(t)用来表征t时刻编队是否在第Ln区域，若编队在第Ln区域,取值为1，否则取值为0，πn(t)的表达式为

(4)

2) 后方站点SRU需求率计算

由于作战单元j仅具备LRU更换维修能力，不能修理LRU，因此不会对保障单元z产生SRU需求，而保障单元z对LRU有一定的维修能力，会对LRU中出现故障的SRU进行换件维修。设保障单元z对SRU修复概率为rzi,第l项LRU发生故障是由第i项SRU故障导致的概率为qil，则t时刻保障单元站点z对后方站点Hn产生的SRU需求为站点z不可修的SRU送至后方站点修理的数量，其表达式为

λhzi(z,t)=λzl(t)rzlqil(1-rzi)πn(t)

(5)

t时刻站点Hn在修理LRU时产生的SRU需求为

λhhi(t)=λhl(t)rhlqil

(6)

式中:rhl为站点Hn中LRU的修复概率。

t时刻站点Hn中SRU需求由2部分构成：一是保障单元z不可修的SRU向站点Hn申领的部分；二是站点Hn在修理LRU时产生的SRU部分。因此，根据式(5)和式(6)，可求得t时刻站点Hn中SRU备件需求数为

(7)

2.2 后方基地级站点备件供应渠道计算

2.2.1 SRU供应渠道计算

由于t时刻站点Hn产生的SRU需求数服从λhi(t)的泊松分布，因此t时刻站点Hn正在修理的SRU数量亦服从均值和方差相同的泊松分布[13]，可得t时刻站点Hn正在修理的SRU数量为

(8)

式中：rhi为站点Hn中SRU的修复概率;RThi为站点Hn中SRU的平均维修时间。

编队执行任务期间，保障编队的后方站点可分为2类：一类是后方站点在任务期间无补给；另一类是后方站点可以从外界得到连续补给。

1) 后方站点无外界补给时备件供应渠道计算

若在任务期内，后方站点Hn因地理位置限制无外界补给，则t时刻，站点Hn中SRU备件供应渠道由在修的SRU和不可修SRU这2部分组成，从Tn-1时刻编队进入第Ln区域后，站点Hn累积不可修的SRU数量服从均值和方差相同的泊松分布，其表达式为

(9)

因此t时刻站点Hn中备件SRU供应渠道服从均值和方差相同的泊松分布，均值为

E[Xhi(t)]=DRPhi(t)+DNRPhi(t)

(10)

2) 后方站点实行连续订购策略时备件供应渠道计算

若后方站点Hn中不可修备件可向工业部门订购，则后方站点Hn中备件SRU供应渠道数量由正在修理的部分和订购途中2部分组成，并服从均值和方差相同的泊松分布，均值为

E[Xhi(t)]=

(11)

式中：Bi为第i项SRU订购周期。

根据文献[13]中备件供应渠道概率分布计算公式，t时刻当备件供应渠道差均比(VTMR)相等时，备件供应渠道数量服从泊松分布；当备件供应渠道差均比大于1时，备件供应渠道数服从负二项分布；当备件供应渠道差均比小于1时，备件供应渠道服从二项分布，不同分布参数求取详见文献[8]。由此可求取t时刻后方站点Hn中备件SRU供应渠道数为x个的概率Phi(x,t)。

因此t时刻后方站点Hn中SRU短缺数期望值EBOhi(i,t)和短缺数期望方差VBOhi(i,t)为

(12)

式中：Shl为站点Hn中LRU初始库存数量。

2.2.2 LRU供应渠道计算

由于后方站点在修理LRU时，SRU是LRU修理的物质基础，当SRU短缺时，会造成LRU修理延误，因此与SRU供应渠道来源相比，LRU供应渠道还包括SRU短缺造成LRU维修延误的部分。因此t时刻后方站点Hn备件供应渠道由3部分组成：一是LRU在修数量；二是LRU不可修数量或订购途中数量；三是站点Hn因SRU短缺造成LRU维修延误的数量。其中LRU在修数量、不可修数量、订购数量求取方式与SRU求取该部分方式相同。而站点Hn中因备件SRU短缺造成LRU维修延误部分的数量为

(13)

(14)

方差为[11]

(15)

当站点Hn无外界补给，t时刻站点Hn中备件LRU供应渠道均值为

E[Xhl(t)]=DRPhl(t)+

(16)

式中:Bl为第l项LRU订购周期.

方差为

Var[Xhl(t)]=DRPhl(t)+

(17)

当站点Hn不可修LRU向工业部门订购时，t时刻LRU供应渠道为

E[Xhl(t)]=

(18)

方差为

Var[Xhl(t)]=

(19)

依据后方站点Hn中LRU备件供应渠道均差比与1的大小，由式(12)可求取后方站点Hn中LRU短缺数期望值EBOhl(t)和短缺数期望方差VBOhl(t)。

2.3 中继级站点备件供应渠道计算

1) 保障单元SRU供应渠道计算

由于保障单元仅具备LRU修理能力，不能修理SRU，因此t时刻保障单元z中SRU备件供应渠道由2部分构成：一是后方站点Hn因SRU备件短缺造成本级延误数量；二是正在补给途中的SRU数量。

t时刻，因后方站点Hn中SRU短缺造成站点z保障延误的SRU数量为

(20)

方差为

(21)

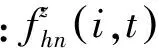
(22)

在任意t时刻，由于保障单元z所在的区域由唯一的后方站点保障，因此依据式(21)和式(22)，可得t时刻保障单元z因上级SRU短缺造成本级延误的数量均值和方差分别为

(23)

(24)

t时刻保障单元z中SRU处于补给途中的数量分为2个阶段求取：第1阶段是编队刚进入第Ln区域执行任务，处于运输途中的数量有一部分是在第Ln-1区域产生的需求，为站点Hn-1运送途中的部分；第2阶段是编队在第Ln区域执行一段时间任务后，站点Hn-1运送的备件全部抵达，运输途中部分全部是站点Hn正在运送的部分，运输途中的数量为

OSTjl(t)=

(25)

式中：OST(n)为编队在第Ln区域时至后方站点Hn的运输时间。

因此t时刻保障单元z中SRU供应渠道均值为

(26)

方差为

(27)

2) 保障单元LRU供应渠道计算

t时刻保障单元z中LRU备件供应渠道由4部分组成：一是保障单元z中正在修理的LRU数量；二是处于补给途中的LRU数量；三是因后方站点Hn中LRU短缺造成本级保障延误的数量；四是本级SRU短缺造成LRU修理延误的数量。

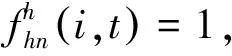
由于作战单元j仅具备LRU更换能力，因此只需求取t时刻作战单元j中LRU备件供应渠道的均值E[Xjl(t)]和方差Var[Xjl(t)]，而t时刻作战单元j中LRU供应渠道由运输途中部分和上级站点LRU短缺造成保障延误2部分构成，其求取方式与保障单元LRU求取方式相同。

3 编队备件期望短缺数计算步骤

根据式(12)可知，要求取t时刻编队中保障单元和作战单元备件期望短缺数，需要已知保障单元和作战单元中在进入第Ln区域执行任务时的备件数量。而编队进入第Ln区域执行任务时的备件数量与第Ln-1区域执行任务期间备件消耗相关。因此先求取编队在第Ln区域执行完任务后，编队剩余备件分布概率，然后将不同剩余备件情况下的备件期望短缺数相加，得到t时刻编队中各站点备件期望短缺数。编队中剩余备件包括保障单元剩余的LRU备件和SRU备件，以及作战单元中LRU备件。各站点不同类型备件剩余数量及期望短缺数计算步骤相同，以计算保障单元SRU剩余备件数量和期望短缺数为例。

3.1 编队剩余备件分布概率计算

根据保障单元SRU备件供应渠道差均比与1的大小，可求得t时刻保障单元z在第Ln区域执行任务期间，SRU供应渠道数为x个的概率Pzi(x,t)。

编队在第Ln-2区域执行完任务，从Tn-2时刻进入第Ln-1区域，若保障单元z在Tn-2时刻剩余SRU备件为yn-2个的概率为Ψzi(yn-2,Tn-2),根据备件库存平衡公式[11]，保障单元z中SRU在Tn-1时刻剩余备件数量为保障单元在Tn-2时刻剩余备件数减去Tn-1时刻保障单元SRU备件供应渠道数，因此Tn-1时刻保障单元中SRU剩余备件为yn-1个的概率为Ψzi(yn-2,Tn-2)Pzi(yn-2-yn-1,Tn-1)。而保障单元在Tn-1时刻剩余SRU备件为yn-1个的概率为保障单元在Tn-2时刻不同剩余备件条件下剩余SRU备件为yn-1个的概率之和。设保障单元z执行任务前携带的SRU数量为Szi,则保障单元在Tn-1时刻剩余SRU备件为yn-1个的概率为

ηzi(n-1)(yn-1,Tn-1)=

Pzi(yn-2-yn-1,Tn-1)]

(28)

因此Tn-1时刻保障单元z中SRU剩余备件期望值为

(29)

方差值为

Var[Szi(Tn-1)]=

{E[Szi(Tn-1)]}2

(30)

根据保障单元z中SRU剩余备件差均比与1大小，可得到保障单元z在Tn-1时刻剩余SRU备件为β个的概率为Ψzi(β,Tn-1)。

3.2 编队备件期望短缺数计算

当站点z在Tn-1时刻剩余SRU备件为β个时，根据式(12),可得到t时刻站点z中SRU备件期望短缺数为

(31)

期望方差为

(32)

Tn-1时刻站点z剩余SRU备件数为β个的概率为Ψzi(β,Tn-1),因此站点z在t时刻LRU备件期望短缺数和期望方差分别为

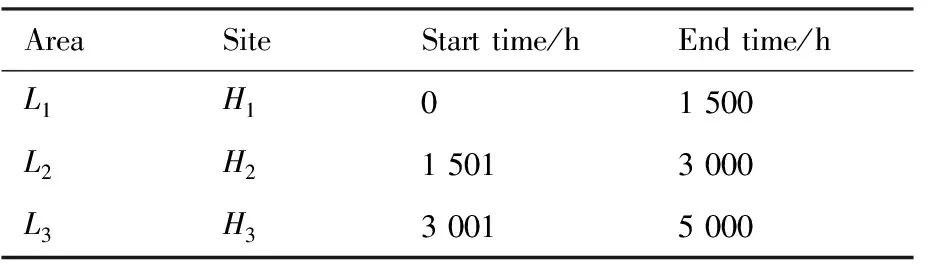
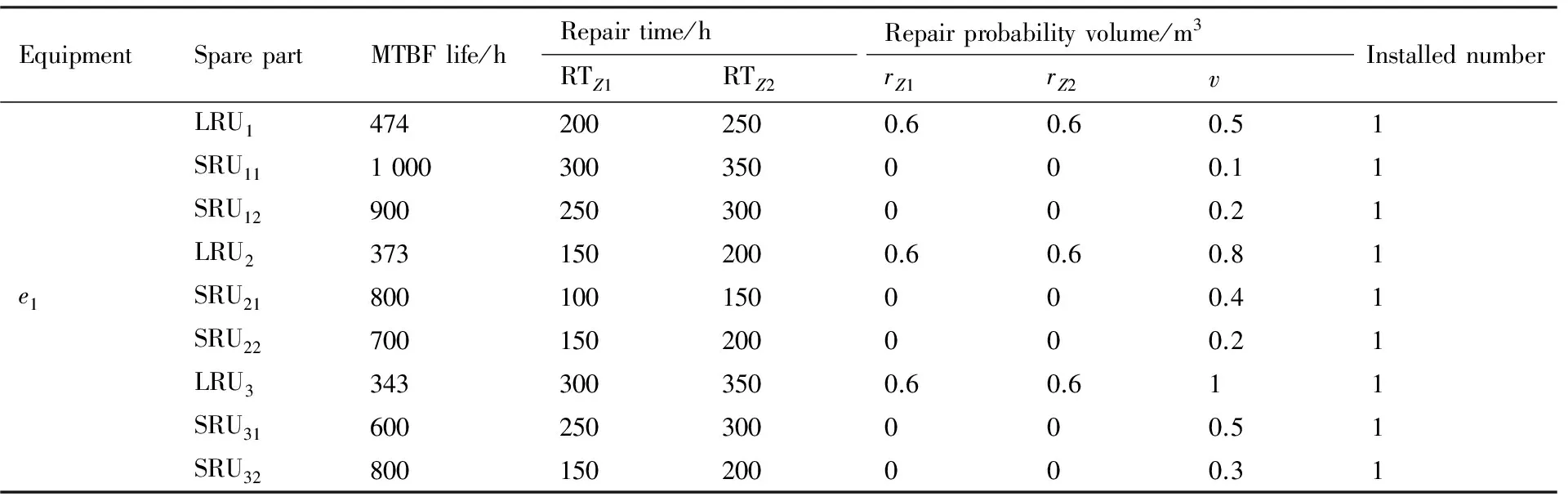
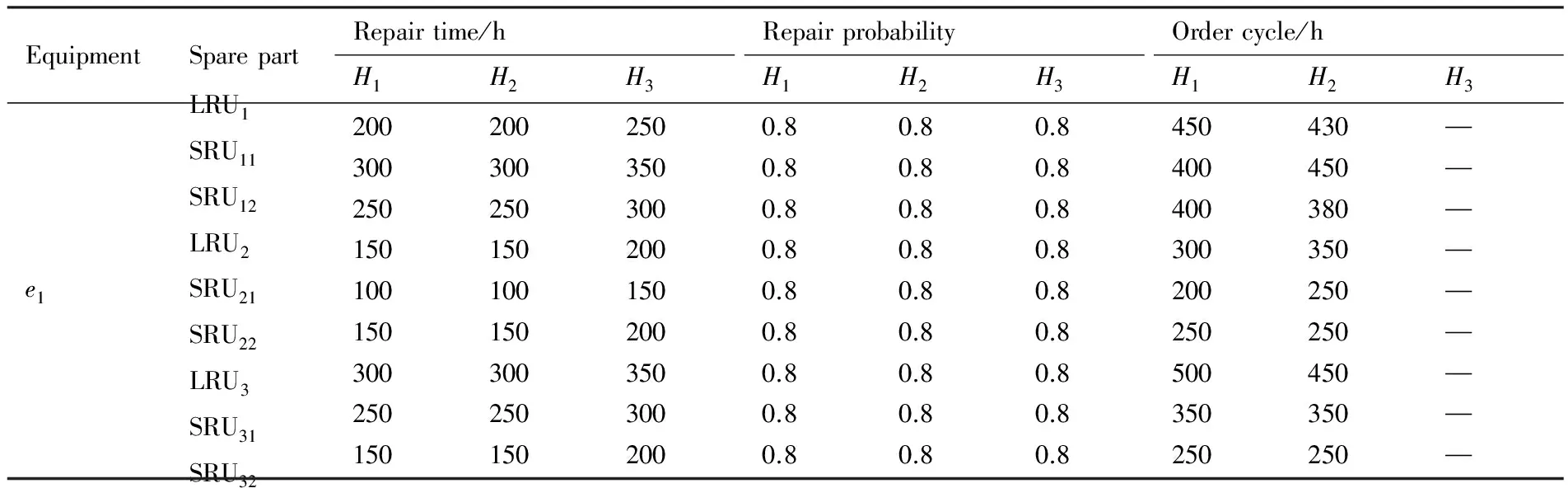
EBOzi(t)=

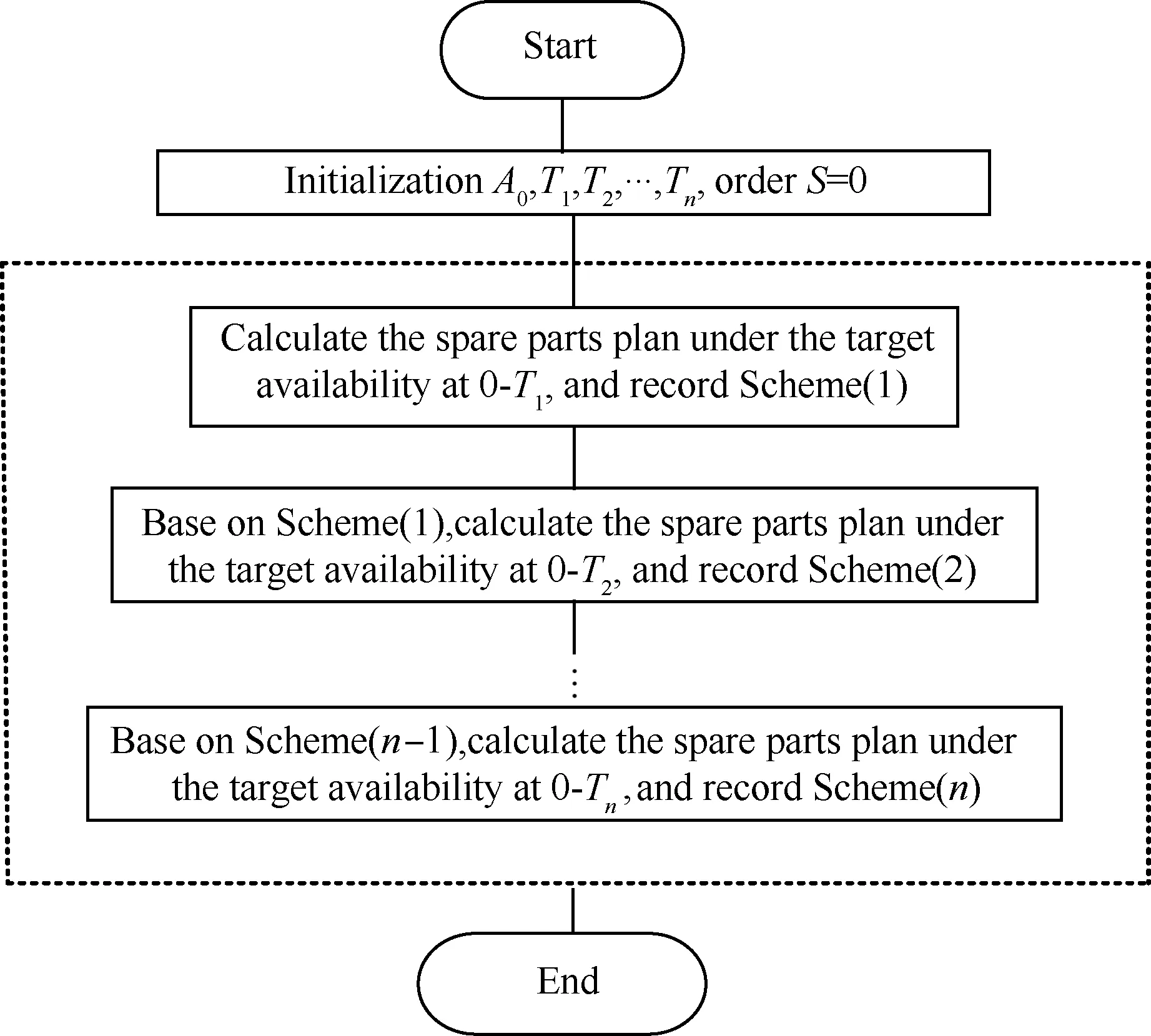
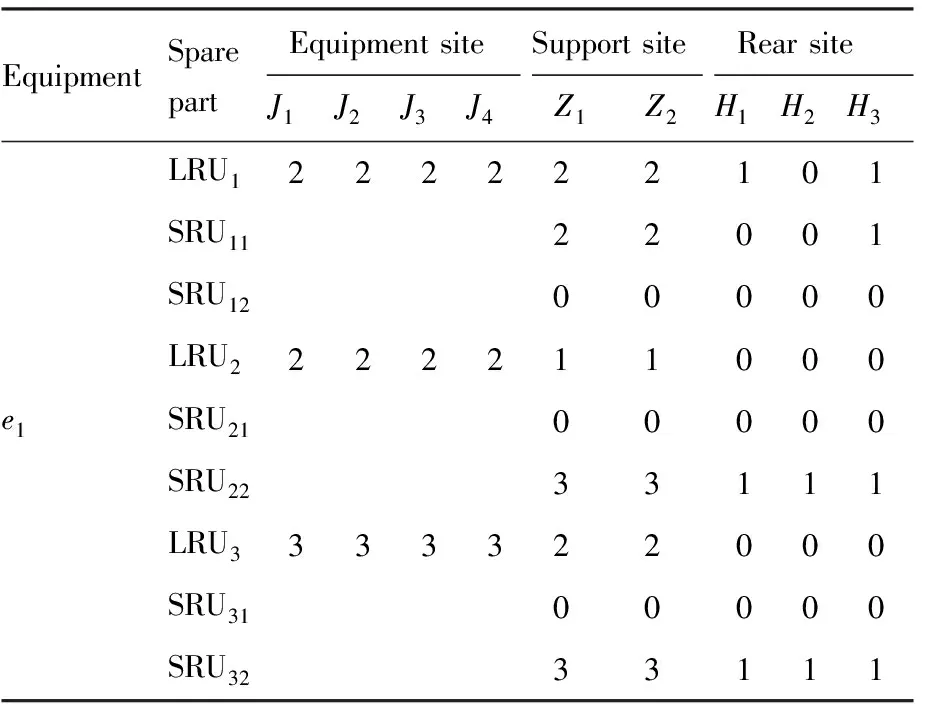
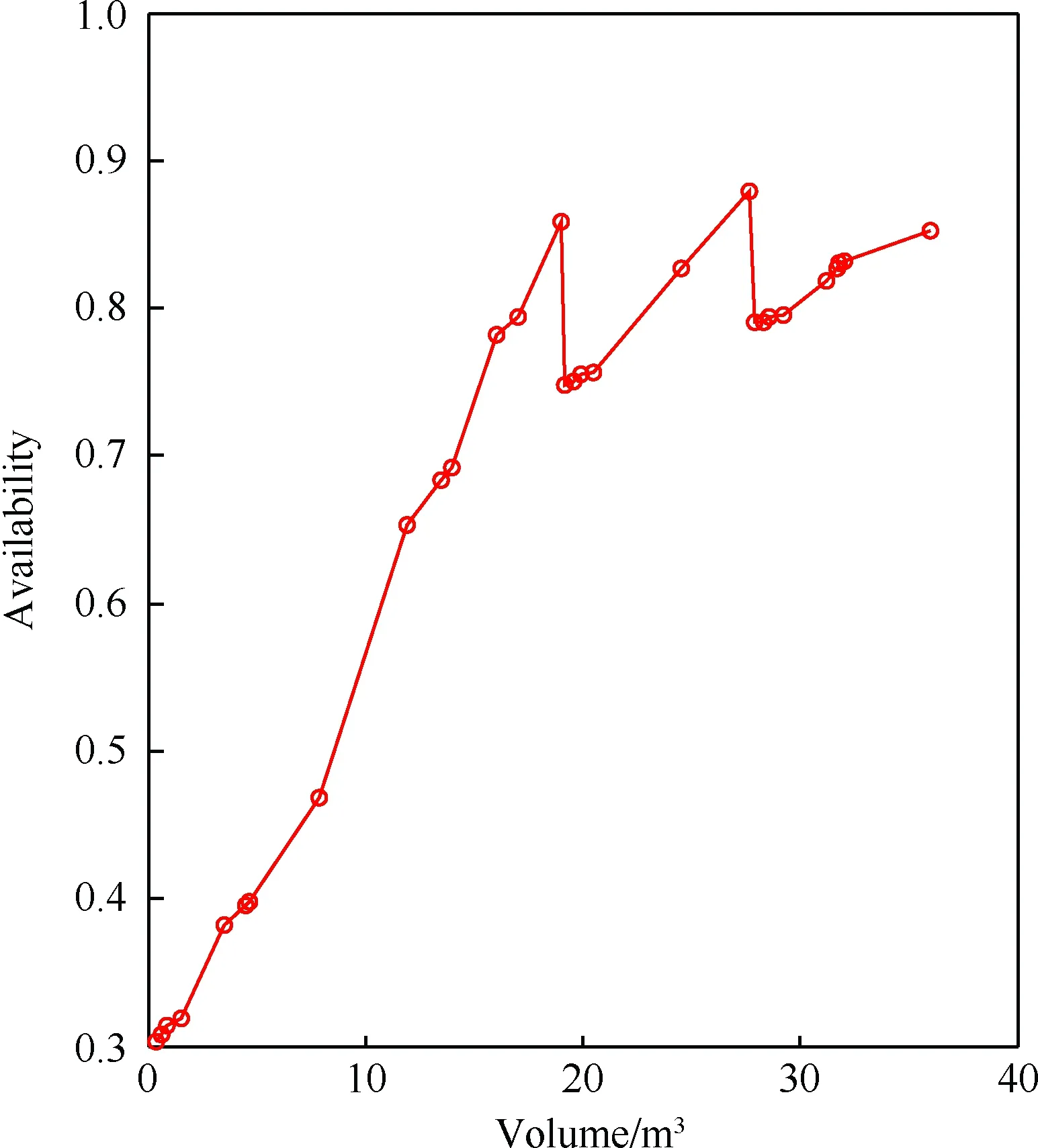
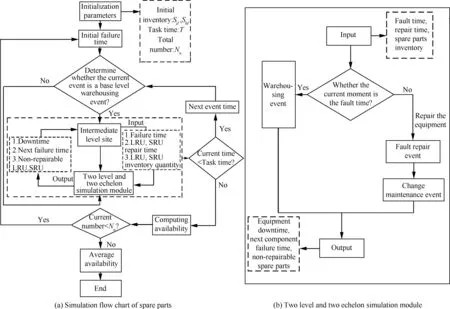
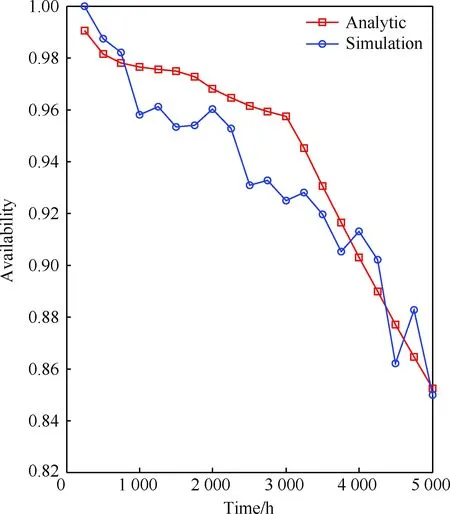
Tn-1

(33)

VBOzi(t)=

Tn-1

(34)

同理，可求取t时刻作战单元j中LRU期望短缺数EBOjl(t)和期望方差VBOjl(t),依据文献[12]可用度求取方式可求得t时刻装备e的可用度Ae(t)。

4 空间约束下分阶段边际优化算法

4.1 标函数

通常装备使用现场站点j备件储存空间有限，因此以使用站点备件贮存空间为约束，以装备可用度为优化目标，其优化模型目标函数为

(35)

式中：Indenture(1)为装备e中所有LRU的集合;Indenture(2)为装备e中LRU下所有SUR的集合;v为备件体积；Sjl、Szl、Shi分别为作战单元j、保障单元z、后方站点h的初始备件数量；vl为LRUl的体积;vi为LRUi的体积;vjconstant为站点j备件储存体积;A0为整个任务期间装备e可用度目标值。

4.2 分阶段分层边际优化算法

边际算法是V-METRIC软件和OPUS软件的核心算法[14-16]。传统的边际算法在迭代过程中确定备件方案时，需要反复计算各项备件加1时，整个任务期内装备e的可用度值。该种方法计算效率较低，本文采用分阶段分层边际优化算法，根据编队经历的区域顺序，实行逐步优化，其优化流程如图2所示。

图2 分阶段优化流程Fig.2 Phased optimization process

步骤1初始化。计算任务时间为Tn、保障系统备件方案为Scheme(n-1)时装备中LRU的可用度，并将可用度值放入矩阵A1,ml、A2,ml。

步骤2确定站点m中LRU备件求解范围。若站点m为装备部署现场站点，且站点m现有备件体积vmtoal大于其贮存体积vmconstant时，则进行m=m+1操作，并继续执行步骤2,否则执行步骤3。

步骤5确定目标可用度值下的最优备件方案。对于任意站点m中非空效益矩阵B1,ml、B2,ml，取所有站点所有备件效益矩阵中第1个效益值放入矩阵C,即C=[B1,m1(1)B1,m2(1) …B1,ml(1)B2,m1(1)B2,m2(1)…B2,ml(1)]，对矩阵中效益值最大的站点备件项目Sml数量加1，计算此时系统可用度Ae，若Ae

步骤6更新效益矩阵C。对效益值最大的备件项目Sml，若是LRU项目，用效益值B1,ml(2)替代矩阵C中原来的效益值B1,ml(1)；若是SRU项目，用效益值B2,mi(2)替代矩阵C中原来的效益值B2,mi(1)，对效益值最大的站点备件项目Smi数量加1，计算此时的系统可用度Ae，若Ae

5 案例分析

5.1 案例计算

图3 不同区域编队保障结构Fig.3 Formation support structure in different regions

由作战单元站点J1、J2和保障单元Z1组成的编队1、站点J3、J4和保障单元Z2组成的编队2均依次在L1、L2、L3这3个区域执行任务，3个区域对应的后方基地站点为H1、H2、H3。L1、L2、L3区域至H1、H2、H3站点的运输时间均值均为100 h，H2至L1、L2、L3的运输时间均值依次为500、100、300 h。H1和H2站点属于国内保障基地，不可修的故障件直接从工业部门订购，H3站点属于海外保障基地，根据上级制定的补给计划，整个任务期间无补给，属于自主保障。编队执行任务期间保障结构如图3所示。2个编队在各区域的任务计划相同，任务时间均为5 000 h，各区域任务起止时刻如表1所示。以每个作战单元站点中雷达装备为例，雷达装备(e1)的装机数为3，部件清单如表2所示，MTBF为备件的平均无故障间隔时间，RTZ1、RTZ2分别为保障单元Z1、Z2修理备件的平均维修时间，rZ1、rZ2为保障单元Z1、Z2的备件修复概率。后方保障基地对雷达装备的保障参数如表3所示。作战单元站点J1、J2、J3、J4储放备件的体积为10 m3，到各自的保障单元的运输时间均为20 h。

当上级要求任务期间装备目标可用度不低于0.85时，首先根据表2中备件信息依次求取使用站点、保障单元、后方站点的备件需求，然后采取由上至下的方法，将每次边际迭代产生的备件方案输入，求取使用现场站点的备件期望短缺数，进而得到装备可用度，直至迭代输入的备件方案使装备可用度≥0.85，整个算法运行结束，得到的备件方案如表4所示。此时作战舰站点备件体积为5.6 m3，边际优化曲线如图4所示。

分析表4可知，作战单元站点(J1、J2、J3、J4)属于装备部署现场站点，由于仅具备装备换件维修能力，因此仅携带LRU备件。而保障单元站点(Z1、Z2)由于具备一定的LRU修复能力，可以采取更换一部分LRU中故障SRU部件来满足作战单元站点的LRU备件需求，因此其携带的LRU备件数量少于装备部署现场站点，多于后方保障站点(H1、H2、H3)；而由于保障单元SRU修复能力为0， 因此无法通过修复SRU故障件满足LRU修理时产生的SRU需求，故保障单元携带的SRU备件多于后方站点携带的SRU备件。后方站点H1、H2不可修的备件可以直接从工业部门订购，而站点H3在整个任务期间处于无补给状态，因此其携带的备件数量多于站点H1和H2。

表1 任务计划时间及后方保障站点Table 1 Mission plan time and rear support sites

表2 装备部件可靠性参数及维修参数Table 2 Reliability parameters and maintenance parameters of equipment components

表3 后方保障站点维修参数Table 3 Maintenance parameters of rear support sites

分析图4中备件边际优化曲线，从图中可知，装备可用度值随备件数不断增加至0.85，而后下降，下降后随着备件数增加可用度又超过0.85，呈现出阶段性规律变化。以前2个阶段为例，对曲线变化进行分析。第1阶段(0～500 h)备件保障系统由编队1、编队2、后方站点H1构成，迭代计算装备可用度为0.85的备件方案，作为第2阶段的初始备件方案;第2阶段(0～3 000 h)为计算编队进入第2区域(1 501～3 000 h)产生备件需求而增加的备件，由于编队在第2阶段的初始备件方案为第1阶段优化得到的备件方案，而编队任务时间由1 500 h增长至3 000 h，因此装备可用度会出现直线下降，随着备件的优化迭代，装备可用度逐渐超过0.85。

表4 目标可用度为0.85时的备件配置方案

图4 目标可用度为0.85时边际优化曲线Fig.4 Marginal optimization curve when the target availability is 0.85

若整个任务期间，编队均由处于中间时间段的后方站点H2保障，比较后方站点各类备件总数量相同条件下，固定保障结构和动态保障结构装备可用度随时间的变化。后方站点H1，H2，H3中LRU1，SRU11，SRU12，LRU2…等不同类型备件数量之和依次为2、1、0、0、0、3、0、0、3，将其作为固定保障结构时后方站点H2的初始备件方案。采用本文模型计算得到2种保障结构下可用度随时间的变化如图5所示。

图5 两种保障结构下可用度随时间变化Fig.5 Variation of availability with time under two support structures

从图5中动态保障下装备可用度随时间的变化可知，在第1区域(0～1 500 h)和第2区域(1 501～3 000 h)，编队刚进入这2个区域时，可用度下降快，而后装备可用度下降趋于平缓，且在这2个区域编队装备可用度下降速度接近，而在3 001～5 000 h装备可用度下降速度明显增加。这是因为编队在L1区域和L2区域执行任务时，后方保障站点H1和H2不可修备件可通过向工业部门订购进行补充，随着编队在各区域任务时间的推进，处于维修运输周转的备件基本不变，装备可用度由非稳态逐渐趋向稳态。但由于编队进入L2区域时，编队一部分备件处于维修运输周转状态，因此其剩余的备件数量较初始携带的备件数量少，而保障L2区域的站点H2初始备件配置数略少于H1站点，因此编队进入L2区域后装备可用度比在L1区域时低。当编队从L2进入L3区域时，由于保障L3区域的后方站点备件修复概率为0.8，不可修备件无法从外界得到补给，随着时间的推进，不可修的备件越来越多，因此装备可用度随时间下降速度较前2个阶段更快。

而从固定保障结构下装备可用度随时间的变化可知：在整个任务期间，固定保障结构下装备可用度低于动态保障结构下装备可用度，且两者之间的差值除在第1区域时间段内差距变大外，在之后的区域时间段内逐步接近。这是因为：在第1区域内(0～1 500 h)，即使固定保障结构下后方站点的初始备件多于动态保障结构下后方站点的初始备件数，但由于固定保障结构下处于运输周转的备件数远大于动态保障结构下处于运输周转的备件数，因此其可用度下降速度较动态保障结构快；在第2区域(1 501～3 000 h)，因固定保障结构下的编队到后方站点的运输时间与动态保障结构中编队到后方站点的运输时间均为100 h，因此2种保障结构下装备可用度下降速度较为接近，而备件处于运输周转的数量较第1区域时少，因此固定保障结构下装备可用度在1 500 h之后略有提升，其装备可用度较第1区域期间接近动态保障结构下装备可用度；在第3区域，虽然固定保障结构下编队距站点H2运输时间为300 h，较动态保障结构下编队距后方站点H3运输时间长100 h，但由于站点H3的不可修备件无法向工业部门订购，因此固定保障体系下装备可用度越来越接近动态保障结构下装备可用度。

5.2 案例仿真验证

依据备件保障流程，采用蒙特卡罗方法对编队整个任务期间备件保障过程进行仿真建模，将编队中保障单元与作战单元之间备件保障作为一个两级两层仿真模块，嵌入如图6(a)所示仿真流程中，两级两层仿真模块如图6(b)所示。

图6 编队任务期间备件保障仿真流程Fig.6 Simulation flow chart of spare parts support during formation mission

将表4备件方案输入仿真模型，当仿真次数Nu=200时，分别计算任务时间T=250,500,750,1 000,…,5 000 h时的装备可用度，得到的仿真值与解析值对比如图7所示。由图可知，装备可用度解析值与仿真值变化趋势一致，同一时刻两者最大误差绝对值不超过4%，因此动态保障体系下备件保障模型建立正确。

图7 仿真模型与解析模型可用度对比结果Fig.7 Comparison of availability between simulation model and analytic model

6 结 论

本文针对作战编队任务期间后方保障站点变更的情况，基于METRIC理论，建立了动态保障结构下备件配置优化模型和蒙特卡罗仿真模型。结果表明：

1) 当编队执行远距离任务时，设立前沿保障站点或实行区域就近的多站点保障方式比固定一个后方站点的保障方式能有效提高装备的可用度。

2) 在编队与后方站点实行连续补给策略下，任务期间编队由多个后方站点保障的方式能降低备件运输成本。

3) 仿真模型与解析模型结果一致，表明本文建模方法可行，模型可为编队远洋任务期间，设置前沿保障站点位置提供模型参考，为舰艇、飞机执行远洋任务制定备件方案提供辅助决策。

[1] ISAACSON K E, BOREN P. Dyna-METRIC Version 6: An advanced capability assessment model: R-4214-AF[R]. Santa Monica, CA: RAND Corporation, 1993.

[2] LAU H C, SONG H, SEE T C, et al. Evaluation of time-varying availability in multi-echelon spare parts systems with passivation[J].European Journal of Operational Research, 2006, 170(1): 91-105.

[3] 王睿，雷红伟，彭英武，等. 战时任务条件下舰艇装备多级备件优化[J].上海交通大学学报, 2013,47(3):398-403.

WANG R, LEI H W, PENG Y W, et al. Optimal of warship spare parts in the scenario of wartime mission[J]. Journal of Shanghai Jiaotong University, 2013, 47(3):398-403(in Chinese).

[4] 周亮，李庆民，王睿，等.K/N(G)冗余结构下随舰备件配置方案[J].系统工程与电子技术,2015,37(12):2785-2790.

ZHOU L, LI Q M, WANG R, et al. Spare parts allocation scheme with ship forK/N(G) redundant structure[J]. Systems Engineering and Electronics,2015,37(12):2785-2790(in Chinese).

[5] 徐立，李庆民，李华，等．有限维修能力下作战单元时变可用度评估模型[J].国防科技大学学报，2016, 38(1):114-121.

XU L, LI Q M, LI H, et al. Evaluation model of time-varying availability for combat units under finite repair capacity[J].Journal of National University of Defense Technology，2016,38(1):114-121(in Chinese).

[6] 李华，李庆民，刘任洋.任务期内多层级不完全修复件的可用度评估[J].系统工程与电子技术, 2016,38(2):476-481.

LI H,LI Q M,LIU R Y. Evualtion of availability for multi-indenture partial repairable spares during the mission[J].Systems Engineering and Electronics,2016,38(2):476-481(in Chinese).

[7] 刘勇，武昌，李阳，等．两级备件保障系统的装备时变可用度评估模型[J]．兵工学报，2010，31(2)：253-256．

LIU Y,WU C,LI Y, et al. Evaulation model of equipment time varying availability in two echelon spare support system[J]. Acta Armamentarii，2010，31(2)：253-256(in Chinese)．

[8] 周亮，彭英武，李庆民，等.串件拼修策略下不完全修复件可用度评估建模[J].系统工程与电子技术，2017,39(5):1065-1071.

ZHOU L, PENG Y W, LI Q M,et al. Time-varying availability evaluation modeling of incomplete repair parts under cannibalization [J].Systems Engineering and Electroics, 2017,39(5):1065-1071 (in Chineses).

[9] 周亮，李庆民，彭英武，等. 串件拼修对策下K/N(G)结构系统可用度评估建模[J].航空学报, 2017, 38(4): 220319.

ZHOU L, LI Q M, PENG Y W, et al. Availability evaluation modeling forK/N(G) structure system with cannibalization[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(4): 220319 (in Chinese)．

[10] KLINGER K M. The application of a readiness-based sparing model to foreign military sales: AD-A280629 [R].1994.

[11] 王慎，李庆民，彭英武. 串件拼修对策下两级备件维修供应系统动态管理模型[J]. 航空学报，2013，34(6)：1326-1335．

WANG S,LI Q M,PENG Y W. Dynamic management model of two-echelon maintence supply system for spare parts with cannibalization[J]. Acta Aeronautica et Astronautica Sinica, 2013, 34(6): 1326-1335(in Chinese)．

[12] BÜYÜKKURT M D, PARLAR M. A comparison of allocation policies in a two-echelon repairable-item inventory model[J]. International Journal of Production Economics, 1993, 29(3): 291-302.

[13] SHERBROOKE C C. Optimal inventory modeling of systems: Multi-echelon techniques[M]. 2nd ed. Norwell,MA: Kluwer Academic Publishers, 2004.

[14] ZHOU L, LI Q M, LIU R Y. Optimal inventory control of spare parts based on storage availability[C]∥28th Chinese Control and Decision Conference, 2016: 6409-6414.

[15] 任敏，陈全庆，沈震.备件供应学[M].北京：国防工业出版社, 2013:278-289.

REN M, CHEN Q Q, SHEN Z. Spare parts supply[M]. Beijing: National Defence Industry Press, 2013:278-289(in Chinese).

[16] TYSSELAND B E. Spare parts optimization process and results: OPUS10 cases in the Norwegian Defence[J]. International Journal of Physical Distribution & Logistics Management, 2009, 39(1): 8-27.

Optimizationmodelformulti-levelandmulti-echelonsparepartallocationindynamicsupportstructure

ZHOULiang1，LIQingmin2,*，PENGYingwu3，LIHua3

1.NationalKeyLaboratoryforVesselIntegratedPowerSystemTechnology,NavalUniversityofEngineering,Wuhan430033,China2.OfficeofResearchandDevelopment,NavalUniversityofEngineering,Wuhan430033,China3.DepartmentofWeaponryEngineering,NavalUniversityofEngineering,Wuhan430033,China

Inlongtimeandlongdistancetasksofcombatformation,thesupportsiteofcombatfleetwouldchange.Consideringthecharacteristicsofmilitarysupport,thedistributionlawofremainingsparepartsiscalculatedbasedonMulti-EchelonTechniqueforRecoverableItemControl(METRIC)theory,andthemodelforsparepartsupportbasedontimevaryingavailabilityisestablishedforthedynamicsupportsystem.Withthestoragespaceofsparepartsastheconstraintandthedegreeofavailabilityasthegoal,amodelforphasedmarginaloptimizationisestablished.Anexampleispresented,andtheoptimizationofsparepartsiscarriedoutbyusingthestagemarginalalgorithm.Thevariationofequipmentavailabilitywithtimeinthedynamicsupportstructureandthefixedsupportstructureiscomparedandanalyzed,andMonteCarlosimulationmethodisusedtoverifythecase.Theresultsshowthattheavailabilityofequipmentcanbeeffectivelyimprovedbyadoptingmultipledepotsecuritymethods.Theerrorbetweenthesimulationresultsandtheanalyticalresultsiswithin4%.Themodelproposedcanprovideassistantdecisiontoolfordecisionmakerstomakesparepartplan.

dynamicsupport;multi-echelontechniqueforrecoverableitemcontrol(METRIC);remainingspareparts;phase;marginal;MonteCarlosimulation

2016-09-29；Revised2016-11-09；Accepted2017-02-20；Publishedonline2017-03-031902

URL：http://hkxb.buaa.edu.cn/CN/html/20171114.html

s：NationalDefencePre-researchFoundation(51327020105,51304010206)

.E-maillicheng001@hotmail.com

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.320822

V125.7；E917；TJ07

A

1000-6893(2017)11-220822-13

2016-09-29；退修日期2016-11-09；录用日期2017-02-20；< class="emphasis_bold">网络出版时间

时间：2017-03-031902

http://hkxb.buaa.edu.cn/CN/html/20171114.html

国防预研基金 (51327020105,51304010206)

.E-maillicheng001@hotmail.com

周亮，李庆民，彭英武，等.动态保障结构下多级多层备件配置优化建模J.航空学报，2017，38(11):220822.ZHOUL,LIQM,PENGYW,etal.Optimizationmodelformulti-levelandmulti-echelonsparepartallocationindynamicsupportstructureJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):220822.

(责任编辑：苏磊,王娇)