可压缩流动激波装配在格心型有限体积法中的应用

邹东阳，刘君, *，邹丽

1.大连理工大学 航空航天学院，大连 116024 2.大连理工大学 船舶工程学院，大连 116024

可压缩流动激波装配在格心型有限体积法中的应用

邹东阳1，刘君1, *，邹丽2

1.大连理工大学 航空航天学院，大连 116024 2.大连理工大学 船舶工程学院，大连 116024

发展了一种基于格心型有限体积方法(FVM)的激波装配算法。通过定义网格节点属性可以灵活调用激波装配和激波捕捉计算方法。在使用激波装配方法时，激波节点运动速度和下游运动速度通过Rankine-Hugoniot(R-H)关系式获得，同时采用非结构动网格技术描述激波的运动以及调整其他网格节点的位置。流过激波面元的通量为上游单元的基本通量，物理概念更加清晰，通量计算也更为准确。在计算过程中，网格节点属性可以发生变化，以此实现对带有拓扑变化流场的描述。数值试验表明：本文提出的计算方法不但具有较高的计算精度，同时能有效地避免由于捕捉激波而出现的数值问题。

激波装配;非结构动网格;有限体积法(FVM);计算流体力学;可压缩流动

当流动速度大于声速时，流动特性会发生很大的变化，非线性效应也更加明显。很多在低速流动研究中应用良好的数值方法不再适用，需要发展出针对高超声速流动更加有效的模拟手段[1]。关于高超声速流动的数值研究在航空航天领域已历经了数十年，并且产生了大量的研究成果，极大地推进了该领域的发展。但是对于激波，这一在高超声速流动中出现的重要物理现象的模拟仍然是一个重要的挑战。

计算激波一个最直接的办法就是使用激波装配法，即将激波面看做一个间断，使其两侧的物理量满足Rankine-Hugoniot(R-H)关系式。这种方式在计算流体力学初期作为一种重要的研究手段被广泛应用于高超声速流动的数值计算中[2-3]。但是，激波装配方法由于网格拓扑结构的限制很难应用于具有内嵌激波等复杂波系的实际问题中[4]。

从20世纪80年代起，基于捕捉算法的计算流体力学得到了迅速发展[5-12]，被广泛用于航空航天、船舶、气象、环境、生物医学等领域。不可否认捕捉算法的提出极大地促进了计算流体力学的发展。但是，当面对含有强激波的高超声速流动时，这些在光滑区域应用良好的计算方法，在激波附近最终还是降为一阶，并且在强激波波后还会有非物理振荡现象出现[13]。这些都是由于捕捉方法本身的设计缺陷所导致的。相对于激波阵面，波前流动为超声速流动。按照超声速流动特点，上游流动不应受到下游流动的影响，但是对于“守恒格式”的激波捕捉方法来说却不可能做到。处于激波附近的上游网格单元在计算时需要使用下游信息，否则具有守恒性的流动参数无法穿过激波。所以，从这点来说捕捉方法在构造时就与激波的物理特点相矛盾[14]。

由于激波捕捉方法存在缺陷不得不重新审视传统的激波装配方法。文献[15-17]将激波装配方法同高精度计算方法相结合，利用激波装配方法处理激波，在光滑流域使用高精度计算方法，得到全场一致的高精度计算结果。从某种意义上而言，这种做法为未来CFD发展指明了一个方向。但是在这些文献中，激波装配仍是在结构网格上进行的，所以也只是针对弓形激波进行处理，并未涉及到较为复杂的内嵌激波等。激波装配的主要问题是因为拓扑关系造成的,传统的激波装配方法主要依赖的是结构网格，这使得很难通过结构的网格关系来描述具有非结构特点的激波相交等复杂问题。自然而然，就会想到如果从底层改变使用的网格结构可能会大大简化原有装配方法所遇到的困难。Paciorri等[18-22]将Moretti[23]的浮动激波装配方法推广到非结构网格体系下，大大简化了传统激波装配方法，并在很多问题上得以成功应用。Paciorri等采用的是格点型有限体积，要求激波在背景网格上进行滑动。激波运动到新的位置时，通过挖洞处理将表征激波的曲线/面嵌入计算网格，开始进行计算。激波运动后挖洞区域由原始的计算网格填充，对应节点参数通过插值获得。与他们的处理方法不同，刘君等提出基于非结构动网格技术的激波装配方法，激波属于网格的一部分，激波节点的移动带动其他网格节点的运动，计算过程中无需插值，该方法被成功用于求解许多定常/非定常流动问题[24-25]。

本文在非结构激波装配方法研究工作的基础上，建立了一种激波装配/捕捉混合算法，通过对网格节点定义，实现不同的求解算法之间的灵活调用。

1 计算方法

从1998年开始，本文作者所在的课题组一直在从事非结构动网格技术相关的工作，并形成了一套具有特色的流体计算软件[26]。本文在原来代码的基础上进一步开展高超声速流动计算研究，创新性地将激波装配技术与原有CFD求解器有机结合起来。为了能够更清晰地介绍本文的工作，新的计算软件命名为MCFs。采用MCFs进行流动模拟时，3种形式的数值解可能出现。① 捕捉解：在流场中没有激波点被定义，整个流动完全采用捕捉方法进行计算。② 装配解：对流场中出现的激波都进行了定义，激波相关参数完全由装配方法确定。③ 混合解：顾名思义流场中出现的激波部分被定义了，部分激波参数采用装配方法定义得到。

本节首先对原有的激波捕捉方法和非结构动网格技术进行简单介绍，然后通过一个二维流动对激波装配方法相关内容进行详细说明。

1.1 激波捕捉方法

考虑无黏流动，控制方程为时间依赖的Euler方程。ALE(Arbitrary Lagrange-Euler)描述下积分形式的Euler方程可以写为

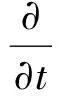
(1)

式中：Ω为控制单元；∂Ω为控制单元界面；xc为网格运动速度；Q为守恒型变量向量；Fc为对流通量向量；n为界面外法线向量；V为控制体体积；S为控制体面元面积。并且有

(2)

采用格心型有限体积法(FVM)用于空间离散，时间推进采用四步龙格-库塔(R-K)方法。第i个单元的控制方程可以写成如下半离散形式：

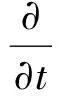
(3)

式中：Nf为第i个控制单元所包含的面元数量；Fk、nk和Sk分别为控制体第k个面元通量、外法线方向和面积。

1.2 非结构动网格技术

在本文中，网格变形技术使用弹簧近似法[27]。当边界运动后，移动内部网格节点，以此来使整个系统的节点达到受力平衡，从而确定网格点的新位置。如图1所示，考虑弹簧系统内任意节点i,节点j为与之相连的节点。根据Hooke定律，节点i受力可以写为

(4)

式中：Kij为节点i和j之间的弹簧倔强系数；Ni为节点i邻居节点的个数。省略中间推导过程，网格点i新坐标位置可以通过如下迭代方程进行确定：

(5)

考虑折穿和扭转效应，弹簧倔强系数的计算公式可以写为

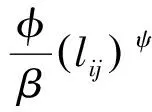
(6)

式中：φ和ψ为弹簧刚度的修正因子,增加φ的值可以提高边界处弹簧的刚度，这样边界节点的运动引起的内部网格变形会传递得更远;β用来规定弹簧刚度，以防出现折穿现象。

当边界节点运动位置过大时，单纯地使用网格变形技术已经无法保证计算网格具有较高的网格质量，这时需要进行网格重构。重构后的网格通过网格间信息传递技术对流场参数进行插值。可以证明，对于时空二阶格式采用信息传递技术不增加插值误差[28]。

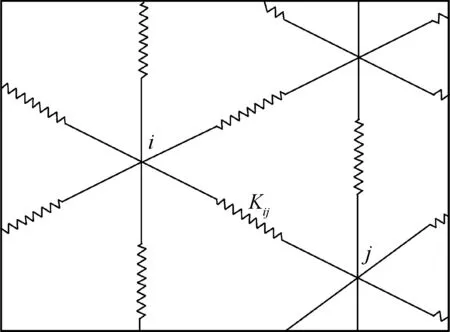
图1 弹簧模型示意图Fig.1 Sketch of springs analogies

1.3 激波装配方法

1.3.1 激波点标识

为了直观地对本文中的激波装配方法进行介绍，考虑如图2所示的一个含有激波的二维流场。在使用MCFs计算程序进行流动计算前，首先采用三角形单元对全场进行离散，离散后的网格节点被标记为普通节点(O)和激波节点(S)两种。激波节点和普通节点相比，在激波节点上存在两组或多组参数，而在普通节点上有且只有一组参数。

值得说明的是：对于定常问题，可以利用捕捉方法得到一个初场，然后通过一些相关辨识技术得到初始激波位置。将符合位置条件的网格节点标记为激波点，经过迭代收敛过程后，最终得到稳定的流场。对于非定常问题，在计算过程中有时候存在激波的生成以及湮灭，所以在计算过程中需要使用更加准确的激波辨识方法。

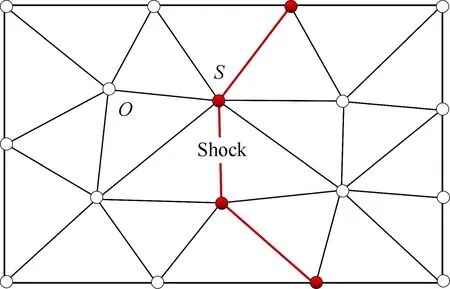
图2 网格节点属性定义Fig.2 Definition of properties of grid nodes

1.3.2 激波参数确定

由于本文采用的捕捉方法为格心型有限体积法，因此需要通过格心参数平均得到格点参数。对于普通节点来讲，只需要将与该节点相邻的所有单元进行加权平均即可得到位于该节点的流动参数。而对于激波节点来说，由于其包含两组流动参数，一组为上游流动参数，一组为下游流动参数。因此在通过单元格心参数来确定格点参数之前需要判断相邻单元位于激波上游还是下游。在激波节点的标记完成后，将所有节点都属于激波节点的面元标记为激波面元。激波面元可以看做是激波阵面的离散，这些面元可以将流动区域分割成两个部分，一部分为低压区，位于激波上游；一部分为高压区，位于激波下游。通过比较激波面元两侧单元熵sL和sR的大小来判断标识上下游单元。熵大的单元属于下游单元，熵小的单元属于上游单元。在上下游单元确定之后，激波节点上游参数Vu=[ρuuupu]T和下游参数Vd=[ρdudpd]T可以通过式(7)进行确定：

(7)

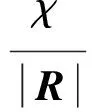
χ={0Maτ k≤-1

1Maτ k>-1

(8)

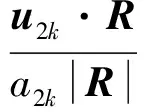
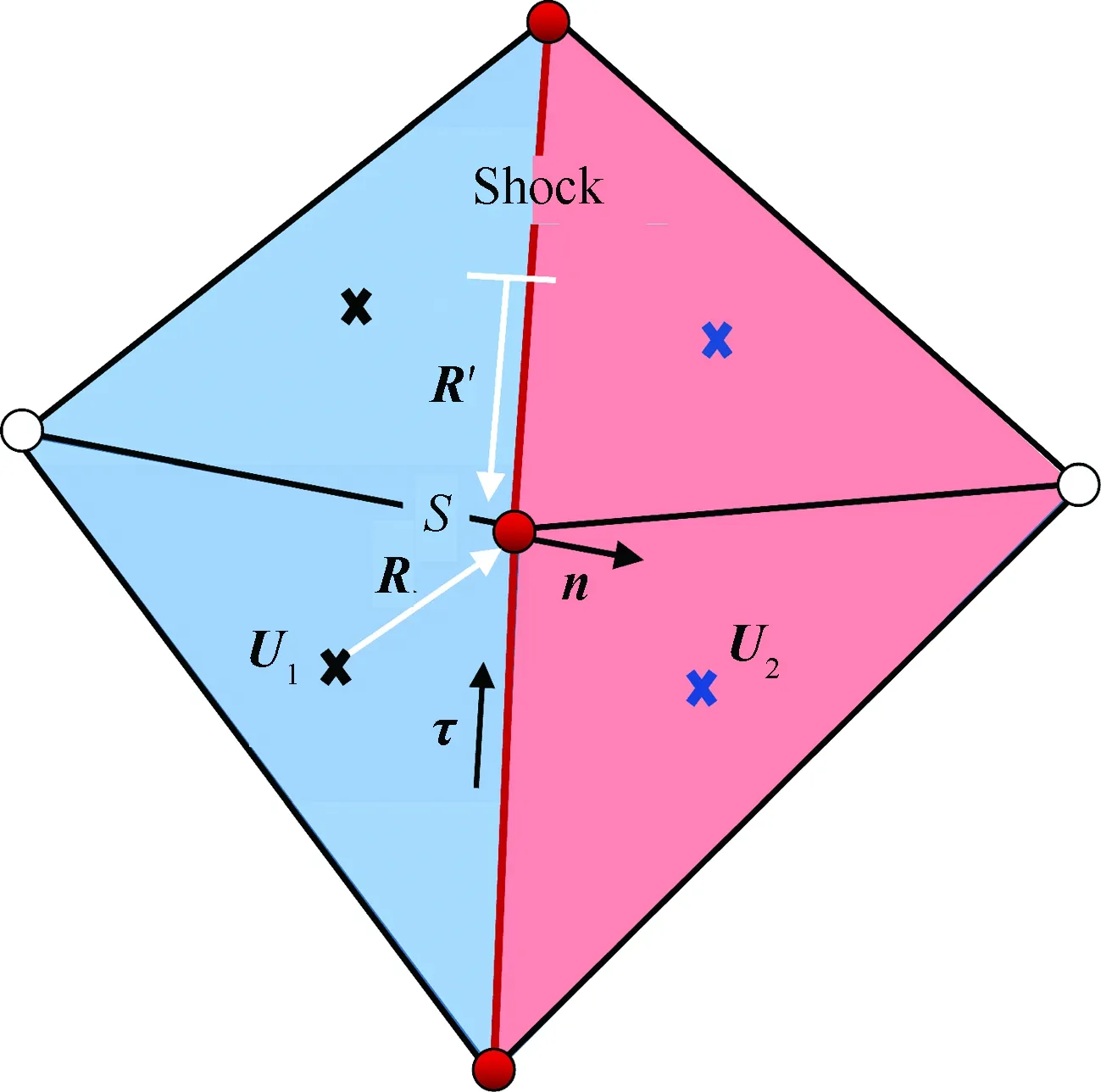
图3 激波节点参数确定Fig.3 Determination of shock nodes parameters

同时，也可以通过激波面元法向确定出激波点的法向n为

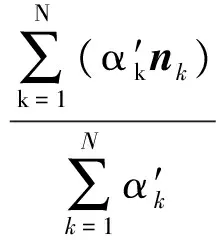
(9)

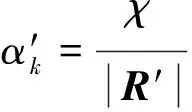
通过上述计算方法将单元格心参数平均到格点上，得到激波节点上的上下游参数Vu和Vd。对于上游流动区域来说，其位于间断的上游，流动信息由上游单元通过间断流向下游。在激波坐标系下，上游流动为超声速流动，因此处于下游的间断不会对上游单元产生影响。也就是说，在激波上游使用捕捉方法获得的流动信息是准确的，即上游流动参数Vu不需要重新确定。由于下游流动区域位于间断下游，熵、涡量以及向前运动的声波等信息都是从间断传播过来的，所以使用捕捉方法得到的下游区域的流动计算结果都不是正确的，即下游流动参数Vd需要重新确定。

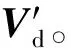
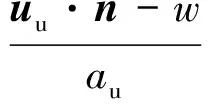
(10)

式中：au为上游区域的声速。根据激波上游参数，可以得到

(11)

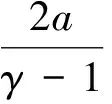
(12)

将式(11)和式(12)合成一个关于Mau,rel的方程：

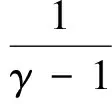
(13)

可以看出，式(13)左侧随Mau,rel线性变化。因此采用牛顿公式可以很容易地求解出来流马赫数在激波法向的相对分量Mau,rel。Mau,rel一旦确定，其他4个未知参数都可以相继得到。

1.3.3 激波通量计算

在格心型有限体积方法中，需要求解各个单元界面的流动通量。对于普通面元来说，通过各种通量计算方法在单元界面上进行通量分解，进而求出各个单元的通量值。而对于激波面元来说，流过激波面元的通量计算方法要更为简单。由前文分析可知，对于激波上游而言，其流动相对于激波面为超声速的。激波间断位于单元下游，可以视为上游单元的超声速出口，因此从上游流过激波面元的通量可以表示为

(14)

1.3.4 网格点运动

1.3.2节在确定激波节点下游流动参数的同时也确定了激波点的运动速度。本文采用非结构动网格技术描述激波节点的运动。根据计算的激波点速度w以及激波点法向n可以确定在此时间步内节点运动的位移为w·n·Δt。如图4所示，在激波节点的运动确定后，通过弹簧近似方法确定其他普通网格节点在新时刻的位置，从而得到新时刻的计算网格。

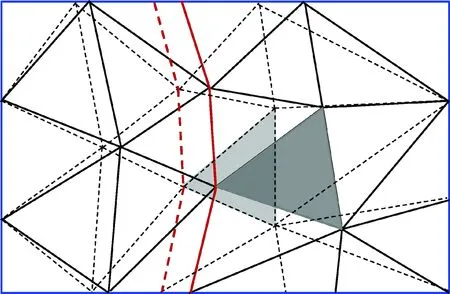
Solid line: grids at T=t; Dashed line: grids at T=t+Δt图4 网格节点运动示意图Fig.4 Sketch of grid nodes motion

2 算例测试

本文通过将提出的计算方法应用到3个二维算例中来验证该方法的可行性。同时，通过比较使用激波装配和不使用激波装配的计算结果来对该方法在计算激波时的特性进行说明。

2.1 超声速圆柱绕流

考虑马赫数Ma=20的高超声速流动经过一个半径为L的无限长圆柱的问题。如图5所示，计算域为包裹半圆柱的类扇形区域。作为一个含有激波的简单问题，文献[29]对该问题进行过研究。因此有很多结果可以用来考核本文计算结果的好坏。

采用POINTWISE进行网格划分，网格类型选择非结构的三角形单元。离散时控制参数选择Δ=0.1L,计算域离散后总共包含1 460个均匀分布的网格单元。

使用激波捕捉方法获得激波装配的初始流场，根据捕捉流场判断出激波的大致位置，对相应位置上的网格节点进行标记，形成计算所需的激波节点数据链表。图6中Iter0给出了标记出的初始激波。由于激波与计算网格的面元相匹配，所以给出的初始激波是一条不规则的曲线。在激波节点以及激波面元定义后，采用本文提出的装配方法计算激波面元上的通量以及激波节点运动速度，同时采用非结构动网格技术调整其他普通网格节点的位置以避免计算网格由于激波节点的运动而发生畸变。若干步迭代后，表征激波的曲线逐步光滑，波前后的流动逐步趋于稳定。

图5 计算区域Fig.5 Computational domain

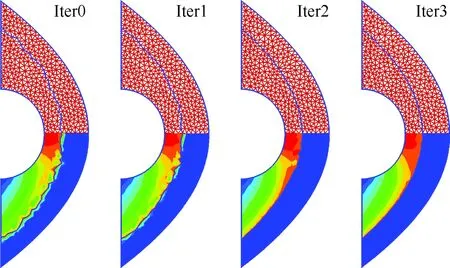
图6 激波收敛过程Fig.6 Process of shock wave convergence

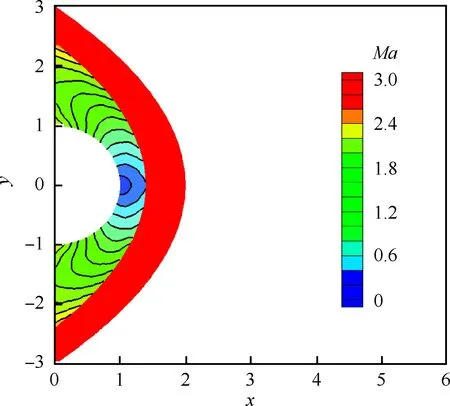
图7 计算的马赫数云图Fig.7 Computed Mach number iso-contours

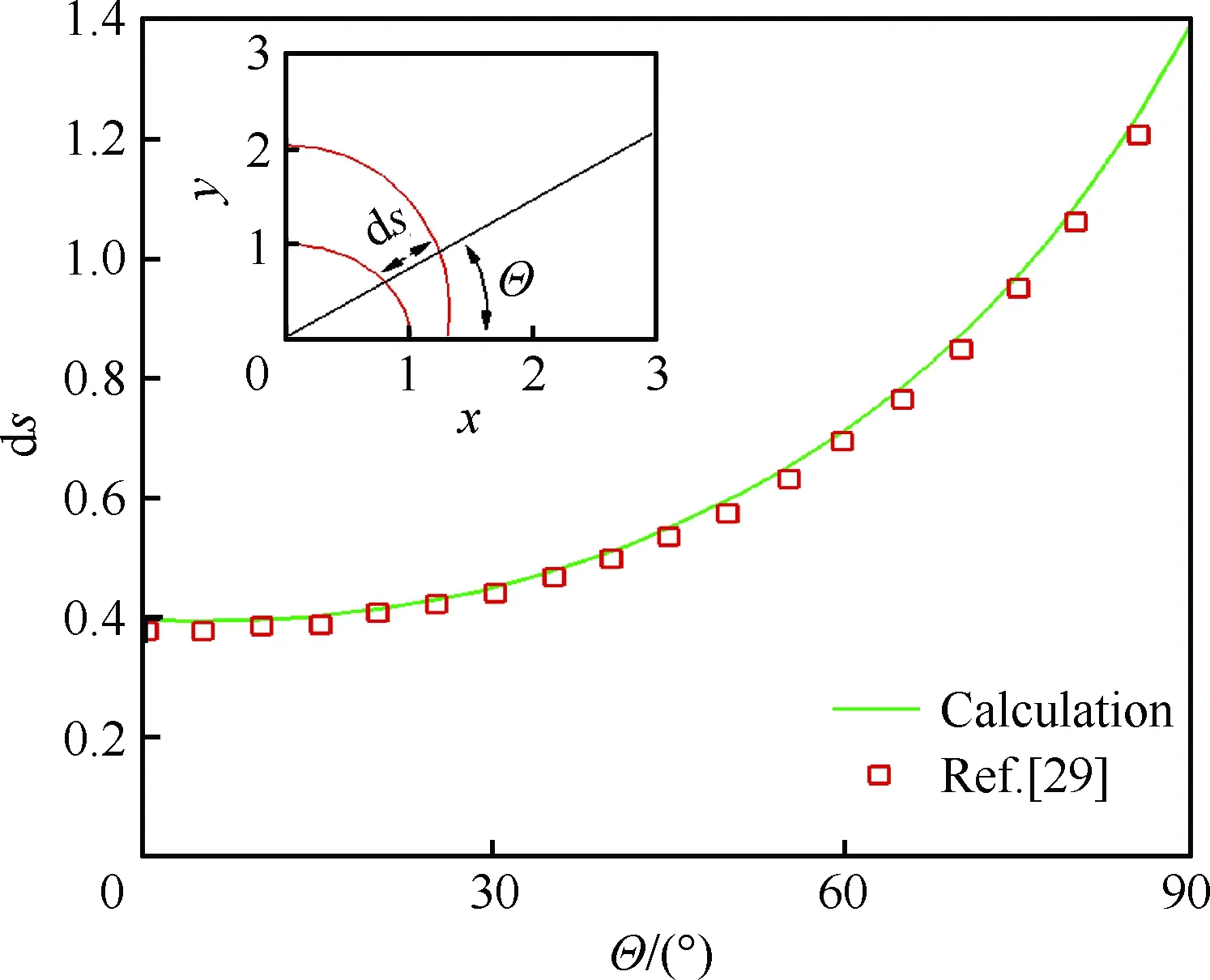
图8 激波壁面距离Fig.8 Shock wave-wall distance

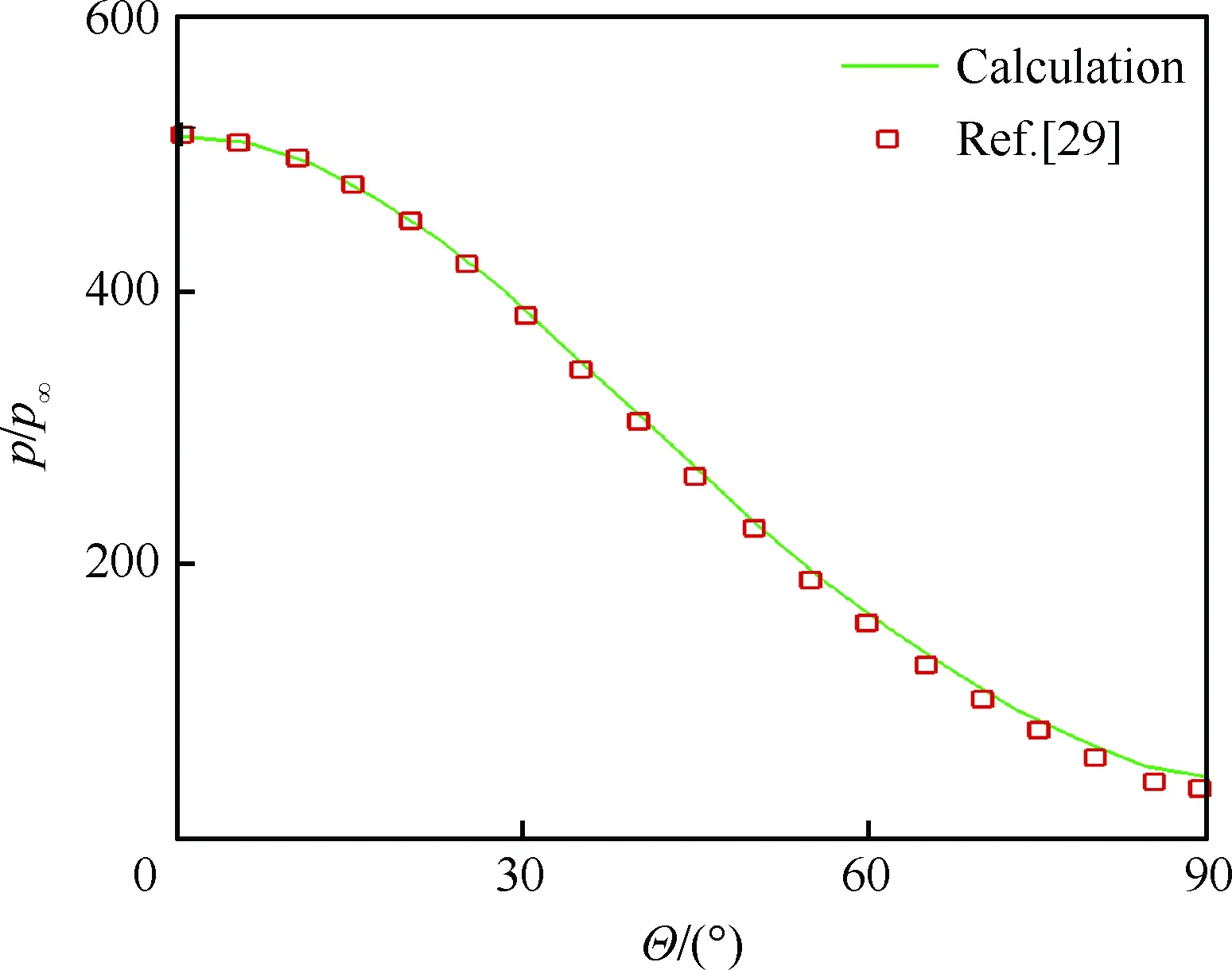
图9 归一化的壁面压力Fig.9 Normalized pressure at wall

图7给出了收敛后的马赫数云图。图8和图9分别就本文计算得到的激波到壁面距离ds和壁面压力p/p∞两个参数随角度Θ变化情况，与文献[29]进行了对比。从对比结果来看，本文中的激波装配方法获得的结果和文献中的结果吻合得较好。

总的来说，采用装配方法得到的流场结构较为清晰。由于对强激波的处理，避免了激波附近数值振荡引起整个流场的污染，所以采用很少的计算网格依然能够获得较为光滑合理的流场分布。

2.2 等截面通道内激波的运动

如图10所示，一正激波流过一等截面的通道，激波运动速度w=2.0。波前流动参数为(ρu,pu,vu)=(1.0,0.714 3,0),波后运动参数为(ρd,pd,vd)=(2.667,3.214 3,1.25)。尽管此问题是一个简单的一维问题，但是在计算过程中使用二维方式进行模拟。如图11所示，计算区域为[0,1.0]×[0,0.5]的矩形，初始激波位于x=0.25处，初始计算网格包括2 864个网格单元和1 535个网格节点。

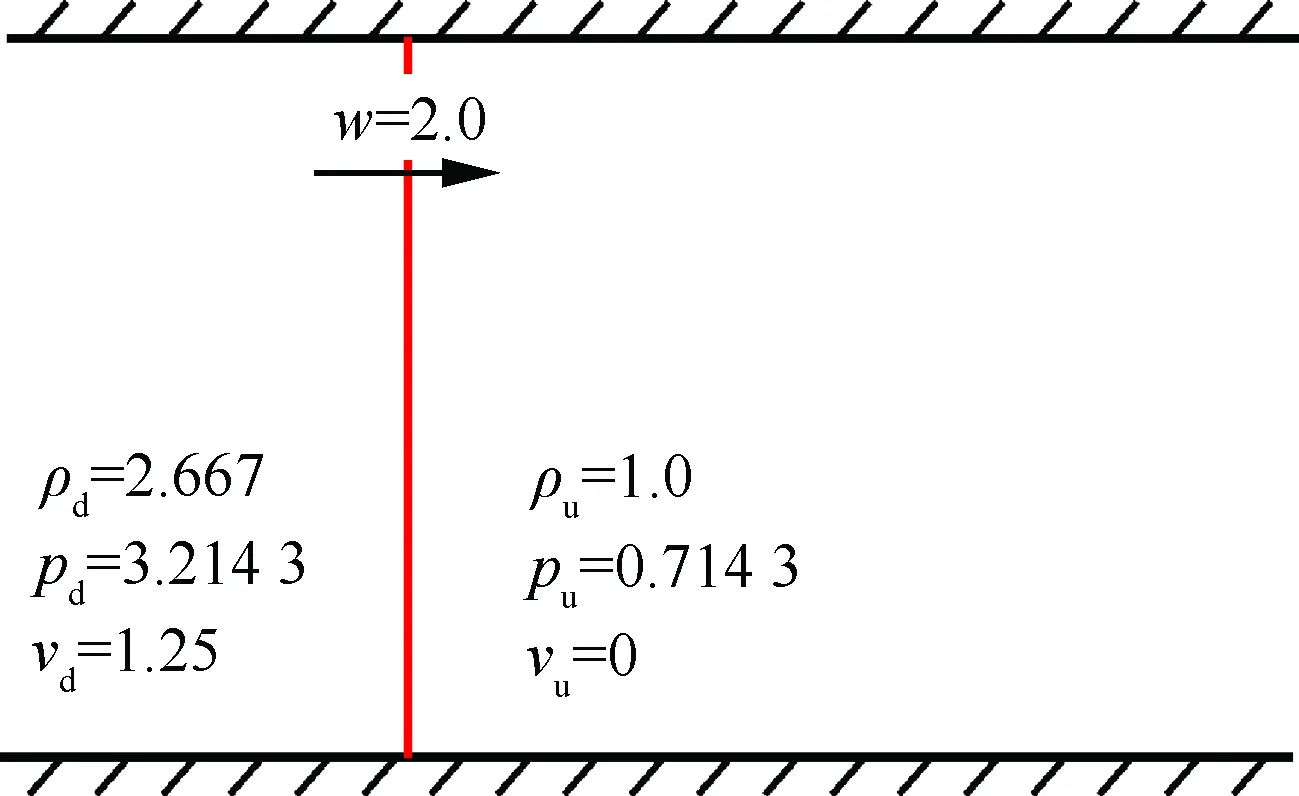
图10 流动参数设置Fig.10 Definition of flow parameters

图11 初始计算网格Fig.11 Initial computational grids

根据激波初始位置将x=0.25处的所有网格节点(共26个)标记为激波节点，由这些网格节点组成的所有面元(共25个)则被标记为激波面元。对于这些被标记为激波面元的通量按照前文所述的方法进行求解，其他的面元通量采用van Leer分裂格式求解。在计算过程中由于标记节点会进行运动，计算网格也随之发生变形。当网格质量较差时，通过重构方法来更新网格，所以计算网格数量并非完全不变。

图12给出了y=0.2时沿x方向的密度分布，其中实线表示的是t=0时刻初始流场密度分布，点划线表示的是t=0.125 5时刻的计算结果。从计算得到的密度分布可以看出：密度参数在激波处发生跳跃，激波厚度为零符合欧拉方程上描述的激波；在激波前后密度参数都为均值，没有出现任何的非物理振荡；激波从t=0时刻的初始位置x=0.25处运动到t=0.125 5时刻的x=0.5处，激波速度为w=2.0,与理论速度保持一致，这说明该方法具有足够高的计算精度。

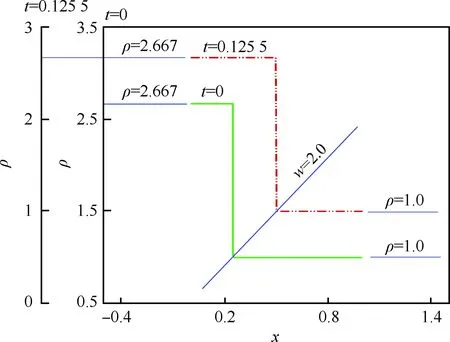
图12 沿x方向密度分布Fig.12 Density distribution along x direction

2.3 激波/涡的相互作用

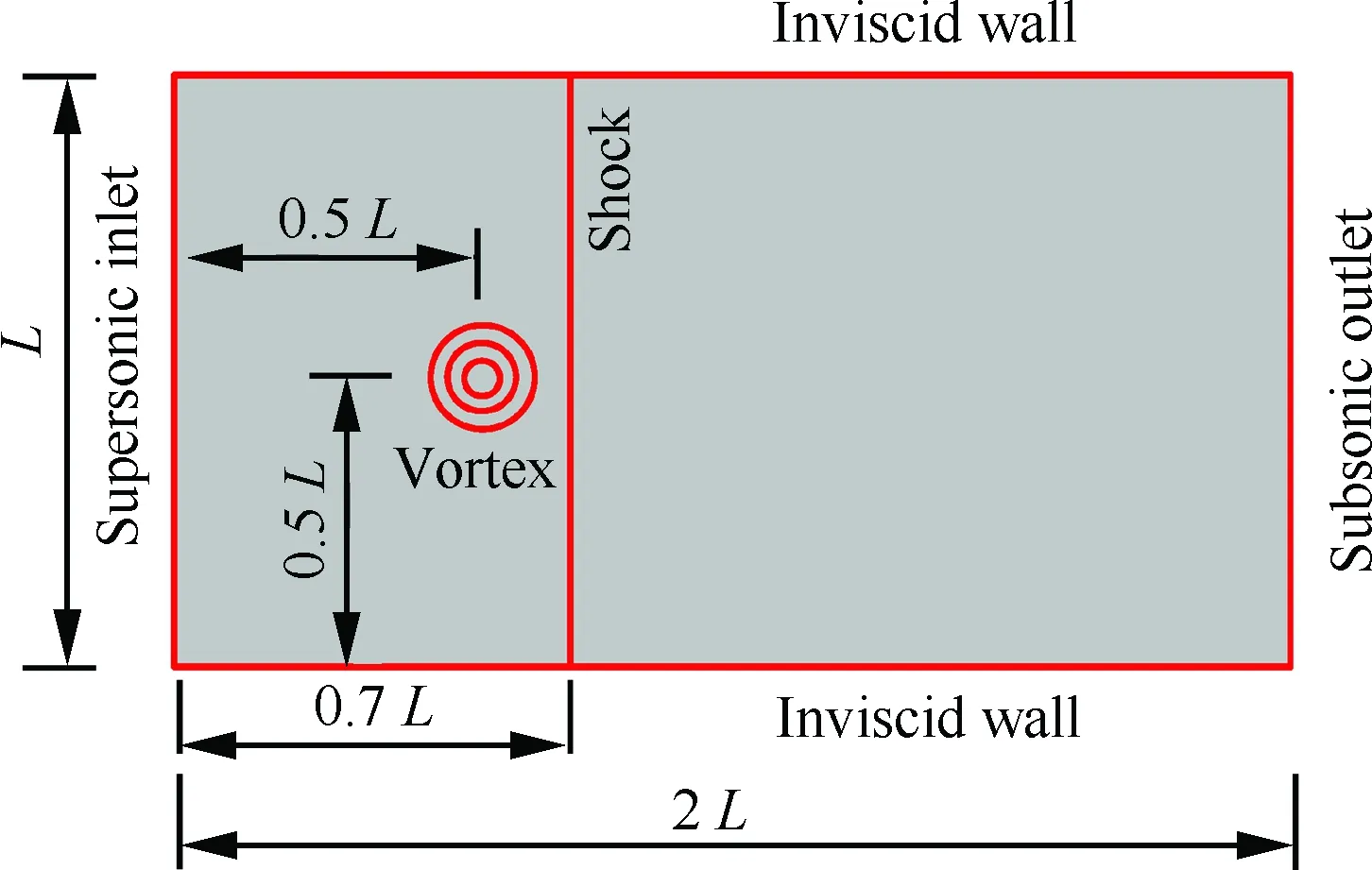
图13 计算区域和边界条件Fig.13 Computational domain and boundary conditions

考虑一个激波和涡的相互作用问题[22, 30-31]。图13给出了计算区域和相应的边界条件，其中计算区域为[0,2L]×[0,L]的矩形。在xs/L=0.7处有一个Mas=1.21的正激波。在t=0时刻，激波上游存在一个涡，涡核中心位于(xv/L,yv/L)=(0.5,0.5)处。在上游超声速流动的作用下，涡匀速向位于下游的激波方向运动，其运动速度为|u∞|。在原点位于涡核中心的极坐标下，涡只具有切向运动速度。由涡引起的速度扰动场可以表示为

(15)

式中：τ=r/rc是一个无量纲的半径参数，用来表示涡的影响范围；可以通过ε、α、rc这些参数来控制涡的形状以及影响强度。

在本算例中选择ε=0.21,α=0.204,rc/L=0.05。这样，涡的马赫数为

(16)

式中：a∞为超声速来流的声速。

激波/涡的相交问题根据激波和涡的强度进行分类。按照文献[30]中定义，对于本文中的组合而言(Mas=1.21,Mav=0.3)，会出现带有马赫反射的强相交构型出现。但是，在本文中由于缺乏相关的激波辨识模块所以只考虑主激波。

初始计算网格共由40 000个三角形单元和20 301个网格节点组成。采用两种方法对本算例进行模拟：一种是利用传统的激波捕捉方法进行模拟，面元通量全部采用van Leer分裂方法进行求解，记为S-C；另一种是对于标记的激波面元采用本文的方法计算面元通量，其他普通面元同样采用van Leer分裂格式进行求解，记为S-F。在S-F方法中，初始激波位于x/L=0.7处，所以将x/L=0.7处的网格节点标记为激波节点，对应的面元标记为激波面元。与S-C相比，由于节点的移动S-F的计算网格在计算过程中会随计算时间T发生变形，如图14所示，图中实线表示激波所在位置。

在图15中对S-C和S-F两种方法的计算结果进行了对比。从对比中可以看出，在捕捉法计算激波时需要若干网格才能描述激波，在这些网格内熵值都比较高。过激波之后，捕捉得到的流场分布较不均匀。同激波装配结果相比，沿着流动方向捕捉结果扰动影响区域更大。从图中可以看出，在捕捉激波的下游有一条形状较为规则的熵带，而在装配方法中不存在这样的熵带。通过分析， 认为这条熵带是由于捕捉激波所产生的数值误差而造成的，在激波附近产生的误差会沿着流动方向向下游传播，引起下游流场均匀性发生变化，并且没有出现衰减。由于本文中只对主激波进行了装配，对由于激波/涡相互作用产生的反射激波仍然采用捕捉方法计算，因此在激波装配结果中马赫杆下游也会出现一个较宽的激波区域，并且由于两个反射激波距离较近，捕捉得到的激波无法将两个激波分辨出来。

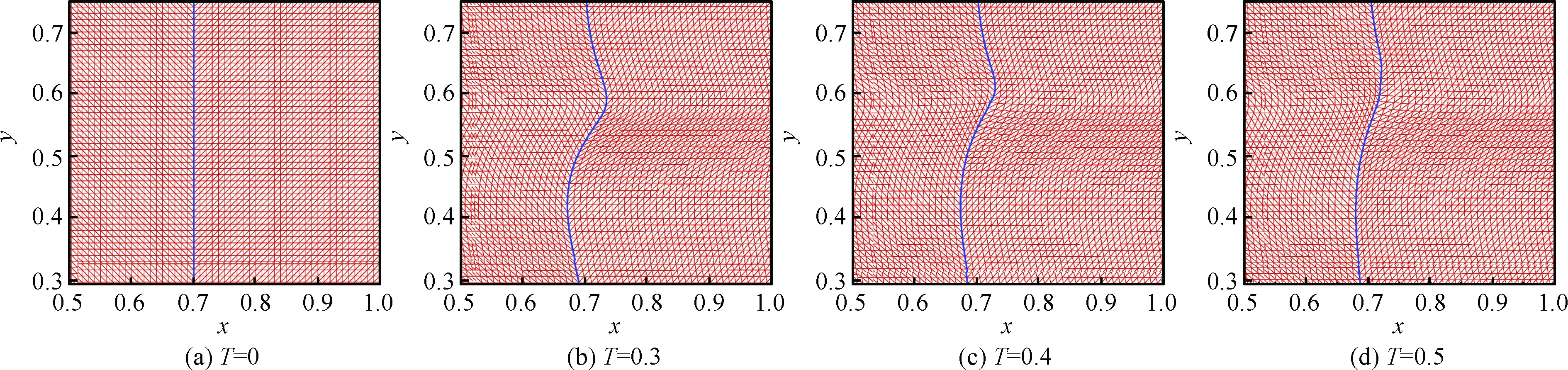
图14 激波装配法计算中随时间推进网格变形Fig.14 Grid deformations vs time evolution for shock-fitting methods

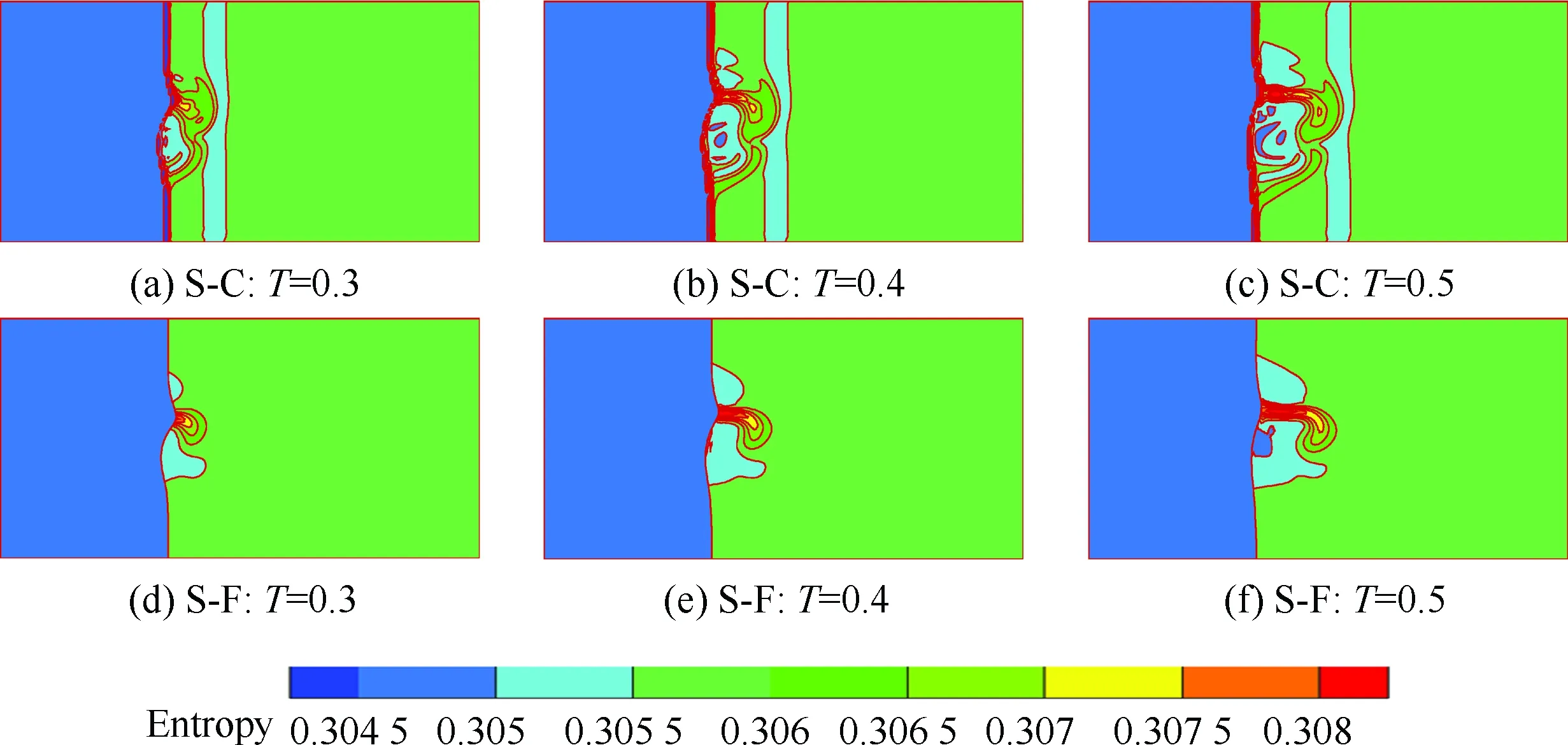
图15 S-C和S-F方法得到的不同时刻熵的云图Fig.15 Entropy iso-contours at different time instants obtained by S-C and S-F methods

3 结 论

发展了一种基于格心型有限体积法的激波装配技术。通过定义网格节点属性可以灵活调用激波装配和激波捕捉计算方法。在使用激波装配方法时，激波节点运动速度通过R-H关系式获得，同时采用非结构动网格技术描述激波的运动以及调整其他网格节点的位置。流过激波面元的通量为上游单元的基本通量，物理概念更加清晰，通量计算也更为准确。数值试验表明：本文提出的计算方法不但具有较高的计算精度，同时也能有效地避免由于捕捉激波而出现的数值问题。

[1] PIROZZOLI S. Numerical methods for high-speed flows[J]. Annual Review of Fluid Mechanics, 2011, 43(1):163-194.

[2] MORETTI G, SALAS M D. Numerical analysis of viscous one-dimensional flows[J]. Journal of Computational Physics, 1970, 5(3): 487-506.

[3] SALAS M D. Shock fitting method for complicated two-dimensional supersonic flows[J]. AIAA Journal, 1976, 14(5): 583-588.

[4] 贺国宏. 三阶ENN格式及其在高超声速黏性复杂流场求解中的应用[D]. 绵阳：中国空气动力研究与发展中心，1994： 6-11.

HE G H. Third-order ENN scheme and its application to the calculation of complex hypersonic viscous flows[D]. Mianyang: China Aerodynamics Research and Development Center, 1994: 6-11 (in Chinese).

[5] LAX P D. Hyperbolic system of conservation laws and the mathematical theory of shock waves[C]∥SIAM Regional series on Applied Mathematics, 1973.

[6] HARTEN A. High resolution schemes for hyperbolic conservative laws[J]. Journal of Computational Physics, 1983, 49(3): 357-393.

[7] OSHER S, CHAKRAVARTHY S. High resolution schemes and the entropy condition[J]. SIAM Journal on Numerical Analysis, 1984, 21(5): 955-984.

[8] CHAKRAVARTHY S, OSHER S. A new class of high accuracy TVD scheme for hyperbolic conservation laws: AIAA-1985-0363[R]. Reston, VA: AIAA, 1985.

[9] YEE H C. Upwind and symmetric shock-capturing schemes: NASA TM-89464[R]. Washington, D.C.: NASA, 1987.

[10] ROE P L. Generalized formulation of TVD Lax-Wendroff schemes: ICASE Report No. 84-53[R]. 1984.

[11] LIU X, DENG X G, MAO M L. High-order behaviors of weighted compact fifth-order nonlinear scheme[J]. AIAA Journal, 2007, 45(8): 2093-2097.

[12] QIU J X, SHU C W. On the construction, comparison and local characteristic decomposition for high order central WENO schemes[J]. Journal of Computational Physics, 2002, 183(1): 187-209.

[13] ARORA M, ROE P L. On post-shock oscillations due to shock capturing schemes in unsteady flows[J]. Journal of Computational Physics, 1997, 130 (1): 25-40.

[14] MORETTI G. Thirty-six years of shock-fitting[J]. Computers & Fluids, 2002, 31 (4-7): 719-723.

[15] RAWAT P S, ZHONG X. On high-order shock-fitting and front-tracking schemes for numerical simulation of shock-disturbance interactions[J]. Journal of Computational Physics, 2010, 229 (19): 6744-6780.

[16] PRAKASH A, PARSONS N, WANG X, et al. High-order shock-fitting methods for direct numerical simulation of hypersonic flow with chemical and thermal nonequilibrium[J]. Journal of Computational Physics, 2011, 230 (23): 8474-8507.

[17] KOPRIVA D A. Shock-fitted multidomain solution of supersonic flows[J]. Computer Methods in Applied Mechanics & Engineering, 1999, 175 (3-4): 383-394.

[18] PACIORRI R, BONFIGLIOLI A. A shock-fitting technique for 2D unstructured grids[J]. Computers & Fluids, 2009, 38 (3): 715-726.

[19] IVANOV M S, BONFIGLIOLI A, PACIORRI R, et al. Computation of weak steady shock reflections by means of an unstructured shock-fitting solver[J]. Shock Waves, 2010, 20(4): 271-284.

[20] PACIORRI R, BONFIGLIOLI A. Shock interaction computations on unstructured, two-dimensional grids using a shock-fitting technique[J]. Journal of Computational Physics, 2011, 230(8): 3155-3177.

[21] BONFIGLIOLI A, GROTTADAUREA M, PACIORRI R, et al. An unstructured, three-dimensional, shock-fitting solver for hypersonic flows[J]. Computers & Fluids, 2013, 73(6): 162-174.

[22] BONFIGLIOLI A, PACIORRI R, CAMPOLI L. Unsteady shock-fitting for unstructured grids[J]. International Journal for Numerical Methods in Fluids, 2016, 81(4): 245-261.

[23] MORETTI G, ABBETT M. A time-dependent computational method for blunt body flows[J]. AIAA Journal, 1966, 4(12): 2136-2141.

[24] 刘君， 邹东阳， 徐春光. 基于非结构动网格的非定常激波装配方法[J]. 空气动力学学报， 2015， 33(1)： 10-16.

LIU J, ZOU D Y, XU C G. An unsteady shock-fitting technique based on unstructured moving grids[J]. Acta Aerodynamica Sinica, 2015, 33(1): 10-16 (in Chinese).

[25] 刘君， 邹东阳， 董海波. 动态间断装配法模拟斜激波壁面反射[J]. 航空学报， 2016, 37(3): 836-846.

LIU J, ZOU D Y, DONG H B. A moving discontinuity fitting technique to simulate shock waves impinged on a straight wall[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(3): 836-846 (in Chinese).

[26] 刘君， 徐春光， 白晓征. 有限体积方法和非结构动网格[M]. 北京： 科学出版社， 2016.

LIU J, XU C G, BAI X Z. Finite volume methods and unstructured dynamic grids technique[M]. Beijing: Science Press, 2016 (in Chinese).

[27] BATINA J T. Unsteady Euler airfoil solutions using unstructured dynamic meshes[J]. AIAA Journal, 1990, 28(8): 1381-1388.

[28] LIU J, BAI X Z, GUO Z. A new method for transferring flow information among meshes[J]. Computational Fluid Dynamics Journal, 2007, 15(4): 509-514.

[29] LYUBIMOV A N, RUSANOV V V. Gas flow past blunt body, Part Ⅱ Table of the gasdynamic functions: NASA TT F-715[R]. Washington, D.C.: NASA, 1973.

[30] WEEKS T M, DOSANJH D S. Sound generation by shock-vortex interaction[J]. AIAA Journal, 1967, 5(4): 660-669.

[31] GRASSO F, PIROZZOLI S. Shock-wave-vortex interactions: Shock and vortex deformations, and sound production[J]. Theoretical and Computational Fluid Dynamics, 2000, 13(6): 421-456.

Applicationsofshock-fittingtechniqueforcompressibleflowincell-centeredfinitevolumemethods

ZOUDongyang1,LIUJun1, *,ZOULi2

1.SchoolofAeronauticsandAstronautics,DalianUniversityofTechnology,Dalian116024,China2.SchoolofNavalArchitectureandOceanEngineering,DalianUniversityofTechnology,Dalian116024,China

Ashock-fittingtechniqueforcell-centeredFiniteVolumeMethod(FVM)isdevelopedinthiswork.Itisflexibletoswitchamongshock-fittingandshock-capturingmethodsbychangingthenatureofgridnodes,whicharedefinedasshocknatureandcommonnature.Intheshock-fittingmethod,velocitiesofshocknodesanddownstreamstatesareobtainedbysolvingRankine-Hugoniot(R-H)relations.Theunstructureddynamicgridtechniqueisusedforshocktrackingandupdatingthepositionsofothercommonnodes.Thefluxacrossashockfaceequalsthebasicfluxofitsupstreamcell.Duringthecomputationalprocess,thenatureofthenodesisallowedtochange.Thus,itiseasiertoapplythismethodincomplexproblems,evenwithtopologicalchange.Thenumericalresultsshowtheproposedmethodisnotonlyofhighaccuracy,butalsoabletoavoidthetroublesinshock-capturing.

shock-fitting;unstructureddynamicgrid;FiniteVolumeMethod(FVM);computationalfluiddynamics;compressibleflow

2017-04-27；Revised2017-06-09；Accepted2017-06-19；Publishedonline2017-06-260907

URL：http://hkxb.buaa.edu.cn/CN/html/20171113.html

NationalNaturalScienceFoundationofChina(91541117)

.E-mailliujun65@dlut.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121363

V211；O354.5

A

1000-6893(2017)11-121363-11

2017-04-27；退修日期2017-06-09；录用日期2017-06-19；< class="emphasis_bold">网络出版时间

时间：2017-06-260907

http://hkxb.buaa.edu.cn/CN/html/20171113.html

国家自然科学基金(91541117)

.E-mailliujun65@dlut.edu.cn

邹东阳，刘君，邹丽．可压缩流动激波装配在格心型有限体积法中的应用J． 航空学报,2017,38(11):121363.ZOUDY,LIUJ,ZOUL.Applicationsofshock-fittingtechniqueforcompressibleflowincell-centeredfinitevolumemethodsJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):121363.

(责任编辑：李明敏)