考虑机翼几何非线性的气动弹性建模与分析

郭同彪，白俊强, *，孙智伟，王晨

1.西北工业大学 航空学院，西安 710072 2.西北工业大学 无人机研究所，西安 710065

考虑机翼几何非线性的气动弹性建模与分析

郭同彪1，白俊强1, *，孙智伟2，王晨1

1.西北工业大学 航空学院，西安 710072 2.西北工业大学 无人机研究所，西安 710065

大展弦比柔性机翼结构重量轻、气动效率高，广泛应用于高空长航时无人机(UAVs)。飞行过程中，这类机翼在气动力作用下发生大变形，线性结构模型不再适用，需要建立考虑几何大变形的结构模型。采用牛顿力学方法推导了考虑结构几何非线性的机翼结构动力学模型，该方法推导过程简洁、物理意义明确，可以与Hodges基于哈密顿原理的推导方法相互补充，相互验证。为了能够更准确地求解大展弦比柔性机翼的非定常气动力，建立了能够考虑机翼三维效应且适用于机翼空间大变形的非定常气动力模型。基于建立的非线性结构模型和非定常气动力模型，采用松耦合方法建立了非线性气动弹性模型，并通过算例验证了气弹模型的准确性。研究结果表明，大展弦比柔性机翼颤振速度对来流迎角和机翼的展长均较为敏感；当来流速度大于颤振速度时，由于几何非线性，机翼振动并未发散而是形成稳定的极限环振荡(LCO)；随着来流速度进一步增加，机翼再次穿过临界稳定点，由不稳定系统变为稳定系统，直到随着速度的增加系统再次达到临界稳定状态。

非线性气动弹性；几何非线性；柔性机翼；颤振速度；极限环振荡；时域响应

高空长航时无人机在情报、侦查、监视等军用领域以及环境监测、通信中继、气象等民用领域，有着广阔的应用前景，近年来在世界各国得到了广泛的发展。为了减轻结构重量、提高升阻比，高空长航时无人机普遍采用大展弦比柔性机翼[1]。在飞行过程中特别是受到大气紊流扰动的情况下，这类机翼产生较大的弯曲和扭转变形，对结构固有模态和动力学特性有着较大的影响。文献[2]指出，机翼发生大变形时其颤振速度和频率相对于未变形状态变化可高达50%，此时基于小变形假设的线性结构模型无法满足精度要求，需要建立考虑几何非线性的结构模型[2-4]。

Hodges建立的几何非线性梁动力学模型[5]，能够考虑任意大位移/转动和横向剪切变形，被广泛应用于大展弦比柔性机翼的结构建模[2,6-8]。Hodges基于哈密顿原理推导梁动力学模型，该方法无需对梁进行受力分析，不足之处在于推导过程比较繁琐，且物理意义不明确，这也是分析力学方法建立动力学方程的固有缺陷。本文采用经典的牛顿方法推导了几何非线性梁模型，该方法推导过程简洁，物理意义明确，可以与Hodges的推导方法相互补充，具有一定的理论意义。

相比于传统刚度较大的机翼，大展弦比柔性机翼的气动弹性设计更具有挑战性[1]，其在气动力作用下易发生几何大变形，并受大变形影响，发生气动失速[4]。这类机翼的设计难点主要在于几何大变形，以及由此引发的结构几何非线性和气动力非线性。

在静气弹方面，由于几何大变形，机翼气动载荷分布[9-10]、配平迎角[11-12]等均发生了显著的变化，在设计初期必须考虑大变形带来的影响。

相比于静气弹，大展弦比柔性机翼的动气动弹性问题更加复杂，近年来吸引了大批研究者。文献[6]指出，对于大展弦比柔性机翼，即使来流速度小于颤振速度，在较大的初始扰动作用下，机翼振荡也可能不收敛，表现为等幅振荡。多个学者的研究结果表明[6-7,13-15]，当来流速度大于颤振速度时，大变形引起的几何刚化效应和气动分离诱导机翼表现为有限幅值的极限环振荡(LCO)，而非一直发散；而且当不考虑气动非线性时，仅考虑几何非线性也能导致机翼呈现极限环振荡[16]。

此外，各国研究者研究了结构几何参数和来流迎角对大展弦比柔性机翼气动弹性特性的影响。Patil[8]和杨智春[17]等研究了来流迎角对机翼颤振速度和颤振频率的影响。Eskandary等[14]研究了质量比和刚度比对大展弦比机翼颤振速度和发散速度的影响。Suleman等[18]研究了机翼弦长和梢根比对大展弦比机翼时域响应的影响。以上研究中，非定常气动力模型大多采用二元翼气动力和片条理论进行建模，无法考虑气动力的三维效应。

建立能够考虑三维效应的非定常气动力模型是柔性机翼非线性气动弹性建模的一个难点。经典气弹模型中三维气动力采用偶极子网格法进行求解；当结构发生变形时，偶极子网格无法跟随结构运动形成曲面，不能准确求解机翼发生大变形时的气动载荷。杨超等[19-20]采用曲面涡格法建立了柔性机翼和飞机的气动弹性模型，它能够求解任意曲面变形机翼的气动力，且气动网格随着结构变形进行更新，适用于大变形机翼的气动弹性建模。

非定常涡格法[21](Unsteady Vortex-Lattice Method，UVLM)是一种时域非定常气动力模型，气动网格可布置成空间任意曲面形状，且可实现气动面随结构变形的自适应更新，适用于大变形机翼的定常和非定常气动力求解。本文耦合该气动力模型和结构模型建立了考虑结构几何非线性的机翼动气动弹性模型，并基于该模型研究了大展弦比柔性机翼的动气动弹性特性。

1 大展弦比机翼梁结构动力学建模

大展弦比柔性机翼在气动力作用下会发生大变形。机翼各个剖面不仅发生大的平移，还会产生较大的转动。为了准确地对机翼梁结构的变形进行描述，需引入4类坐标系(见图1)：惯性坐标系I、未变形梁截面坐标系b、变形梁截面坐标系B以及机翼随体坐标系A。

未变形梁、变形梁的参考线和横截面如图2所示，本文在推导动力学方程时以刚心轴作为梁的参考线。x1为沿未变形梁参考线的曲线坐标，s为沿变形梁参考线的曲线坐标，且s=s(x1)。未变形梁参考线上任一点在惯性系下的位置矢量用r(x1)表示，位移矢量用u(x1)表示，则变形梁参考线上该点在惯性系下的位置矢量R(x1)=r(x1)+u(x1)。根据坐标系的定义可知，未变形梁参考线的单位切线矢量为r′=b1，z′表示任意变量z对未变形梁曲线坐标x1求偏导；变形梁参考线的单位切线矢量为∂R/∂s=R′/s′,s′为基于未变形梁参考线的拉伸应变。

在考虑大变形的预扭/弯梁模型中，未变形梁曲率矢量k和变形梁曲率矢量K是两个关键的几何参数，分别表示在b坐标系和B坐标系下，即

{ki=k·bi

Ki=K·Bi

(1)

图1 本征梁模型相关的坐标系Fig.1 Coordinate system of intrinsic beam model

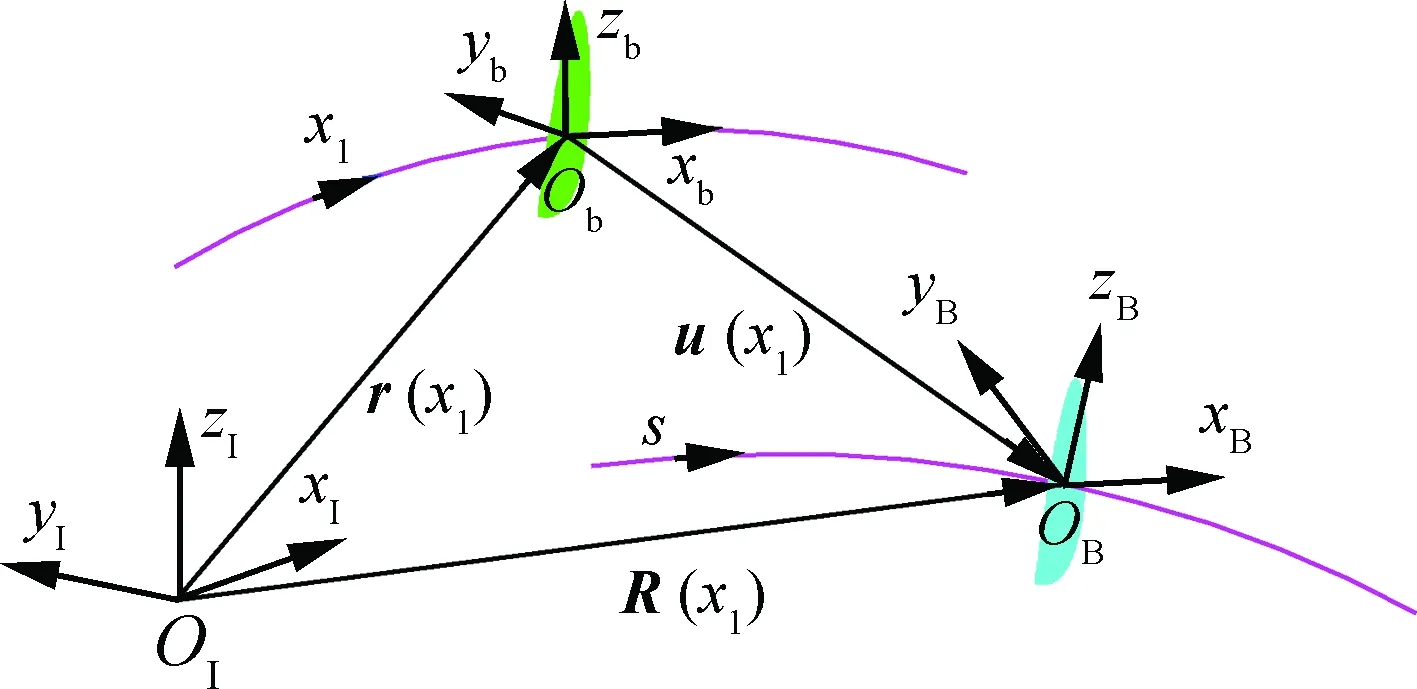
图2 本征梁变形示意图Fig.2 Schematic of deformation of intrinsic beam

式中：i=1,2,3；k1为未变形梁单位长度的扭转(即预扭)；k2和k3分别为未变形梁在b2、b3方向的曲率；K1为变形梁单位长度的扭转；K2和K3分别为变形梁在B2、B3方向的曲率。

梁截面坐标系与梁曲率矢量有如下关系[22]：

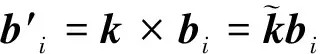
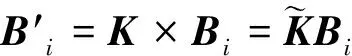
(2)

根据式(2)，任意矢量z在A坐标系和B坐标系下对x1的偏导数有如下关系：

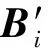
(3)

下面针对梁截面微元采用动量定理和动量矩定理推导几何非线性梁的动力学方程。图3为梁截面微元O1O2在平面内的放大示意图，其中，微元长度为dx1,T坐标系为忽略剪切变形时梁截面的局部坐标系；B坐标系基矢量和T坐标系基矢量方向的差别反映了梁剖面的剪切应变，2γ12和2γ13为剪切应变，与拉伸应变γ11构成梁的广义力应变。下面基于该梁微元对梁进行受力分析，并建立梁的动力学方程。

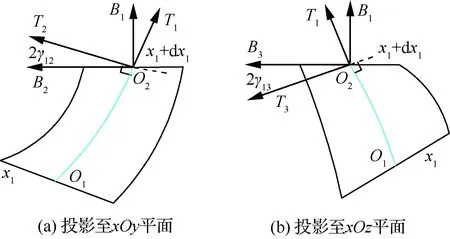
图3 梁微元变形放大示意图Fig.3 Schematic of infinitesimal deformation of beam

1.1 基于动量定理推导几何非线性梁的动力学方程

设微元左端受到的弹性力为F(x1)，则在右端受到的弹性力可表示为

(4)

则单位长度梁元受到的弹性合力为

(5)

令梁横截面内任意质点P在局部坐标系B内的位置矢量为

ξP=[0xP2xP3]

(6)

则该质点的速度矢量为

VP=VB+Ω×ξP

(7)

式中：VB为梁截面B坐标系原点的速度；Ω为梁截面的角速度矢量。

单位长度梁元的线动量为

μ(VB+Ω×ξcg)

(8)

式中：ξcg为梁截面质心的位置矢量；μ为单位长度梁元的质量。

单位长度梁元的线动量对时间的导数为

I(dP/dt)=B(dP/dt)+Ω×P

(9)

根据动量定理，质点系的动量对时间的导数等于作用在该质点系的所有外力的矢量和，即

(10)

1.2 基于动量定理推导几何非线性梁的力矩方程

设微元左端的弹性力矩为M(x1)，则在右端的弹性力矩可表示为

M(x1+dx1)=M(x1)+A(∂M/∂x1)dx1=

(11)

则单位长度梁元受到的弹性合力矩为

(12)

[(1 +γ11) 2γ122γ13]Tdx1=(e1+γB)dx1

(13)

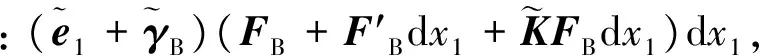
单位长度梁元对惯性系原点OI的动量矩为

(14)

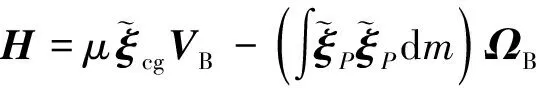
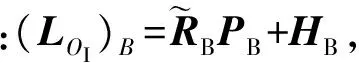
(15)

根据动量矩定理可知，质点系对固定点的动量矩对时间的导数等于作用在该质点系的所有外力对同一点的矩的矢量和，则

(16)

将式(10)代入式(16)，得到

(17)

式(17)即描述梁转动的动力学方程。至此完成了几何非线性梁动力学方程的推导。将平动和转动动力学方程统一表示为

(18)

(19)

可以看出，以上推导具有以下几个特点：① 推导过程十分简洁、直观；② 直接得到了动力学方程的强形式；③ 动力学方程中每一项物理意义明确。

1.3 结构动力学方程的空间离散

几何非线性梁的动力学方程是对时间和空间求导的偏微分方程组，求解困难。为了便于求解，采用有限元方法进行空间离散，将偏微分方程组转化为时间坐标的常微分方程组。选取R(s)(见图2)和Ψ(s)(从A坐标系到B坐标系的笛卡儿旋转矢量)作为结构状态变量[23]。第n个有限元内任意点的结构状态变量为

(20)

式中：Ni(s)为形函数，sn-1≤s≤sn。令η为所有有限元节点的位置和旋转矢量，则对机翼结构动力学方程进行有限元离散后表述为

(21)

式中：M为切线质量矩阵(Tangent Mass Matrix)；Qgyr、Qstiff、Qext分别为回转力、弹性力和外力，详细推导过程见文献[23]。

2 大展弦比柔性机翼气动力求解

本文采用非定常涡格法(UVLM)计算大展弦比柔性机翼的气动力。该算法在每个离散时间步处理翼面网格和尾迹网格的运动以及附着涡和尾迹涡的变化，适用于大变形机翼气动力求解。非定常涡格法的求解流程如图4所示。

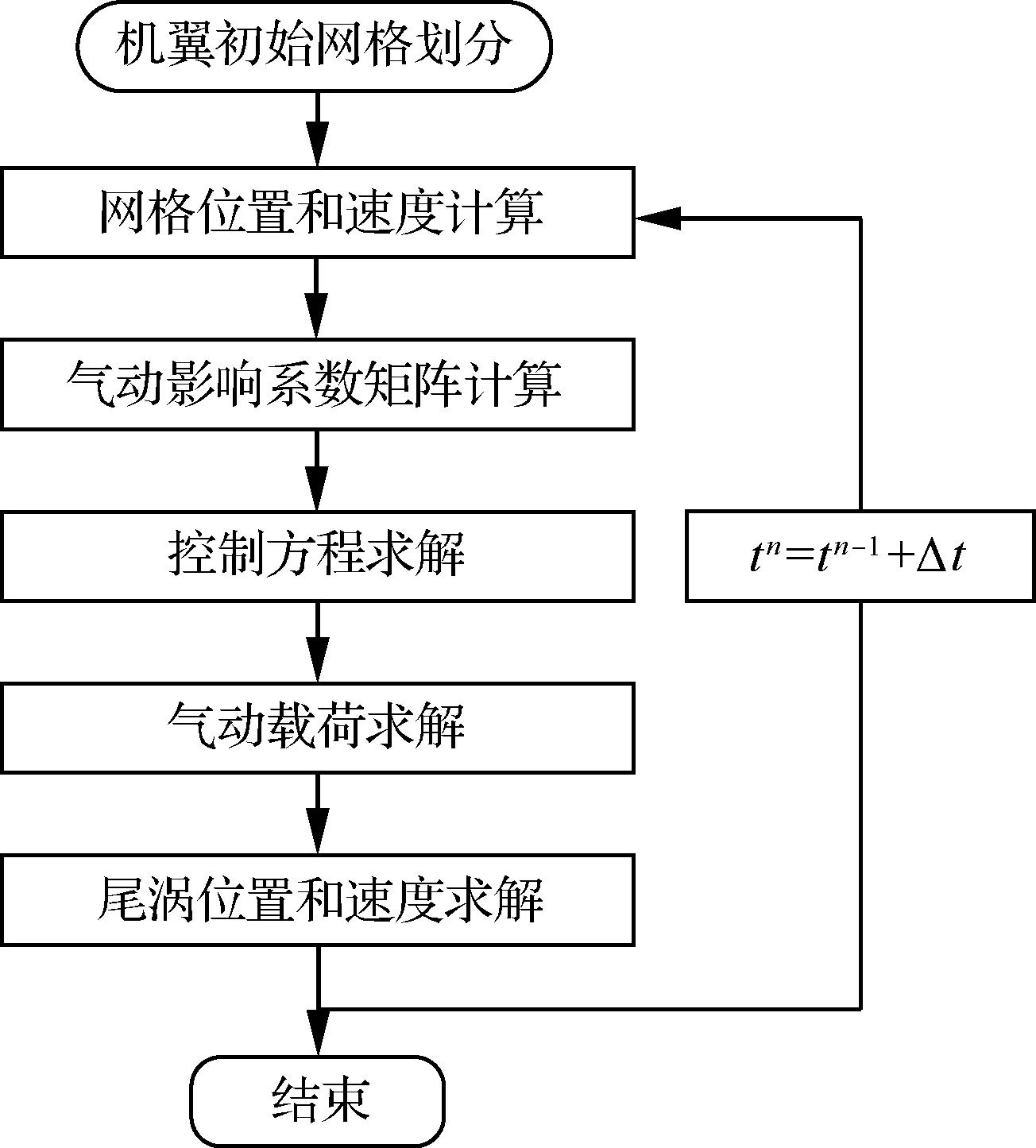
图4 非定常涡格法计算流程Fig.4 Flow chart for unsteady vortex-lattice method calculation

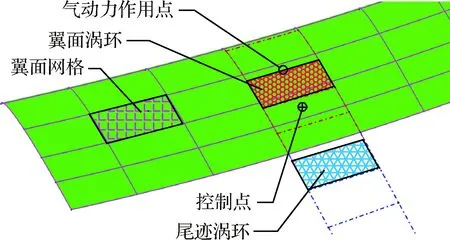
图5 涡格划分示意图Fig.5 Schematics of vortex lattice discretization

图5为涡格法机翼网格划分示意图。与偶极子格网法类似，翼面涡环的前缘线布置在翼面网格的1/4弦线；涡环前缘线中点为气动力作用点；控制点布置在翼面网格3/4弦线中点，在该点满足无穿透边界条件。

设翼面涡环数为N=ncnb(nc和nb分别为沿弦向和展向的网格数)，尾迹涡环数为M=nwnb(nw为沿弦向的网格数)。对于强迫振动，各个网格点的位移和速度为时间的函数，可以直接求解；对于气动弹性问题，网格点的位移和速度通过结构动力学模型求解得到。通过在各个翼面网格的控制点(Collocation Point)处满足无穿透边界条件建立非定常涡格法的控制方程，则各控制点处法向洗流速度vn与翼面涡强度γb和尾涡γw之间的关系为

(22)

即

AΓb=vn-BΓw

(23)

式中：A和B分别为翼面涡环和尾迹涡环的气动力影响矩阵；Γb和Γw分别为翼面涡强度和尾迹涡强度；aij为第j个翼面涡环的单位涡强度在第i个翼面涡环控制点的诱导速度；bik为第k个尾迹涡环的单位涡强度在第i个翼面涡环控制点的诱导速度。在每一步时间推进求解中，根据翼面网格的变形量和速度更新A和vn。 尾迹涡环的涡强Γw是各个时刻机翼后缘涡脱落而产生的，且根据卡尔文环量定理，t+1时刻翼面邻近的尾迹涡环的强度与t时刻翼面后缘处涡环的强度相等。因此，Γw可表示为

(24)

式中：Cb和Cw为常数矩阵。求解矩阵B的关键在于计算尾迹涡环的位置，该过程计算较为复杂，详细过程可参考文献[22]。

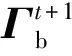
3 气动弹性模型

基于机翼结构非线性动力学模型和非定常气动力模型，采用松耦合的方法建立大展弦比柔性机翼的非线性气动弹性模型。耦合的难点在于气动和结构之间的插值，即结构位移和速度插值到翼面涡环的节点，气动力插值到结构有限元节点上，但对于梁结构模型，该过程很容易实现。图6为气动网格和结构有限元离散示意图。

在大展弦比柔性机翼的结构建模中，假设机翼剖面是刚性的，即同一机翼剖面各点的相对位置保持不变。通过结构动力学方程，可以求解弹性轴上各点的位置和速度，进而通过式(6)和式(7)可求解翼面任意点的位移和速度。同时，作用在翼面的气动载荷可以直接通过虚功原理转换至结构有限元节点上。

本文采用Newmark-β方法对非线性动力学方程进行时域推进求解，非线性结构动力学方程采用Newton-Raphson方法迭代求解，且为了提高求解效率，在动力学方程求解中，不对气动力进行更新，具体求解过程见图7。为了弥补这种松耦合求解方法带来的精度损失，本文在时域响应推进求解中采用较小的时间步长。

图6 气动网格和结构有限元离散示意图Fig.6 Schematic of aerodynamic panels and structure finite element discretization

图7 非线性气动弹性时域响应流程Fig.7 Flow chart for nonlinear aeroelasticity time marching response

4 模型验证与算例

Patil和Hodges采用的机翼[2]被广泛应用于考虑几何非线性的非线性气动弹性特性研究中，机翼的几何和结构参数如表1所示，平面形状如图8所示。机翼结构模型和气动模型沿展向采用相同的划分方式，有限元个数为24个，气动网格沿弦向布置8个，其中大气密度为0.088 9 kg/m3。

表1 机翼几何和结构参数Table 1 Geometry and structure parameters of wing

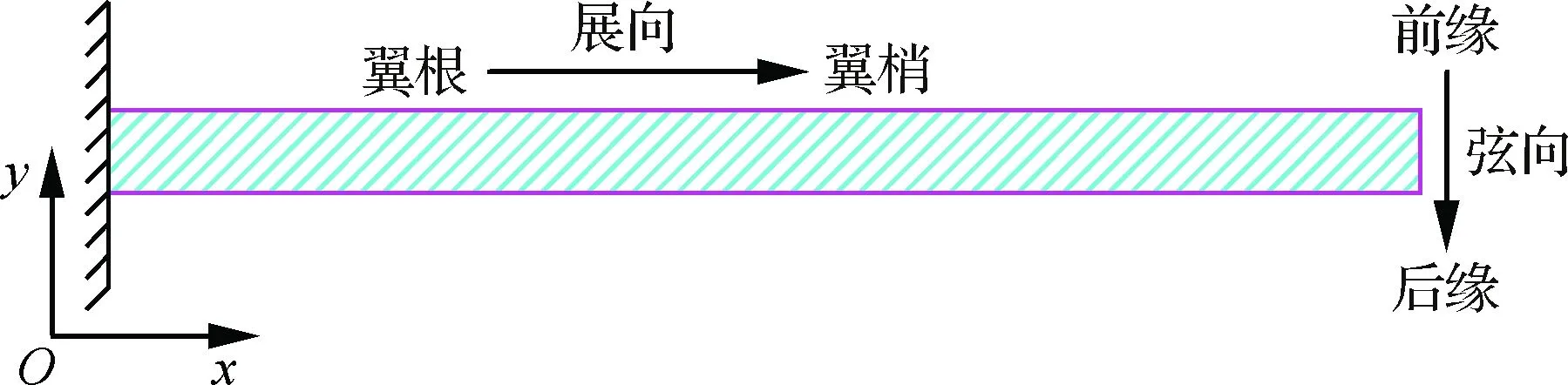
图8 悬臂机翼示意图Fig.8 Schematics of cantilever wing

4.1 大展弦比柔性机翼颤振速度求解

本文采用时域仿真的方法求解颤振速度。在给定迎角下，逐渐增加来流速度，在静气弹平衡位置的基础上给机翼一个小扰动(0.02°迎角)，进行时域仿真，通过观察机翼是否呈等幅振荡判断其是否达到临界颤振速度。

图9为翼根迎角为3°时，不同来流速度U∞下机翼翼梢扭转角度的时域响应对比图，从图中可以看出，来流速度U∞=23.7 m/s时，随着时间的推进振荡振幅减小，逐渐收敛；来流速度U∞=24.8 m/s时，随着时间的推进振幅增加，逐渐发散；来流速度U∞=24.2 m/s时，为等幅振荡。因此颤振速度为24.2 m/s(在求解时，进行了不同速度下大量的时域仿真计算，以保证该速度为呈现等幅振荡的最小速度)。

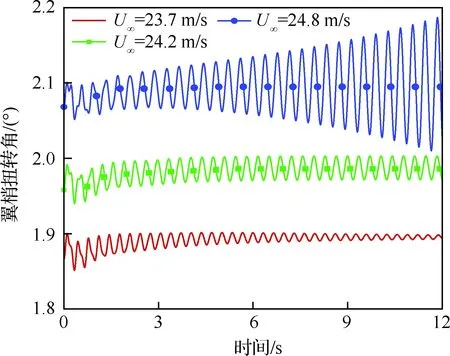
图9 3°翼根迎角时不同来流速度翼梢扭转的时域响应Fig. 9 Time history of tip twist at various free-stream speeds for root angle of attack=3°

图10 不同翼根迎角下的颤振速度Fig.10 Flutter speed at various root angles of attack

图10为根据上述准则求解的机翼颤振速度随机翼迎角的变化曲线，从图中可以看出，本文计算结果与文献[17]基本相同，与文献[8]趋势一致，但有一个约2 m/s的差量，差量主要是因为文献采用的气动力模型是基于片条理论的二元机翼有限状态气动力模型，无法考虑机翼的三维效应，计算的气动力偏大，使得其计算的颤振速度偏小。

4.2 来流迎角和机翼展长对颤振速度的影响

展长是决定机翼柔性大小的关键参数，主导着飞行过程中机翼产生大变形的程度。从4.1节可以看出，来流迎角对颤振速度也有明显的影响。本节将进一步探索这两个参数对颤振速度的影响。其余各个参数与表1相同。

图11为不同机翼展长在不同翼根迎角下的颤振速度变化图。从图中可以看出，对于不同展长的机翼，随着迎角的增加，颤振速度逐渐减小，但减缓的速率越来越小，来流迎角从1°增加至3°时，颤振速度降低约20%，可见大展弦比柔性机翼的颤振速度对来流迎角较为敏感。

图11 不同翼根迎角和展长机翼的颤振速度Fig.11 Flutter speed at various root angles of attack with different span-wise lengths

随着机翼展长的增加，机翼的颤振速度也有明显的变化，不同迎角下，颤振速度均逐渐减小，不过减缓速率也逐渐减小，机翼半展长由12 m增加至18 m时，颤振速度降低约30%。从气动的角度来说，增加展长可以减小诱导阻力，进而提高升阻比，但机翼的气动弹性特性恶化，在设计时应综合考虑。

4.3 非线性气动弹性时域响应特性

对于线性气动弹性模型，当来流速度大于颤振速度时，机翼运动的振幅随着时间呈指数形式增加；当考虑到非线性后，将呈现更复杂的响应。本节将研究在初始小扰动条件下(0.02°来流迎角)，来流速度大于颤振速度时，大展弦比柔性机翼的时域响应特性。

图12为3°迎角下，来流速度大于机翼颤振速度24.2 m/s时，翼梢扭转角位移的时域响应。从图12可以看到，在初始阶段，响应振幅逐渐增加，而后机翼运动收敛至稳定的极限环振荡。关于机翼运动没有持续发散的原因，文献[6-7,13-16]将其归因于结构几何非线性或者气动非线性，但并未进一步深入分析。本文接下来对极限环产生原因进行简要叙述。

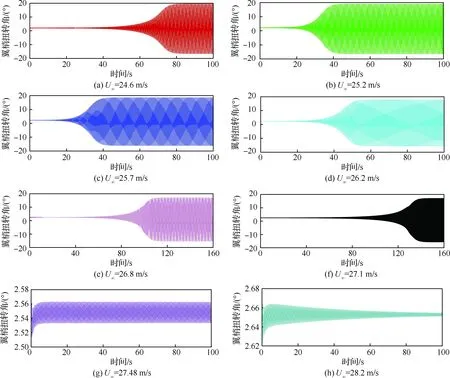
图12 3°翼根迎角不同来流速度下翼梢扭转角的时域响应Fig.12 Time history of tip twist at various free-stream speeds for 3° root angle of attack

另一方面，当变形较大时，机翼展向长度减小，且剖面方向也发生变化，使得相同迎角下机翼的升力和力矩也减小。以翼根迎角为3°、来流速度为25.7 m/s时，75%展向位置处剖面俯仰力矩非线性为例进行分析。图13给出了在20 s和60 s 附近一个周期内剖面俯仰力矩随扭转角的变化曲线。在20 s时，剖面扭转角度振动范围较小，大变形效应不明显，力矩线性特性较好；在60 s 时，扭转角振动范围较大，由于大变形效应，在0°扭转角增加至最大扭转角过程中，有明显的力矩损失，该非线性效应减小了扭转角增加的趋势，有利于维持机翼的等幅振荡。

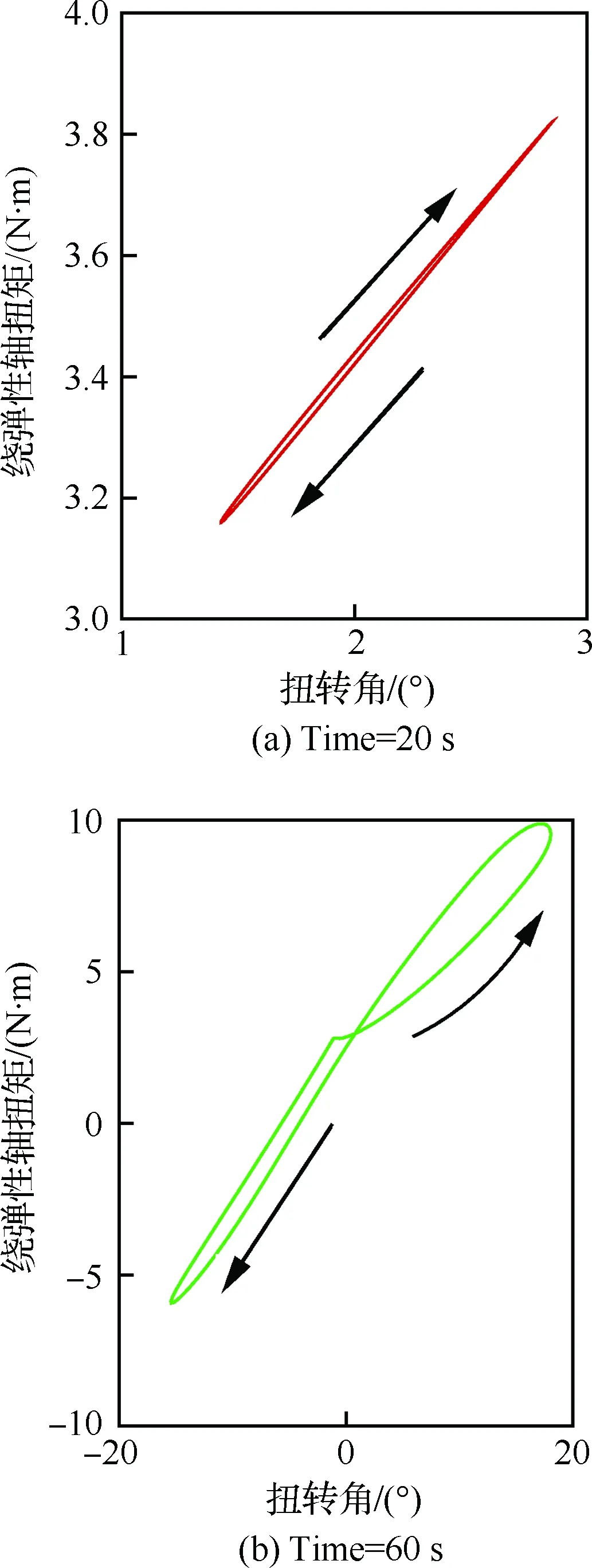
图13 3°翼根迎角、U∞=25.7 m/s时，75%展向位置 处剖面扭转力矩随扭转角的变化曲线Fig.13 Section moments of torque curves for U∞=25.7 m/s in 75% spanwise position with respect to twist angle for 3° root angle of attack

图14给出了3°来流迎角不同来流速度下，机翼翼梢扭转角的幅值变化。随着来流速度的增加，机翼在平衡位置附近小幅振荡发散的速率先增加后减小；在线性气弹系统中，振动发散的速率和系统的阻尼正相关，系统的阻尼越大，发散的速率越大；而机翼在平衡位置附近小幅振荡范围内，机翼几何非线性效应较弱，因此可以认为气动弹性系统在平衡位置处的阻尼也先增加后减小，这和文献[9]采用几何非线性梁和二元非定常气动力模型计算结果的趋势相同。从图12(g)可以看出，当来流速度为27.48 m/s时，机翼在平衡位置附近维持小振幅振荡，而非先发散后维持极限环振荡，可见此时系统处于临界稳定状态，系统由不稳定变为稳定。随着速度进一步增加，系统的振荡收敛(图12(h))。

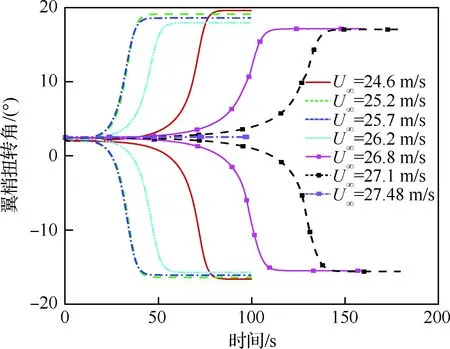
图14 3°翼根迎角不同来流速度下翼梢扭转角的幅值 Fig.14 Amplitude of tip twist at various free-stream speeds for 3° root angle of attack

综上可以看出，来流速度增加至24.2 m/s时，机翼由收敛运动变为静平衡位置附近的小幅振荡运动，系统的阻尼由负变为0，处于临界稳定状态； 随着来流速度进一步增加，系统阻尼为正，机翼在静平衡位置附近呈现发散振荡，且发散率先增加后减小；直到来流速度为27.48 m/s时，系统发散率减小至0，机翼在静平衡位置附近小幅振荡，系统再次处于临界稳定状态；随着来流速度进一步增加，系统表现为收敛振荡运动，直到速度增加至39.4 m/s时，系统第3次达到临界稳定状态(见图15)。

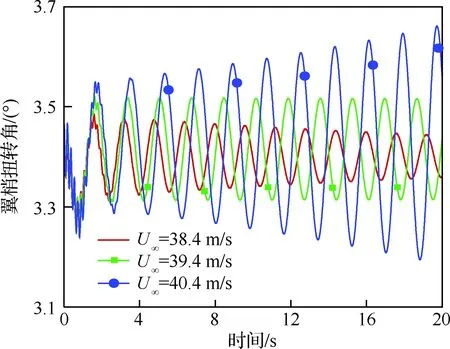
图15 3°翼根迎角不同来流速度下翼梢扭转角的 时域响应 (t=0～20 s)Fig.15 Time history of tip twist at various free-stream speeds for 3° root angle of attack (t=-20 s)

5 结 论

基于牛顿定律推导了几何非线性梁的动力学方程，与文献[5]的方法相比，推导过程简单、直观，物理意义明确，便于理解动力学方程，这也是在建立动力学方程中，牛顿力学方法相比于分析力学的优势。该方法可以与分析力学方法相互补充，相互验证。

基于机翼结构非线性动力学模型和非定常涡格法，采用松耦合的方法建立了大展弦比机翼的非线性气动弹性模型，该模型考虑了机翼大变形、非定常气动力的三维效应以及气动面随结构变形的自适应更新。

大展弦比柔性机翼的颤振特性对来流迎角较为敏感，机翼迎角由1°增加至3°时，不同展长的柔性机翼的颤振速度均降低了约20%。同时，随着机翼展长的增加，机翼的颤振速度也有明显的变化，各个迎角下，机翼半展长由12 m增至18 m时，颤振速度降低约30%。

由于结构几何非线性效应，来流速度超过颤振速度时，大展弦比柔性机翼的振动并不发散，而是呈现出稳定的极限环振荡。随着来流速度进一步增加，系统再次穿过临界平衡点(U∞=27.48 m/s)，不稳定系统变为稳定系统，直到随着速度的增加系统第3次达到临界稳定状态(U∞=39.4 m/s)。

[1] NOLL T E, ISHMAEL S D, HENWOOD B, et al. Technical findings, lessons learned, and recommendations resulting from the Helios prototype vehicle mishap[C]∥Processes and Criteria for UAV Structural Integrity, 2007.

[2] PATIL M J, HODGES D H. On the importance of aerodynamic and structural geometrical nonlinearities in aeroelastic behavior of high-aspect-ratio wings[J]. Journal of Fluids and Structures, 2004, 19(7): 905-915.

[3] TANG D M, DOWELL E H. Effects of geometric structural nonlinearity on flutter and limit cycle oscillations of high-aspect-ratio wings[J]. Journal of Fluids and Structures, 2004, 19(3): 291-306.

[4] AFONSO F，VALE J， OLIVEIRA É, et al. A review on non-linear aeroelasticity of high aspect-ratio wings[J]. Progress in Aerospace Sciences, 2017, 89: 40-57.

[5] HODGES D H. A mixed variational formulation based on exact intrinsic equations for dynamics of moving beams[J]. International Journal of Solids and Structures, 1990, 26(11): 1253-1273.

[6] PATIL M J, HODGES D H, CESNIK C E S. Limit-cycle oscillations in high-aspect-ratio wings[J]. Journal of Fluids and Structures, 2001, 15(1):107-132.

[7] XIANG J W, YAN Y J, LI D C. Recent advance in nonlinear aeroelastic analysis and control of the aircraft[J]. Chinese Journal of Aeronautics, 2014, 27(1): 12-22.

[8] PATIL M J, HODGES D H, CESNIK C E S. Nonlinear aeroelasticity and flight dynamics of high-altitude long-endurance aircraft[J]. Journal of Aircraft, 2001, 38(1): 88-94.

[9] 段静波, 周洲, 王伟, 等. 大展弦比大柔性机翼载荷分布求解的一种方法[J]. 航空学报, 2016, 37(3): 799-809.

DUAN J B, ZHOU Z, WANG W, et al. A method for aeroelastic load redistribution of very flexible wing with a high-aspect-ratio[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37 (3): 799-809 (in Chinese).

[10] 王伟, 段卓毅, 耿建中, 等. 基于CR 理论的大柔性机翼几何非线性结构建模[J]. 航空学报,2017, 38(S1):721544.

WANG W, DUAN Z Y, GENG J Z, et al. Geometrically nonlinear structural model for very flexible wing based on CR theory[J]. Acta Aeronautica et Astronautica Sinica, 2017, 38(S1): 721544(in Chinese).

[11] 杨超, 王立波, 谢长川, 等. 大变形飞机配平与飞行载荷分析方法[J]. 中国科学: 技术科学, 2012, 42(10): 1137-1147.

YANG C, WANG L B, XIE C C, et al. Aeroelastic trim and flight loads analysis of flexible aircraft with large deformations[J]. Sci China Tech Sci, 2012, 42 (10): 1137-1147 (in Chinese).

[12] WANG W, ZHU X P, ZHOU Z, et al. A method for nonlinear aeroelasticity trim and stability analysis of very flexible aircraft based on co-rotational theory[J]. Journal of Fluids and Structures, 2016, 62: 209-229.

[13] TANG D M, DOWELL E H. Experimental and theoretical study on aeroelastic response of high-aspect-ratio wings[J]. AIAA Journal, 2001, 39(8): 1430-1441.

[14] ESKANDARY K, DARDEL M, PASHAEI M H, et al. Nonlinear aeroelastic analysis of high-aspect-ratio wings in low subsonic flow[J]. Acta Astronautica, 2012, 70(1): 6-22.

[15] ARENA A, LACARBONARA W, MARZOCCA P. Nonlinear aeroelastic formulation and postflutter analysis of flexible high-aspect-ratio wings[J]. Journal of Aircraft, 2013, 50(6): 1748-1764.

[16] SHAMS S, SADR M H, HADDADPOUR H. An efficient method for nonlinear aeroelasticy of slender wings[J]. Nonlinear Dynamics, 2012, 67(1): 659-681.

[17] 杨智春, 张惠, 谷迎松, 等. 考虑几何非线性效应的大展弦比机翼气动弹性分析[J]. 振动与冲击, 2014,33(16): 72-75.

YANG Z C, ZHANG H, GU Y S, et al. Aeroelastic analysis of the high aspect ratio wing considering the geometric nonlinearity[J]. Journal of Vibration and Shock, 2014, 33(16): 72-75 (in Chinese).

[18] SULEMAN A, AFONSO F, VALE J, et al. Non-linear aeroelastic analysis in the time domain of high-aspect-ratio wings: Effect of chord and taper-ratio variation[J]. Aeronautical Journal, 2017, 121(1235): 21-52.

[19] 谢长川, 胡锐, 王斐, 等. 大展弦比柔性机翼气动弹性风洞模型设计与试验验证[J]. 工程力学, 2016, 33(11): 249-256.

XIE C C, HU R, WANG F, et al. Aeroelastic wind tunnel test model design and experiment on very flexible high-aspect-ratio wings[J]. Engineering Mechanics, 2016, 33 (11): 249-256 (in Chinese).

[20] LIU Y, XIE C C, YANG C, et al. Gust response analysis and wind tunnel test for a high-aspect ratio wing[J]. Chinese Journal of Aeronautics, 2016, 29(1): 91-103.

[21] KATZ J, PLOTKIN A. Low-speed aerodynamics[M]. Cambridge: Cambridge University Press, 2001.

[22] HODGES D H. Nonlinear composite beam theory[M]. Reston, VA: AIAA, 2006.

[23] GÉRADIN M, CARDONA A. Flexible multibody dynamics: A finite element approach[M]. Chichester: Wiley, 2001.

Aeroelasticmodelingandanalysisofwingsconsideringgeometricnonlinearity

GUOTongbiao1,BAIJunqiang1, *,SUNZhiwei2,WANGChen1

1.SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.UAVResearchInstitute,NorthwesternPolytechnicalUniversity,Xi’an710065,China

Flexiblewingswithhighaspectratioarewidelyusedinhigh-altitudeandlong-enduranceUnmannedAerialVehicles(UAVs)becauseoflowstructuralweightandhighaerodynamiclift-to-dragratio.Thiskindofwingsexperiencelargegeometricdeformationinflight,andthelinearstructuremodelbasedonsmalldeformationhypothesisisnolongerapplicable.Therefore,itisnecessarytobuildthestructuremodelwhichcansimulategeometricnonlinearity.BasedontheNewtonianmethod,thedynamicequationsforthegeometricnon-linearstructuremodelarederived,whichcanbemutuallyvalidatedbyandcomplementedwiththemethodbasedonHamilton’sprinciplederivedbyHodges.Tosimulatetheaerodynamicsofflexiblewingsmoreprecisely,amodelforthree-dimensionalunsteadyaerodynamics,whichcanconsiderlargedeformationofthewing,isbuilt.Basedonthenonlinearstructuremodelandtheunsteadyaerodynamicmodel,thenonlinearaeroelasticmodelisbuiltthroughloosecoupling.Theprecisionoftheaeroelasticmodelisverifiedthroughtests.Theresultsshowthattheflutterspeedofflexiblewingsissensitivetothefree-streamanglesofattackandspan-wiselength.Whenthefree-streamspeedsexceedtheflutterspeed,thewing’svibrationsarestableLimitedCycleOscillations(LCO)ratherthandivergence.However,asthefree-streamspeedscontinuesincreasing,thewing’svibrationsconvergeagainandthedampingturnedtobepositive.

nonlinearaeroelasticity;geometricnonlinearity;flexiblewing;flutterspeed;limitedcycleoscillations;timemarchingresponse

2017-04-25；Revised2017-05-15；Accepted2017-07-07；Publishedonline2017-07-121459

URL：http://hkxb.buaa.edu.cn/CN/html/20171112.html

Industry,EducationandResearchFund(cxy2014XGD09)

.E-mailjunqiang@nwpu.edu.cn

http://hkxb.buaa.edu.cnhkxb@buaa.edu.cn

10.7527/S1000-6893.2017.121351

V211.47

A

1000-6893(2017)11-121351-11

2017-04-25；退修日期2017-05-15；录用日期2017-07-07；< class="emphasis_bold">网络出版时间

时间：2017-07-121459

http://hkxb.buaa.edu.cn/CN/html/20171112.html

产学研基金(cxy2014XGD09)

.E-mailjunqiang@nwpu.edu.cn

郭同彪，白俊强，孙智伟，等．考虑机翼几何非线性的气动弹性建模与分析J． 航空学报,2017,38(11):121351.GUOTB,BAIJQ,SUNZW,etal.AeroelasticmodelingandanalysisofwingsconsideringgeometricnonlinearityJ.ActaAeronauticaetAstronauticaSinica,2017,38(11):121351.

(责任编辑：李明敏)