基于准Z源逆变器的光伏发电系统的双滑模变结构控制

薛 阳, 郑 蓉, 阚东跃, 时宇飞, 郑梦秋

(上海电力学院 自动化工程学院, 上海 200090)

基于准Z源逆变器的光伏发电系统的双滑模变结构控制

薛 阳, 郑 蓉, 阚东跃, 时宇飞, 郑梦秋

(上海电力学院 自动化工程学院, 上海 200090)

准Z源逆变器作为一种新型的电路拓扑结构,除了具有Z源逆变器多种优点外,还可以降低逆变器的电压电流额定值,使逆变器的输入电流更加连续.分析了双滑模变结构控制设计方式的优点.在光伏发电部分加入滑模变结构控制,能够更加快速跟踪光伏输出电压,从而达到跟踪最大功率点的目的;在光伏并网逆变器部分加入滑模变结构控制,能有效提高系统的鲁棒性和并网电能质量.最后,通过仿真模型验证了所建模型的准确性以及控制系统的有效性.

准Z源逆变器; 滑模变结构控制; 最大输出功率快速跟踪; 光伏发电

光伏并网发电系统需要解决两个技术难点:一是光伏阵列最大输出功率快速跟踪(Maximum Power Point Tracking,MPPT);二是保证单位功率因子并网,且电流总谐波畸变率低于5%,符合IEEE929—2000规定的标准[1].现代控制理论的控制策略主要包括多变量状态反馈控制,无差拍控制,滑模变结构控制,模糊控制,重复控制等[2].其中,滑模变结构控制的优点是对系统参数变化和外部扰动不敏感,具有较强的鲁棒性.由于光伏发电输出受天气影响很大,尤其在多云天气,发电功率会出现快速剧烈变化[3],因此使用滑模变结构控制能够有效地提高系统鲁棒性,提高响应速度和并网电能质量[4].

1 数学建模

准Z源逆变器作为一种新型的电路拓扑结构,与Z源逆变器相比可以降低逆变器的电压电流额定值,使逆变器的输入电流更加连续.

对于传统的三相逆变器控制,静止坐标系下的线性调节器无法消除稳态误差,目前常用的方法是通过对三相变量进行坐标变换,对转换到旋转坐标系下的直流量进行调节,从而消除稳态误差.基于以上考虑,在对准Z源逆变器的光伏发电系统进行建模时,采用的是将三相变量变换为旋转坐标系下的直流量.

1.1 光伏阵列数学模型

忽略光伏电池内阻与光伏电池的并联电阻的情况下,光伏电池的电流输出特性方程为:

(1)

式中:IPV——光伏电池的输出电流;

IL——光生伏打电流;

U——光伏电池端电压;

IO——流过二极管的反向饱和漏电流;

q——电荷量,q=1.6×10-19C;

K——玻尔兹曼常数,K=1.38×10-23J/K;

T——光伏电池的工作温度;

A——二极管的PN结面积,A=1～2 cm2.

光伏电池的输出功率为:

PPV=IPVUPV

(2)

式中:PPV——光伏电池的输出功率;

UPV——光伏电池的输出电压.

在Park坐标系下,正常运行时逆变器系统的控制方程为:

(3)

式中:P,Q——逆变器输出的有功功率与无功功率;

Ud,Uq——逆变器交流侧电压的d轴分量和q轴分量;

Id,Iq——逆变器交流侧电流的d轴分量和q轴分量.

一般认为光伏发电系统向电网输送的只是有功功率,故有:

(4)

1.2 准Z源逆变器的数学建模

假设准Z源逆变器的Z网络是对称的,即:

(5)

根据准Z源逆变器的9种开关状态——6种非零电压状态,3种零电压状态,可以将准Z源逆变器的工作模式分为以下两种.

一是直通模式.其直通状态如图1所示.

(6)

式中:UO——空载电压;

UDC——直流输出电压.

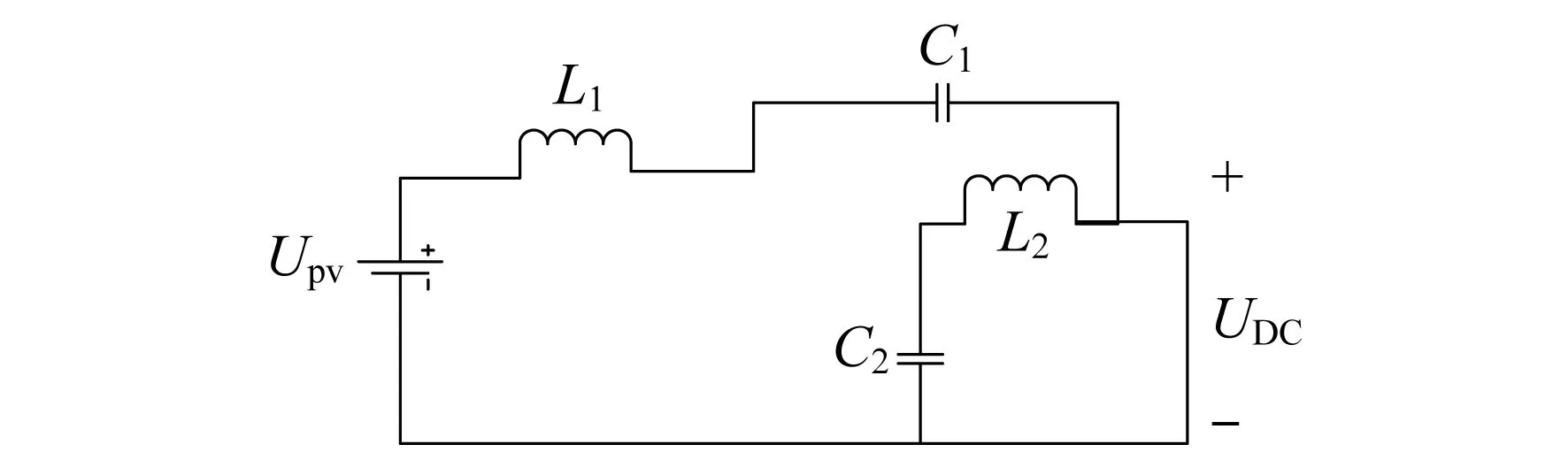
图1 直通状态示意

二是非直通模式.其直通状态如图2所示.

TS=TO+TC

式中:TS——开关周期;

TO——直通运行时间;

TC——非直通时间.

(7)

图2 非直通状态示意

由于光伏系统只向电网输送有功功率,所以在一个周期内,电感电压的平均值为零.即:

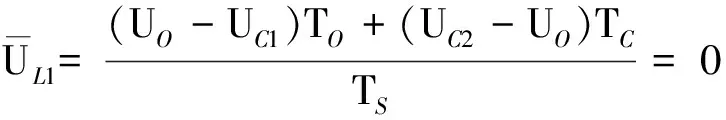
(8)

故有:

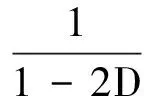
(9)

式中:D——直通占空比.

由于(1/(1-2D))>1,故准Z源逆变器具有升压能力,则逆变器输出的相电压基波峰值为:

(10)

通过调节调制因子m可以实现交流侧输出电压的升高与降低,由此扩大了准Z源逆变器的使用范围,使其应用更加广泛.

1.3 并网系统的数学建模

光伏并网系统模型如图3所示.其状态空间方程所列如下:

图3 并网光伏系统模型

(11)

转换为同步旋转d-q坐标系下的方程为

(12)

式中:ua,ub,uc——电网电压;

ia,ib,ic——逆变器并网电流;

L——每相电路的滤波电感;

R——传输导线和电感上的相电阻;

Ti——逆变器上下桥臂IGBT的通断情况,i=1,2,3;

id,iq——d-q坐标系下的交流电流;

ud,uq——d-q坐标系下的交流电压;

Dd,Dq——d-q坐标下电力电子开关管的占空比.

当Ti=0时,上桥臂IGBT导通,下桥臂IGBT截止;当Ti=1时,下桥臂IGBT导通,上桥臂IGBT截止.

2 滑模变结构控制器的设计

2.1 准Z源逆变器光伏输出电压滑模变结构控制

假设准Z源阻抗网络的电感、电容足够大且系统的开关频率也足够大,忽略准Z源网络电感的内阻[5],则在稳态时,一个开关周期内电感L1的电流为恒定值,即:

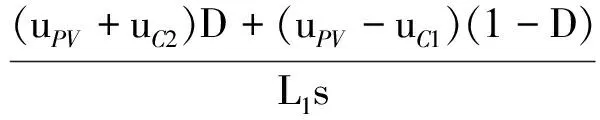
(13)

由电容特性可得光伏输出电压闭环传递函数为:

uPV(s)=

(14)

将式(14)变换到时域后再求导,得:

(15)

2.1.1 寻找滑模面s

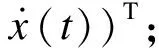
则有:

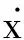
(16)

设计滑模面为:

(17)

所设计的滑模面适用于典型的反馈控制,其中若C>0,求解微分方程时,明显e(t)会趋于零.故满足选择的滑模面的要求.

2.1.2 选取控制器u(t)

对式(17)求导得到:

-f(X)-bu(t)-D(X,t))

(18)

式中:xd——光伏输出电压瞬时值.

采用指数趋近律:

(19)

式中,ε,k>0.

当s较大时,系统状态会以较大的速度趋近于滑模面;当s接近于零时,趋近速度不是零,从而保证了在有效时间内达到最大功率点跟踪.

故取控制率u(t)为:

(20)

由于D(X,t)具有不确定性,故需要有一个固定的DC,它与D(X,t)的边界有关,即:

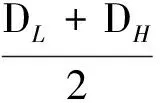
(21)

得到新的滑模变结构控制率为:

(22)

因此有:

(23)

2.1.3 验证

2.2 准Z源逆变器并网系统滑模变结构控制

由式(4)可以推导id的参考值为:

(24)

式中:Pref——光伏阵列输出的最大功率,由MPPT控制器按照一般的扰动观察法给出.

根据电压定向控制原理,假设开始(t=0)时d轴与a轴重合,只要逆变器并网的三相电流满足式(4),就能达到上述控制目标,即:iq=0,id=iref.因此,逆变器并网电流的参考值iaref,ibref,icref选取为:

(25)

2.2.1 寻找滑模面

假设滑模面函数为:

(26)

2.2.2 选择控制率

由式(26)可得:

(27)

式中:ua-con,ub-con,uc-con——逆变器的三相端电压.

选取控制率为:

(28)

2.2.3 验证

(1) 能达性 当ka,kb,kc满足

(29)

3 仿真研究

为了验证上述理论分析结果的正确性,对系统进行了仿真验证.系统仿真模型的简化图如图4所示.

图4 系统仿真模型

其主要的参数如下:准Z源网络的电容C1=C2=1 000 μF,电感L1=L2=400 μH,开关频率TS=10 kHz,滤波电容CPV=1 000 μF.光伏电池参数如下:参考温度为25 ℃,参考光照强度为1 000 W/m2下的开路电压UOC=45.5 V,短路电流ISC=5.6 A,额定功率Pm=190 W.最大功率点跟踪采用扰动观察法[6].

假设环境温度为25 ℃,保持不变,在1.5 s时光照强度从1 000 W/m2突变为500 W/m2,分别对有滑模变结构控制与无滑模变结构控制进行仿真.无滑模变结构的控制就是在图4的基础上,去掉两个滑模控制器进行仿真.

有/无滑模变结构控制下的光伏发电系统部分的upv和ipv波形如图5和图6所示.对比图5和图6可以看出,有滑模变结构控制的光伏发电系统输出的upv和ipv波形更加平滑,抖动、谐波更少.

有/无滑模变结构控制下的光伏逆变并网侧的电压ua,ub,uc在时间域为0～2 s,1.4～1.6 s的波形如图7和图8所示.对比图7和图8可以看出,有滑模变结构控制的伏逆变并网侧的电压ua,ub,uc波形更加平滑一点,出现的抖动更少.

由此可见,滑模变结构控制能够增强系统的鲁棒性,在光照发生突变的情况下,在光伏发电部分加入滑模变结构控制能够更加快速跟踪光伏输出的电压与电流,系统的鲁棒性有所提高;在光伏并网逆变器控制部分加入滑模变结构控制能够有效地提高系统鲁棒性,同时也提高了并网的电能质量.

图6 光伏发电系统输出电流

图7 时间域为0～2 s的光伏逆变并网侧的ua,ub,uc波形

图8 时间域为1.4～1.6 s的光伏逆变并网侧的ua,ub,uc波形

4 结 语

本文提出了一种双滑模变结构控制的新方法:在光伏发电系统和并网系统中分别加入滑模变结构控制.通过有滑模变结构控制与无滑模变结构控制的实验仿真比较可知:在光伏发电部分加入滑模变结构控制,能够更加快速跟踪光伏输出的电压与电流,系统的鲁棒性有所提高;在光伏并网逆变器控制部分加入滑模变结构控制,能够有效地提高系统鲁棒性和并网的电能质量.其不足之处在于:系统的响应速度没有明显提高;仿真波形虽然有所改进,但谐波依然存在.

[1] 李军红,洪镇南.三相光伏并网系统的滑模变结构控制[J].电力系统保护与控制,2012,40(12):83-87.

[2] 何翔,张代润.基于滑模控制的三相光伏并网逆变器研究[J].电源技术,2014,38(4):672-675.

[3] 刘胜杰,吴苓芝.一种准Z-源DC-DC变流器的研究[J].微型机与应用,2012,31(17):33-36.

[4] 郭会娜,黄洪全.扰动观察法与滞环比较法实现MPPT的比较分析[J].太阳能,2008,11(11):30-32.

[5] BANAEI M R,DEHGHANZADEH A R,SALARY E,etal.Z source-based multilevel inverter with reduction of switches[J].IET Power Electronics,2012,5(3):385-392.

[6] 陈宗祥,蒋赢,潘俊民,等.基于滑模变结构控制的Z源逆变器在单相光伏系统中的应用[J].中国电机工程学报,2008,28(21):33-39.

DoubleSlidingModeControlofPhotovoltaicSystemBasedonQuasiZSourceInverter

XUE Yang, ZHENG Rong, KAN Dongyue, SHI Yufei, ZHENG Mengqiu

(SchoolofAutomationEngineering,ShanghaiUniversityofElectricPower,Shanghai200090,China)

As a new type of circuit topology structure,quasi Z source inverter can reduce the voltage and current ratings of inverter,and enable the input current of inverter to be more continuous in addition to the advantages of Z source inverter.The benefits of double sliding mode control are analyzed.In the part of generating photovoltaic system,the sliding mode control can track the output voltage more rapidly,achieving the aim of maximum power point tracking.In the part of grid-connected system,sliding mode control can effectively improve the response of system and the quality of power.By simulation,the accuracy of the model and effectiveness of the control system are obtained.

quasi Z source inverter; sliding mode control; maximum power point tracking; photovoltaic power generation

10.3969/j.issn.1006-4729.2017.05.010

2016-12-28

郑蓉(1993-),女,在读硕士,江苏淮安人.主要研究方向为光伏发电.E-mail:15996553382@163.com.

上海市自然科学基金(13ZR1417800);国家自然科学基金(51405286);上海市重点科技攻关计划项目(14110500700);上海市电站自动化技术重点实验室项目(13DZ2273800).

TM615;TM464

A

1006-4729(2017)05-0459-07

(编辑 胡小萍)