钢波纹管的力学性能分析
尤 佺 缪林昌 董冬冬
(1东南大学岩土工程研究所, 南京 210096)(2上海市政工程设计研究总院(集团)有限公司, 上海 200092)
钢波纹管的力学性能分析
尤 佺1缪林昌1董冬冬2
(1东南大学岩土工程研究所, 南京 210096)(2上海市政工程设计研究总院(集团)有限公司, 上海 200092)
提出采用截面参数分析法与有限元数值模拟相结合的方法对钢波纹管受力变形进行计算分析.将截面参数分析法所得计算结果与美国ASTM规范对比,验证了截面参数分析法的有效性.根据截面参数计算结果将钢波纹管道等效为实壁管道,并在此基础上对应不同工况建立有限元数值模型,进一步研究了钢波纹管道在填土施工过程中的变形与内力特性,总结了其力学性能与填土高度、管道规格的对应关系和钢波纹管道设计中的建议管道规格.最终根据钢波纹管道施工现场工况,对管周土体竖向土压力及管道环向应变进行计算,通过与现场实测数据对比,验证了该方法模拟钢波纹管管土相互作用的有效性.研究表明所提出的钢波纹管分析方法简便准确,并能很好地再现钢波纹管道的力学特性.
钢波纹管道;等效方法;力学性能;现场施工
钢波纹管因施工快捷、经济的特点逐渐被工程界接受,一些科研人员也开始针对钢波纹管的力学性能进行研究.蒋雪梅等[1]采用ANSYS通用程序中的Shell93单元沿波长方向对管道波纹直接进行等分以模拟波纹并建立数值模型进行分析;韩晓强[2]将半波长波纹管划分为五节点,波纹管模型划分为三角形的小网格研究了钢波纹管道的受力情况;王艳丽等[3]采用薄壳理论对钢波纹管道进行等效分析;粟缤[4]在此基础上,将波纹形状设为给定波形绕轴线旋转一周形成的旋转面,通过Midas建立数值模型分析波纹管道的受力状况.国内对波纹管的研究主要以数值计算分析为主.美国、加拿大等国已制定了相应的规范[5-7],在实际使用中以小直径钢波纹管居多.近年来,钢波纹管道开始向高填土大跨径发展.
本文在提出并验证截面参数分析法的基础上,利用PLAXIS软件建模,分析钢波纹管的力学性能,并研究不同规格钢波纹管道力学特性与填土高度之间的关系;基于数值模拟结果提出了适用于不同工况的最佳管道规格参数及设计要点;最后将钢波纹管道施工现场实测数据与数值计算结果进行对比,以验证本文提出的钢波纹管道分析方法的有效性.
1 模型建立与验证
1.1 波纹管道截面参数的确定及验证
波纹管道的截面参数是波纹管道研究中的重要参数,与波距×波高、壁厚、管径等参数相比,波纹管的截面参数惯性矩更为关键.
以美国ASTM规范[8]中152 mm×51 mm(波距×波高)规格的钢波纹管为例,阐述计算波纹管道截面参数的方法.ASTM规范中152 mm×51 mm规格钢波纹管波纹的尺寸如图1(a)所示.
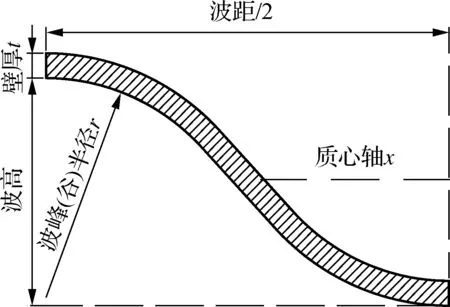
首先根据波距、波高、波峰(谷)半径以及壁厚4个参数,建立一个波纹长度的纵截面图形,半个波纹长度的截面如图1(b)所示.
图1(c)为1个波纹长度的纵截面面域单元.求出1个波纹长度对应的x轴截面惯性矩及面积并除以1个波距,即可得到管道总截面每延米管壁的惯性矩I和面积A等截面参数.
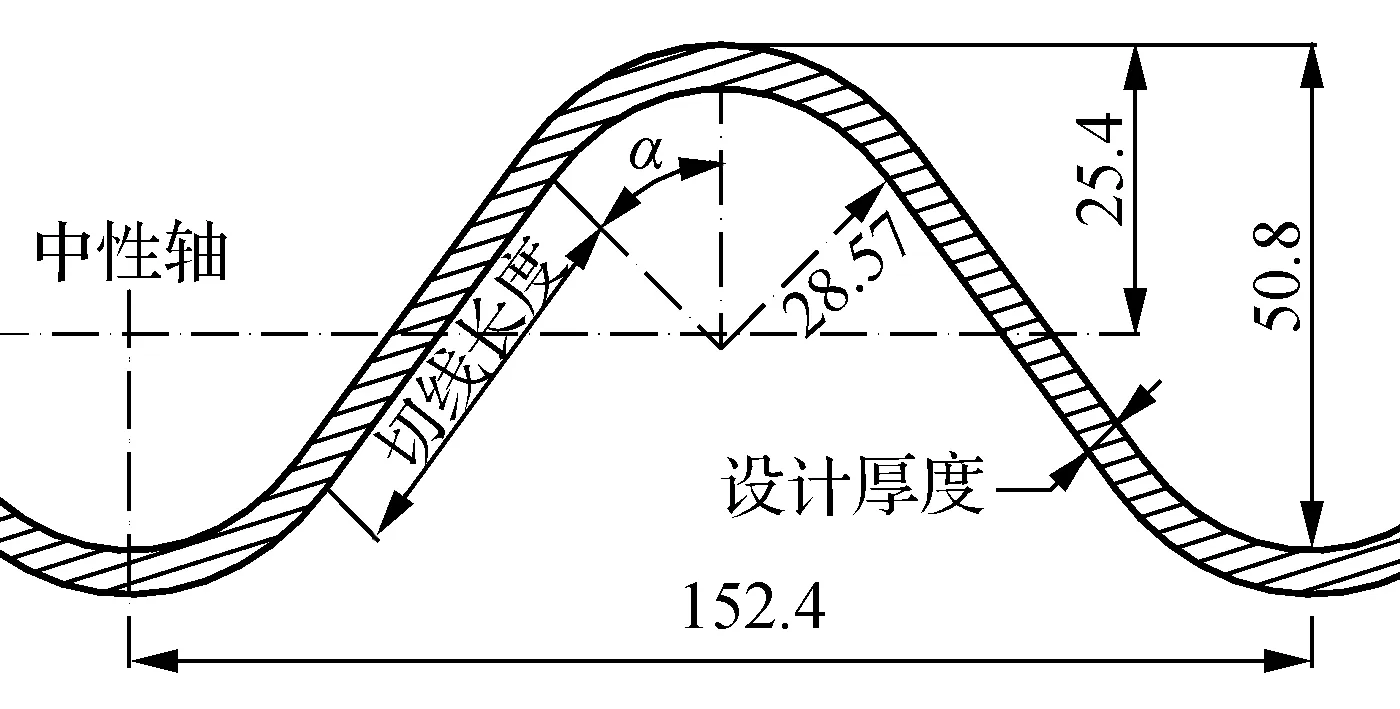
(b) 波纹纵截面示意图
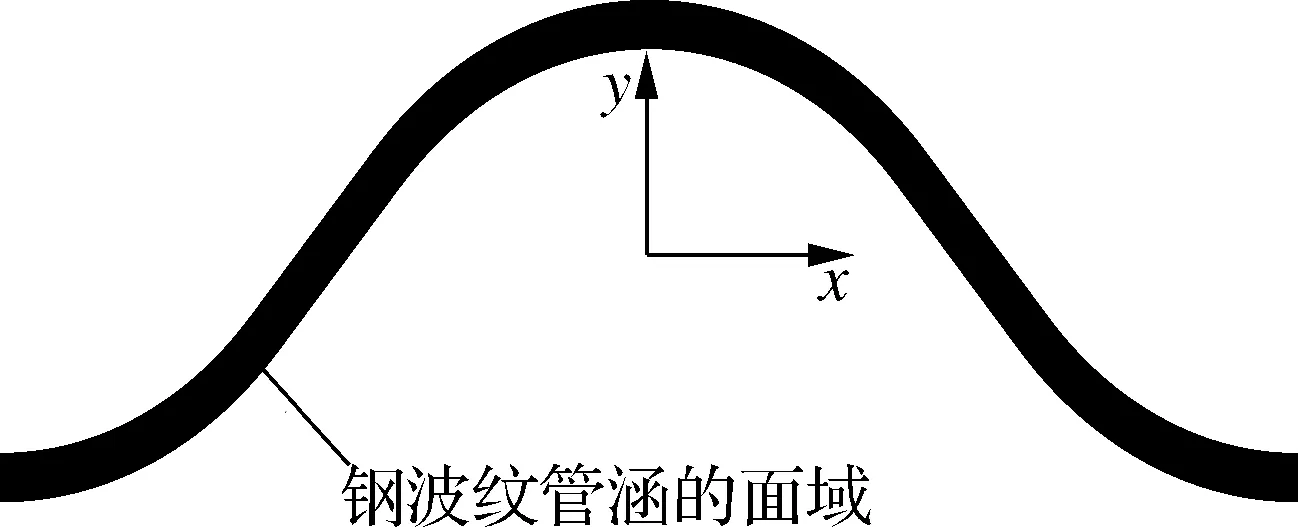
(c) 波纹管纵截面面域
对不同设计厚度的波纹管道进行截面参数计算,结果如表1所示,并与ASTM规范中规定的波纹钢板截面参数进行对比.
由表1可知,计算得到的截面参数与美国ASTM规范提供的数据非常接近(误差小于1.5%),表明波纹管的截面计算法可行.并且,由于各规范使用波形不同且缺乏相应的物理力学参数,波纹管截面计算法使计算效率大幅提高.

表1 截面计算法分析结果与美国ASTM规范对比
1.2 钢波纹管道有限元模型的建立
在钢波纹管道截面参数计算的基础上,将波纹管道等效为相同内径实壁管道,再采用有限元分析软件PLAXIS进行分析.
依据《公路桥涵施工技术规范》[9],针对平原地区及山地地区的常见工况分别建立数值模型,具体设计工况见表2.由表可发现,M类(山地地区)工况与P类(平原地区)工况最主要的区别是填土高度不同,M类工况填土高度相对较高,因此土拱效应发挥的作用更显著.
为研究钢波纹管道力学特性与填土高度之间的关系,分别对P,M两类工况的不同工程特性,设
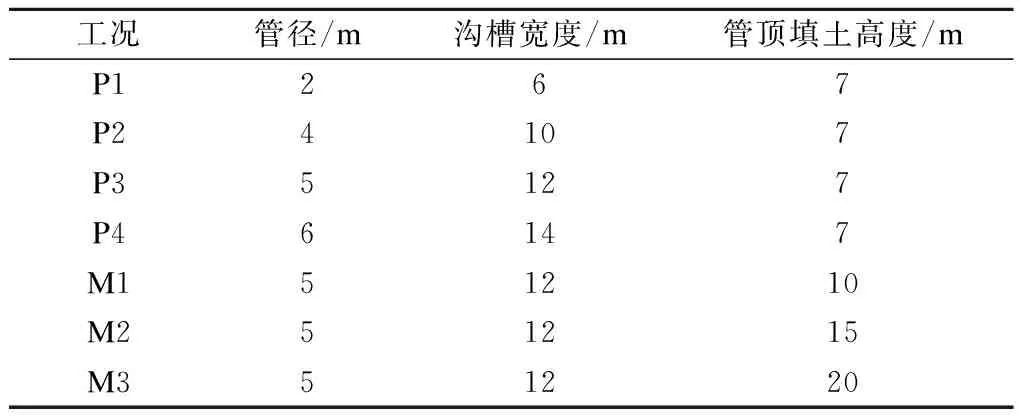
表2 数值模拟工况
计不同的管道规格,以分析其在填土施工过程中的力学特性.P类工况中采用壁厚为2,3,4,5,6 mm,波距×波高为68 mm×13 mm, 125 mm×25 mm, 150 mm×50 mm, 200 mm×55 mm的波纹管道;M类工况采用的波纹管道规格为壁厚4,5,6,7 mm,波距×波高为150 mm×50 mm,200 mm×55 mm,400×150 mm.
为简便表达波纹的形状,将壁厚规格2,3,4,5,6,7 mm分别设为A,B,C,D,E,F,而波距×波高的规格68 mm×13 mm,125 mm×25 mm,150 mm×50 mm,200 mm×55 mm,400×150 mm设为a,b,c,d,e.以壁厚为2 mm、波距×波高为68 mm×13 mm的波纹管为例,其波纹形状表示为Aa.
Corey等[10]提出,模型计算范围应为管道尺寸的5倍及以上,可避免边界效应对管道的影响.参考规范[9,11-12],P类工况设计模型尺寸为50 m×35 m,而M类工况由于管顶填土高度不同分别设计尺寸为50 m×35 m, 50 m×40 m和50 m×45 m.数值模型的尺寸和土体分层情况如图2所示(以工况P3为例).对回填土体采用摩尔-库伦准则进行模拟,钢波纹管道使用板单元进行模拟.模型的左右边界施加水平约束,模型的下边界施加竖向和水平约束.
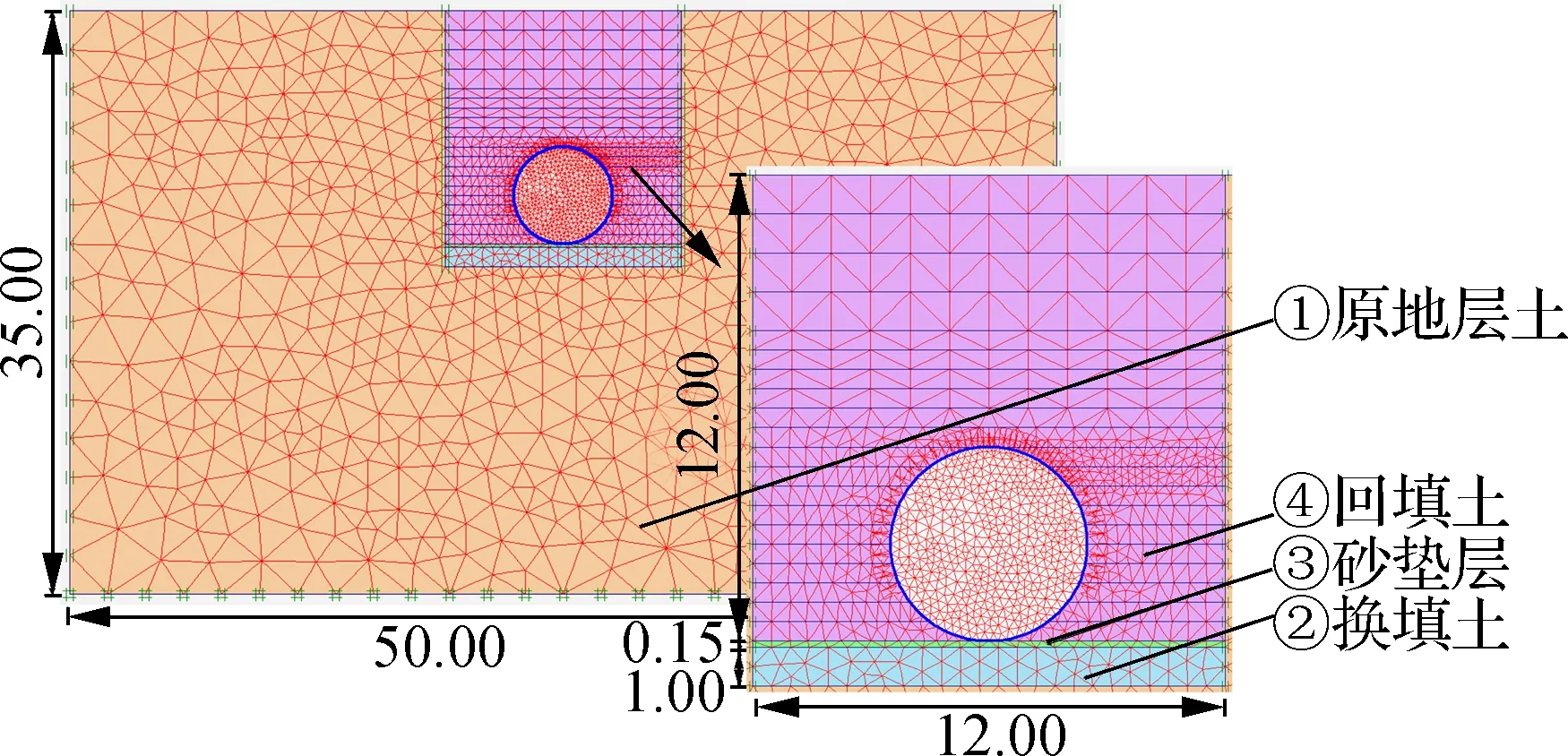
图2 工况P3有限元数值模拟模型(单位:m)
建模步骤如下:① 确定不同位置处土体的压实度及相关参数,见表3;设置管土作用界面单元Rinter参数值为0.7.② 模拟管道施工填土过程逐层填土(管底至管顶3 m填土高度每层0.4 m,管顶3 m至地表每层0.8 m).③ 对管道及管周土体进行压实模拟.为简化计算,本文不考虑地下水的影响.
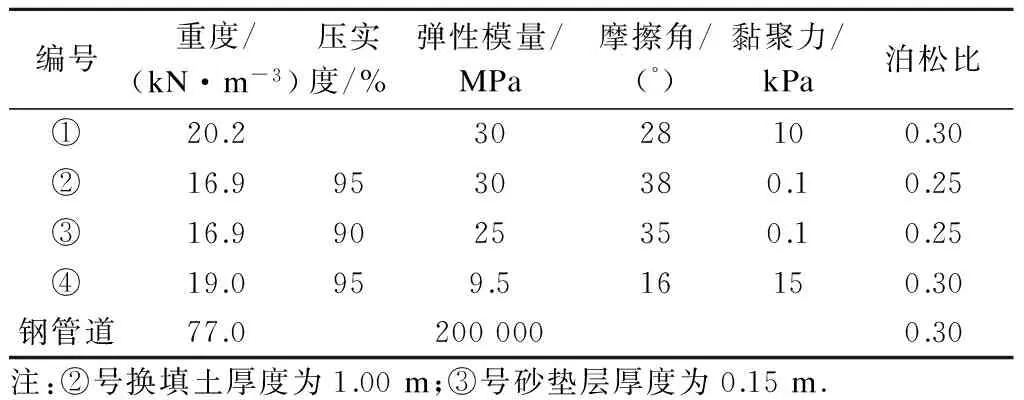
表3 数值模型中的材料参数
2 钢波纹管道的变形分析
2.1 填土过程中管道的变形
管道施工回填过程中竖向和水平向变形随管顶填土高度的变化如图3所示(以工况P1为例),管道变形为正值表明管道在该方向处于拉伸状态,反之则处于压缩状态.由图3可发现,管道水平向变形一直为正值(拉伸),而竖向变形一直为负值(压缩),这说明从放管至填土结束,管道一直处于类似横向椭圆的形态.
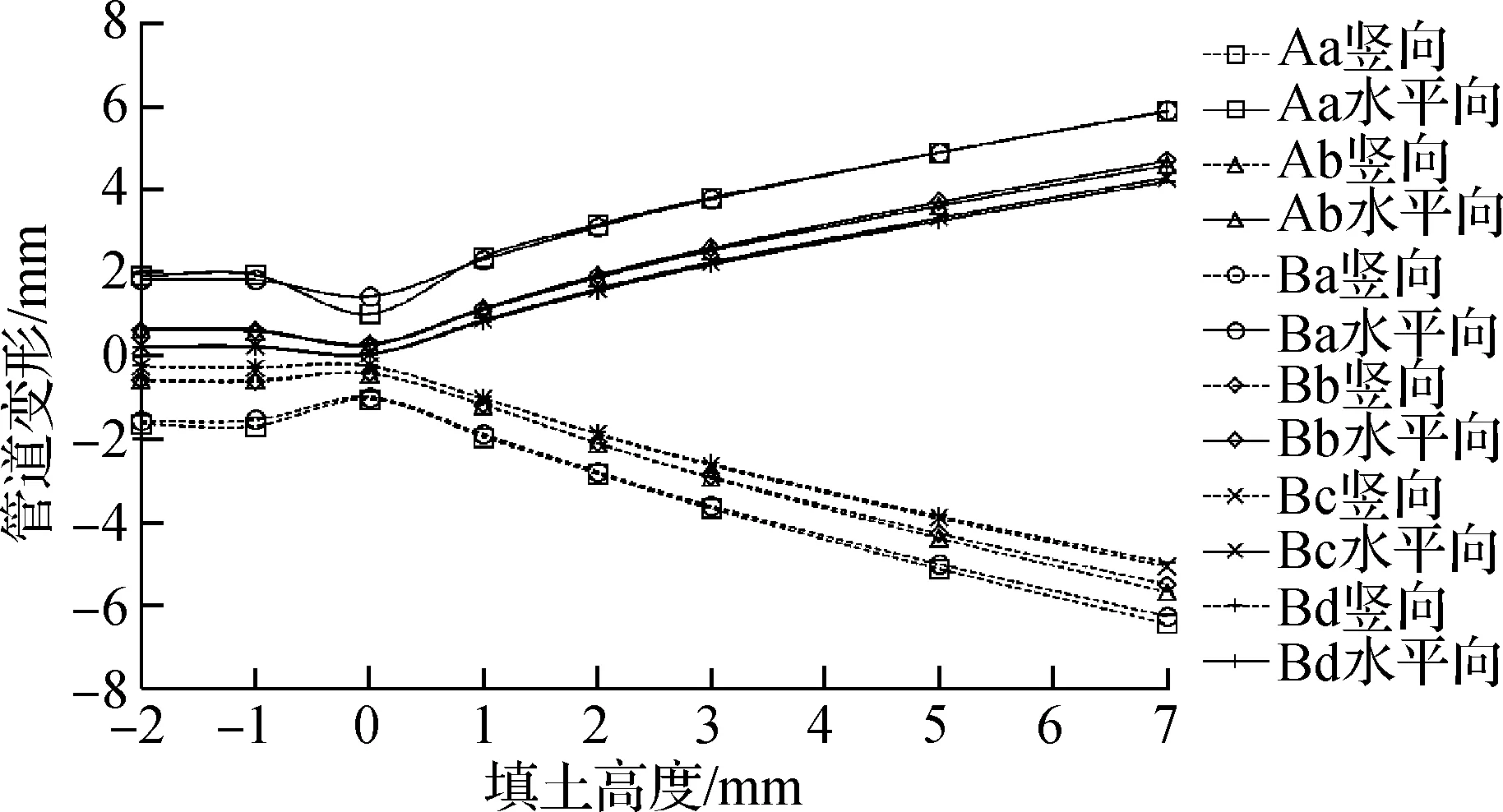
图3 填土过程中管道变形随填土高度的变化(工况P1)
由图3分析可得管道变形与填土高度的对应关系如下:
① 放管后填土前,管道在自重作用下即出现了相应的竖向和水平向变形.因此在放管时,尤其对于较大直径的管道有必要做好管道的临时支撑.
② 填土从管侧至管顶的过程中,管道受两侧土压力的作用,管道水平向与竖向变形均减小,这与Sargand等[13]给出的“峰值特点”相类似;填土超过管顶所在的水平面后,竖向变形与水平向变形逐渐增大,这主要是由于填土高度增大后土的竖向压力加大造成的.
③ 整个填土过程中,竖向变形与水平变形的绝对值随填土高度的变化规律保持一致,但竖向变形值略高于水平变形.
2.2 填土过程中波距×波高和壁厚与管道变形的关系
为便于分析,引入管道挠度的概念.管道管顶挠度与管侧挠度定义为
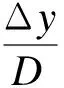
(1)
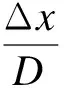
(2)
式中,D为管道直径,mm;Δy为竖向变形,mm;dy为管顶挠度,%;Δx为水平向变形,mm;dx为管侧挠度,%.管顶及管侧挠度统称为管道挠度.
管顶挠度对应着管道施工中最大的挠度,因此取管顶挠度为研究对象.管道施工回填完成后管顶挠度与波距×波高、壁厚的关系如图4所示(以工况P1和P2为例).
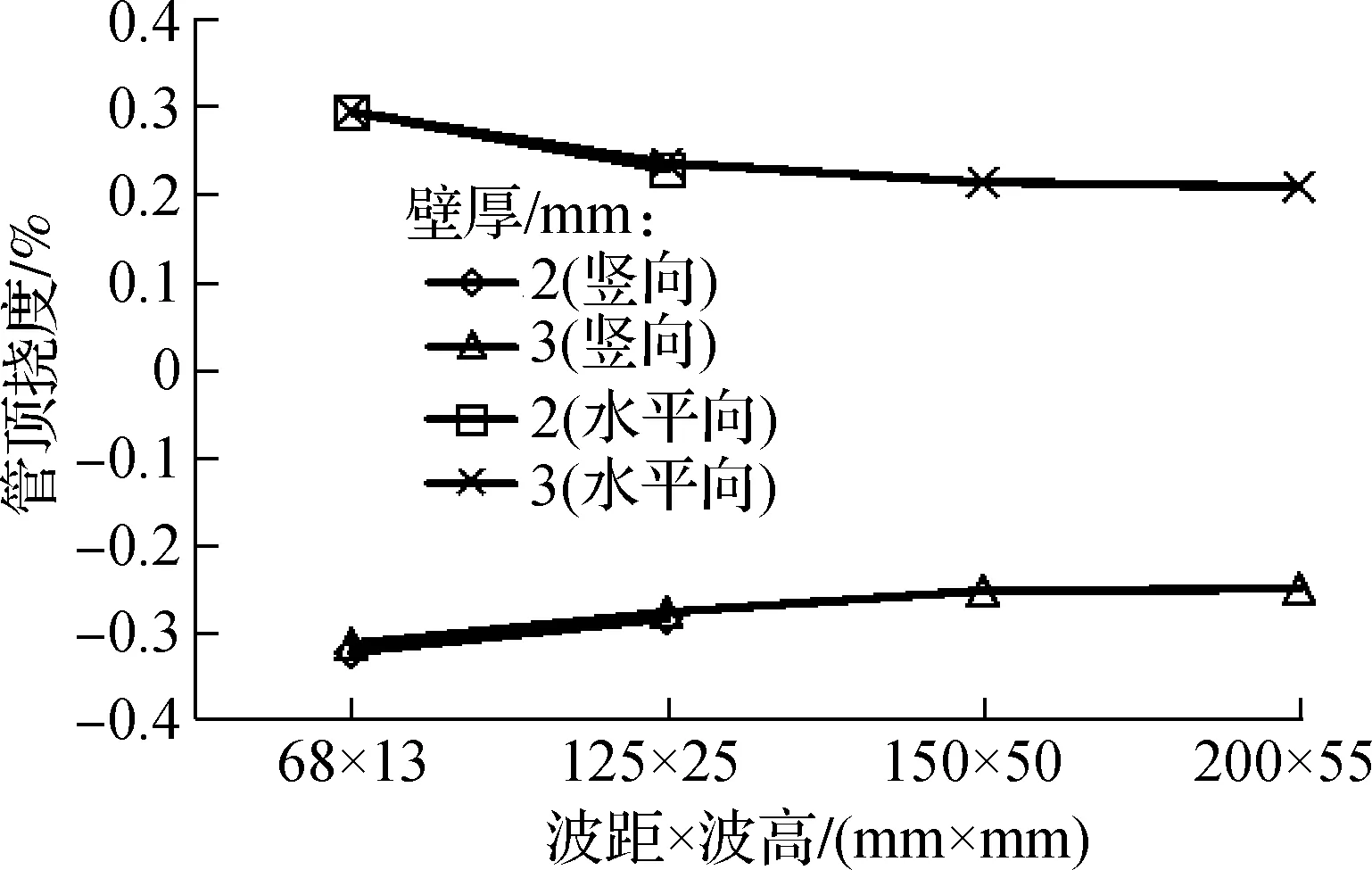
(a) 工况P1
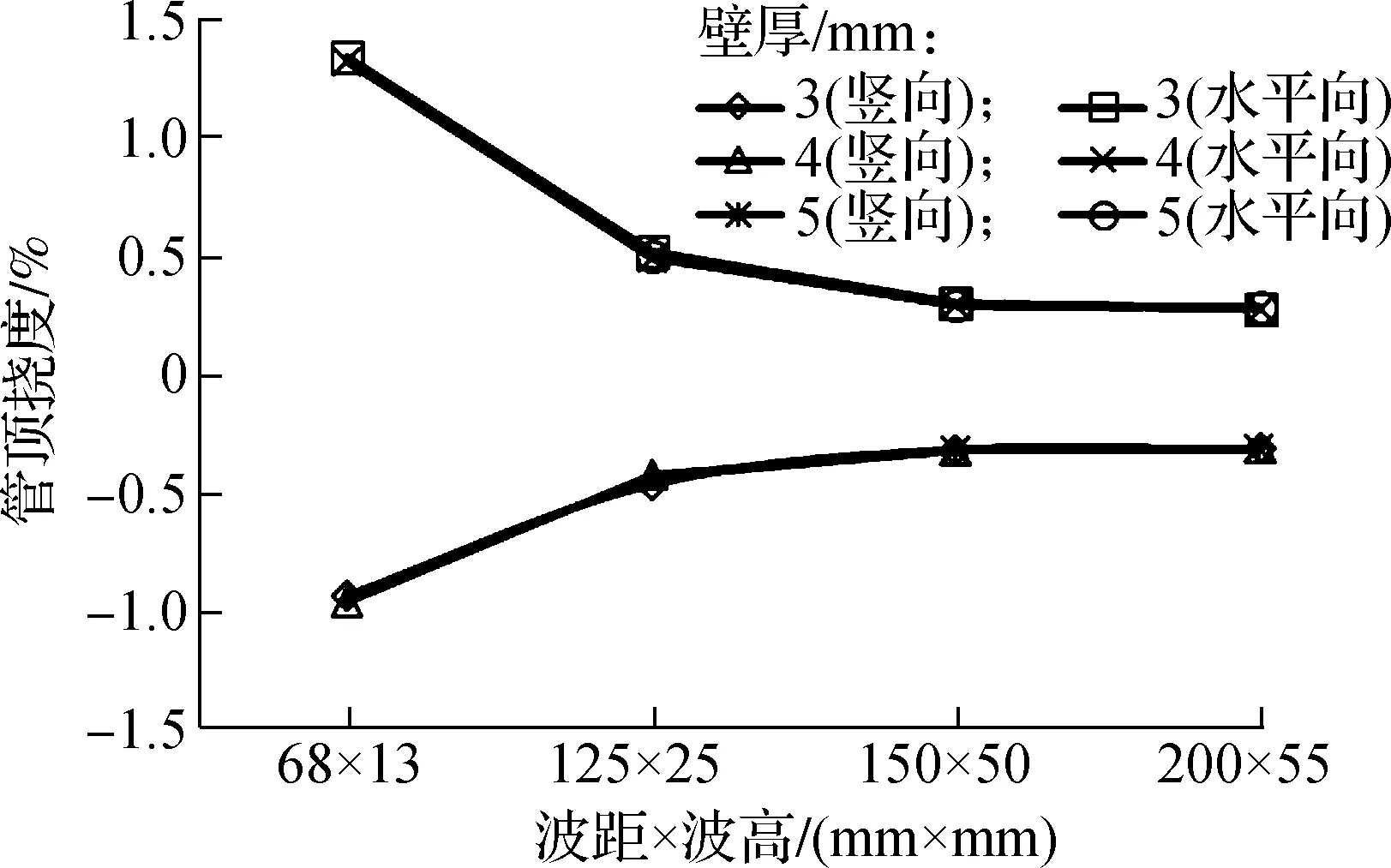
(b) 工况P2
由图4可得:
① 相同波距×波高条件下,填土高度相同时,不同壁厚的管道变形几乎一致,故在满足强度要求的前提下,壁厚的增加对变形影响不大.
② 随着管径的增大,小壁厚的管道在填土过程中会发生破坏.比较图4(a)与图4(b),工况P2中管径为4 m时不能使用壁厚为2 mm的波纹钢管,否则将发生破坏;因此需设置一定的壁厚以满足强度要求.
③ P类工况中,波距×波高对变形影响较大;随着波距×波高的增大,竖向和水平向变形首先不断减小,然后会趋于稳定.
2.3 钢波纹管道参数的选取
施工过程中钢波纹管道的力学性能对于安全设计与施工具有重要意义.Carrier[14]指出应通过控制挠度或者弹性内力屈服以指导柔性管道的设计;特别在回填质量比较高的情况下,内力屈服很少受人关注,挠度控制是管道设计的主要手段.由2.2节分析可知,在壁厚满足强度要求的情况下,波距×波高增加至一定值后,管道挠度趋于稳定.因此,需在控制管道挠度的前提下,确定相对经济的管道规格.
Whidden[15]研究发现,钢管挠度保持在5%以内,即可保证局部变形对管道的正常使用不产生影响.本文研究得出P,M类工况下建议的钢波纹管道规格,如表4所示.
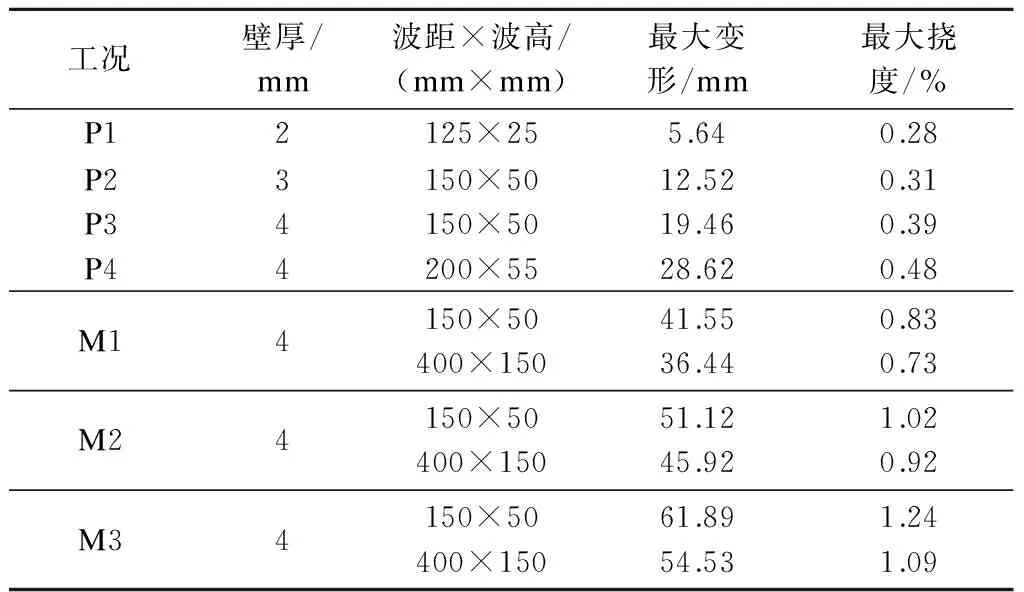
表4 不同工况下对应推荐钢波纹管道参数
由2.1节结论③可知竖向变形一直略大于水平变形,表中的最大变形即为此种工况的竖向变形; M类工况中波距×波高对填土完成后的管道变形影响不明显,因此变形控制较严格时,采用400 mm×150 mm规格的波距×波高,反之则采用150 mm×50 mm规格的波距×波高.
3 钢波纹管道内力分析
在钢波纹管道研究中发现,P,M类工况下管道的力学性能基本一致,在此仅对P类工况下的钢波纹管道的内力(轴力、剪力、弯矩)进行分析.内力符号的意义为:受拉为正值,受压为负值.
3.1 轴力
3.1.1 填土过程中管道轴力与填土高度的关系
填土过程中不同规格管道的最大轴力与填土高度的关系如图5所示(以工况P1为例).由图可见,对不同规格的管道,随填土高度的增大,管道轴力均不断增大;从管底至管顶填土时,轴力随填土高度呈加速增长,填土高度超过管顶后,轴力随填土高度均呈线性增长.
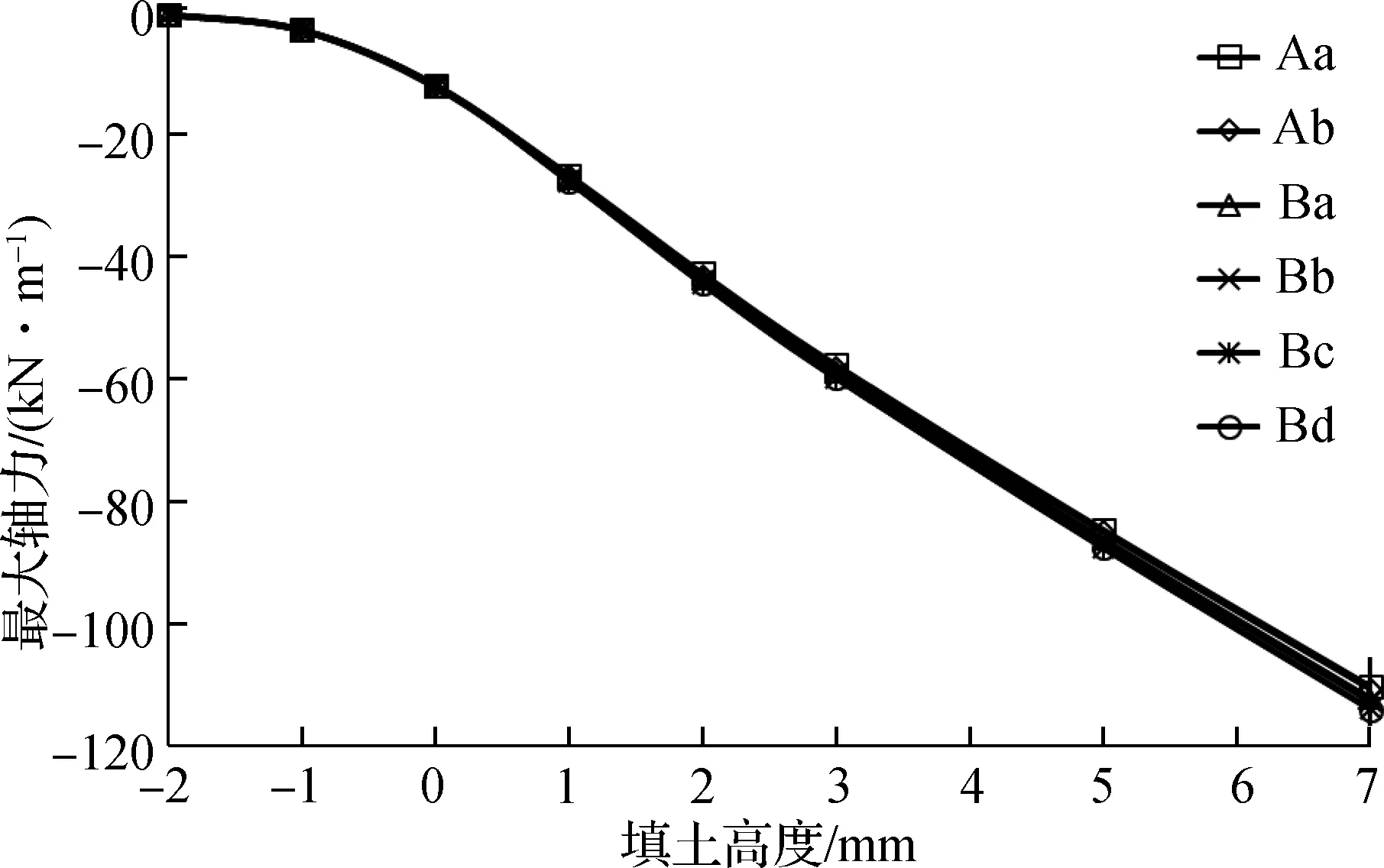
图5 填土过程中管道最大轴力与填土高度的关系(工况P1)
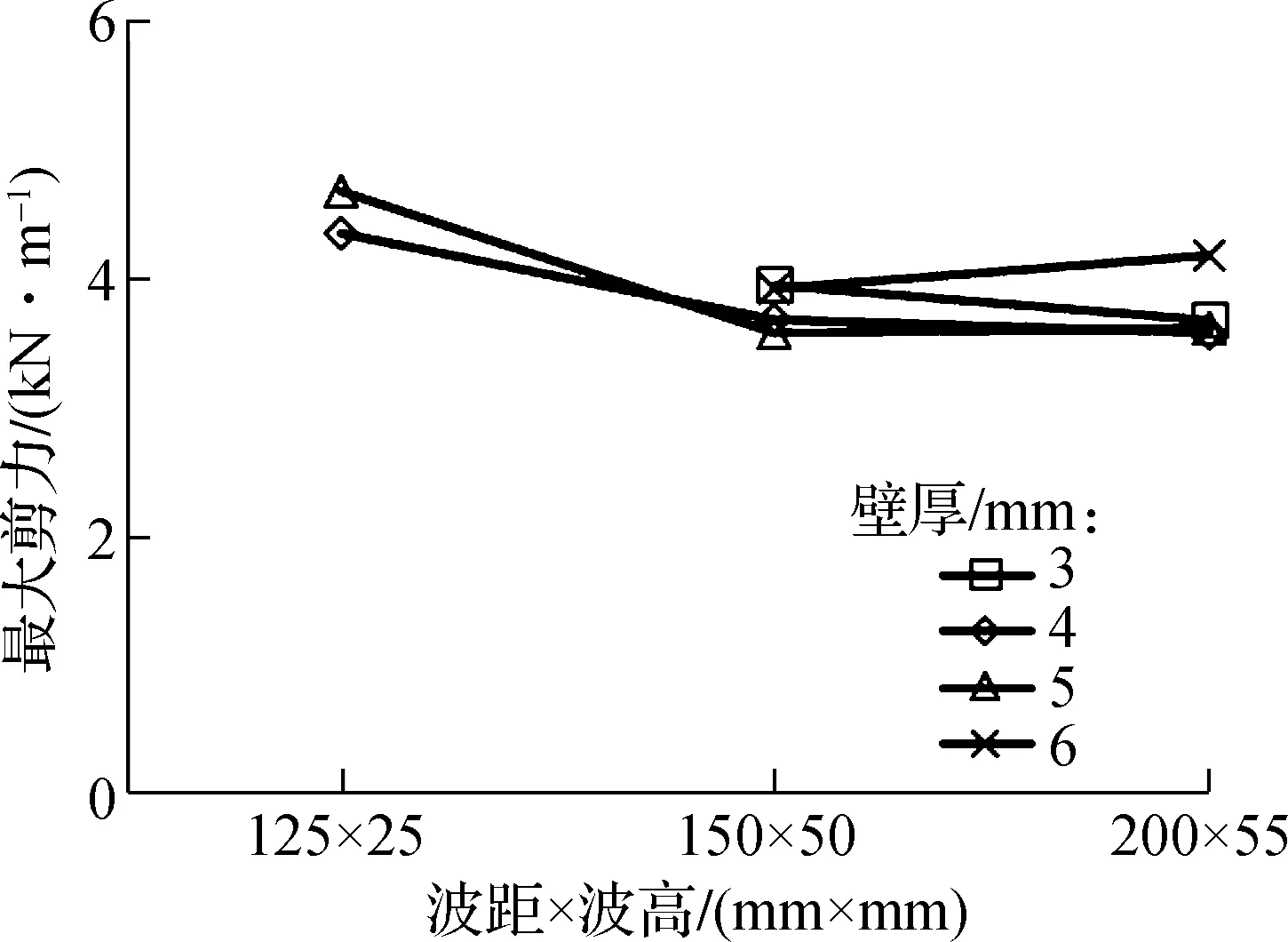
3.1.2 填土完成后波距×波高与管道轴力的关系
填土结束后,波距×波高对管道轴力的影响如图6(a)所示(以工况P2为例).由图可见,波距×波高增大时,轴力有略微增大;当波距×波高从150 mm×50 mm增大到200 mm×55 mm时,轴力已基本不变.结合2.2节中对变形的分析,波距×波高增加至150 mm×50 mm后,管道变形基本保持不变,因此轴力几乎不再增加.
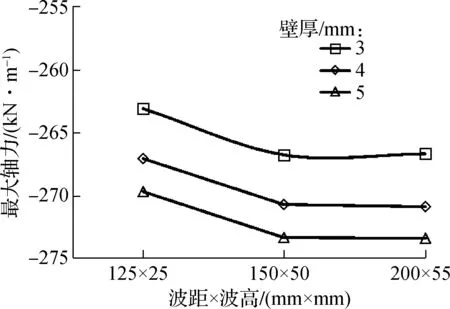
(a) 最大轴力与波距×波高的关系
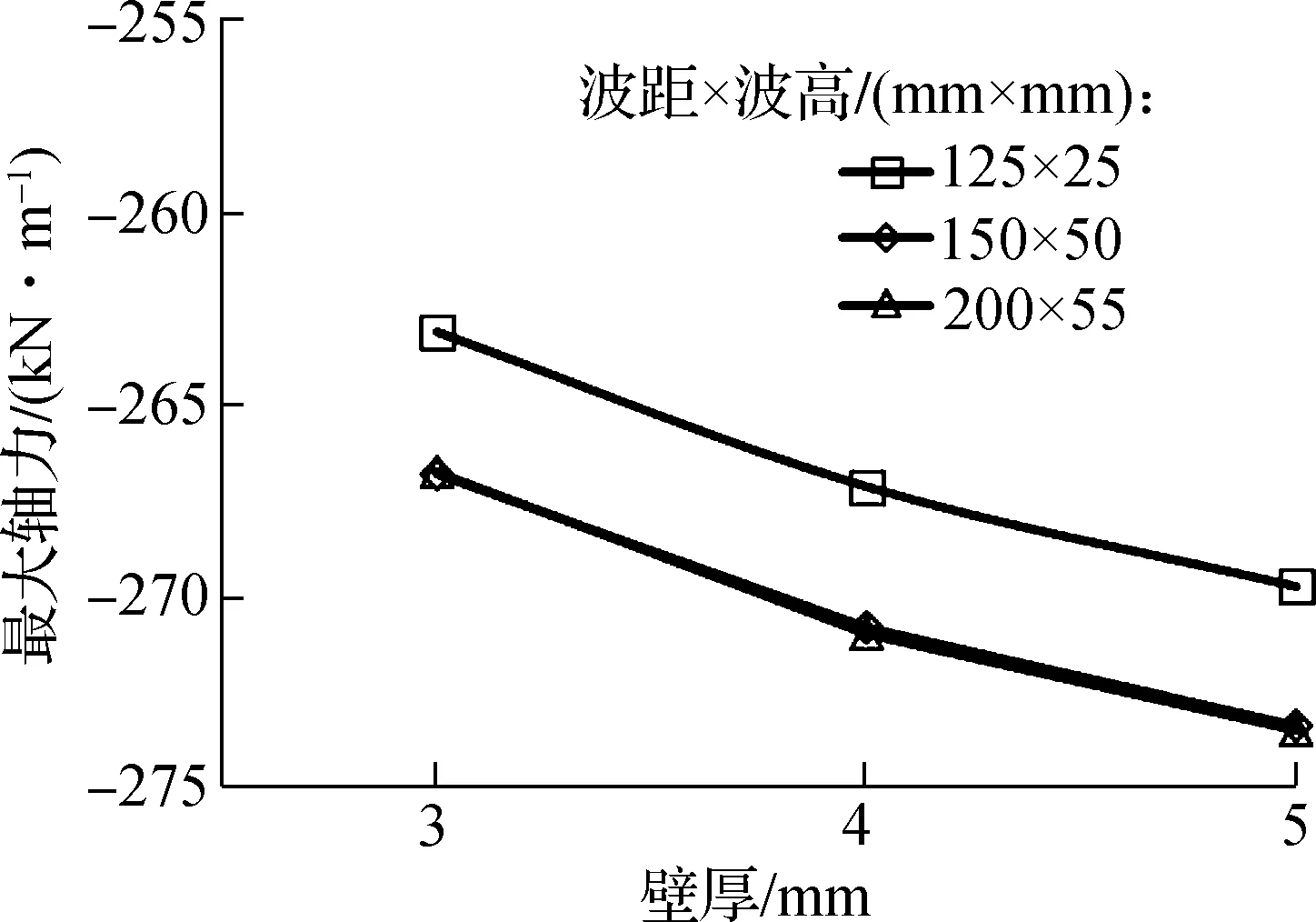
(b) 最大轴力与壁厚的关系
3.1.3 填土完成后壁厚与管道轴力的关系
管道填土结束后,壁厚对管道轴力的影响如图6(b)所示(以工况P2为例).由图可见,随着壁厚增大,轴力呈线性增长的趋势;但相比于初始壁厚对应的轴力初始量,增长幅度很小;这是由于在保证强度的前提下,壁厚对变形的影响很小所致.
3.2 剪力
3.2.1 填土过程中管道剪力与填土高度的关系
填土过程中管道的最大剪力与填土高度的关系如图7所示(以工况P1为例).由图可见,填土从管底到管顶的过程中,管道最大剪力有先减小后增大的趋势;填土至管顶后,管道与填土高度近似呈线性增长关系,线性关系较好.
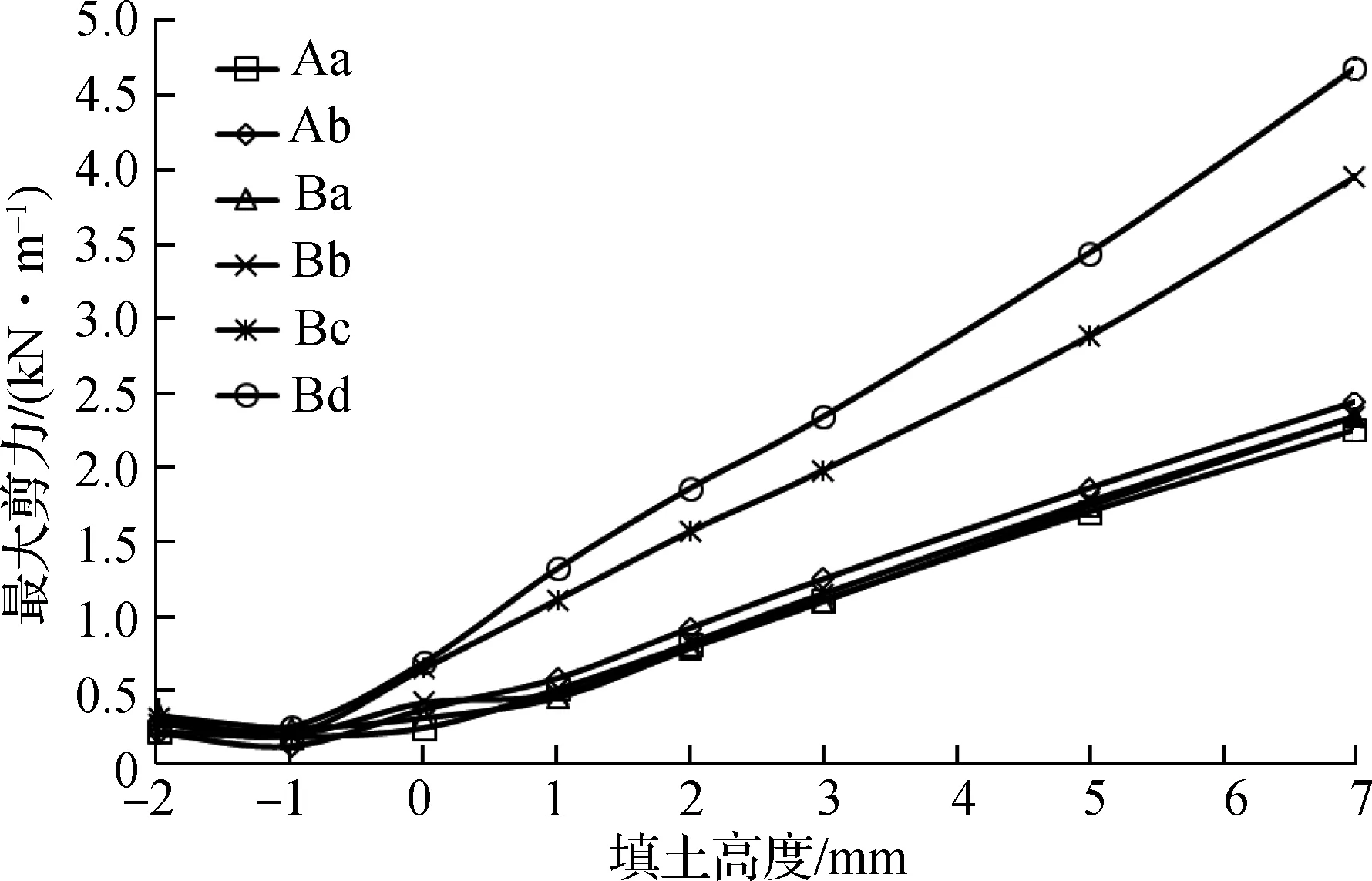
图7 填土过程中管道最大剪力与填土高度的关系(工况P1)
2.1节中对变形的研究表明,填土过程中管道会表现出“峰值特点”;由图7也可观察到,在填土至管侧附近时,伴随此现象波纹钢管各方向的差异变形最小,使得剪力也最小.
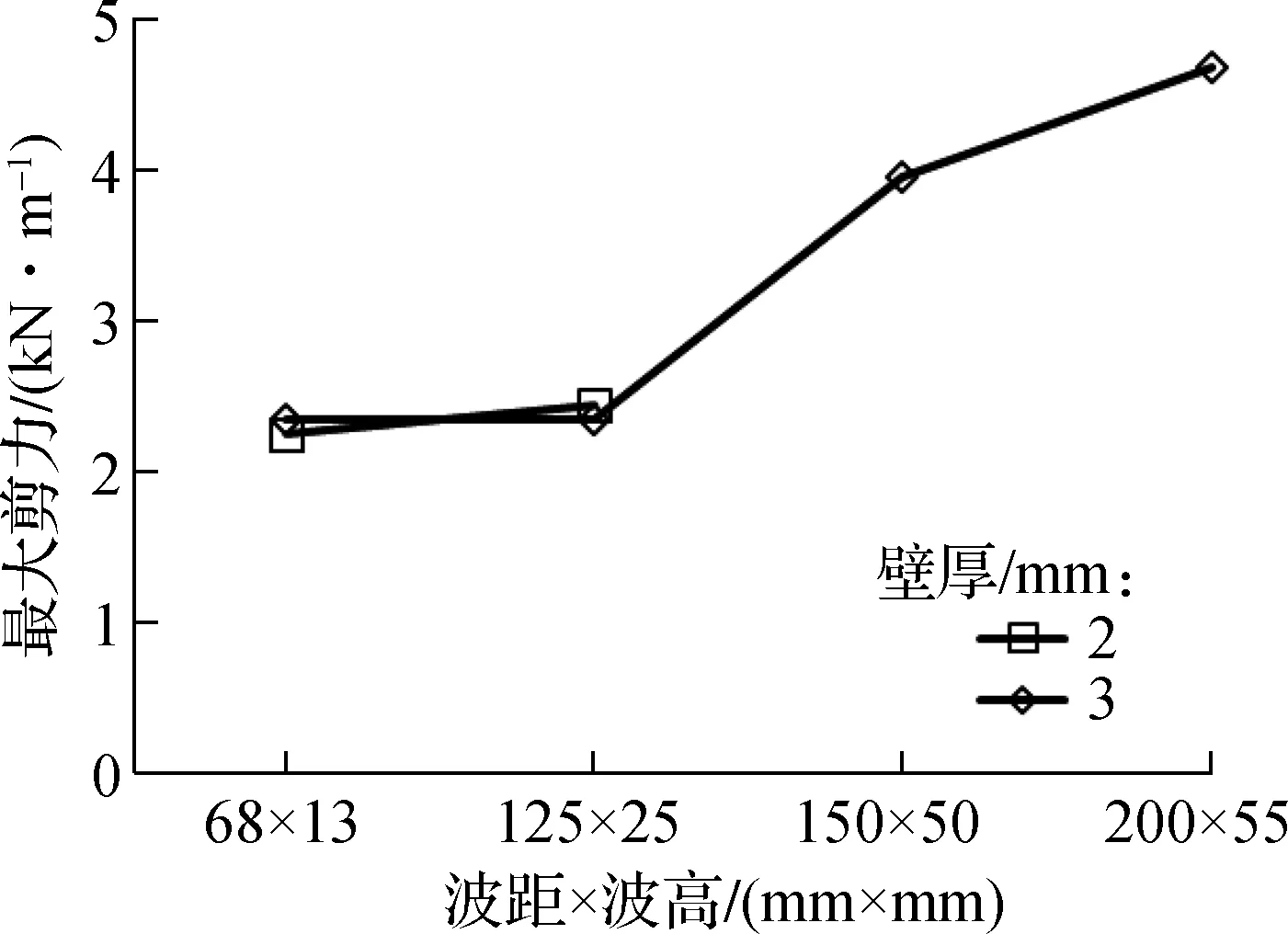
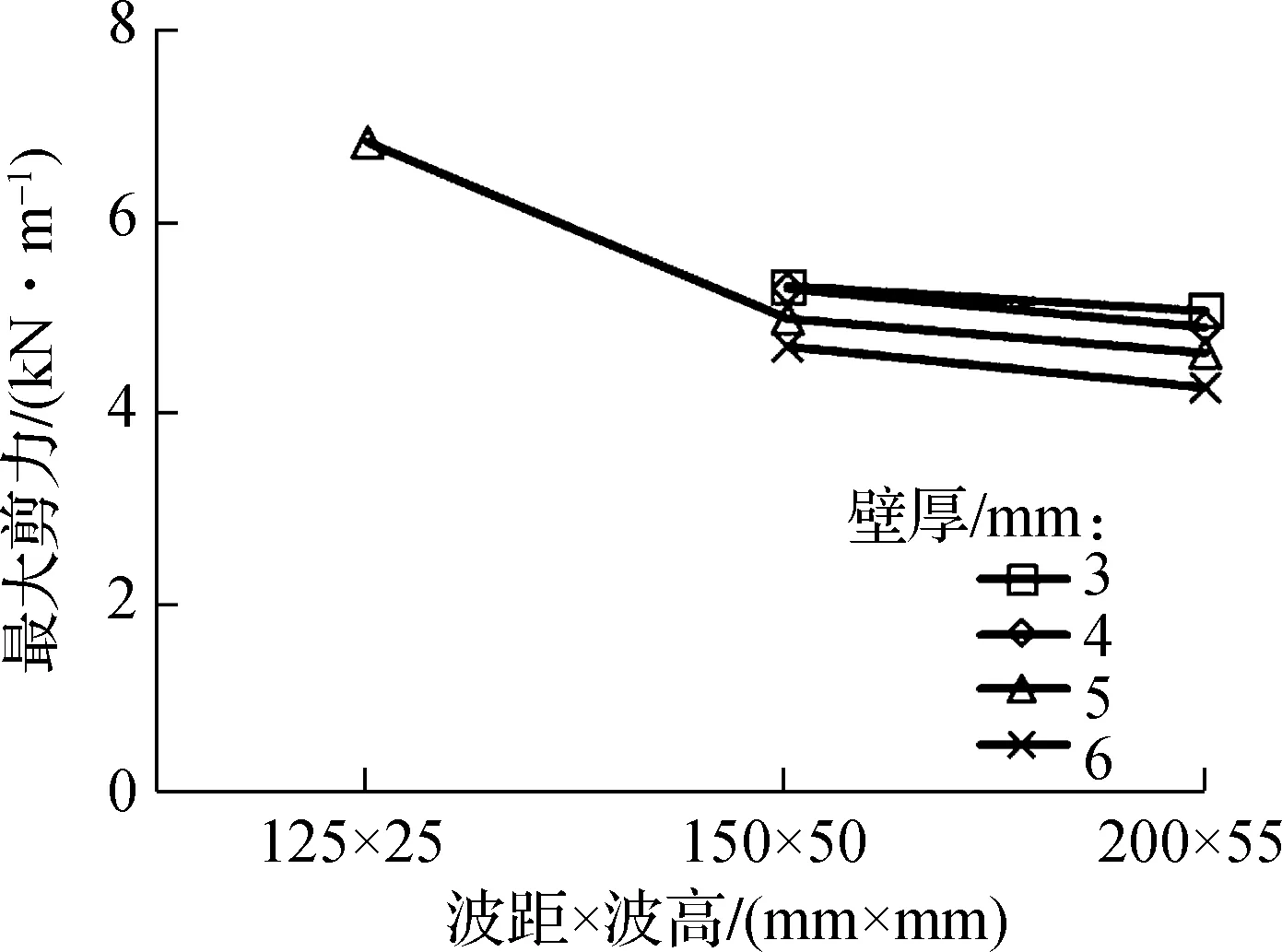
3.2.2 填土完成后波距×波高与管道剪力的关系
管道填土结束后,不同工况中波距×波高对管道剪力的影响如图8所示.由图可见,不同的工况对应不同直径的管道,当管径小于等于4 m时,随着波距×波高增大,剪力会增大,增大幅度逐渐减小;管径大于4 m时,随着波距×波高增大,剪力会减小,减小幅度逐渐减小.
对管径小于等于4 m的管道,波距×波高增加,变形减小,管土共同作用时可转移至土体中的压力减小,因此剪力增大;而对于管径大于4 m的管道,波纹钢管结构更接近于柔性,在土体荷载作用于管道前,管道已产生较大变形,上部荷载充分转移至管道周围的土体中,增加波距×波高对土拱效应影响不明显,此时由于管道自重变形引起的剪力变化占主导地位,因此波距×波高越大,管道变形越小,剪力也越小.
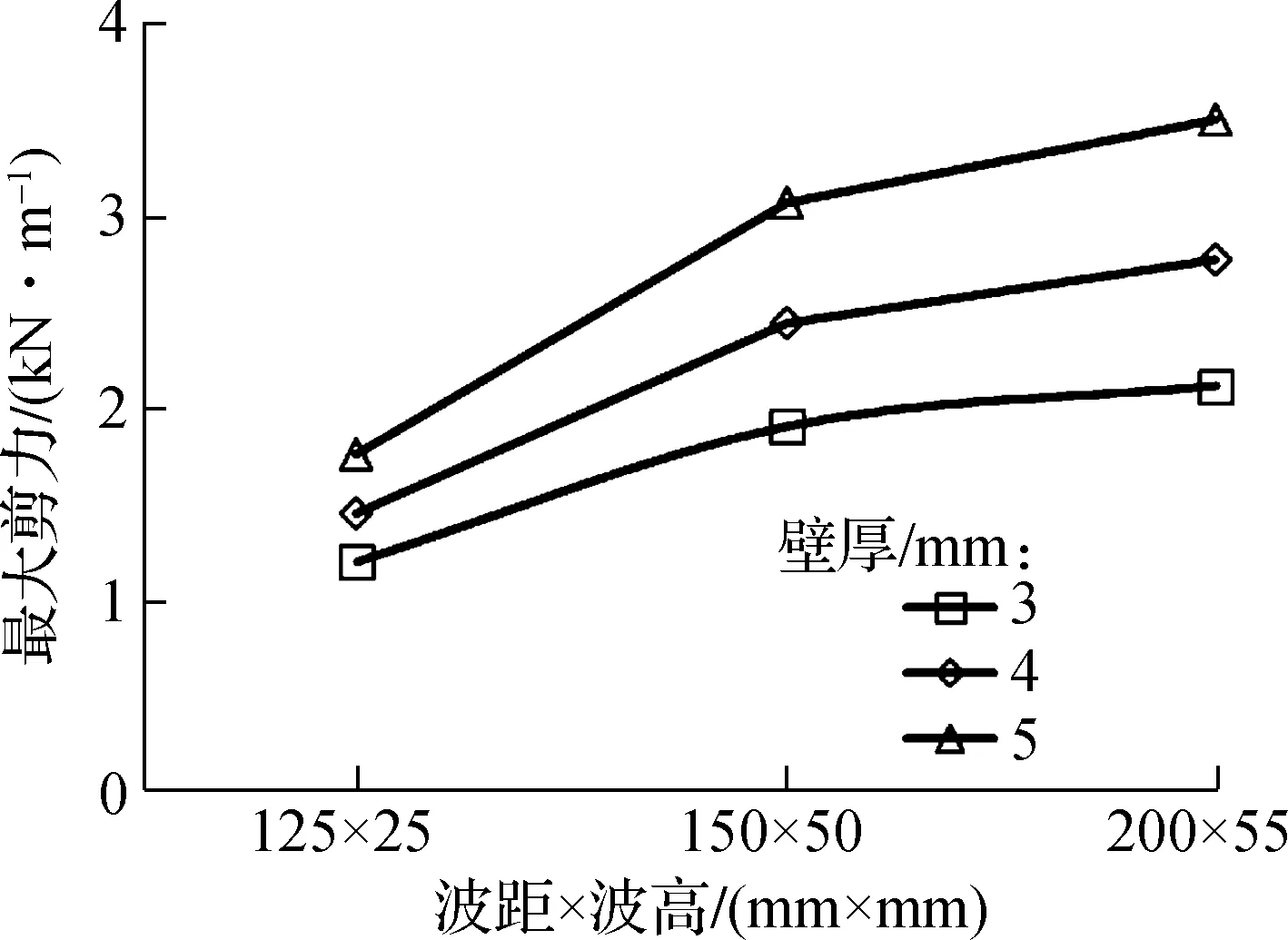
3.2.3 填土完成后壁厚与管道剪力的关系
管道填土结束后,壁厚对管道剪力的影响如图9所示(以工况P2为例).由图可见,壁厚对剪力影响很小;尽管P2对应的4 m直径的管道最大剪力与壁厚成线性增长关系,但浮动范围在1 kN/m左右,基本可忽略不计.
3.3 弯矩
3.3.1 填土过程中管道弯矩与填土高度的关系
填土过程中管道最大弯矩与填土高度的关系如图10所示(以工况P1为例).由图可见,最大弯矩仍随填土高度的增加而不断增大.对于壁厚为3 mm、波距×波高为150 mm×50 mm和200 mm×55 mm的钢波纹管,弯矩值相比于其他规格的钢波纹管更大,这是由于其刚度较大、变形较小导致的.这与剪力随填土高度的变化规律一致.
(a) 工况P1
(b) 工况P2
(c) 工况P3
(d) 工况P4
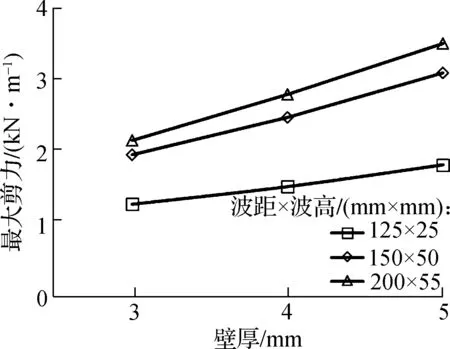
图9 填土完成后管道最大剪力与壁厚的关系(工况P2)
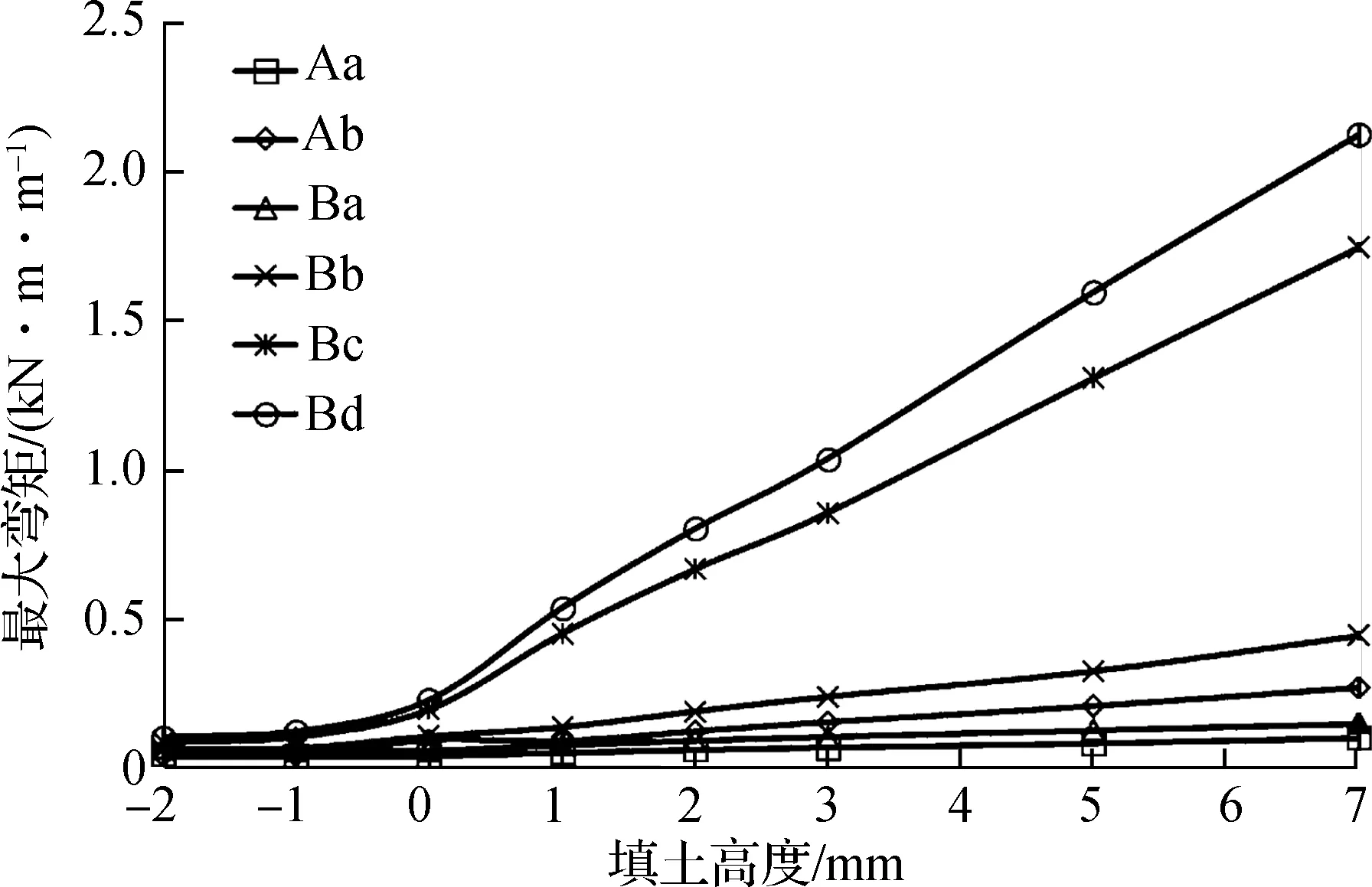
图10 填土过程中管道最大弯矩与填土高度的关系(工况P1)
3.3.2 填土完成后波距×波高与管道弯矩的关系
管道填土结束后,波距×波高对管道弯矩的影响如图11(a)所示(以工况P2为例).由图可见,填土结束后,管道的最大弯矩与波距×波高的关系同3.2.2节中剪力与波距×波高的关系一致,其根本原因为弯矩是剪力沿管周的积分.
3.3.3 填土完成后壁厚与管道弯矩的关系
管道填土结束后,壁厚对管道弯矩的影响如图11(b)所示(以工况P2为例).由图可见,填土结束后,工况P2对应的最大弯矩则随壁厚的增大均呈近似线性增长趋势.最大弯矩和剪力对应不同壁厚的变化规律相同.
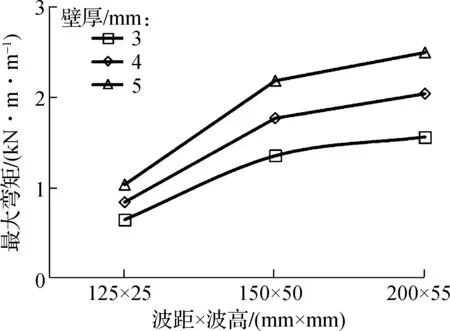
(a) 最大弯矩与波距×波高的关系
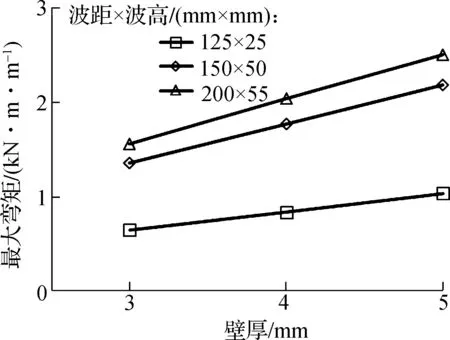
(b) 最大弯矩与壁厚的关系
4 现场验证分析
4.1 现场工况与数值模型的建立
管道施工现场位于江西,采用直径6.0 m的拼装钢波纹管,沟槽宽度为12.0 m.具体工况及利用波纹管截面计算法所得参数如表5所示.

表5 管道安装现场工况
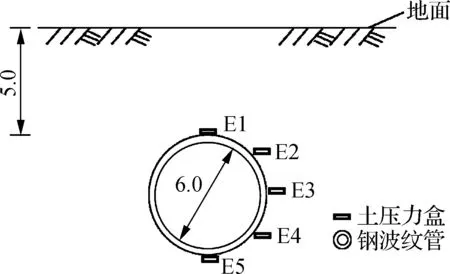
在管道施工现场管周布设土压力计和应变计以测量管周土体竖向土压力及管道环向应变.土压力计采用PCE0270型振弦式土压力计,量程为1.6 MPa,准确度为1.0% FS,分辨率为0.05% FS.应变计为RCE0350型振弦式应变计,量程为1 200×10-6(拉)和1 800×10-6(压),准确度为1.5% FS,分辨率为0.015% FS.采用数据采集器dataTaker设置1 s的步长记录管周竖向土压力和环向应变数据,土压力盒与应变计安装位置如图12所示.图12(a)中E1~E5为土压力盒;图12(b)中S1~S5为应变计.
管道施工现场的土体和管道的材料参数均与表3中一致.本研究中地下水位在沟槽以下,因此数值模型中不考虑地下水影响.为避免边界效应影响,模型尺寸设为50 m×35 m.
4.2 数据对比与分析
将数值模型分析结果及管道施工现场监测的管周土体竖向土压力及管道环向应变进行对比,结
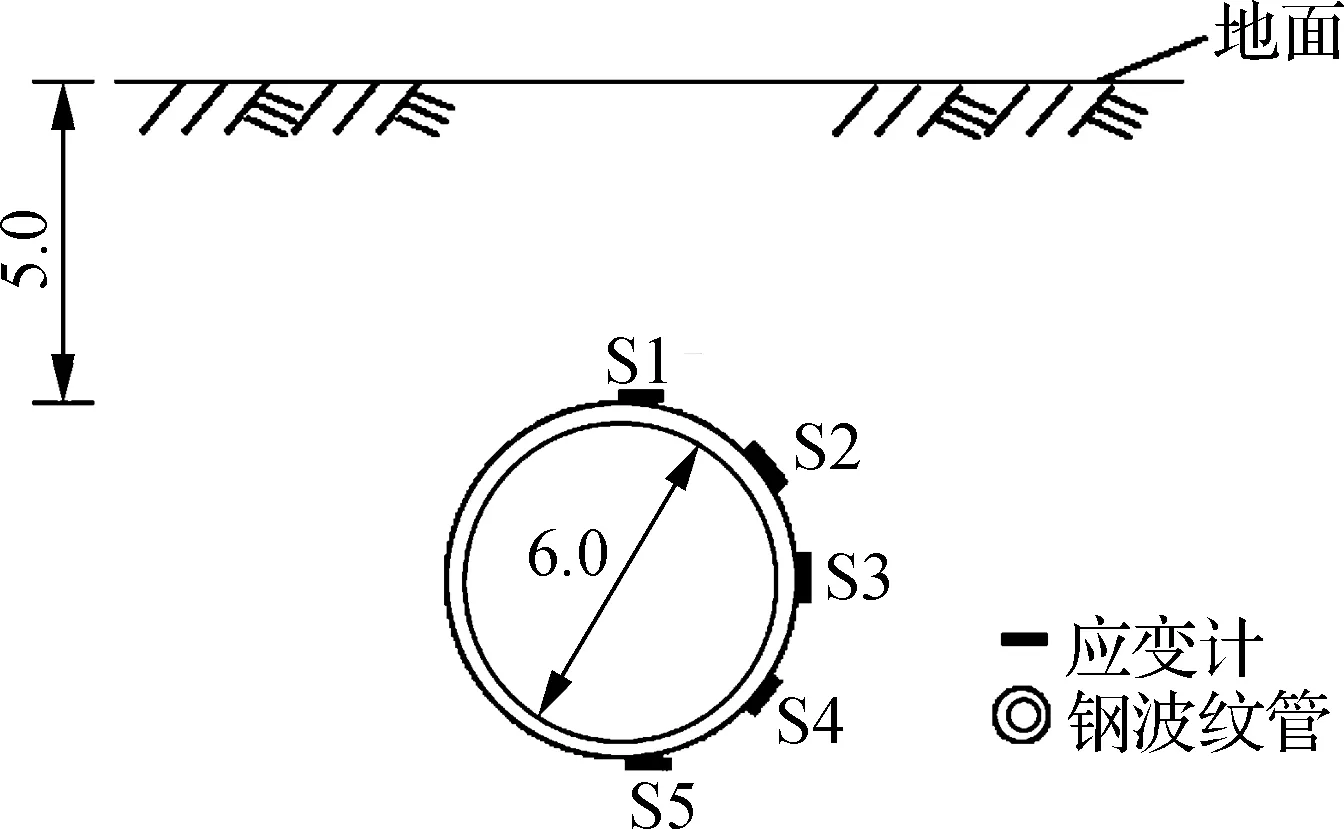
(b) 应变计安装位置
果如表6所示.由表6可知,数值模拟与实测数据误差较小,基本在10%以内.应变计S5处对应的误差普遍较高(9.75%~39.40%),这可能是由于该应变片在安装过程中受损.此外,现场监测读数存在机器误差,当土压力或应变的值较少时,误差较大(土压力误差最高达33.88%,为土压力盒E4在填土至管侧时的误差;管周应变误差最高达39.40%,为应变计S5在填土至管侧时的误差).
综合对比现场实测数据与数值模拟结果可知,本文所提出的方法可用于模拟现场管道施工过程中管土作用下钢波纹管的力学特性.
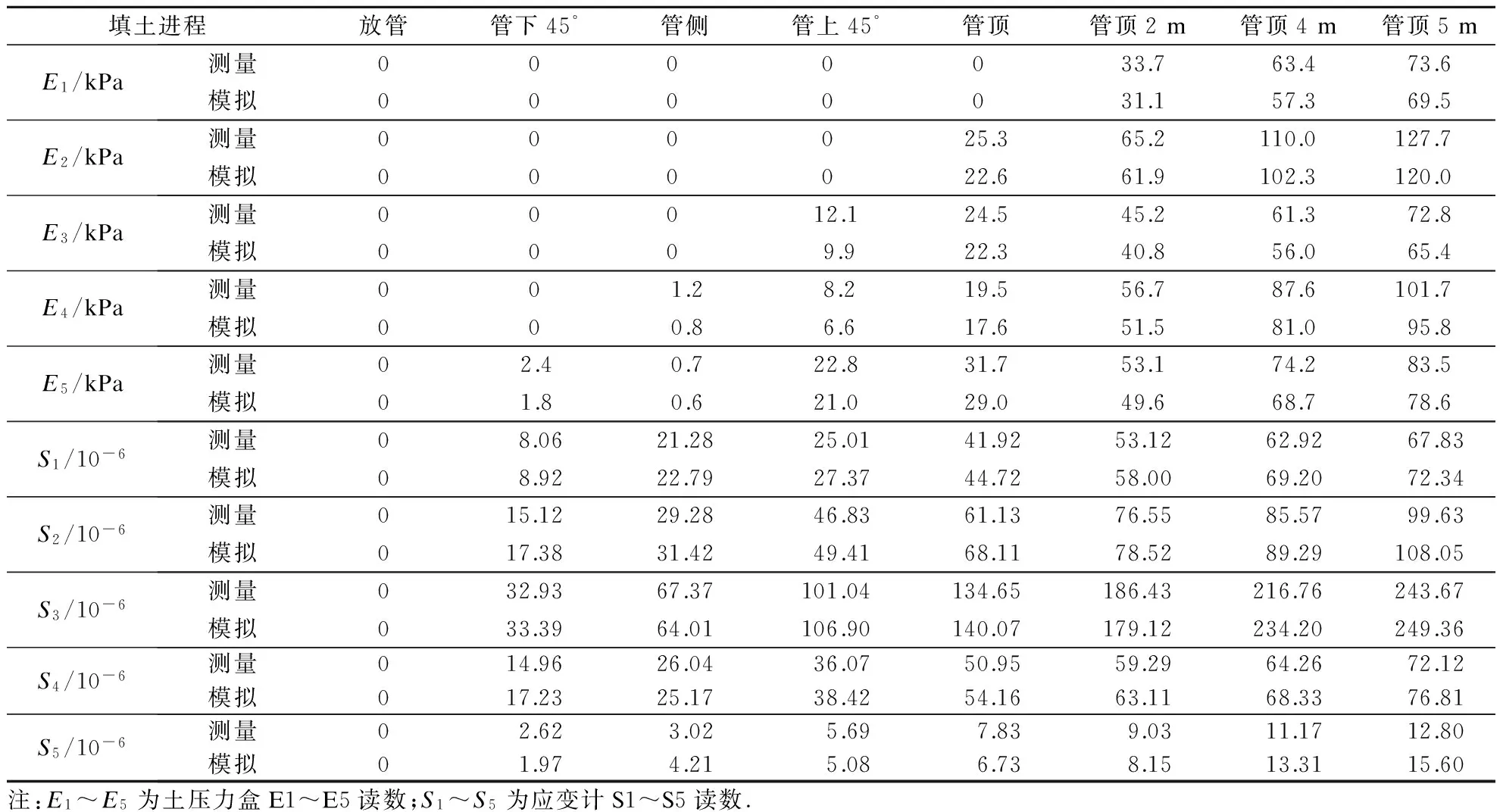
表6 现场实测与数值模拟对比
5 结论
1) 提出简便的截面参数分析法与有限元数值模拟相结合的方法对钢波纹管进行分析.将计算结果与美国钢波纹管规范(误差小于1.5%)和钢波纹管施工现场实测数据(误差基本小于10%)对比,证明该方法能准确反映钢波纹管道力学特性.
2) 放管时(特别是大直径管道)即能产生较大变形;填土过程中竖向变形大于其他方向变形;填土完成后管道的最大变形随着波距×波高的增加而减小,最后趋于稳定;设计时需设置一定的壁厚以满足波纹管的强度要求,但壁厚对其变形影响较小.
3) 根据波距×波高与壁厚对填土完成后的变形影响规律,得出适用平原地区及山地地区的2类工况中不同管径及填土高度的钢波纹管道最佳规格.
4) 钢波纹管道的内力(轴力、剪力、弯矩)均随着填土的进行逐渐增加.波距×波高较大的波纹管道相对于其他管道剪力与弯矩的增长速度更快.
5) 填土完成后,随着波距×波高和壁厚的增加,钢波纹管的最大轴力出现随之变大的趋势,但波距×波高比壁厚的作用更为明显;壁厚对钢波纹管最大剪力的影响较小;对直径较小的波纹管道,当波距×波高增大时,剪力会增大,管径较大时则规律相反;波距×波高和壁厚对填土完成后最大弯矩的影响与其对最大剪力的影响一致.
)
[1] 蒋雪梅,雷俊卿,王全录,等.波纹钢管涵洞的力学机理分析与试验研究[J].北京交通大学学报,2006,30(11):289-293.
Jiang Xuemei, Lei Junqing, Wang Quanlu, et al. Mechanical mechanism research of corrugated steel pipe culvert[J].JournalofBeijingJiaotongUniversity, 2006,30(11): 289-293. (in Chinese)
[2] 韩晓强.铁路钢波纹管涵洞的计算分析[J].工程建设与设计,2007(11):51-53. DOI:10.3969/j.issn.1007-9467.2007.11.016.
Han Xiaoqiang. Finite element analysis on railway corrugated steel culvert[J].Construction&DesignforProject, 2007(11): 51-53. DOI:10.3969/j.issn.1007-9467.2007.11.016.(in Chinese)
[3] 王艳丽,李祝龙,吴大中.钢波纹管涵洞的薄壳效应[J].公路交通科技,2008,25(5):86-90. DOI:10.3969/j.issn.1002-0268.2008.05.016.
Wang Yanli, Li Zhulong, Wu Dazhong. Thin shell effect of corrugated steel culvert performance[J].JournalofHighwayandTransportationResearchandDevelopment, 2008,25(5): 86-90. DOI:10.3969/j.issn.1002-0268.2008.05.016.(in Chinese)
[4] 粟缤.波纹管涵受力性能数值分析[D].北京:北京交通大学土木建筑工程学院,2009.
[5] Schroeder W L, Dickenson S E, Warrington D C.Soilinconstruction[M]. Park Carolina, India:Pearson Education India, 1975: 26-38.
[6] Albrecht M L. ASHS strategic planning and HortBase [J].HortTechnology, 1998,8(3): 316-317.
[7] Canadian Standards Association. Canadian highway bridge design code[S]. Toronto, Canada: Canadian Standards Association, 2006.
[8] American Society for Testing and Materials. A796—93 Standard practice for structural design of corrugated steel pipe. Pipe-arches, and arches for storm and sanitary sewers and other buried applications[S]. West Conshohocken, PA, USA: ASTM, 1999.
[9] 中华人民共和国交通运输部.JTG/TF50—2011公路桥涵施工技术规范[S].北京:人民交通出版社,2011.
[10] Corey R, Han J, Khatri D K, et al. Laboratory study on geosynthetic protection of buried steel-reinforced HDPE pipes from static loading[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2014,140(6): 04014019. DOI:10.1061/(asce)gt.1943-5606.0001113.
[11] 中华人民共和国交通运输部.JT/T710—2008公路桥涵波形钢板[S].北京:人民交通出版社,2008.
[12] 中华人民共和国交通运输部.JT/T791—2010公路涵洞通道用钢波纹管(板)[S].北京:人民交通出版社,2010.
[13] Sargand S, Masada T, Tarawneh B, et al. Deeply buried thermoplastic pipe field performance over five years[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2008,134(8): 1181-1191. DOI:10.1061/(asce)1090-0241(2008)134:8(1181).
[14] Carrier Ⅲ W D. Buckling versus deflection of buried flexible pipe[J].JournalofGeotechnicalandGeoenvironmentalEngineering, 2005,131(6): 804-807. DOI:10.1061/(asce)1090-0241(2005)131:6(804).
[15] Whidden W R.Buriedflexiblesteelpipe:Designandstructuralanalysis[M]. Virginia, USA: American Society of Civil Engineers, 2009: 28-29.
Analysisonmechanicalpropertyofcorrugatedsteelpipes
You Quan1Miao Linchang1Dong Dongdong2
(1Institute of Geotechnical Engineering, Southeast University, Nanjing 210096, China) (2Shanghai Municipal Engineering Design Institute (Group) Co., Ltd, Shanghai 200092, China)
A combined method of the sectional characteristic analysis and numerical simulation is proposed to analyze the mechanical and deformation properties of corrugated steel pipes. The analysis results were in agreement with ASTM specifications, which proved the effectiveness of the sectional characteristic analysis. By equivalently transforming corrugated pipes to solid wall pipes based on the sectional characteristic analysis results, a series of finite element models corresponding to different field conditions were established to investigate the deformation and internal force of corrugated steel pipes as well as the relationship between mechanical properties and specifications of pipes in the construction process. Also, recommended specifications of corrugated steel pipes were put forward. Finally, the results of the numerical model were compared with the measured vertical earth pressure around pipes and hoop strains of pipes in the field, demonstrating that the combined method is effective for corrugated pipe design. The proposed analysis method is convenient and can well reflect the mechanical properties of corrugated steel pipes.
corrugated steel pipe; equivalent method; mechanical property; field construction
10.3969/j.issn.1001-0505.2017.06.017
U175.2
A
1001-0505(2017)06-1187-08
2017-02-10.
尤佺(1992—),男,博士生;缪林昌(联系人),男,博士,教授,博士生导师,lc.miao@seu.edu.cn.
国家自然科学基金资助项目(51578147,51278099).
尤佺,缪林昌,董冬冬.钢波纹管的力学性能分析[J].东南大学学报(自然科学版),2017,47(6):1187-1194.
10.3969/j.issn.1001-0505.2017.06.017.

