基于张量线性拉普拉斯判别的肌电特征提取方法

佘青山 马鹏刚 马玉良 孟 明

(杭州电子科技大学智能控制与机器人研究所, 杭州 310018)

基于张量线性拉普拉斯判别的肌电特征提取方法

佘青山 马鹏刚 马玉良 孟 明

(杭州电子科技大学智能控制与机器人研究所, 杭州 310018)

为了有效分析表面肌电(sEMG)信号蕴含的时-频-空域多维特征,提出了一种基于张量线性拉普拉斯判别(TLLD)的sEMG特征提取方法.首先对sEMG信号做复Morlet小波变换,构造具有时间、空间、频率、任务的四阶张量数据;然后运用TLLD分析方法获得投影矩阵,把训练集和测试集分别投影在投影矩阵中获得具有较大区分度的特征;最后使用分类器对腕屈、腕伸、上臂内旋、上臂外旋、握拳、伸拳6种动作模式进行识别.实验结果表明, 所提方法平均分类准确率达到了98%以上,识别性能优于均方根、自回归系数、张量高阶判别分析3种特征提取方法.

表面肌电信号;人机交互;特征提取;张量线性拉普拉斯判别

基于生物电信号的新型人机交互已成为研究热点之一[1-2].其中,表面肌电(surface electromyogram, sEMG)蕴含丰富的信息,广泛应用于智能假肢、康复机器人等领域[3].

特征提取是基于sEMG信号的智能假肢控制系统的关键步骤之一,常用的方法包括时域、频域、时-频联合域、参数模型等方法[4].而上述大部分方法在数据处理过程中仅考虑了2个维度的信息(通道和时间),缺少同时考虑多维信息.张量分解(tensor decomposition, TD)方法能够有效地分析时域、频域、空域等多维信息[5],因此广泛应用在大数据分析[6]、图像渲染[7]、手写字体识别[8]、手势识别[9]、脑电信号识别[10-11]等领域.在TD方法中,投影矩阵的有效获得非常重要,常用方法包括高阶奇异值分解、高阶正交迭代、高阶判别分析(higher order discriminant analysis, HODA)等[12].目前,国内外学者采用TD方法对sEMG信号进行处理以及特征提取的研究较少.

传统的sEMG特征提取方法往往都是以向量为基础，并且使用欧式距离计算离散度矩阵,因此存在类间离散度矩阵奇异、投影方向有限等问题[13].针对上述问题,本文提出使用张量线性拉普拉斯判别(tensor linear laplacian discriminant, TLLD)分析方法,从sEMG信号的张量数据中提取特征,寻找最佳的投影矩阵，以获取特征.TLLD方法在权重选择上借鉴了线性拉普拉斯判别(linear laplacian discriminant, LLP)算法的优点,但是在距离度量选择上采用新颖的语境距离度量[14].首先采集人体上肢进行腕屈、腕伸、上臂内旋、上臂外旋、握拳、伸拳等6个动作模式下所涉及的几组肌肉处的sEMG信号,其次采用复Morlet小波变换构建具有时间、空间、频率、任务的张量数据.然后采用TLLD方法寻找最佳投影矩阵以获得具有较大区分度的张量高维特征,接着对高维张量特征进行矩阵化和降维.最后采用分类器对降维后的特征进行分类.与当前几种sEMG特征提取方法进行比较分析,实验结果验证了该方法的有效性.

1 张量表述

根据张量的定义[15],多通道的sEMG信号表示为一个n阶张量X,经过投影后得到一个低维张量Y，即

Y=X×1A(1)×2A(2)…×nA(n)

(1)

2 基于TLLD的特征提取方法

2.1 sEMG数据的张量表示

为了同时考虑sEMG信号的时-频-空域等多维信息,本文采用张量分解方法对其进行特征提取.目前,构造张量数据的方法包括短时傅里叶变换、小波变换等.复Morlet小波在时域和频域上有良好的分辨率,被广泛应用于生物电信号的数据处理中[16],因此本文采用复Morlet小波分析方法建立张量.

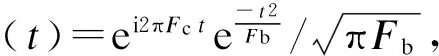
(2)

式中,Fc为中心频率;Fb为带宽参数.实验数据经过复Morlet小波变换可以建立描述肌电信号中多维信息的张量结构.具体而言,本文建立了一个4阶张量,分别表示空间、频率、时间、任务等多维度上的信息.在实验中,sEMG数据具有通道×时间×任务三维结构,经过复Morlet小波变换后构建的张量数据具有通道×频率×时间×任务四维结构,记为A.

2.2 TLLD获取投影矩阵

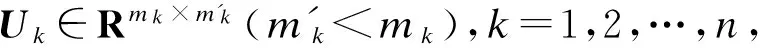
(3)

式中,Yi具有最小的类内方差和最大的类间方差.

按照LLD方法,定义如下类内离散度:

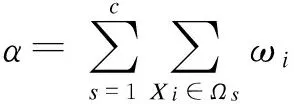
(4)

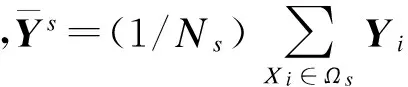
(5)

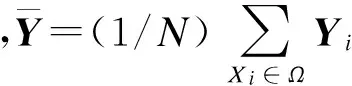
TLLD方法旨在寻找投影正交矩阵Uk,同时要求最小化α和最大化β,希望使得投影后的样本尽可能离散,各个样本内部又尽可能聚集.该优化目标可以用Fisher准则函数来表示，即

(6)

式中,Ui(i=1,2,…,n)很难同时求出,本文采用迭代算法进行求解.根据文献[17],对基于矩阵的降维方法进行扩展,在张量中重新定义α和β,并且进行k阶展开:

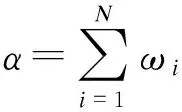
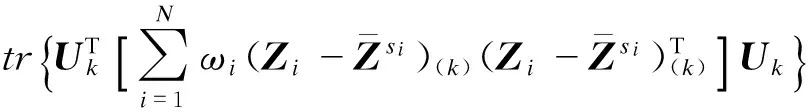
(7)

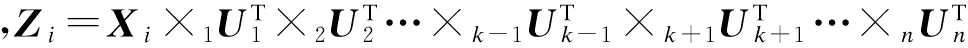
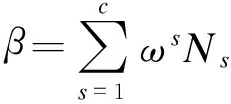
(8)

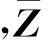
(9)

(10)

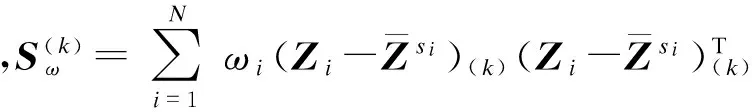
(11)

2.3 特征生成和选择

计算出投影矩阵Uk(k=1,2,…,n)后,本文将构建好的高阶训练集张量Atr和测试集张量Ats分别投影到共同的投影矩阵中,得到如下的张量特征:

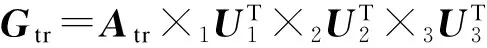
(12)

式中,Gtr和Gts分别为训练集和测试集的张量特征，由于其还具有张量结构,还要对其进行矩阵化．但矩阵化后特征维数仍然较大,包含了较多的冗余信息,因此需要进一步降维．本文采用常规的Fisher分数方法对高维的张量特征进行降维处理,根据最佳平均分类准确率确定最终的特征维数.

3 实验过程与结果分析

3.1 实验过程

为了证明本文方法的有效性,采集了表面肌电信号进行实验与分析.选取了5名身体状况良好的男性作为实验对象(S1～S5),均为右利手,年龄为(23.4±0.5)岁.采集设备为Delsys Trigno无线表面肌电系统,采样频率为2 kHz.根据参考文献[21],在前臂靠近肘关节处选择沿与肌肉纤维平行方向的手臂上均匀安放8个表面肌电电极.受试者实验前没有进行剧烈运动,舒适地坐在实验平台前面,肘关节以自然放松的状态直立放在实验平台支撑面上.按照要求完成腕屈、腕伸、上臂外旋、上臂内旋、握拳、展拳等6种动作,如图1所示.每个动作持续时间为4 s,重复进行30次,每次实验过程中都设置休息放松时间,防止肌肉疲劳.

(c) 前臂内旋 (d) 前臂外旋

(e) 握拳 (f) 展拳

3.2 参数选取

在sEMG数据的张量表示中,本文采用交叉验证方法来选取中心频率Fc、带宽参数Fb等.根据文献[12]中脑电信号的参数选择,并经过大量实验验证后,设置Fc=1,Fb在1～6范围内进行选取.每名受试经过10次5折交叉验证所得的识别结果如图2所示.由图可以看出,当中心频率为1时,随着Fb的取值从1增加6,分类正确率并不呈现单调递增的趋势．5名受试者在Fb为2～4之间均取得较高的正确率,当Fb=3时平均正确率最高.考虑算法对不同受试者的适应性,本文选取Fb=3.

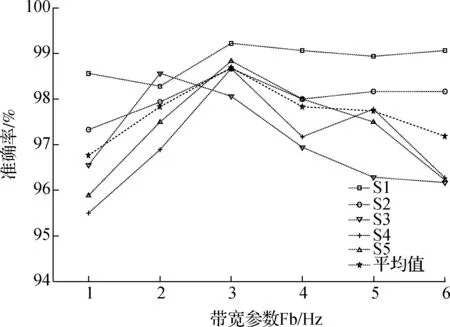
图2 不同带宽参数下的识别率比较

3.3 结果分析

以受试者S1实验数据为例, sEMG原始数据为8×8 000×180(通道×时间×任务),经过复Morlet小波变换后成为四阶张量,即8×34×100×180(通道×频率×时间×任务).经过TLLD方法获得的3个投影矩阵分别为U8×4,U34×17,U100×32,数据投影和矩阵化后,每一个任务的特征维数为T=4×17×32=2 176,而原始数据对应的特征维数为T=8×8 000=64 000.虽然相较于原始数据,张量特征的维数已在很大程度上得以降低,但是维数依然较高.因此还需要对特征数据进行降维,进一步去除冗余信息,以获得具有较好区别度的特征.本文采用Fisher分数方法选择特征,并使用LDA进行分类.不同特征维数下,统计5名受试者进行10次5折交叉验证，得到的平均分类准确率,如图3所示.由图可以看出,随着特征维数的增加,平均正确率呈现出增长的趋势,当特征维数为13时,正确率达到最大值,但随着特征维数的增加，正确率并没有继续增加因此,本文选择特征维数为13.

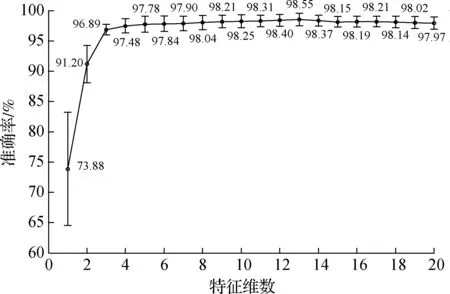
图3 不同特征维数下的分类准确率比较

为了证明本文方法的有效性,将其与时域、参数模型和张量分解的特征提取方法(包括均方根RMS[22]、AR参数法[23]和高阶判别分析HODA[12])进行比较.首先分别采用上述4种方法对5名受试者的sEMG数据进行特征提取,然后采用LDA方法进行分类,经过10次5折交叉验证后的平均正确率如图4所示.

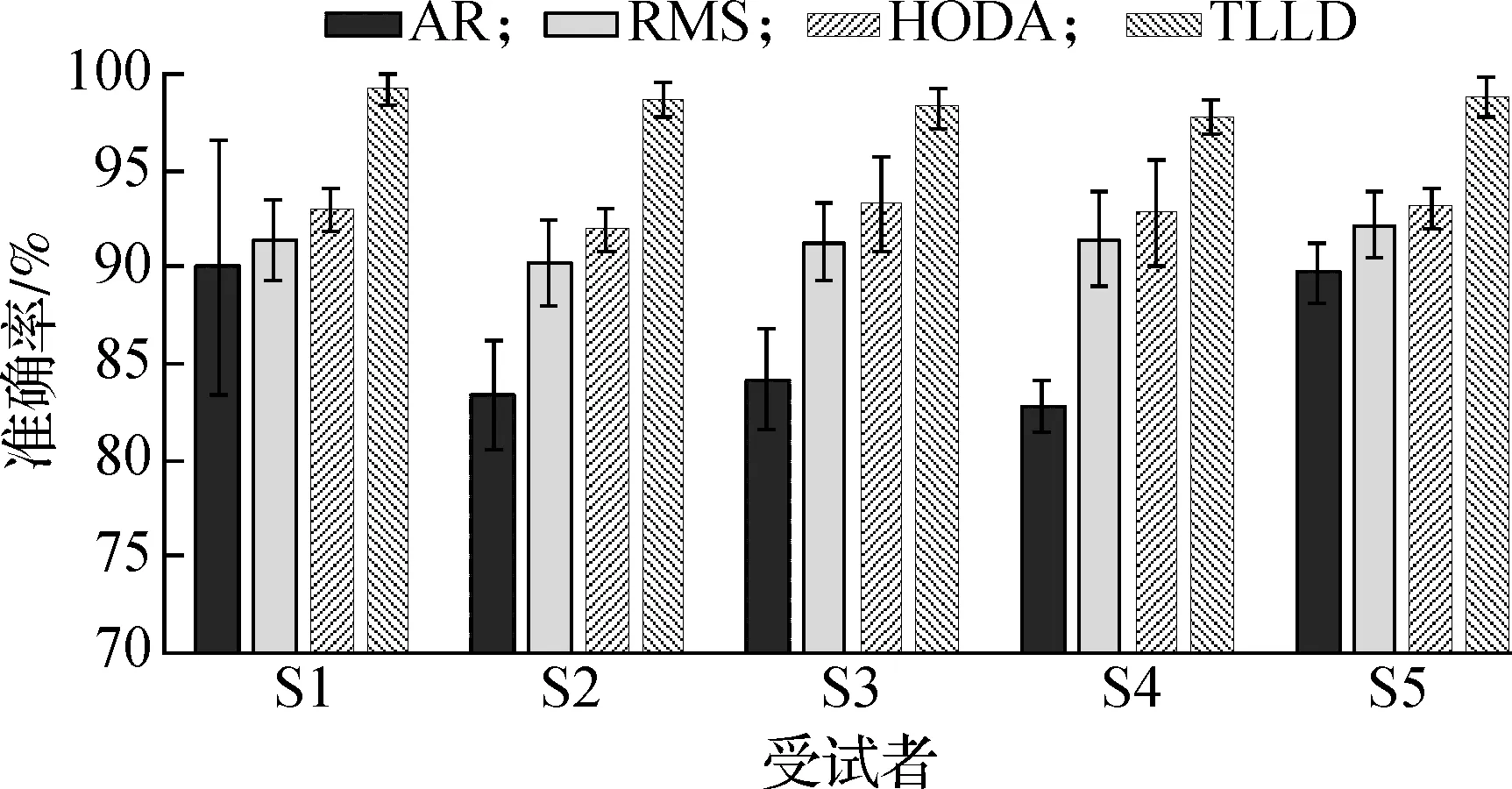
图4 六类动作识别正确率

对于5位受试者而言,2种基于张量表示的特征提取方法HODA和TLLD具有明显的优势,高于其他2种方法.动作识别正确率HODA方法高于AR方法6.84%,高于RMS方法1.62%,本文方法高于HODA方法5.73%,达到了98.57%.从整体来看,传统的2种特征提取方法存在个体差异性,不同的受试者在分类正确率上有较大的波动性,而本文方法能够准确地识别出6种动作,体现了其在sEMG特征提取上的有效性.

除了不同特征提取方法的性能比较外,还采用不同的分类方法进行了实验．针对本文方法提取出的肌电特征,分别使用线性分类器、支持向量机(supported vector machine, SVM)和最近邻法(K-nearest neighbours, KNN)进行识别,10次5折交叉验证的平均准确率比较结果如图5所示.可以看出,3种分类方法均有较高的识别正确率,平均正确率均在98%以上,且SVM分类结果最好,LDA和KNN分类方法正确率大致相同,说明了所提方法在sEMG特征提取上的优越性.

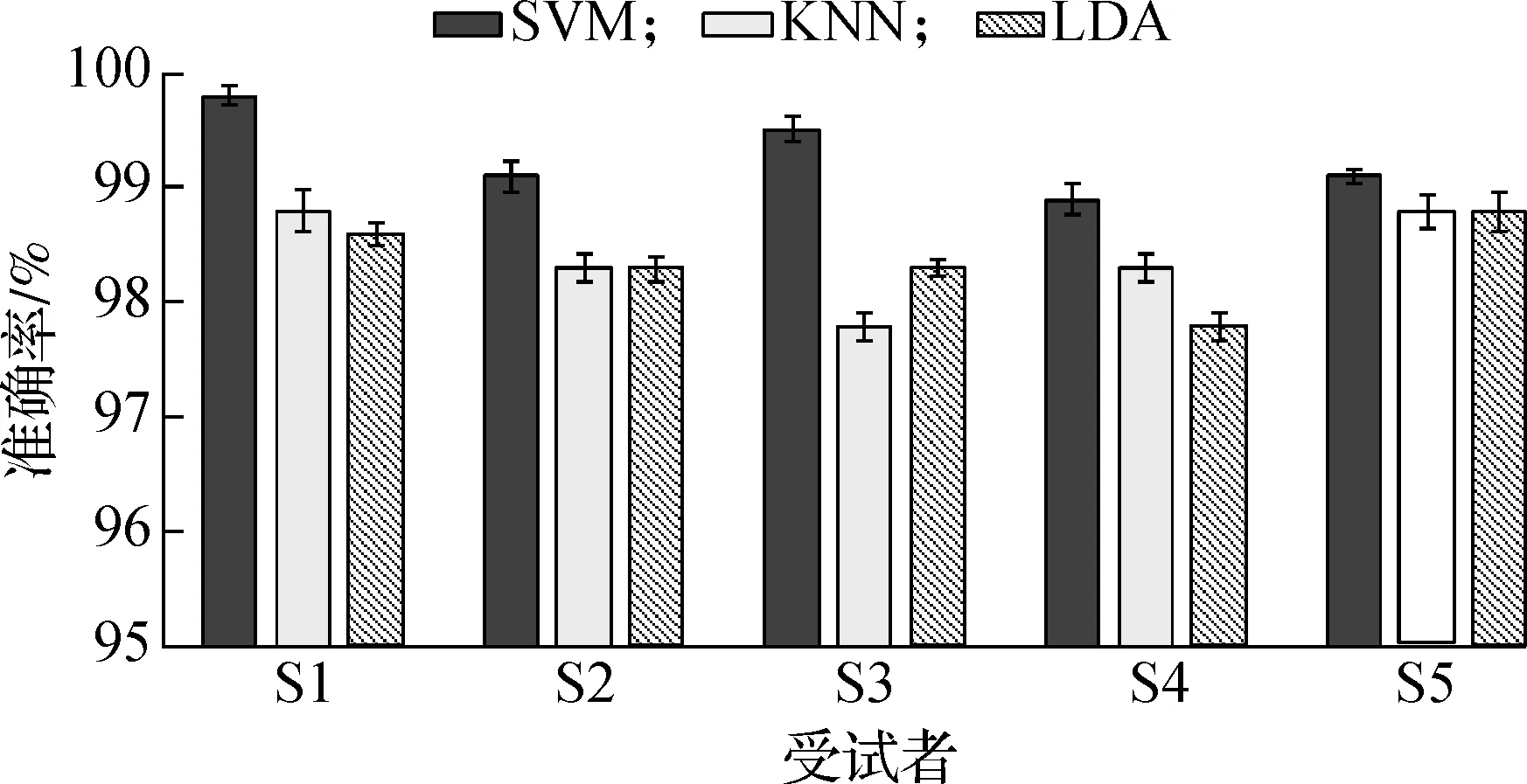
图5 不同分类方法的性能比较

4 结语

本文将张量结构应用于肌电信号处理中,通过时间、空间、频率、任务等多模式张量来表征sEMG信号,提出了一种联合域的肌电特征提取方法.首先使用复Morlet小波变换构建sEMG信号的张量数据.其次采用TLLD方法寻找最佳投影矩阵以获得具有较大区分度的张量特征,然后对张量特征进行矩阵化,并采用Fisher分数法对高维的张量特征进行降维.最后采用分类器对降维后的特征进行分类．实验结果表明,与均方根、AR参数法和高阶判别分析等特征提取方法相比,本文方法有效地改善了分类效果,为肌电信号特征提取提供了一种新的思路.

)

[1] 侯增广, 赵新刚, 程龙, 等.康复机器人与智能辅助系统的研究进展[J]. 自动化学报, 2016, 42(12): 1765-1779. DOI:10.16383/jaas2016y000006.

Hou Zengguang, Zhao Xingang, Cheng Long, et al. Recent advances in rehabil-itation robots and intelligent assistance systems[J].ActaAutomaticaSinica, 2016,42(12): 1765-1779.DOI:10.16383/jaas2016y000006. (in Chinese)

[2] 丁其川, 熊安斌, 赵新刚, 等.基于表面肌电的运动意图识别方法研究及应用综述[J]. 自动化学报, 2016, 42(1): 13-25.DOI:10.16383/jaas2016c140563.

Ding Qichuan, Xiong Anbin, Zhao Xingang, et al. A review on researches and applications of sEMG-based motion intent recognition methods[J].ActaAutomaticaSinica, 2016,42(1): 13-25.DOI:10.16383/jaas2016c140563. (in Chinese)

[3] 王涛, 侯文生, 吴小鹰,等.用于肌电假肢手控制的表面肌电双线性模型分析[J]. 仪器仪表学报, 2014, 35(8): 1907-1913.

Wang Tao,Hou Wensheng,Wu Xiaoying, et al. Analysis of the sEMG bilinear model for the control of hand prosthesis[J].ChineseJournalofScientificInstrument, 2014,35(8): 1907-1913. (in Chinese)

[4] 刘建, 邹任玲, 张东衡, 等.表面肌电信号特征提取方法研究发展趋势[J]. 生物医学工程学进展, 2015, 36 (3): 164-168. DOI:10.3969/jissn1674-1242.2015.02.009.

Liu Jian,Zou Renling,Zhang Dongheng, et al. Research and development trend of feature extraction methods of surface electromyogrphic signals [J].ProgressinBiomedicalEngineering, 2015,36(3): 164-168. DOI:10.3969/jissn1674-1242.2015.02.009. (in Chinese)

[5] Vervliet N, Debals O, Sorber L, et al. Breaking the curse of dimensionality using decompositions of incomplete tensors: Tensor-based scientific computing in big data analysis [J].IEEESignalProcessingMagazine, 2014,31(5): 71-79. DOI:10.1109/MSP2014.2329429.

[6] Papalexakis E E, Faloutsos C, Sidiropoulos N D. Tensors for data mining and data fusion: Models, applications, and scalable algorithms [J].ACMTransactionsonIntelligentSystemsandTechnology, 2016,8(2): 16-1-16-44. DOI: http://dxdoiorg/10.1145/2915921.

[7] Vasilescu M A O, Terzopoulos D. TensorTextures: Multilinear image-based rendering [J].ACMTransactionsonGraphics, 2004,23(3): 336-342. DOI: 10.1145/1186562.1015725.

[8] Savas B, Elden L. Handwritten digit classification using higher order singular value decomposition [J].PatternRecognition, 2007,40(3): 993-1003. DOI: 10.1016/jpatcog2006.08.004.

[9] Zhang J, Xu C, Jing P, et al. A tensor-driven temporal correlation model for video sequence classification[J].IEEESignalProcessingLetters, 2016,23(9): 1246-1249. DOI: 10.1109/LSP2016.2577601.

[10] Phan A H, Cichocki A, Vu-Dinh T. A tensorial approach to single trial recognition for brain computer interface [C]//ProceedingsofIEEEInternationalConferenceonAdvancedTechnologiesforCommunications. Ho Chi Minh City, Vietnam, 2010: 138-141. DOI: 10.1109/ATC2010.5672697.

[11] Li L, Boulware D. High-order tensor decomposition for large-scale data analysis [C]//ProceedingsofIEEEInternationalCongressonBigData. New York, USA, 2015: 665-668. DOI: 10.1109/BigdDataCongress2015.104.

[12] Phan A H, Cichocki A. Tensor decompositions for feature extraction and classification of high dimensional datasets [J].NonlinearTheoryandItsApplications, 2010,1(1): 37-68. DOI: 10.1587/nolta1.37.

[13] Zhang W, Lin Z, Tang X. Tensor linear Laplacian discrimination (TLLD) for feature extraction [J].PatternRecognition, 2009,42(9): 1941-1948.DOI: 10.1016/jpatcog2009.01.010.

[14] 皋军, 王士同, 王晓明，等.基于语境距离度量的拉普拉斯最大间距判别准则[J]. 自动化学报, 2010, 36(12): 1661-1673.DOI 10.3724/SPJ1004.2010.01661.

Gao Jun, Wang Shitong, Wang Xiaoming, et al. Contextual-distance metric based laplacian maximum margin criterion [J].ActaAutomaticaSinica, 2010,36(12): 1661-1673. DOI 10.3724/SPJ1004.2010.01661. (in Chinese)

[15] de Lathauwer L, de Moor B, Vandewalle J. A multilinear singular value decomposition [J].SiamJournalonMatrixAnalysis&Applications, 2000,21(4): 1253-1278.DOI: 10.1137/S0895479896305696.

[16] Xie P, Song Y. Multi-domain feature extraction from surface EMG signals using nonnegative tensor factorization [C]//ProceedingsofIEEEInternationalConferenceonBioinformaticsandBiomedicine. Shanghai, China, 2013: 322-325. DOI: 10.1109/bibm2013.6732510.

[17] He X, Cai D, Liu H, et al. Image clustering with tensor representation [C]//ProceedingsofACMInternationalConferenceonMultimedia. Singapore, 2005: 132-140.DOI: 10.1145/1101149.1101169.

[18] Wang H, Yan S, Xu D, et al. Trace ratio vs ratio trace for dimensionality reduction [C]//ProceedingsofIEEEConferenceonComputerVisionandPatternRecognition. Minneapolis, MN, USA, 2007: 1-8. DOI: 10.1109/CVPR2007.382983.

[19] He X, Cai D, Niyogi P. Tensor subspace analysis [J].AdvancesinNeuralInformationProcessingSystems, 2005: 499-506. DOI:10.1016/0031-3203(94)00135-9.

[20] Li X, Lin S, Yan S, et al. Discriminant locally linear embedding with high-order tensor data [J].IEEETransactionsonSystemsManandCybernetics-PartB:Cybernetics, 2008,38(2): 342-352. DOI:10.1109/TSMCB2007.911536.

[21] Jiang N, Englehart K B, Parker P A. Extracting simultaneous and proportional neural control information for multiple-DOF prostheses from the surface electromyographic signal [J].IEEETransactionsonBiomedicalEngineering, 2009,56(4): 1070-1080. DOI:10.1109/TBME2008.2007967.

[22] Naik G R, Nguyen H T. Nonnegative matrix factorization for the identification of EMG finger movements: Evaluation using matrix analysis [J].IEEEJournalofBiomedical&HealthInformatics, 2015,19(2): 478-485. DOI: 10.1109/JBHI2014.2326660.

[23] 罗志增, 杨广映.表面肌电信号的AR参数模型分析方法[J]. 传感技术学报, 2003, 16(4): 384-387.DOI: 10.3969/jissn1004-1699.2003.04.002.

Luo Zhizeng, Yang Guangying. Surface electromyography analytical method based on the parameter of AR model [J].ChineseJournalofSensorsandActuators, 2003,16(4): 384-387.DOI: 10.3969/jissn1004-1699.2003.04.002.(in Chinese)

EMGfeatureextractionbasedontensorlinearLaplaciandiscriminant

She Qingshan Ma Penggang Ma Yuliang Meng Ming

(Institute of Intelligent Control and Robotics, Hangzhou Dianzi University, Hangzhou 310018, China)

To analyze the multi-dimensional characteristics in the time-frequency-space domain implied in the surface electromyogram (sEMG) signlas, a novel feature extraction method for sEMG was proposed based on tensor linear Laplacian discriminant (TLLD) First, sEMG signals were transformed into the 4-D tensor data including the information of temporal, spatial, spectral, and trials by complex morlet wavelet. Secondly, the TLLD analysis algorithm was used to obtain the projection matrix, and the training and test sets were projected into the projection matrix to obtain features with greater discrimination. Finally, the linear discriminant analysis algorithm was used to identify six forearm movements, including the wrist flexion, wrist extension, forearm pronation, forearm supination, hand close, and hand open. The experimental results show that the accuracy of the proposed method is more than 98%, and its recognition performance is better than that of three methods of the root mean square, autoregressive coefficient and tensor high order discriminant analysis.

surface electromyogram; human-robot interaction; feature extraction; tensor linear Laplacian discriminant

10.3969/j.issn.1001-0505.2017.06.006

TP391

A

1001-0505(2017)06-1117-06

2017-06-17.

佘青山(1980—),男,博士,副教授, qsshe@hdu.edu.cn．

国家自然科学基金资助项目(61201302, 61372023, 61671197)、浙江省自然科学基金资助项目(LY15F010009).

佘青山,马鹏刚,马玉良,等.基于张量线性拉普拉斯判别的肌电特征提取方法[J].东南大学学报(自然科学版),2017,47(6):1117-1122.

10.3969/j.issn.1001-0505.2017.06.006.